[CS224W] Lecture 3 - Node Embeddings

김재희·2021년 7월 29일

CS224W

목록 보기

3/11

0. Traditional ML for Graphs

노드 임베딩을 다루기 전에, 이전의 머신러닝 기법이 어떻게 그래프를 다뤘는지 다시 한번 생각해보자.

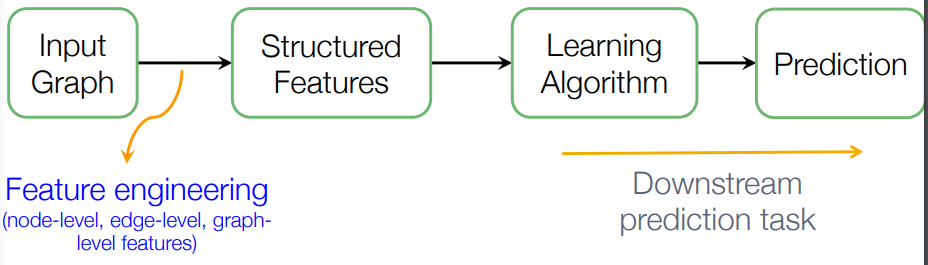
머신러닝 기법들은 그래프를 각각의 도메인과 태스크에 맞게 feature engineering하여 노드, 링크, 그래프 레벨의 변수들을 생성했다. 그리고 이렇게 만들어진 변수를 이용해 또다시 각각의 태스크와 도메인에 맞게 모델을 정하고, 튜닝하여 예측하였다.

하지만 이렇게 진행되다 보니, 각 태스크와 도메인마다 새로 feature engineering이 진행되어야 했다. 앞에서 잠깐 배웠듯이, 그 과정은 간단하지도, 시간이 적게 들지도 않는다. 그래서 이제는 representation learning을 통해 우리가 배울 모델들이 적절하게 변수들을 뽑아낼 수 있도록 학습시킬 것이다.

1. Graph Representation Learning

그래프 표상 학습은 결국 그래프의 요소(노드, 링크, 그래프)를 입력으로 하여 임의의 d차원 벡터로 변환시키는 작업이다. 그 과정에서 모델이 사용되며, 해당 모델은 그래프의 요소를 임베딩 공간으로 맵핑시키게 된다.

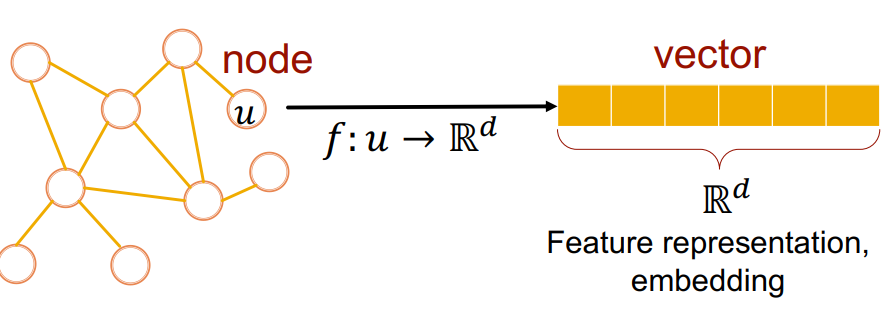
즉, 토큰이라는 discrete한 변수를 임베딩 공간으로 맵핑시키듯이, 이번 수업에서는 각 노드들을 유사도를 기준으로 임베딩 공간에 맵핑시켜 비슷한 노드는 임베딩 공간 내에 근처에서 위치하도록 만드는 작업이다.

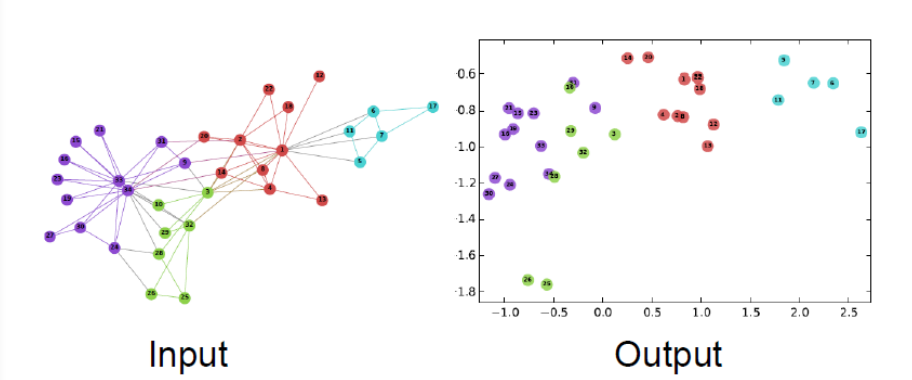
위 그림은 아주 간단한 예시를 보여주고 있는데, input으로 그래프를 받아서, 2차원 임베딩 공간에 맵핑한 모습이다. 한눈에 봐도 그래프에서의 노드들의 관계가 2차원 공간에 잘 보여지고 있는 모습이다.

2. Node Embedding Basic

노드 임베딩을 위해 기본적인 요소들을 짚고 넘어가자.
우선 V는 노드 집합이고, A는 인접행렬을 의미한다.

그리고 노드 임베딩이란 아래 그림의 과정을 의미한다.

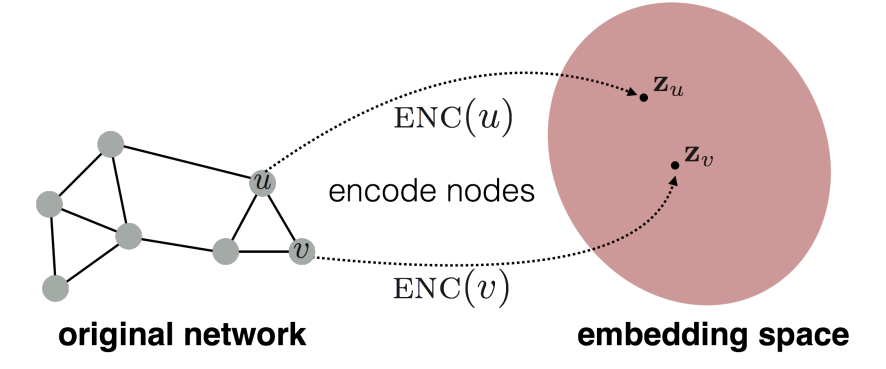
입력값으로 주어지는 그래프의 각 노드가 임의의 인코더를 통과하여 임베딩 공간에 위치하는 벡터로 바뀌는 과정이다.
그리고 이 과정은 그래프에서 유사한 노드들이 임베딩 공간에서도 근처에 있도록 맵핑하고자 하는 것이다.

수식으로 목적을 표현하면 다음과 같을 것이다.

z_u = Enc(u)\\ z_v = Enc(v)\\ similarity(u, v) \approx z_v^Tz_u

그래프에서 두 노드 u, v의 유사도는 임베딩 공간에서의 두 벡터 $z_u, z_v$ 의 유사도로 근사되어야 한다. (여기서 임베딩 공간의 유사도로 내적을 사용했다.)

아직 우리가 모르는 것은 다음과 같다.
1. 어떻게 그래프에서 유사도를 정의할지.
2. 어떻게 인코더를 구성할지.

2-1. Framework

전반적인 노드 임베딩의 과정은 다음과 같다.
1. 인코더가 노드를 임베딩 공간으로 맵핑하여 벡터를 생성한다.
2. 노드 유사도 함수를 정의하고, 이를 통해 그래프에서 노드 간 유사도를 측정한다.
3. 디코더가 맵핑된 벡터에 대해 유사도를 측정한다.
4. 2와 3에서 측정된 유사도가 비슷해지도록 인코더의 파라미터를 최적화한다

2-1-1.Shallow Encoding

가장 단순한 인코딩 방식은 인코더가 단순히 embedding-lookup하는 것이다.
embedding-lookup이란 룩업 테이블에서 입력으로 주어진 인덱스의 열만 출력하는 것을 의미한다.

\textbf{Z} \in \mathbb{R}^{d \times \vert \mathcal{V} \vert}\\ \mathcal{v} \in \mathbb{I}^{\vert \mathcal{V} \vert}

즉 인코더는 그림의 왼쪽과 같아 dxV 룩업 테이블 Z을 가지고 있고, 입력값으로 임베딩하는 노드의 인덱스만 1인 one hot vector를 받는다. 그러면 룩업 테이블과 벡터를 곱하여 해당 노드의 임베딩 벡터를 출력하게 되는 것이다. 이때, 최적화하고자 하는 파라미터는 Z에 있는 각 노드의 임베딩 벡터이다.

가장 간단한 방법으로 각각의 노드가 개별적인 임베딩 벡터를 가지고 있게 되는 것이다. 하지만 이는 노드 수가 많아지게 될 경우 가지고 있어야 하는 룩업 테이블이 무척 커지게 되는 단점이 있다고 한다.

다시한번 노드 임베딩에서 인코더가 최적화되는 목적함수를 짚고 넘어가자.

유사한 노드 쌍 (u, v)을 임베딩한 벡터의 내적 $z^T_Vz_U$ 를 최대화하는 것.

2-1-2. Node Similarity

그렇다면 그래프에서 노드 유사도를 정의할 수 있을까? 연결의 유무, 이웃 노드의 공유 여부, 구조적 특징의 유사도를 이용해야 할까?

이번 시간에는 random walks를 이용해 노드의 유사도를 정의하고자 한다.
노드 임베딩 자체는 비지도 학습 혹은 자기지도 학습의 일종으로 노드의 레이블이나 변수들을 전혀 사용하지 않는다. 대신 그래프의 구조를 보존하면서 직접적으로 노드들의 좌표계를 얻고자 한다. 이를 통해 태스크 마다 개별적으로 임베딩할 필요없이 하나의 임베딩을 다양한 태스크에 사용할 수 있다.

3. Deepwalk

3-1. Notation

Vector $z_u$ : 노드 u의 임베딩 벡터
Probability $P(v \vert \textbf{z}_u) : 노드 u에서 출발하여 랜덤워크하여 노드 v에 도착할 확률 추정치
Softmax : $\sigma(\textbf{z}_i) = {e^{z_i} \over \sum_{j = 1}^K e^{z_j}}$
Sigmoid : S(x) = ${1 \over 1 + e^{-x}}$

3-2. 랜덤워크란?

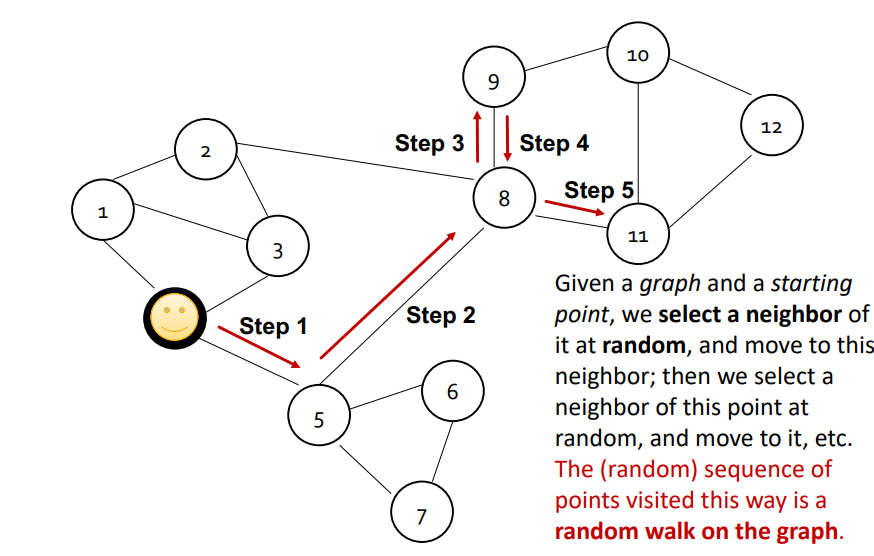
위 그림과 같이 그래프가 주어지고 특정 노드에서 시작하여 한번에 하나씩 이웃 노드로 랜덤하게 옮겨간다고 할 때, 연속적으로 옮겨가는 노드 시퀀스를 랜덤워크라고 한다. 또한 옮기는 횟수는 고정되거나 특정 전략을 통해 이뤄지는데 이를 R로 표기합니다. 즉, 출발 노드에서 움직이면서 그 기록을 남긴 것을 랜덤워크라고 합니다. 위의 랜덤워크는 [5, 8, 9, 8 ,11]이 될 것입니다.

그래프에서 각 노드에 대해 랜덤워크를 기록하게 되면, 총 V개의 랜덤워크가 있게 됩니다. 만약 노드 u와 노드 v가 전체 랜덤워크에서 같이 등장하는 확률이 높다면, 두 노드는 서로 가까이 있다는 의미가 될 것 입니다. 두 노드 사이에 엣지가 많거나 경로가 짧아서 자주 같이 등장한 것이기 때문입니다. 이러면 랜덤워크를 이용해 그래프에서 두 노드 (u, v)의 유사도를 측정할 수 있게 된 것이라고 할 수 있을 것입니다. 이전에 그래프에서 근처에 있는 노드를 유사도가 높다고 생각하자고 했고, 근처에 있는 노드면 확률이 높을 것이기 때문입니다.

그래프에서의 두 노드 (u, v)의 유사도는 랜덤워크를 통해 산출한 확률 $P(v \vert u)를 통해 계산할 수 있다.

그리고 우린 이를 노드를 인코딩하여 근사하고자 하니 다음과 같은 식으로 정리할 수 있습니다.

\textbf{z}^T_u\textbf{z}_v \approx \;랜덤워크에서 \;노드\; u와\; v가\; 동시에 \;등장할 \;확률\\ \textbf{z}^T_u\textbf{z}_v \approx P_R(v \vert u)

이제 필요한 것은 모두 준비되었습니다.

인코더 : 룩업
그래프에서의 유사도 : 랜덤워크를 통해 산출한 확률 $P(v \vert u)$
임베딩 공간에서의 유사도 : $z_u$ 와 $z_v$ 의 내적

즉, 우리는 내적을 통해 두 노드가 랜덤워크를 통해 도달할 수 있는 확률을 근사할 것이다.

3-3. 장점

랜덤워크를 사용하면 다음과 같은 장점이 있습니다.

Expressivity : 확률로 표현되기 때문에 두 노드의 경로가 짧은 경우는 물론이고 경로가 긴 경우에도 이웃 정보를 잡아낼 수 있습니다.
Efficiency : 훈련 시 모든 노드를 고려할 필요없이 랜덤워크 시에 동시 등장하는 노드 쌍만 고려하면 되어 효율적입니다.

위에서 미리 언급했지만, 주어진 노드 u에 대해 이웃한 노드는 다음과 같이 정의됩니다.
$N_R(u)$ : 랜덤워크 전략 R에 의해 구해진 u의 이웃 노드 집합

3-4. 최적화 과정

Given G = (V, E)
Goal : to learn a mapping f : $u \to \mathbb{R}^d$ : $f(u) = z_u$
Objective :

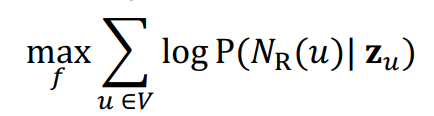
짧은 거리의 랜덤워크를 고정하여 R에 따라 각 노드마다 진행합니다.
각 노드 u마다 $N_R(u)$ 를 수집합니다. 이때 $N_R(u)$ 는 일반적인 집합과 다르게 중복이 허용됩니다. 랜덤워크시 반복하여 특정노드를 반복할 수도 있기 때문입니다.
다음 식에 따라 임베딩을 최적화합니다.

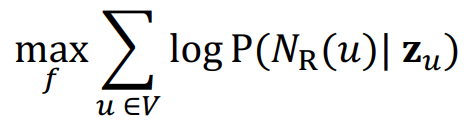
손실함수를 구하면 다음과 같이 될 것입니다.

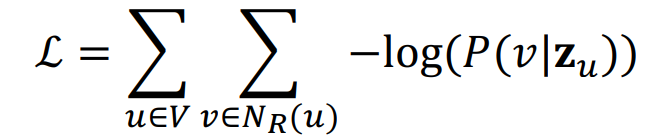
이때 확률은 소프트맥스 함수를 통해 구하게 됩니다.

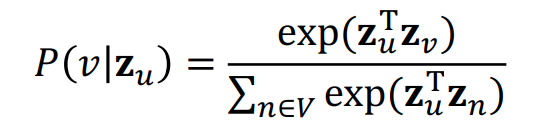
즉, 이웃노드가 등장할 확률이 높아지도록 임베딩 벡터가 최적화될 것입니다. 즉, 이웃 노드는 내적값이 커지고, 이웃하지 않은 노드 간에는 내적값이 작아지게 됩니다.

하지만 이와 같은 손실함수를 사용하는 것은 문제가 있습니다.

위와 같이 전체 노드가 두번 중첩되어 시간복잡도가 너무 커지게 됩니다.

3-5. Negative Sampling

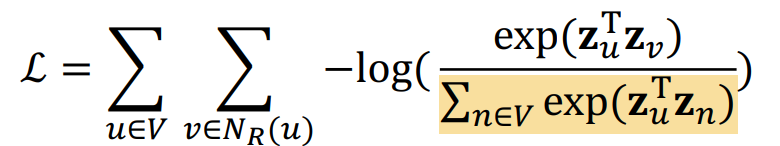
손실함수 식을 살펴보면 맨 앞의 V는 해결할 수 없습니다. 모든 노드에 대해 손실함수가 계산되긴 해야합니다. 하지만 두번째 V는 수정할 수 있습니다. 두번째 V는 정규화를 위한 항이기 때문입니다. 이를 근사하여 계산량을 줄일 수 있습니다.

소프트맥스에서 정규화 항을 근사하는 방법이 네거티브 샘플링입니다.

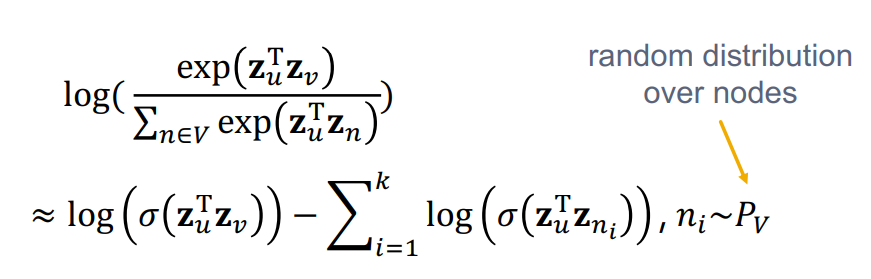
네거니브 샘플링은 위와 같은 방법으로 이루어집니다. 전체 노드에 대해 내적값을 구하는 대신 노드 u와 이웃하지 않은 노드 중 k개를 샘플링하여 사용하게 됩니다. 이때 앞의 시그모이드 항은 이웃 노드간 계산되는 이웃노드일 확률로 최대화됩니다. 뒤에 나오는 시그모이드 항은 u와 이웃하지 않은 노드와 계산되는 이웃노드일 확률로 최소화되게 됩니다.

즉, 이웃 노드 간의 확률은 높아지고, 이웃하지 않은 노드 간 확률은 낮아지도록 최적화되게 됩니다.

이때 k개의 노드는 각 노드의 degree 분포에서 샘플링하게 됩니다.
k가 커질수록 강건하게 근사할 수 있지만, 반대로 네거티브 샘플에 지나치게 편향(bias)될 수 있어 보통 5 ~ 20을 사용합니다.

손실함수는 SGD를 이용해 각 파라미터 최적화에 사용되게 됩니다.

4. Node2Vec

앞서 Deepwalk를 설명하면서 전략 R이 어떻게 구성되는지 자세한 설명이 없었습니다. 단순하게 각 시점마다 unifrom dist.를 통해 이동한다고 했습니다. 하지만 분명히 이보다 효과적으로 그래프의 정보를 임베딩할 수 있는 전략이 있을 것입니다. node2vec은 그 전략에 관한 설명이 주를 이룹니다.

node2vec이 deepwalk와 달라지는 점은 그래프에서 이웃 노드 집합 $N_R(u)$ 를 찾을 때 비교적 유연하게 대처할 수 있는 전략 R을 이용하여 노드 임베딩에 더욱 풍부한 정보를 인코딩하고자 하는 것입니다.

그 아이디어는 다음과 같습니다.

flexible, biased random walk를 이용하여 지역적 정보와 그래프 전체 정보 간의 트레이드오프 관계를 확보하는 것.

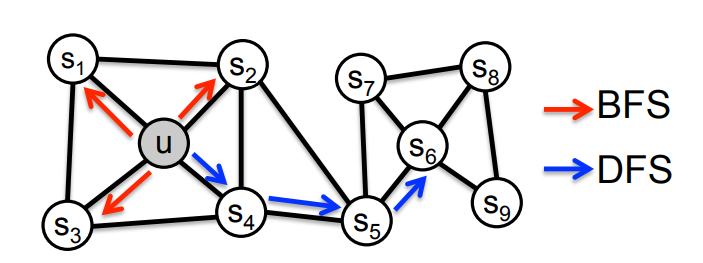
노드 u에서 시작하여 랜덤워크를 한다고 할 때 너비 우선 탐색 방식으로 진행한다면 노드 u 주변의 정보는 풍부하게 담을 수 있지만, 전체적인 구조를 담지 못합니다. 즉, 위 그림에서 오른쪽의 부분 그래프에 대한 정보를 u는 담지 못하게 됩니다. 반대로 깊이 우선 탐색 방식으로 진행하면 전체적인 구조에 대한 정보를 담을 수는 있지만 노드 u 주변의 정보가 부실해지게 됩니다. 결국 노드 주변을 얼마나 탐색하는지에 따라 local과 global 정보가 트레이드 오프 관계에 놓이는 것입니다. 그리고 node2vec은 이를 조절하여 탐색하는 전략 R을 세우는 것입니다.

4-1. Biased Random Walks

biased random walks는 두가지 파라미터가 있습니다.

p : 직전 노드로 돌아갈 확률을 정하는 파라미터
q : 직전 노드에서 먼 노드로 갈 확률을 정하는 파라미터

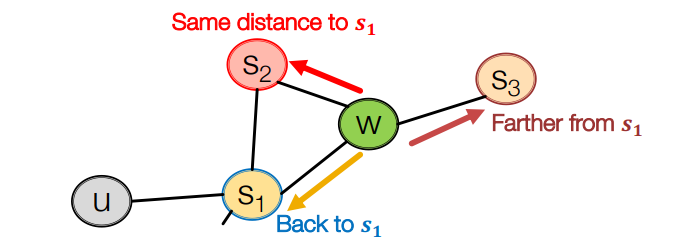
예를 들어 위 그림에서 랜덤워크는 $s_1$ 에서 w로 이동한 상태라고 할 때, 움직일 수 있는 방향은 세가지입니다.
1. $S_1$ : 직전 노드로 돌아가기
2. $S_2$ : 현재 노드와 직전 노드 간의 거리와 동일한 노드로 이동하기
3. $S_3$ : 현재 노드와 직전 노드 간의 거리보다 먼 노드로 이동하기

그리고 각 노드로 이동할 확률분포는 p와 q를 통해 정해지게 됩니다.

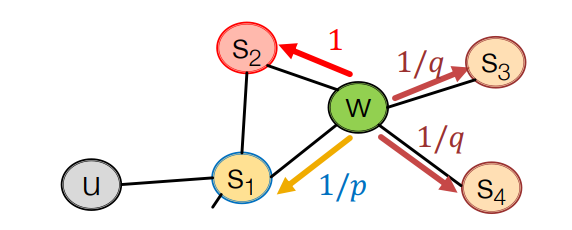
p와 q는 위 그림처럼 정규화되지 않은 확률로 작동하게 됩니다. 구체적으론 w에서 각 노드까지 거리를 계산하고, 거리마다 위의 세가지 방향 중 어떤 방향인지 분류하고, p와 q를 이용한 확률을 정규화하고, 그 확률에 따라 이동하는 것입니다. 이때 랜덤워크지만 그 확률분포가 uniform하지 않고 p와 q에 따라 biased 되기 때문에 biased random walk라고 합니다.

이때 만약 p가 작은 값을 가지게 되면 상대적으로 직전 노드로 돌아갈 확률이 크기 때문에 너비 우선 탐색과 비슷한 작동이 됩니다. 만약 q가 작은 값을 가지게 됩니다. 직전 노드와 현재 노드의 거리보다 먼 노드로 이동하기 때문에 깊이 우선 탐색과 비슷한 작동이 되게 됩니다.

4-2. Algorithms

전체적인 학습 알고리즘은 다음과 같습니다.
1. 랜덤 워크 확률을 계산합니다.
2. R 랜덤워크를 고정된 길이 l에 대해 모든 노드 u에서 실행합니다.
3. SGD를 이용하여 node2vec 목적함수를 최적화합니다.

node2vec의 장점은 선형적인 복잡도를 가지고 있다는 점입니다. 또한 위의 세 과정 모두 병렬화가 가능해 매우 빠르게 학습이 가능합니다.

다만, 그래프의 크기가 커질수록 임베딩 차원의 수가 커져야하는 단점이 있습니다 .

5. Embedding Entire Graphs

이전까지 노드 임베딩에 살펴봤다면, 이젠 그래프 임베딩에 대해 살펴보도록 하겠습니다.
그래프 임베딩이란 전체 그래프 혹은 부분 그래프를 임베딩 공간에 맵핑하는 것을 의미합니다. 이는 분자 구조를 분류하여 독성을 감지하는 등의 태스크에 활용될 수 있습니다.

5-1. Simple Approaches

단순한 방법으론 두가지가 있습니다.

Sum
앞서 배웠던 일반적인 노드 임베딩 방법을 (부분) 그래프에 적용합니다. 그 결과 해당 (부분) 그래프 각 노드마다 임베딩 벡터가 생성됩니다. 임베딩 공간에서 벡터의 위치는 상대적이므로 모든 노드의 임베딩 벡터를 아래 수식처럼 더하거나 평균내어 해당 (부분) 그래프의 임베딩 벡터로 사용합니다.
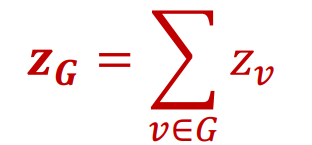
Virtual Node
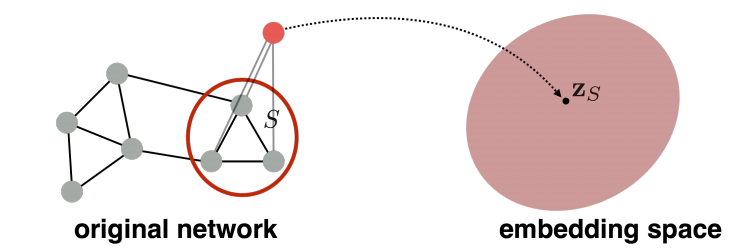
임베딩 하고자 하는 (부분) 그래프의 모든 노드와 연결된 가상의 노드를 생성합니다. 이 노드의 임베딩 벡터가 해당 (부분) 그래프의 임베딩 벡터라 간주하고 노드 임베딩을 실시하게 됩니다.

5-2. Anonymous Walk Embeddings

이보다 발전된 방식으로는 anonymous walk embedding이 있습니다.

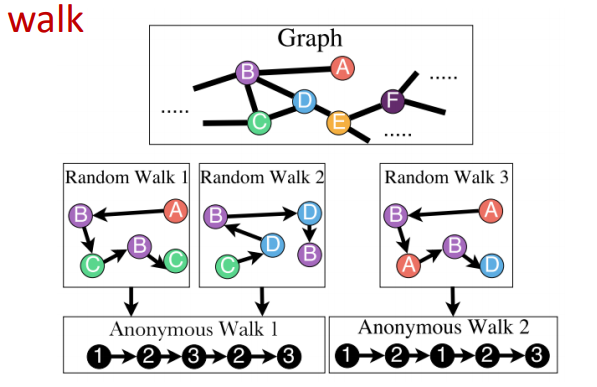
이는 위 그림과 같이 정해진 길이의 랜덤워크에 대해 각 노드의 인덱스를 지워 노드를 익명으로 만듭니다. 대신 랜덤워크에서 중복으로 등장한 노드에 대해서는 처음 등장시 매겼던 인덱스를 부여하게 됩니다. 그 결과 위 그림과 같이 Random Walk1과 2는 각기 다른 노드를 지났지만, 노드의 인덱스를 지우면 동일한 anonymous walk를 가지게 됩니다. 그래프의 입장에서 각 노드의 정보는 활용할 수 없고, 그 구조만 파악 가능하기 때문에 이와 같이 노드의 정보(인덱스)를 지우고 처리하는 것이 유의미해집니다.

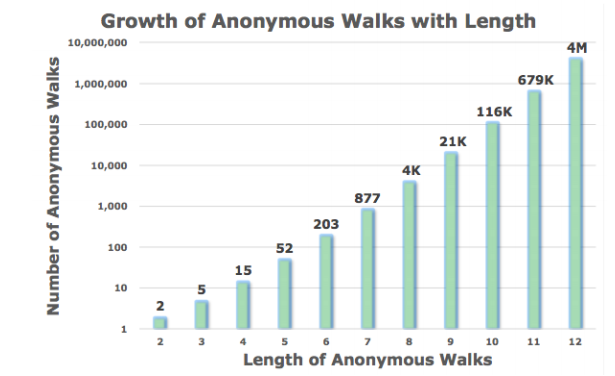
Anonymous Walk Embedding은 길이와 익명처리된 노드 수에 따라 지수적으로 증가하는 꼴이 됩니다. 예를 들어 길이가 3일 경우 익명처리된 노드는 1, 2, 3 총 세개가 될 수 있기 때문에 walks의 종류는 다음과 같이 총 5개가 됩니다.

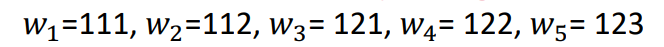
임베딩 벡터는 다음과 같이 생성됩니다.
1. l 스텝에 대해 anonymous walk $w_i$ 를 실행하고 그 빈도를 기록합니다.
2. 임베딩 벡터 $Z_G$ 의 i번째 element로 $w_i$ 의 빈도를 사용합니다.

예를 들어 l = 3 이라면 위에서 언급한 바와 같이 임베딩 벡터는 5차원이 됩니다. 각 element는 다음과 같은 anonymous walk를 가지게 됩니다.
[111, 112, 113, 121, 122, 123]

anoanymous walk를 샘플링하기 위해선 독립적으로 m번의 random walk를 실행해야 합니다. 이때 적절한 실행횟수 m을 구하는 공식은 다음과 같습니다.

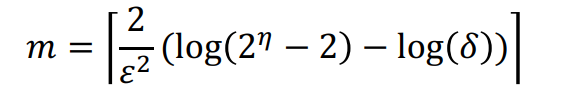
$\epsilon$ : 오차 하한
$\delta$ : 오차 상한
$\eta$ : 길이가 l일 때의 총 anonyomous walk 수

5-3. Learn Walk Embeddings

단순히 각 walk의 빈도수를 임베딩 벡터로 사용하기 보단 각 walk 역시 임베딩하여 사용하는 방법이 있습니다.
이때의 그래프 임베딩 $\textbf{Z}_G$ 는 다음과 같습니다.

\textbf{Z} = (z_i : i = 1, ..., \eta)

핵심 아이디어는 다음과 같습니다.
window size를 $\Delta$ 라고 할 때, 동일한 노드에서 출발한 $w_{t-\Delta}, ..., w_{t + \Delta}$ 를 이용해 $w_t$ 를 예측하자.
여기서 인접한 walk란 아래 그림과 같이 동일한 노드에서 출발한 walk를 의미합니다.

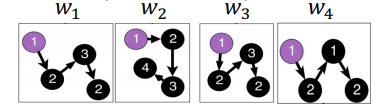
목적함수는 다음과 같습니다.

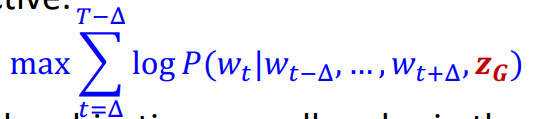
전체 학습 과정은 다음과 같습니다.
1. 노드 u, 길이 l에 대해 개별적인 T번의 랜덤 워크를 수행하여 다음과 같은 $N_R$ 을 구한다. 이때의 $N_R(u)$ 은 이전의 이웃 노드 집합이 아니라 동일한 노드 u에서 시작한 random walk의 집합입니다.

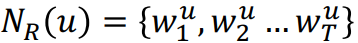
2. $\eta$ 사이즈의 윈도우를 이용해 해당 랜덤워크를 예측하는 태스크를 수행합니다.
이때의 목적함수는 다음과 같습니다.

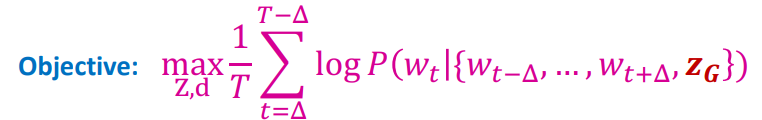
3. 소프트 맥스 함수를 이용해 예측이 진행됩니다.
이때 랜덤워크 벡터들은 평균을 내어 그래프 벡터와 concat되어 입력값으로 사용됩니다.

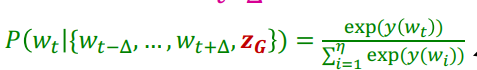
해당 모델을 발표한 논문(Anonymous Walk Embedding, Sergey Ivanov, 2018)에서는 단어 벡터를 이용해 문단 벡터(Paragraph Vector)를 생성하는 NLP 분야의 논문(Distributed Representations of Sentences and Documents, Quoc Le, 2014)을 차용하여 해당 학습 방법론을 사용했습니다. 해당 NLP 논문에선 아래 그림처럼 동일한 문단에서 나온 단어와 해당 문단의 벡터를 concat/average하여 중심 단어를 예측하는 태스크를 수행하여 문단 벡터를 생성했습니다.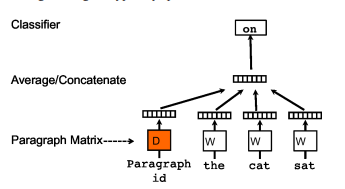

단어와 문단의 관계처럼 하나의 그래프의 동일한 노드에서 나온 random walk를 이용하여 해당 노드에서 나온 다른 random walk를 예측할 수 있을 것입니다. 이를 이용하여 학습이 진행됩니다.

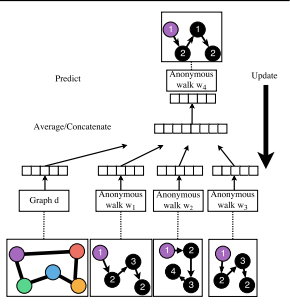
5-4. Graph Embedding

위와 같은 학습 과정을 통해 그래프 전반의 정보는 인코딩 되어 $\textbf{z}_G$ 가 만들어집니다. $\textbf{z}_G$ 를 이용해 실제 태스크를 수행하는 방법은 크게 두가지가 있습니다.

두 그래프 벡터를 커널을 통과하여 사용하는 방법 $\textbf{z}^T_{G1}\textbf{Z}_{G2}$
$\textvf{z}_G를 직접 신경망의 입력값으로 사용하는 방법

6. How to Use Embeddings

임베딩 벡터 $\textbf{z}_i$ 를 사용하는 방법은 다음과 같습니다.
1. 클러스터링, 소셜 네트워크 군집화 $z_i$ 를 하나의 점으로 간주하고 군집화를 실행합니다.
2. 노드 분류: $z_i$ 를 이용해 i 노드의 레이블을 예측합니다.
3. 링크 예측 : (i, j)의 엣지를 두 노드의 임베딩 벡터 $(z_i, z_j)$ 를 이용해 예측할 수 있습니다.

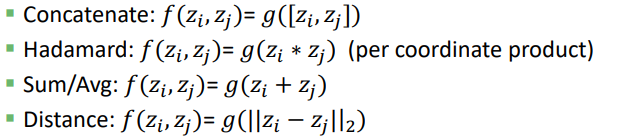
이때 hadamard나 sum/avg는 교환법칙이 성립하므로 undirected graph에 적용하기 좋은 방법론입니다.
4. 그래프 분류 : 노드 임베딩을 결합하여 그래프 임베딩을 생성하거나 anonymous random walks를 이용해 만든 그래프 임베딩을 통해 분류 태스크를 수행할 수 있습니다.