[CS224W] Lecture 4 - PageRank

김재희·2021년 8월 6일

목록 보기

4/11

이번 강의에선 구글이 과거 "구글"이 될 수 있었던 중요한 검색 알고리즘 페이지 랭크를 다룰 것이다. 지금이야 무척이나 다른 알고리즘을 사용하지만 구글의 두 창업자가 페이지 랭크를 이용해서 처음 구글을 공개했을 때만 해도 무척이나 좋은 성능을 보이는 획기적인 알고리즘이었다고 한다관련 기사.

0. Intro

이 강의 전반의 목표는 다음과 같다.

그래프를 행렬로 다루기
-> 랜덤 워크를 통해 노드의 중요도를 판단할 수 있다.
-> MF(Matrix Factorization)을 통해 노드 임베딩을 얻을 수 있다.
-> 이전의 강의들에서 배웠던 노드 임베딩을 MF로 볼 수 있게 된다.

즉, 그래프를 행렬로 보면서 MF가 가능해지고 그래프에 대한 다양한 변수가 만들어질 수 있는 것이다.

1. Web

인터넷 세상을 멀리서 보면 어떻게 그래프로 볼 수 있을까?

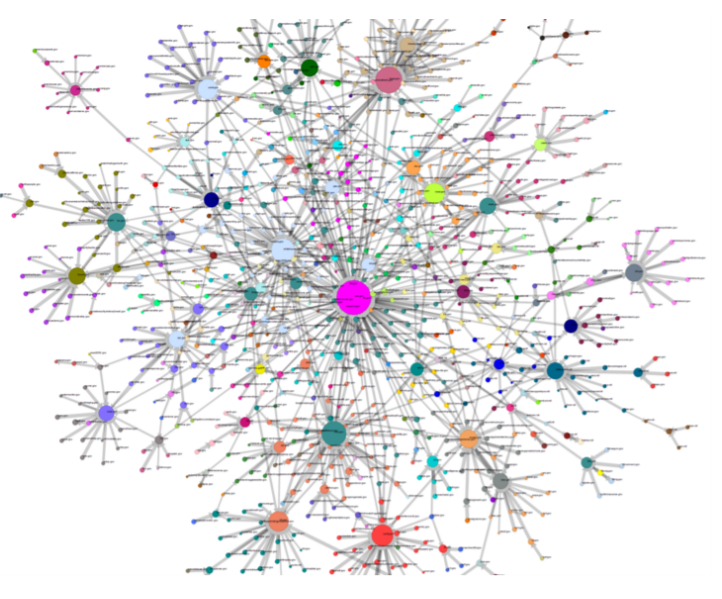
각 웹사이트 페이지를 노드로, 페이지에 걸려있는 다른 페이지에 대한 하이퍼링크를 엣지로 볼 수 있지 않을까? 즉, 페이지들이 하이퍼링크로 연결된 그래프구조라고 볼 수 있을 것이다. 하지만 이때 다크웹과 같은 표면적으로 잡히지 않는 웹사이트나 일시적으로 생성되고 사라지는 광고성 사이트들을 어찌 취급할지에 대한 사소한 문제가 발생한다. 이러한 문제는 잠시 접어두고, 구조가 잘 짜여진 웹사이트만 다룬다고 생각해보자.

초기의 인터넷은 하이퍼링크가 방향성이 있었다. 즉, 위에 내가 걸어놓은 신문기사와 같이 내 벨로그 페이지에서 신문 페이지로 이동하도록 하는 통로였다. 하지만 현재 인터넷은 많은 연결들이 상호작용의 결과 발생한다. 즉, A 에서 B로 이어지는 것이 아니라, A와 B가 C에서 댓글을 달고, A가 B의 페이지에서 좋아요를 누르면서 이루어진다. 이러한 연결들은 하이퍼링크를 통해 잡히지 않는다. 하지만 페이지랭크는 하이퍼링크를 기반으로 이루어지니 이러한 요소들 역시 잠시 접어두자.

이러한 노드와 엣지를 가지고 있는 구조는 꽤 많다고 한다.

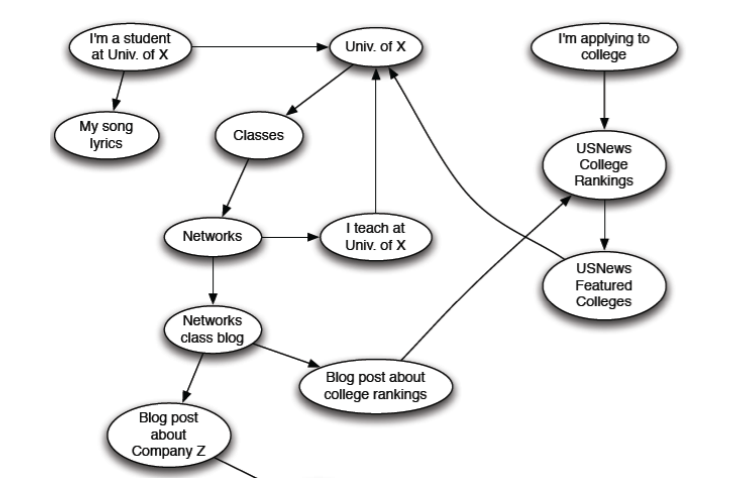
기본적으로 위에서보이듯 웹사이트가 그러한 구조를 띄고 있고,

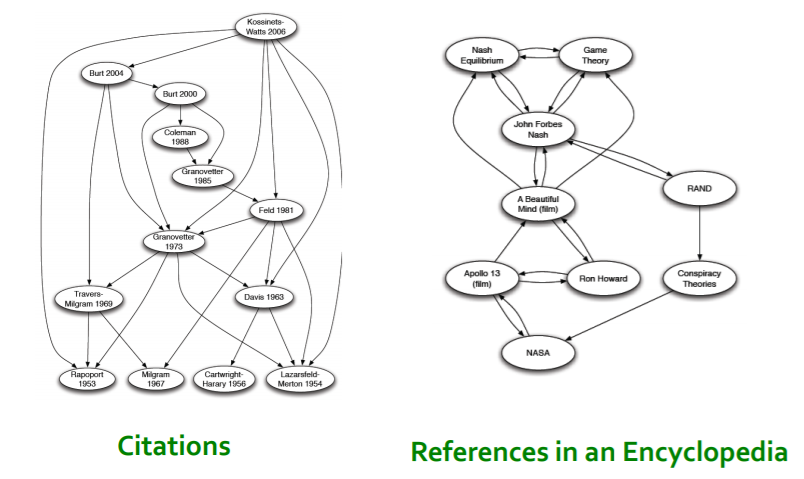
이외에도 인용 구조를 보면 논문(노드)과 논문에 사용된 인용(엣지)으로 구성되어 있다.

여기까지 봤다면, 정리해보자.
웹페이지는 directed graph로 간주할 수 있으며, 주어진 사이트 v에서 다른 사이트 v'로 이동할 수 있는지 고려할 수 있다. 이 상황에서 각 페이지의 중요도를 매길 수 있게 된다. 특정 페이지가 수많은 페이지에서 하이퍼링크를 받을 수도 있고, 특정 페이지가 수많은 페이지에 하이퍼링크를 줄 수 도 있다. 이를 통해 웹은 다양한 부분 그래프 구조를 이루고, 여기서 우리는 각 노드 즉, 웹페이지의 중요도를 판별할 수 있을 것이다.

2. Links as Votes

2-1. Importance of Page

페이지의 중요도를 매길 때 링크를 사용할 수 있다고 이야기했다. 이때 들어오는 링크를 사용해야 할까 나가는 링크를 사용해야 할까? 나가는 링크를 사용하는 것은 부적절할 수 있다. 특정 페이지가 중요하게 보이고자, 이곳 저곳으로 나가는 링크를 생성할 수 있기 때문이다. 하지만 들어오는 링크는 그렇지 못하다. 전적으로 다른 페이지로부터 링크를 받아야 하기 때문에, 해당 페이지가 링크를 받을만한 가치가 있는 페이지가 되어야 한다. 즉, 링크를 많이 받을수록 더 중요한 페이지일 것이다.
여기서 또 한가지 추가할 수 있다. 스탠포드 대학교 CS224W가 링크한 사이트가 더 중요할까, 내가 방금 만든 사이트에서 링크한 사이트가 더 중요할까? 당연히 전자가 더 중요할 것이다.

즉, 중요한 사이트에서 더 많은 링크를 받을수록 중요한 사이트이다.

위 문장은 결국 우리가 지금 recursive하게 문제를 풀려고 한다는 것을 암시한다. 중요한 사이트를 이용해 중요한 사이트를 계산하고자 하기 때문이다.

2-2. PageRank: The Flow Model

위의 논리를 계산하는 과정은 다음과 같이 이루어진다.

각 노드는 도착하는 링크의 합으로 중요도를 가진다.
각 out link는 도착하는 노드로의 투표로 간주한다.
각 out link는 출발하는 노드의 중요도 / 출발하는 노드의 out link 수로 투표수를 가지게 된다.

말로만 보면 모호하니 식과 예시를 살펴보자.

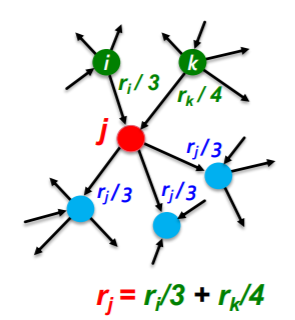
위의 그림에서 i 노드가 1의 중요도를 가진다고 생각해보자. 그러면 i노드는 총 3개의 out link를 가지고 있으므로 $d_i = 3$ 이다. 또한, i노드의 out node의 vote은 ${r_i \over d_i} = {1 \over 3}$ 이다.
j노드는 총 두개의 in link를 가지고 있으므로 $r_j = {r_i \over 3} + {r_k \over 4}$ 가 된다.

그러면 결국 각 노드의 중요도는 in link와 이웃 노드로 정의된 방정식으로 정의된다.

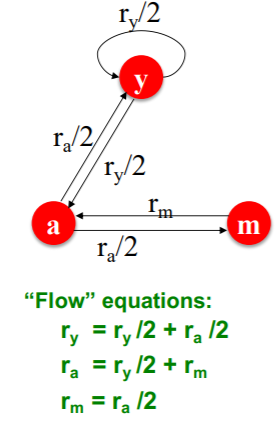
위와 같이 3개의 노드만 있는 상황에서 연립방정식으로 표현할 수 있으니, 가우시안 소거법 등을 통해 연립 방정식의 해를 구하면 되지 않을까? 문제는 현대의 인터넷 세상이란 너무 페이지가 많아서, 이렇게 풀 수 없다는 점이다.

2-2. PageRank: Matrix Formulation

다음과 같은 Stochastic Adjacenty Matrix M이 있다고 해보자.

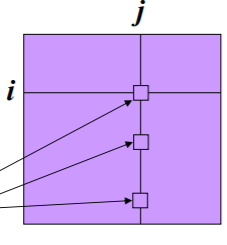
shape은 행과 열 모두 페이지의 수만큼 가지므로, $m \times m$ 행렬이다. 이때 각 열의 합은 1이 되고, 각 열은 해당 열 페이지에서 다른 페이지로의 연결을 나타내는 확률분포가 된다. 즉, j 페이지가 $d_j$ 개의 out link를 가진다고 하면

M_ij = {1 \over d_j} \; (j \to i)

가 된다.
이때 중요도 벡터 r은 각 페이지의 중요도를 element로 가지는 벡터로서 $r_i$ 는 i 페이지의 중요도 점수를 나타낸다. 또한 $\sum_i r_i = 1$ 이다.

이를 위의 요소와 결합해 생각해보자. 모든 노드가 중요도를 가지고 있을 때, 새로운 중요도는 다음과 같이 정의된다.

r_k = \sum_{i \to j} {r_i \over d_i}

이를 M 행렬과 r 벡터로 나타내면 다음과 같다.

r_{new} = M \cdot r_{old}

문제가 조금 간단해지는 모습이다. 위의 노드 3개의 예시를 나타내면 다음과 같아진다.

2-3. Random Surfer

이제 이전에 배웠던 알고리즘들과 페이지랭크를 연결시켜볼 차례이다. 랜덤워크는 랜덤하게 노드를 옮겨다니는 알고리즘을 기반으로 한다. 이번엔 랜덤하게 페이지를 서핑하는 사람이 있다고 간주하자. 이 사람이 시점 t에 i번째 페이지에 있었을 때, 다음 시점 t + 1에 있을 페이지는 uniform dist.를 따른다면, 페이지 랭크 개념과 이어질 수 있다.

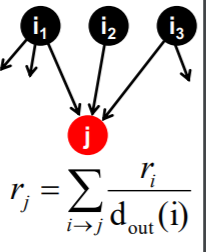
위 그림에서 $i_1$ 페이지에 있는 사람이 j 페이지로 이동할 확률은 $1 \over d_i{1}$ 이기 때문이다. 그리고 역으로 j 페이지의 관점에서 각 페이지 $i_1, i_2, i_3$ 에서 j로 왔을 liklihood는 ${1 \over d_{i1}},{1 \over d_{i2}}, {1 \over d_{13}}$ 로 볼 수 있다.

이제 벡터 p(t)를 각 elementary 페이지에 인터넷 서퍼가 시점 t에 있을 확률분포라고 생각해보자. 그러면 행렬 M과 연관지어 다음과 같이 생각할 수 있다.

p(t + 1) = M \cdot p(t)

그런데 만약 우리가 p(t)를 정확하게 추론했다면, 다음과 같은 관계가 성립할 수 있다.

p(t+1) = M \cdot p(t) = p(t)

즉, 시점이 변화하더라도 각 페이지에 있을 확률은 변하지 않는 것이다. 당연하다. 정확한 각 페이지에 있을 확률은, 서퍼가 특정 페이지에서 다른 페이지로 이동한다고 해도, 시점이 달라진다고 해도 변화하지 않을 것이기 때문이다. 이를 stationary dist.라고 한다.

그렇다면 우리는 $r_{new}$ 와 $r_{old}$ 의 관계를 계산하는 것이 아니라, 다음과 같은 r을 찾는 문제를 풀면 된다.

r = M \cdot r

시점의 영향을 받지 않는 stationary dist. r을 찾자.

2-4. 다른 알고리즘과의 관계

이와 같은 수식 $ r = M \cdot r$은 다른 알고리즘과 페이지 랭크의 관계를 알려주고 있다.

이전에 아이겐 벡터 중심성에 대해 다뤘는데 그 때 인접행렬 A를 이용해 다음과 같이 계산했다.

\lambda c = Ac

우리가 현재 다루고 있는 식 역시 위와 같이 표현할 수 있다. 단순 인접행렬이 stochastic adjecency matrix로 대치되고, 아이겐 벨루가 1일 따름이다.

1 \cdot r = M \cdot r

즉, 랭크 벡터 r은 행렬 M의 아이겐벡터가 된다.
또한, 초기 벡터 u에서 유한번의 M power $M^K u$ 가 장기적으로 서퍼의 분포를 담고 있다고 할 때, $ r = M^T u = M r$일 것이다(이는 Katz 알고리즘과의 연관성이 된다.).
이때, 아이겐 벨루가 1인 아이겐 벡터를 pricipal eigenvector라고 한다.

자 우린 이제 r을 구하면 되고, 이를 Power Iteration을 통해 구할 것이다.

2-5. Solving PageRank

그럼 어떻게 페이지 랭크를 풀게 될까? Power Iteration을 이용한다고 했다. 그 개념은 단순하다. $r_{new} = M \cdot r_{old}$ 를 계속해서 반복해서 수렴할때까지 계산한다. 수렴조건은 아래와 같다.

\sum_i \mid r^{t+1}_i - r^t_i \mid < \epsilon

즉, 모든 페이지가 업데이트 되는 양의 합이 $\epsilon$ 보다 작으면 수렴했다고 간주하고, 반복을 멈추게 되는 것이다.
전체 알고리즘을 살펴보면 다음과 같다.

Initialize: $r^0 = [{ 1\over N}, ..., {1 \over N}]^T$
Iterate: $r^{t + 1} = M \cdot r^t$
Stop when $\mid r^{t+1}_i - r^t_i \mid_1 < \epsilon$

이때 l1 norm 외에 l2 norm 등을 사용할 수도 있다고 한다. 일반적으로 50회 정도 반복하면 수렴한다고 하는데, 처음 접할 때 복잡했던 문제가 단순하게 행렬과 벡터의 내적을 통해 해결된다는 것이 놀랍다고 할 수 밖에 없다. 매우 단순한 연산이지만 매우 강력해진 것이다.

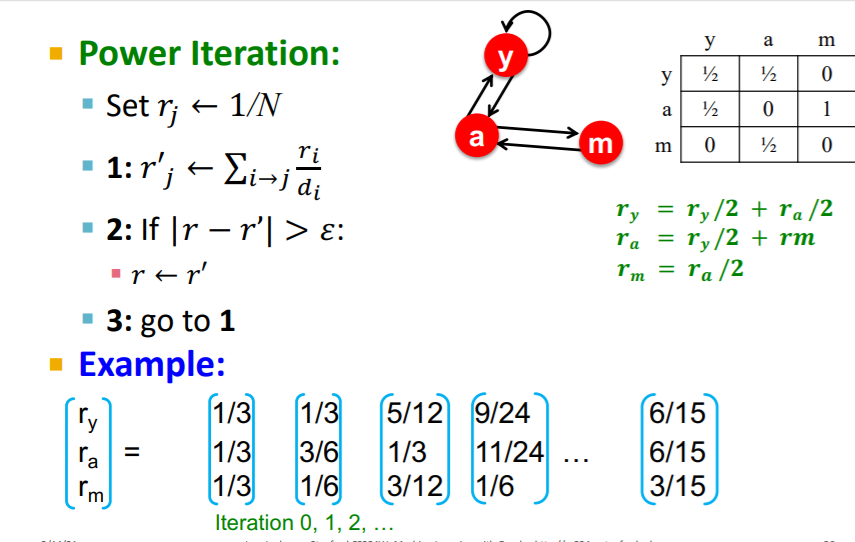
실제로 돌아가는 예시를 보자면 위와 같다. 초기에는 모두 $1\over 3$ 으로 같았던 페이지 중요도가 반복하면서 달라지게 되고, 결국 특정값으로 수렴되는 모습을 보이고 있다. 실제로 연립 방정식의 해와 동일한 모습을 보이고 있다.

하지만 아직 세가지 질문이 해결되지 않았다. 간단한 해결책의 과정은 절대 간단할 리 없는 법이다.

정말 위의 식이 수렴을 보장할 수 있는가?
수렴하는 지점이 우리가 원하는 지점인가?
결과물이 합리적이라고 볼 수 있는가?

2-6. Problems

하지만 페이지랭크가 완벽한 것은 아니다. 크게는 두가지 문제점이 존재하는데 다음과 같다.

Spider Trap : 어떤 페이지 그룹은 모든 out link가 스스로 연결되어 있는 spider trap을 구성하고 있다. 이 경우에도 중요도가 다른 페이지들로 전달되지 않고, 해당 그룹에 계속 고이게 된다.
Dead End어떤 페이지들은 dead end를 가지고 있다. 즉, out link가 존재하지 않고, 중요도를 다른 페이지로 전달하지 않는다.

하나씩 자세히 살펴보고 해결책 역시 알아보자.

2-6-1. Spider Trap

위와 같이 극단적인 경우의 그래프가 있다고 해보자. 이때 a에서 b로 가는 엣지는 있지만 b에서 나오는 엣지는 존재하지 않는다. 이 경우 a는 중요도를 계속해서 b로 보내어 결과적으로 a 자신의 중요도는 0이 되어버리고, b는 계속해서 중요도를 받기만 하기 때문에 중요도가 1이 되어버린다. 만약 a가 거대한 그래프의 일부라 하더라도 변하는 것은 없다. 반복될 수록 b로 중요도가 흘러들어가서 모든 중요도를 b가 흡수하게 된다.

이 때의 해결책은 랜덤 서퍼는 $\beta$ 의 확률로 링크를 따라가게 되고 $1-\beta$ 의 확률로 랜덤한 페이지로 이동하도록 하는 것이다.

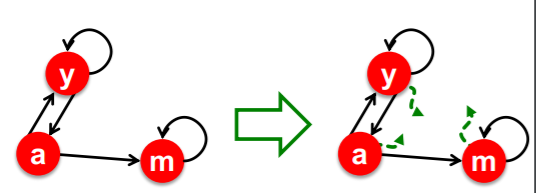
이를 통해 우리는 spider trap을 만드는 노드 집합에 대해서 중요도가 고이지 않고, 노드 집합 외부로 중요도가 흐르게 만들 수 있다.

2-6-2. Dead End

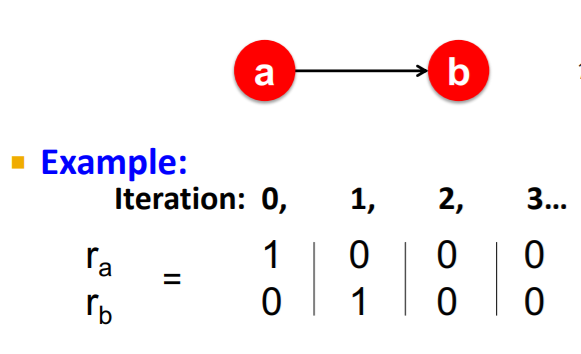
다시 위와 같은 극단적인 그래프를 가정해자. 이때, a에서 b로 항하는 엣지는 있지만, b는 자기 자신으로 도는 엣지조차 존재하지 않는다. 이 경우 a에서 b로 중요도가 흘러가는데, b는 중요도를 그 어느곳으로도 전달하지 않아 중요도가 그냥 사라져 버린다. 즉, $r = M \cdot r$ 에서 r이 더이상 확률 분포가 되지 못하는 것이다.

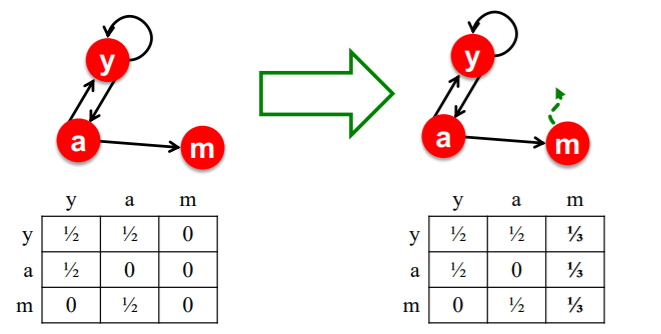
이때의 해결책 역시 랜덤하게 다른 페이지로 이동하게 하여 해결한다. 하지만 spider trap과 다른 점은 dead end에선 무조건 다른 페이지로 이동하게 하는 것이다. 즉, 랜덤 서퍼가 dead end에 도달하게 되면 uniform dist.에 따라 다른 노드로 중요도를 전달하게 된다.

2-7. How Teleport Solve the problems?

그럼 어떻게 이런 텔레포트가 문제를 해결한 것일까?
1. spider-trap
사실 스파이더 트랩의 경우 수학적으로 문제가 되지 않는다. 중요도가 그래프의 어딘가로 지속적으로 전달되기 때문에, r 벡터가 확률 분포의 꼴을 유지하기 때문이다. 하지만 그 모양이 애시당초 설정한 모양과 달라지는 것이 문제이다. 즉, spider trap 외부의 노드는 중요도가 0이 되고, 내부는 1에 가까워지는 것은 현실적이지 못하다.

dead end
데드 엔드의 경우 더이상 행렬 M의 해당 노드가 확률분포를 가지지 못하기 때문에, 전제조건을 위반하여 수학적으로 문제가 된다. 즉, 수학적으로 전제조건을 만족시키기 위해 uniform dist.를 사용하여 확률 분포의 꼴을 만들어준 것이다.

2-8. Google's Solution

구글의 실제 페이지 랭크 수식은 다음과 같다.

r_j = \sum_{i \to j} \beta {r_i \over d_i} + (1- \beta) {1 \over N}

여기서 행렬 M은 전처리를 통해 dead end를 지우게 된다. 앞서 언급한 텔레포트를 통해 dead end를 uniform dist.로 변환시킨다.

이를 Google Matrix G로 표기하면 다음과 같다.

G = \beta M + (1-\beta)[{1\over N}]_{N \times N}

즉, 본래의 M 행렬을 $\beta$ 만큼 사용하고, 텔레포트를 $1-\beta$ 만큼 사용한다. 랜덤워크의 관점에서는 $\beta$ 만큼 엣지를 타고 이동하게 되고, $1-\beta$ 만큼 텔레포트로 이동하게 된다.

위에서 언급한 예시를 텔레포트 개념까지 삽입하여 보게 되면 위와 같다. 이때, m 노드는 spider trap으로 작동하여 다른 노드에 비해 지나치게 중요도가 높게 평가된 것을 볼 수 있다. 이 상황에선 $\beta$ 를 낮추어 텔레포트가 더 자주 일어나게 하여 m 노드에서 중요도가 더 자주 빠져나갈 수 있도록 하여 해결할 수 있다.

좀 더 복잡한 페이지 랭크 구조는 위와 같은데, 여러 노드에서 링크를 받을 수록 중요도가 높아지고(B 노드) 중요 노드에서 링크를 받을수록 중요도가 높아지고(C노드) 중요하지 않은 노드에서 링크를 받을수록 중요도가 비교적 낮아지고(E노드) 링크를 받지 않더라도 중요도를 가지고 있는(녹색 노드들) 모습을 보이고 있다.

3. Random Walk with Restarts & Personalized PageRank

페이지 랭크의 변형을 살펴보자.
다음과 같은 추천시스템이 있다고 하자.

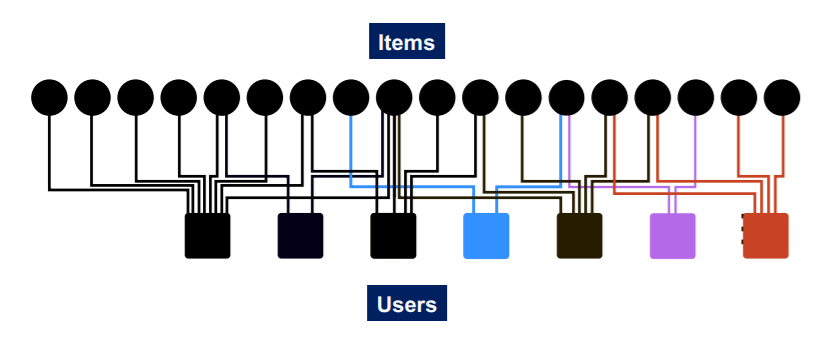
즉, Bipartite Graph의 상항이다. 이때 특정 아이템 Q를 구매한 사용자에 대해 어떤 아이템을 추천해줄지 페이지 랭크 알고리즘을 통해 계산하고자 한다. 이때, 어떠한 아이템이 서로 관련이 있는지 파악해야하는데, 어떻게 두 아이템 간의 관계를 파악해야 할까?

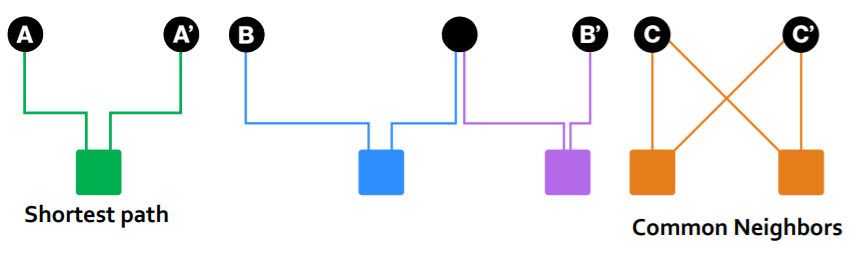
(A, A'), (B, B'), (C, C')의 짝에서 직관적으로 B가 제일 관계가 멀어보이고, A가 중간인 것 같고, C가 가장 가까운 관계인 것 같다.

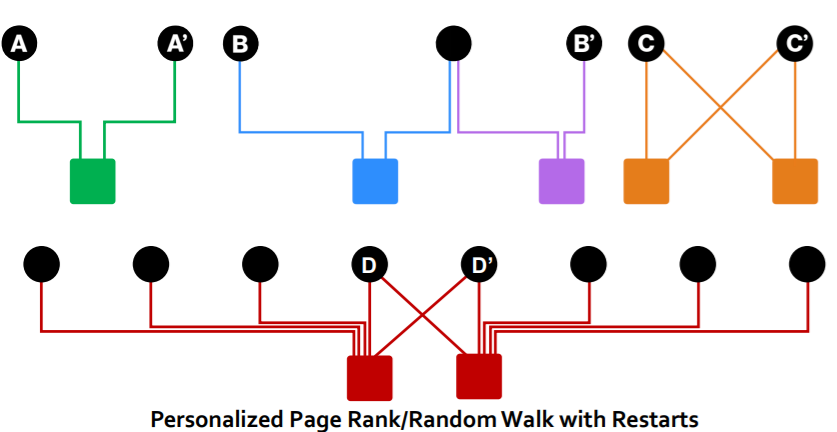
또한 D는 두 유저가 모두 이것저것 구매하는 성향으로 인해 우연히 D와 D'를 모두 구입했을 수 있기 때문에, C보다는 덜 연관된 것 같아보인다.

이를 어떻게 수학적으로, 알고리즘으로 구현할 수 있을까?

우리가 살펴볼 두 알고리즘은 페이지랭크와 다음과 같은 차이가 있다.

PageRank:
노드를 중요도를 기반으로 랭크를 매긴다.
전체 노드를 집합 S로 간주하고, 집합 S에서 랜덤하게 텔레포트한다.
Personalized PageRank:
노드 간의 근접 정도를 랭크를 매긴다.
부분 노드 집합 S에서 랜덤하게 텔레포트한다.
Random Walks with Restarts:
특정 노드 Q를 집합 S로 간주하고 무조건 Q로 텔레포트한다(restart).

여기서 세 알고리즘이 매우 달라보이지만 사실 거의 동일하다. 위에서 구글 행렬 G를 다음과 같이 정의했다.

G = \beta M + (1-\beta)[{1\over N}]_{N \times N}

위에서 자세히 살펴보면 두번째 행렬 $[{1\over N}]$ 이 텔레포트와 관련이 있는 행렬임을 알 수 있다. 위의 세 알고리즘은 이 행렬만 건드리고 있다.

personalized PageRank
텔레포트 노드에서 (i, j) element는 j노드에서 i 노드로 텔레포트될 확률을 의미한다. Personalized PageRank에선 모든 노드에 대해 uniform dist.로 텔레포트하지 않고, 정해진 노드 집합 S에 대해서만 uniform 혹은 가중치가 반영된 분포로 이동하게 된다. 즉, 텔레포트 행렬을 T이라 정의하면 $T_{j}$ 열벡터 $[T_{1j}, T_{2j}, ..., T_{Nj}]$ 는 다음과 같이 표현될 것이다.
$[T_{1j}, T_{2j}, ..., T_{Nj}] = [0.2, 0, 0, 0, 0, 0.4, 0, 0, 0.4]$
위에서 0이 아닌 값을 가지는 노드만 부분집합 S에 해당하는 노드가 된다.
Random Walks with Restarts
이 알고리즘은 부분집합 S에 restart할 노드 하나만 담겨있다. 즉, 다음과 같이 $T_j$ 의 열벡터가 구성된다.
$[T_{1j}, T_{2j}, ..., T_{Nj}] = [0,0,0,0,0,0,0,0,1,0,0,0,0]$
restart에 해당하는 열벡터의 확률이 1인 것을 볼 수 있다.

전체 알고리즘은 Personalized PageRank와 Random Walks with Restarts가 아래와 같이 동일하다.

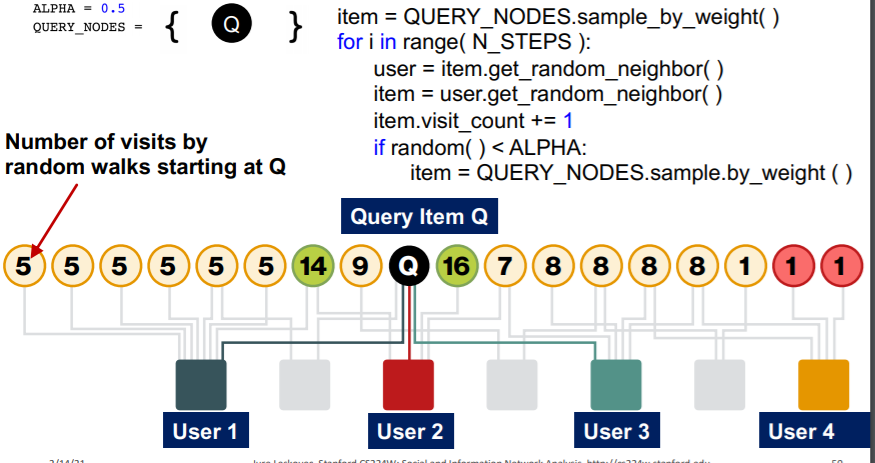
여기서 ALPHA는 각 랜덤워크 시점마다 초기값으로 돌아갈 확률이다. 즉, 기존의 랜덤워크처럼 진행하되, 초기값으로 돌아갈 수 있는 것이 두 알고리즘의 특징이다. 이는 페이지랭크가 기본적으로 랜덤워크를 사용하고 간단한 행렬 연산을 통해 구현했기 때문에 가능한 일이다.

결국 두 알고리즘 모두 텔레포트 행렬만 조정하여 사용하고 나머지는 페이지 랭크와 동일한데 어떻게 이를 통해 두 노드 간의 유사도를 고려하는 좋은 알고리즘이 될 수 있을까?

이는 해당 알고리즘이 유사도에 대한 다양한 다음 요소들을 모두 아우를 수 있기 때문이다.

다수의 엣지
다수의 경로
직접 혹은 간접 연결
사용자 노드 혹은 아이템 노드의 degree

시작점이 정해져 있는 랜덤워크는 결국 시작점으로부터 각 노드까지의 경로와 연결의 정도를 측정할 수 있게 된다.

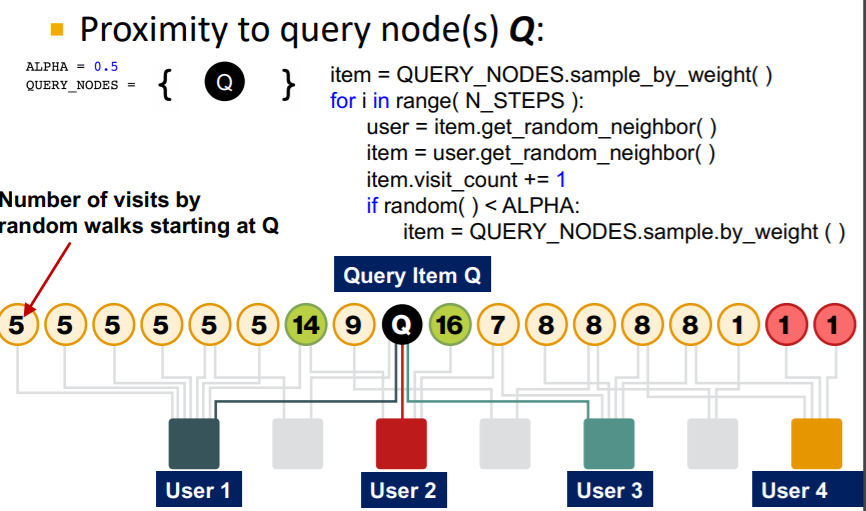
즉, 시작 노드와 특정 노드 간에 엣지가 많거나, 경로가 많거나, 직접 연결되어 있거나, degree가 낮은 사용자로 연결되어 있다면 랜덤워크에서 많이 방문하게 되고, 유사도가 높아질 수 밖에 없는 것이다.

4. Matrix Factorization

4-1. Simple Matrix Factorization

이전에 인코더는 임베딩 룩업을 통해 이루어질 수 있다고 했다. 임베딩 행렬 $Z$ 의 열벡터이자, 노드 v와 u의 임베딩 벡터의 내적인 $z^T_vz_u$ 는 u와 v가 비슷한 노드라면 최대화되는 목적함수를 가져야 한다. 즉, 비슷한 노드의 내적은 최대화 되도록 목적함수가 구성되어야 한다. 이때 가장 단순한 "비슷한 노드"라는 개념은 두 노드가 엣지로 연결되어 있을 때를 의미할 수 있을 것이다. 즉, i 노드와 u 노드가 유사하다면 인접행렬 A에서 $A_ij = 1$ 이어야 한다. 또한, 이를 벡터의 내적과 연결해보면 다음과 같아야 한다.

z^T_vz_u = A_{u, v}

즉 아래 그림과 같다.

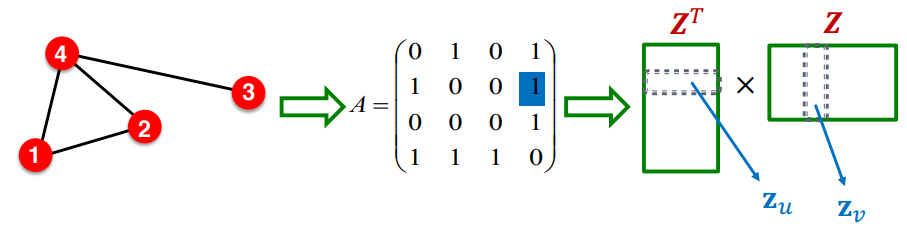
그런데 이를 행렬 연산으로 확장하면 다음과 같다.

Z^TZ = A

즉, 인접 행렬 A가 임베딩 행렬 Z로 분해된 것을 볼 수 있다.
하지만 실제로는 임베딩 벡터의 차원 d가 그래프의 정보를 담기엔 부족할 수밖에 없고, 우리는 결국 Z를 통해 A를 근사할 수 밖에 없다. 이때의 목적함수는 다음과 같다.

min_Z \lVert A - Z^TZ \rVert_2

이전의 강의에서 소프트 맥스를 l2 norm 대신에 사용하였으나, A를 임베딩 행렬 Z로 근사하려고 하는 목표는 크게 다르지 않다.

4-2. Random Walk-based Similarity

딥워크나 node2vec의 경우 보다 복잡한 개념으로 노드 유사도를 정의하고 있다. 이때 랜덤워크를 사용하게 되는데, 이로인해 다음과 같은 복잡한 행렬분해가 이루어진다.

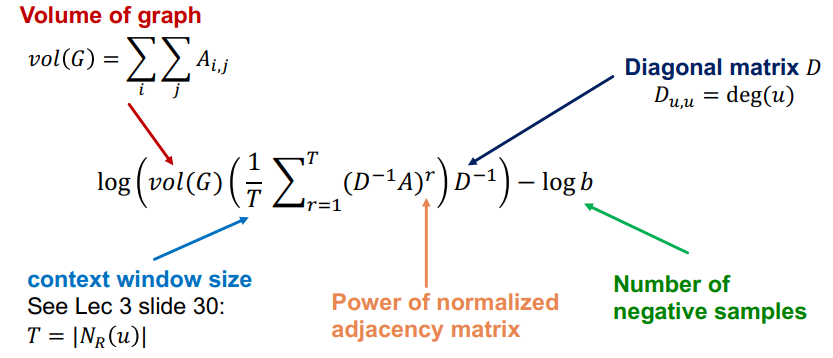
이때 r은 랜덤워크에서 수행할 걸음수를 의미하고, T는 전체 윈도우 사이즈를 의미한다. 또한, D 행렬은 대각행렬로 각 노드의 degree가 element를 이루고 있다.
수업에서 자세히 설명하지 않아 관련 논문(Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec, WSDM 18)을 살펴봐야 자세한 증명을 알 수 있을 것 같다. 하지만 큰 개념은 결국 랜덤워크 역시 결국은 행렬분해를 통해 구성되어 있다는 점인 것 같다.

5. Limitation

지난 강의와 이번 강의에 걸쳐 어떻게 노드, 엣지, 그래프를 임베딩할 수 있는지 랜덤워크 기반의 방법론들을 배웠다. 기본적으로 다른 feature engineering 방법론들에 비해 다양한 그래프 요소들을 효과적으로 잡고 있지만, 분명한 한계점을 가지고 있는 것도 사실이다.

훈련 시 학습되지 못한 노드의 임베딩 벡터를 만들 수 없다.
기본적으로 랜덤워크 기반의 방법론들은 모두 Bog of Words의 개념을 차용하고 있어 똑같은 한계점을 가지고 있다. BoW가 Out of Bag 문제를 처리하는데 어려움을 겪듯이 랜덤워크 기반 방법론들도 학습 시 존재하지 않았던 노드를 임베딩하기 위해서는 전체 학습과정을 전부 다시 진행해야 한다.
구조적 유사도를 잘 잡아내지 못한다.

위와 같은 그래프 구조에서 1번 노드와 11번 노드는 비슷한 구조를 가지고 있다. 하지만 DeepWalk나 node2vec은 인접 노드의 임베딩 벡터를 이용해 최적화하기 때문에, 1번과 11번이 비슷한 구조를 가지고 있다는 것을 잘 잡아내지 못한다. 물론 Anonymous Walk의 경우 이를 잡아낼 수 있기는 하다.
노드, 엣지, 그래프의 변수들을 활용하지 못한다.
랜덤워크 방법론들은 결국 그래프의 구조적 정보만 활용하게 된다. 하지만 실제로 그래프는 노드, 엣지, 그래프에 수많은 변수를 가지고 있고, 이러한 정보들이 아주 중요할 수도 있다. 이를 랜덤워크 방법론에선 활용할 수 없다. 이를 개선한 방법론인 다음 수업에서 배울 GNN이 되겠다.