[CS224W] Lecture 5 - Message Passing and Node Classification

김재희·2021년 8월 9일

목록 보기

5/11

이번 수업에서 다룬 내용은 한 그래프에서 특정 노드들에 레이블에 매겨져 있을 때, 다른 노드들에 레이블을 매기는 방법에 대해 다루게 된다. 즉, 아래 그림과 같이 그래프 전체에서 일부 노드에 레이블이 있고, 나머지 노드에는 레이블이 없을 때, 이를 예측하는 방법론을 다룬다.

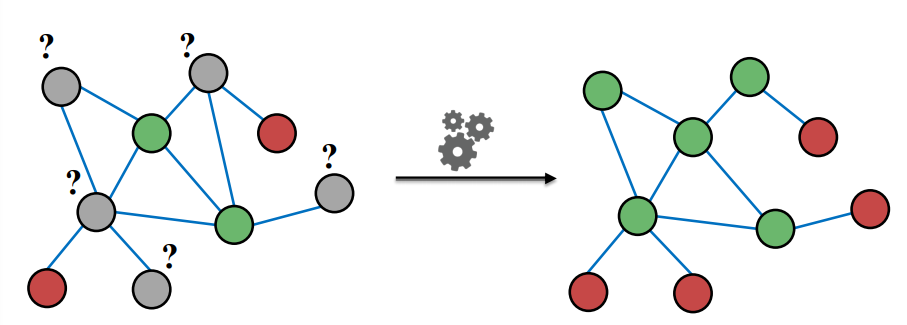
이를 Semi-supervised node classification이라 한다고 한다. 이미 레이블이 있는 정보와, 없는 구조를 학습하여 새로이 레이블을 예측하기 때문으로 보인다.

이를 Message Passing이라는 프레임 워크를 살펴보게 되는데, message passing 의 주요 개념은 상관관계(correlation)이다.
즉, 비슷한 노드 간에는 상관관계가 있을 것이기 때문에, 노드 간에 상관관계를 파악하여 이를 이용해 레이블을 예측하고자 한다. 여기서 반복적으로 레이블링의 작업이 발생하기 때문에, 이전 수업인 pagerank와 비슷한 점이 있다고 넘어가자.

1. Correlation

노드에서의 상관관계는 무엇을 의미하는 것일까?

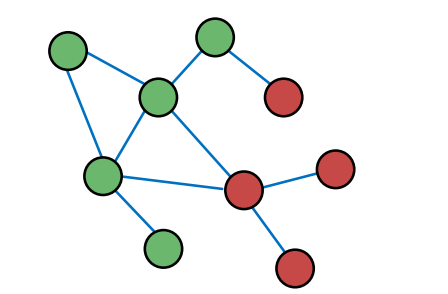
위의 그래프에서, 비슷한 노드(같은 레이블을 가지고 있는 노드)는 근처에 위치하는 것을 알 수 있다. 이와 같이, 노드 간의 관계를 파악하여, 서로 근접한 노드를 찾을 수 있다면, 거기에 비슷한 레이블을 매길 수 있을 것이다. 여기서 이제 어떻게 노드 간의 상관관계를 이끌어 낼 수 있을지 살펴보자.

노드 간의 상관관계는 Homophily, Influence 두 개념에 의해 정의되어진다. 두 개념 모두 사회과학 분야에서 social network를 분석하면서 쓰인 개념으로 보이는데, 하나씩 자세히 살펴보도록 하자.

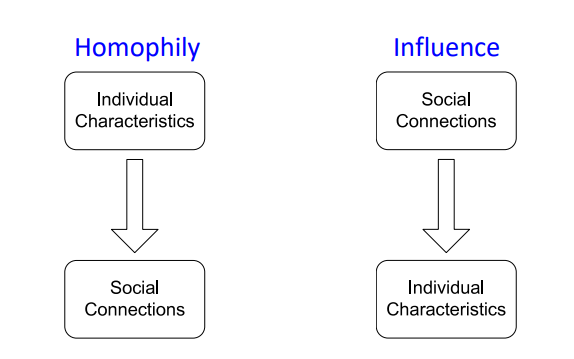
1-1. Homophily

개인의 특징은 나이, 성별, 직업, 취미, 거주지 등 다양한 요소가 있을 것이다. Homophily는 개인들이 비슷한 특징을 가지는 타인들과 서로 연결되고, 함께 행동하려고 한다는 개념이다. 예를 들어, 머신러닝 연구자들은 비슷한 학회를 동시에 참여하고, 비슷한 커뮤니티를 읽고 토론하게 되면서 자연스레 친분을 쌓게 된다. 또한, 가수들은 서로 같이 공연하고, 서로의 앨범을 들으면서 서로 사회적으로 연결되게 된다.

위의 그래프는 한 학교의 학생들을 나타낸 그래프인데, 학생 개인이 노드, 친분이 엣지로 표현되어 있다. 이때 노드의 레이블인 색은 각 학생의 관심사로 운동, 예술 등이 있다. 직관적으로 살펴보아도 알 수 있지만 총 4개의 작은 그룹으로 나누어질 수 있으며, 각 그룹은 비슷한 관심사를 가지는 학생들이 모여있는 것을 알 수 있다. 이를 Homophily라고 할 수 있을 것이다.

1-2. Influence

Influence는 사회적으로 연결된 개인 간에는 서로 영향을 주고 받으면서 비슷한 특징을 가지게 된다는 것을 의미한다. 예를 들어, 내가 1, 2학년 때는 경상계열 친구들과 친하게 지내면서, 경제, 사회, 제도 등에 관심을 가지고 해당 직군을 희망했다면, 3, 4학년이 되면서 통계나 수학, 컴퓨터 공학 친구들과 친하게 지내면서 ML, DL, 코딩 등에 관심을 가지고 해당 직군을 희망하게 된 것이 Influence 때문이라고 할 수 있을 것이다.

2. Motivation

전반적인 아이디어는 다음과 같다.

한 그래프 내에서 비슷한 노드는 가까이 위치하거나 직접 연결되어 있을 것이다.

이를 Guilt-by-association이라고 하는데, 노드 b가 아직 레이블이 없는 상태에서, 이웃노드 x가 1로 레이블 되어 있다면, 이웃노드 x와 가깝기 때문에 노드 b 역시 1로 레이블 될 가능성이 높다는 개념이다.

구체적인 예시로는 스팸 사이트들이 안전한 사이트와의 연결고리는 생성할 수 없기 때문에, 노출도와 신뢰도를 높이기 위해 서로 링크를 연결하는 경향이 있는데, 이를 이용해서 스팸 사이트 하나를 잡을 수 있다면, 서로 연결된 다른 스팸 사이트도 색출 할 수 있다고 한다.

이때, 노드 v의 분류에 이용하는 정보들은 다음과 같다.

노드 v의 변수들
노드 v의 이웃 노드들의 레이블
노드 v의 이웃 노드들의 변수들

실제로 이용하게 되는 입력값은 다음과 같다.

인접행렬 $A_{n \times n}$
레이블 벡터 $Y = \{0, 1\}^n$ $Y_v = 1, \; belongs \; to \; Class \; 1 \\ Y_v = 0 \; belongs \; to \; Class \; 0 \\$

목표는 다음과 같을 것이다.

아직 레이블이 없는 노드에 대해 레이블이 0 혹은 1일 확률을 계산하는 것.

이러한 방법론은 다양한 분야에 적용이 가능한데, 내가 관심이 있는 NLP에선 문서 분류 문제나, PoS 태깅 등에 활용되는 것으로 보인다.

3. Collective Classification

3-1. Overview

collective classification을 전반적으로 살펴보면 다음과 같다.

Intuition : 노드 간 상관관계를 이용해 서로 연결된 노드들을 동시에 분류하기

이때 1차 마르코프 연쇄를 사용한다. 즉, 노드 v의 레이블 $Y_v$ 를 예측하기 위해서는 이웃노드 $N_v$ 만 필요하다는 것이다. 2차 마르코프 연쇄를 사용할 경우 $N_v$ 의 이웃노드 역시 사용할 것이다. 1차 마르포크 연쇄를 사용할 경우 식은 다음과 같아질 것이다.

P(Y_v) =P(Y_v \mid N_v)

collective classification은 하나의 모델을 이용하거나 기존의 분류모델처럼 한번의 과정으로 구성되지 않고 총 세가지 과정으로 구성된다. 하나씩 살펴보자.

3-2. Local Classifier

최초로 레이블을 할당하기 위해 사용되는 분류기이다. 즉, 그래프에서 레이블이 없는 노드들에 대해 우선 노드를 생성해야 하기 때문에, 기존의 분류문제와 동일하게 구성된다. 이때 예측 과정은 각 노드의 변수만 사용하여 이미 레이블이 있는 노드로 학습하고, 레이블이 없는 노드로 예측하게 된다. 그래프의 구조적 정보가 사용되지 않는다는 점에 유의하자.

3-3. Relational Classifier

노드 간 상관관계를 파악하기 위해 이웃 노드의 레이블과 변수를 사용하는 분류기이다. 이를 통해 이웃 노드의 레이블과 변수와 현재 노드의 변수를 이용해 현재 노드의 레이블을 예측할 수 있다. 이때, 이웃노드의 정보가 사용되기 때문에, 그래프의 구조적 정보가 사용된다.

3-4. Collective Inference

Collective Classification은 한번의 예측으로 종료되지 않는 것이 핵심이다. 특정 조건을 만족할 때까지 각 노드에 대해 분류하고 레이블을 업데이트한다. 이때의 조건이란 더이상 레이블이 변하지 않거나, 정해진 횟수를 의미한다. 이때 동일한 변수를 가진 노드라 하더라도 그래프의 구조에 따라 최종 예측이 달라질 수 있다는 점을 유념하자.

4. Relational Classifiers

Probablistic Relational Classifier의 기본 아이디어는 다음과 같다.

노드 $v$의 레이블 확률 $Y_v$는 노드 $v$의 주변노드의 레이블 확률의 가중평균과 같다.

즉, 레이블이 없는 노드에 대해 이웃 노드들의 레이블 확률을 가중평균하여 예측하게 된다. 이진 분류문제라 가정하고, 모든 노드에 레이블 확률이 존재해야 하기 때문에, 레이블이 없는 노드는 0.5의 확률로 초기화하여 시작하게 된다.
업데이트는 반복적으로 진행되며, 모든 노드에 대해 수렴하거나 반복횟수에 도달할 경우 멈추게 된다.

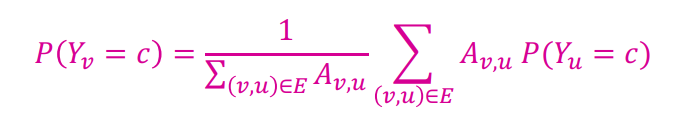
노드 $v$ 에 대한 확률을 계산하는 법은 위와 같다. 이때 행렬 A는 인접행렬에 해당한다. 즉, 주변의 이웃노드의 확률 $P(y_u = c)$ 를 평균하여 사용하되, 해당 이웃노드와 연결된 degree만큼 가중치, $A_{v, u}$ 를 주게 된다.

이때 두가지 문제점이 있다.

위 수식은 수렴이 보장되지 않는다.
모델이 노드의 변수를 활용하지 않는다.

이에 대해선 이후 모델을 통해 개선될 것이라 기대해보자.

4-1. Implementation

전체 과정을 살펴보면 다음과 같다.

Initializationz

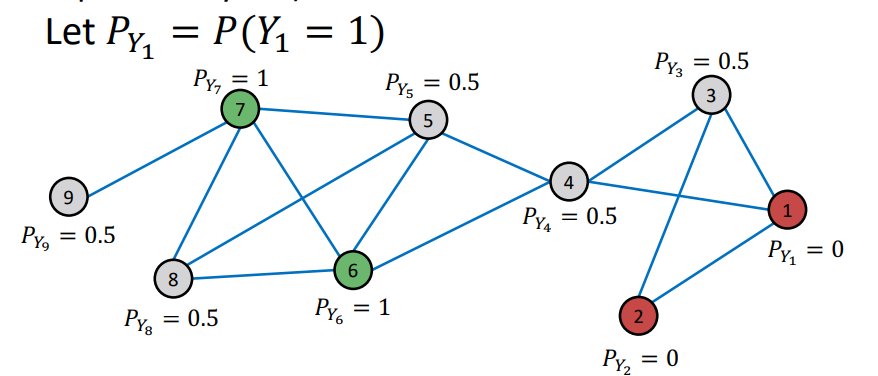
위 그래프에서 본래 레이블이 있는 노드는 녹색과 적색으로 표시가 되어 있다. 이에 대해 이진분류 문제이기 때문에, 녹색을 기준으로 확률을 계산하여, 녹색 노드는 1, 적색 노드는 0, 레이블이 없는 회색노드는 0.5로 초기화한다.
Update for the 1st Iteration

각 노드별로 이웃노드의 확률을 이용해 순차적으로 확률을 업데이트한다.
위 그래프의 경우 undirected이고 엣지가 각 노드 간 최대 하나만 존재하기 때문에 단순 평균을 통해 새로운 확률을 계산하게 된다.

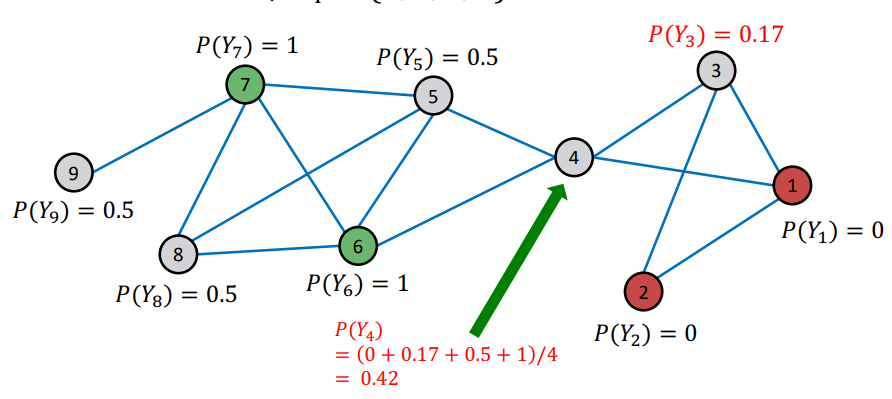
위에서 업데이트된 3번 노드의 확률을 이용해 4번 노드 역시 업데이트하게 된다. 즉, 노드를 업데이트하는 순서에 따라 계산이 조금씩 달라지게 된다.

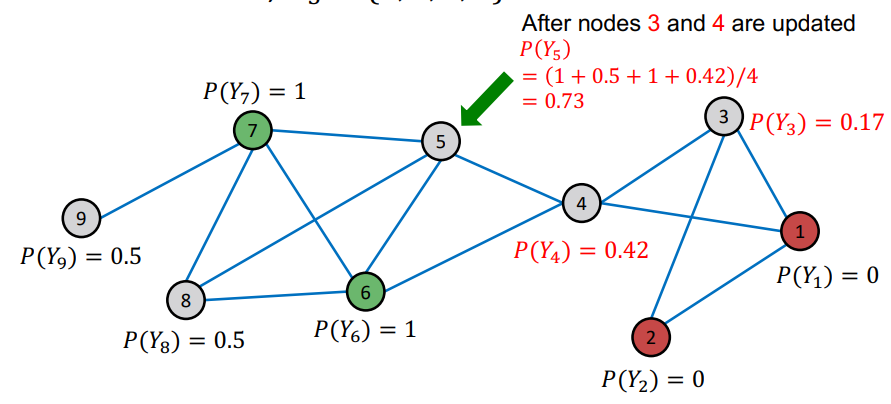
3, 4번 노드를 업데이트하고 나서 5번 노드를 업데이트한다. 이때 역시 업데이트된 4번 노드의 확률을 이용하게 된다.

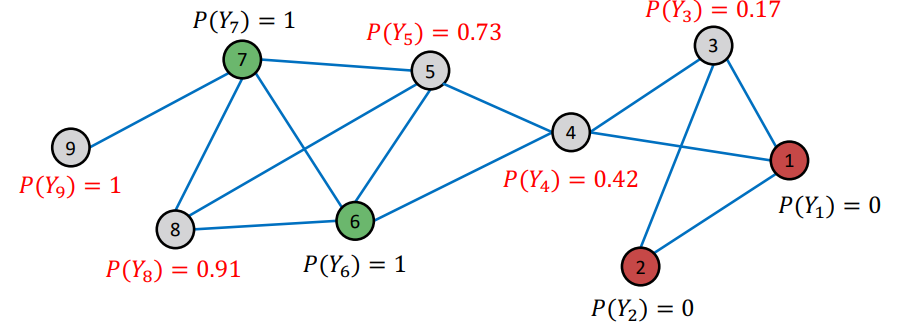
첫번째 이터가 종료된 후의 모습니다. 9번 노드의 경우 녹색 노드만 연결되어 있기 때문에 확률이 1로 고정된 모습을 보이고 있다. 이외에 8번 노드 역시 주변에 녹색 노드 2개, 확률이 높은 노드(5번) 한개가 이웃노드이기 때문에 확률이 높은 것을 볼 수 있다. 하지만 4번 노드의 경우 녹색 노드와 적색 노드 각각 하나씩 연결되어 있고, 녹색과 가까운 노드와 적색과 가까운 노드 하나씩 연결되어 있어 0.5에 가까운 확률을 보이고 있다.

Convergence

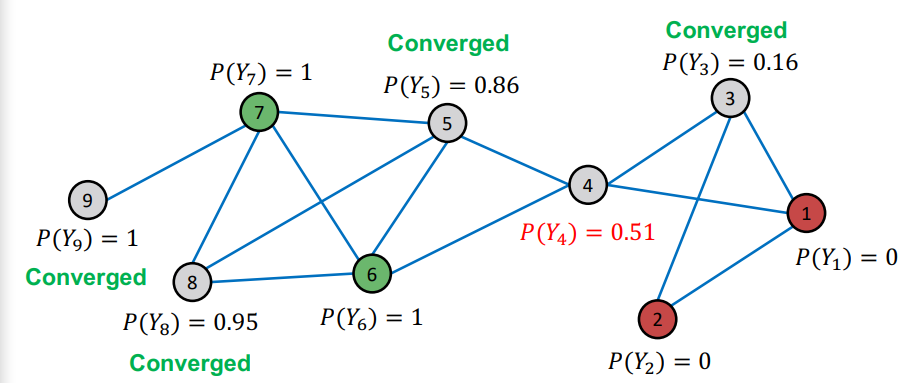
몇 번의 이터가 지나자 모든 확률값이 수렴하고 있는 모습을 보여 종료되었다.

이를 이전에 배웠던 개념과 연결지어 생각하자면, Influence가 녹아있는 모델이라고 할 수 있겠다. 가까운 노드의 영향을 받아 이웃 노드와 비슷한 레이블 분포를 가지도록 업데이트하고 있기 때문이다. 그 결과 8번 노드는 이웃노드가 녹색일 확률이 높으니 해당 분포와 비슷해지고, 4번 노드는 이웃노드로 녹색과 적색에 가까운 노드들이 모두 있어 0.5에 가까운 확률을 가지게 되었다.

Relational Classification은 그래프의 구조적 정보를 일부 활용하고, 노드 레이블은 활용하지만, 노드의 변수를 활용하지 못한다는 단점이 크게 작용한다. 결국 주어진 정보를 최대한 활용하지 못하는 머신러닝 모델은 부족한 점이 많은 모델일 뿐이다.

5. Iterative Classification

Relational Classifier는 노드의 변수를 활용하지 않는 것이 단점이라고 했다. Iterative Classifier는 노드의 변수를 활용하여 이를 개선했다. 핵심 아이디어는 다음과 같다.

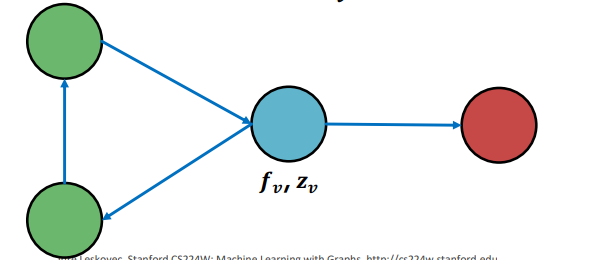
노드 v를 분류할 때, 노드의 변수 $f_v$ 를 이웃노드 집합 $N_v$ 의 레이블 $Z_v$ 와 함께 사용하자.

전반적인 구조는 다음과 같다.

Input : 그래프.
$f_v$ : 노드 $v$ 의 변수 벡터
일부 노드는 레이블 $Y_v$ 가 있음
Task : 레이블이 없는 노드에 대해 레이블을 예측할 것.
두 분류기를 통해 이를 달성
$\phi_1(f_v)$ : 노드 $v$ 의 변수 $f_v$ 를 이용해 레이블 예측하는 모델
$\phi_2(f_v, z_v)$ : 노드 $v$ 의 변수 $f_v$ 와 이웃 노드의 레이블에 대한 기술 통계벡터 $z_v$ 를 이용하여 레이블을 예측하는 모델

5-1. Computiong $z_v$

이웃 노드의 레이블에 대한 기술 통계 벡터 $z_v$ 는 다음과 같이 만들어진다.

위와 같은 그래프에서 청색 노드에 대한 $z_v$ 는 이웃 노드의 색의 count 분포나 존재 유무 분포, 비율 분포 등을 사용해 만들 수 있다.

count 분포 : [녹색 노드의 수, 적색 노드의 수] = [2, 1]
존재 유무 분포 : [녹색 노드 존재 여부, 적색 노드 존재 여부] = [1, 1]
비율 분포 : [녹색 노드 비율, 적색 노드 비율] = [ ${2 \over 3}, {1 \over 3}$ ]

두 분류기를 이용하여 학습과 예측 과정이 조금 복잡한데 크게 두 단계로 나눌 수 있다.

5-2. Train & Inference

5-2-1. Train

학습 데이터의 경우에 모든 노드에 레이블이 달려있다고 간주한다.
1. $\phi_1(f_v)$ : $f_v$ 를 이용해 $Y_v$ 를 예측한다.
2. $\phi_2(f_v, z_v)$ : $f_v$ 와 $z_v$ 를 이용해 $Y_v$ 를 예측한다. 이때, $z_v$ 는 실제 레이블을 이용해 구성한다.

5-2-2. Inference

테스트 데이터의 경우엔 일부 노드에만 레이블이 달려있다고 간주한다. 혹은 레이블이 아예 없을 수도 있다고 간주한다.

이때 $\phi_1(f_v)$ 는 $f_v$ 가 변하지 않기 때문에 초기에 한번만 계산하여 $Y_v$ 를 예측하여 준다. 이를 통해 모든 노드에 $Y_v$ 가 할당된다.

모든 노드에 $Y_v$ 가 할당된 후 다음과 같은 과정을 수렴하거나 최대반복횟수에 도달할 때까지 반복한다.
1. 새로운 $Y_v$ 에 맞추어 $z_u$ 를 업데이트한다. ( $u \in N_v$ )
2. 새로운 $z_u$ 에 맞추어 $Y_z = \phi_2(f_v, z_v)$ 를 업데이트한다.

5-3. Implementation

예시를 통해 전체 과정을 한번 살펴보자.

Web Page Classification

Input : 웹페이지 그래프
Node : 웹페이지
Edge : 웹페이지 간 하이퍼링크(Directed Edge)
Node Features : 웹페이지 정보(TF-IDF 등의 토큰 정보, 여기선 2차원 벡터로 표현)
Task : 각 웹페이지의 주제 예측

5-3-1. Baseline

학습데이터를 이용해

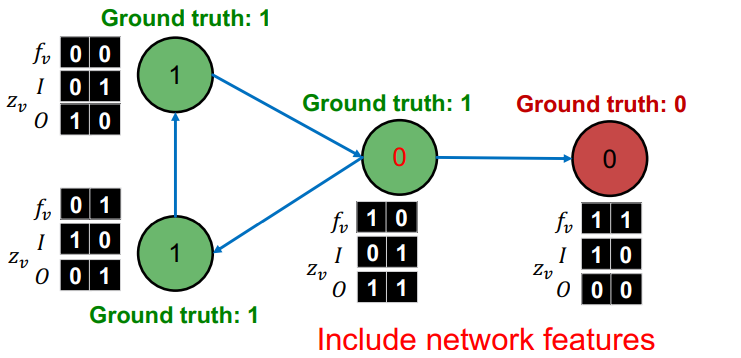
각 노드는 다음과 같은 세가지 벡터를 가지게 된다.

$f_v$ : 변수 벡터 (TF-IDF 등)
$I$ : incoming neighbor 레이블에 대한 기술 통계치 벡터([0인 이웃노드 유무, 1인 이웃노드 유무])
$O$ : outgoing neighbor 레이블에 대한 기술 통계치 벡터([0인 이웃노드 유무, 1인 이웃노드 유무])

5-3-2. Train & Test

Train : 각기 다른 훈련 데이터로 $\phi_1, \phi_2$ 에 해당하는 모델을 학습시킨다. 이때 $\phi_1$ 은 노드의 변수와 레이블 간의 관계를 파악하게 된다. $\phi_2$ 는 이웃 노드 레이블과 현재 노드의 변수와 레이블 간의 관계를 파악하게 된다.

위의 그림에서 녹색 원이 $\phi_1$ 이 학습에 사용하는 정보이고, 적색 원이 $\phi_2$ 가 학습에 사용하는 정보이다.
Test :
우선 $\phi_1$ 을 이용해 레이블이 없는 테스트 데이터의 노드에 대해 레이블을 부여한다.

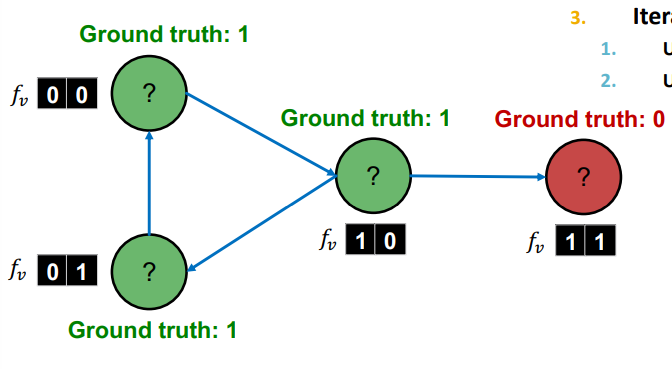
$\phi_1$ 이 부여한 레이블을 이용해 $z_v$ 를 업데이트한다.

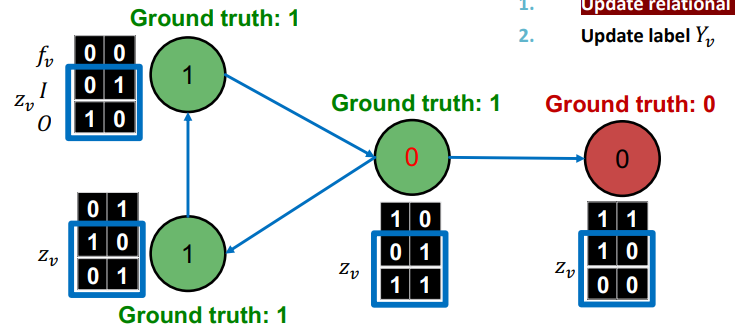
$\phi_2$ 가 레이블을 예측한다.

$\phi_2$ 에 의해 레이블이 변화했으므로, 다시 $z_v$ 를 업데이트한다.

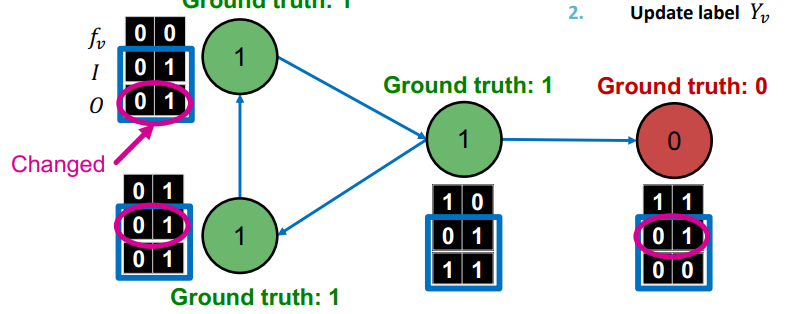
$z_v$ 가 업데이트 되었으므로 $\phi_2$ 가 레이블을 예측한다.

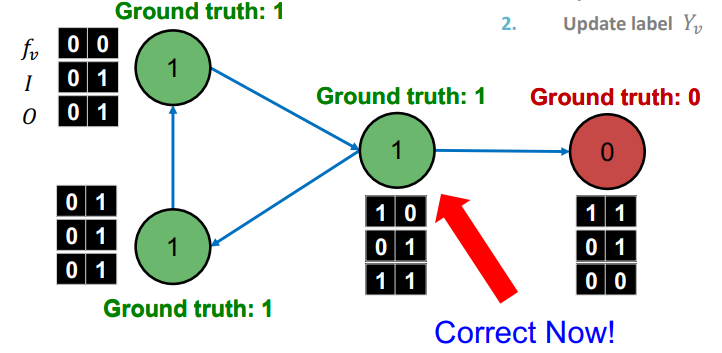
$\phi_2$ 를 통한 예측과 $z_v$ 에 대한 업데이트를 종료조건에 도달할 때까지 반복한다.

6. Loopy Belief Propagation

본론으로 들어가기에 앞서 앞에서 다뤘던 내용을 다시 짚어보자. 각 노드는 이웃 노드의 확률의 가중평균을 자신의 새로운 확률로 삼고 있다. 혹은 각 노드는 이웃 노드의 레이블을 활용해 자신의 새로운 확률을 계산하게 된다. 즉, 이웃노드의 정보가 각각의 노드에서 사용되고 있는 것이다.

이것을 각 노드는 이웃노드에게 Belief를 전달받는다고 할 수 있다. 즉 이웃 노드의 belief를 받아 자신의 belief를 생성한다. 다르게 말하면, 모델은 각 노드에 대해 매 이터마다 belief를 가지고 있고, 이웃 노드의 belief를 이용해 각 노드의 belief를 업데이트하고 있다.

그렇다면 왜 굳이 바로 이웃노드에서만 belief를 받아야 할까. 좀 더 먼 노드의 belief도 중요하게 작동하지 않을까? 왜냐하면 결국 이터레이션을 반복하여 이웃노드의 belief를 받게 된다면, 해당 belief는 이웃노드의 이웃노드의 belief가 섞여있는 상태기 때문에, 이터레이션을 반복한다는 것은 자신의 이웃노드의 이웃노드의 이웃노드의 .... belief를 받고 있는 것이기 때문이다. 이를 역으로 생각하여 belief가 그래프에 직접 흐르도록 알고리즘을 구성한 것이 loopy belief propagationdl 된다.

6-1. Basic

위와 같이 가장 단순한 그래프의 형태를 생각해보자. 우리가 원하는 것은 그래프의 노드 수를 계산하고자 한다. 이때 belief는 각 이터마다 이웃노드로만 전달될 수 있다. 이때 알고리즘은 다음과 같을 것이다.

노드의 순서를 정한다.
1에서 정한 순서에 따라 엣지의 방향을 정한다.
i번째 노드에 대해 다음을 시행한다.
i-1 노드에서 belief(이전까지 지나온 노드의 수)를 받는다.
belief에 1(자신에 대한 count)을 더한다.
i+1 노드로 belief를 전달한다.

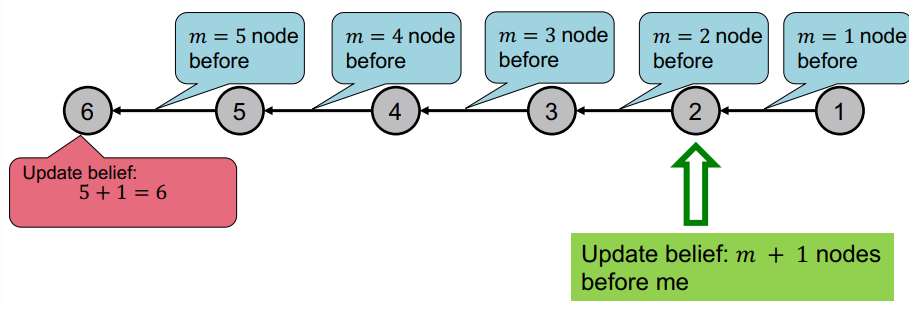
즉 위와 같은 상황이 될 것이다.

조금 더 복잡하게 아래와 같은 트리 구조에서 생각해보자. 트리는 parent와 child로 구성되어 있기 때문에, 전체 노드의 수를 세기 위해서 child에서 parent 방향으로 belief가 흐르면 될 것이다.

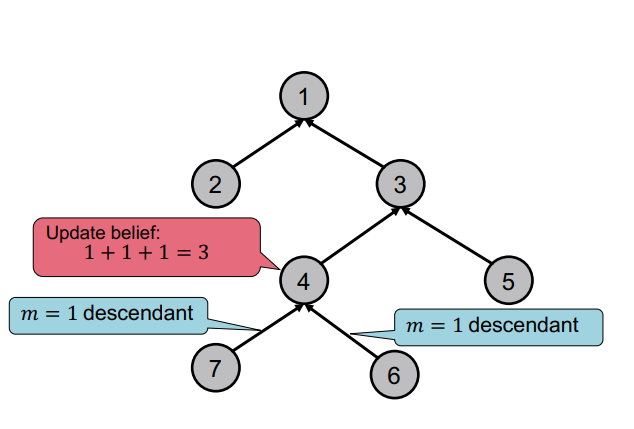
이때 위의 그림과 같이 parent 노드는 자신의 child 노드의 belief를 받아 종합하는 일종의 계산을 수행한 수 자신의 parent 노드로 belief를 넘겨주게 된다.

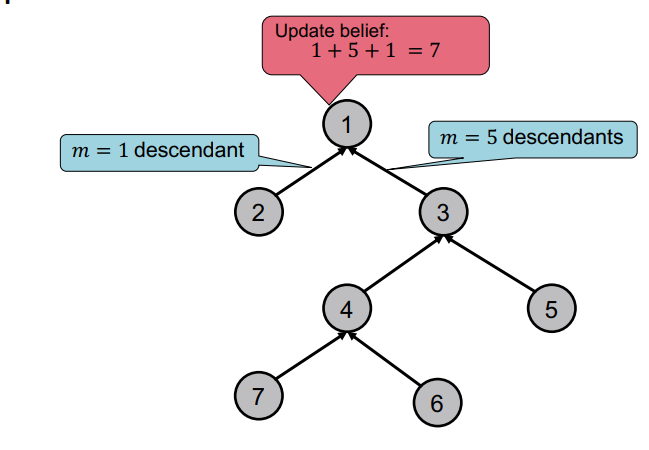
이를 통해 최종적으로 root 노드에서 전체 노드의 수를 구할 수 있을 것이다.

하지만 실제로 count를 belief로 간주하고 이웃 노드에 전달하지 않을 것이다. 실제로 알고리즘이 어떻게 되어 있는지 살펴보자.

6-2. Notation

$\psi$ (Label-Label Potential Matrix) : $\psi$ 는 각 노드가 이웃노드의 클래스에 대한 영향력을 행렬로 표현한 것이다. 예를 들어 $\psi(Y_i, Y_j)$ 는 이웃 노드 i의 레이블이 $Y_i$ 일 때, 노드 j가 $Y_j$ 레이블에 속할 확률의 비중이다.
$\phi$ (Prior Belief) : 노드 i가 $Y_i$ 에 속할 확률이다.
$m_{i \to j}(Y_j)$ : i의 메세지가 j로 전달되는 것을 의미하는데, i가 이웃 노드로 부터 받은 belief와 자신의 정보를 종합해 j의 레이블을 believe하는 것을 의미한다.
$L$ : 모든 레이블을 포함하는 집합

6-3. Algorithms

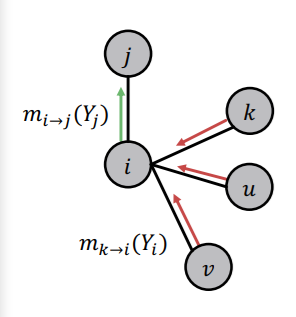
1. 가장 처음에는 모든 노드의 메세지를 1로 초기화한다.
2. 이후 다음과 같이 모든 노드에 대해 다음 노드로 메세지를 전달하는 과정을 반복한다.

이때 수식을 설명해보자면, 가장 앞의 분홍색 부분은 현재 노드 i의 모든 레이블의 가능성에 대해 반복하여 더한다는 의미이다.
녹색 부분은 label-label potential로서, i노드의 각 레이블마다 j노드가 $Y_j$ 레이블을 가질 확률을 계산하게 된다. 적색 부분은 Prior로서 i노드가 $Y_i$ 레이블을 가질 확률을 계산하게 된다. 청색 부분은 i 노드가 메세지를 넘겨받는 이웃 노드에서 i 노드가 $Y_i$ 레이블일 belief를 넘겨 받는 부분이다.

만약 위의 과정이 충분히 반복되어 수렴한다면 다음과 같이 실제 확률이 계산되게 된다.

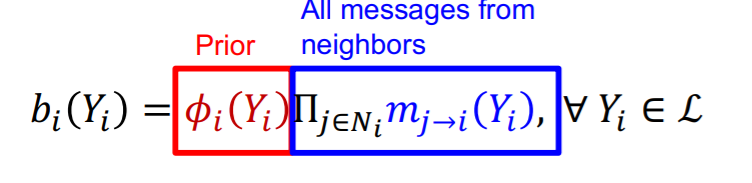
즉, Prior 확률에 belief를 모두 곱하여 준다.

6-4. A graph wih Cycle

지금까지 이야기한 그래프들은 순환하는 구조를 가지고 있지 않아 메세지를 전달할 순서를 정하는데 문제가 없었다. 하지만 순환하는 구조를 가지는 그래프의 경우에는 단순하게 노드의 순서를 정해서 메세지를 전달하도록 만들 수 없다. 그에 대해 자세히 살펴보자.

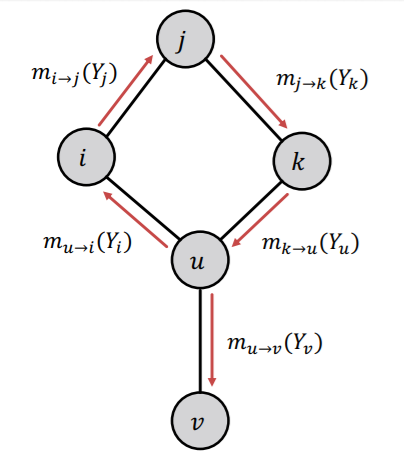
만약 위와 같은 그래프가 있고, 위와 같은 순서로 메세지를 주고 받는다고 생각해보자. u 노드는 k에게 메세지를 받는 것처럼 보이지만, 실제로는 자기 자신의 메세지마저 받고 있는 상황이다. 즉, 더이사 모든 노드가 독립적이지 않고, 의존성이 생긴다. 순서가 반대로 트리와 같이 j가 i, k로 메세지를 전달하고, i, k가 u로 메세지를 전달한다면, j의 메세지는 u에게 중복되어 두 번 전달되는 문제가 생긴다.

이렇게 되면 알고리즘이 크게 문제가 생기는 것 같지만, 실제 적용해보니 그렇지 않다고 한다. 실제 그래프들은 무척 크고, 거기에 순환하는 cycle 구조는 그렇게 큰 부분을 차지하지 않는데 반면, 전체 구조는 매우 복잡하기 때문에 Loopy BP 알고리즘이 잘 작동한다고 한다.

6-5. Advantages & Challenges

Advantages:

코딩이 쉽고, 병렬화가 가능하다.
어떠한 그래프 모델이더라도, potential matrix를 구성할 수 있으므로 범용적이다.

Challenges:
수렴이 보장되지 않아 언제 멈춰야 할지 모른다.
cycle 구조로 인해 종종 적은 이터만 돌리기도 한다.

참고

CS224W 강의
CW224W 강의자료

김재희

이전 포스트

[CS224W] Lecture 4 - PageRank

다음 포스트