[CS224W] Lecture 6 - Graph Neural Network1

김재희·2021년 8월 12일

CS224W

목록 보기

6/11

0. Recap

앞서 이야기한 내용들을 잠깐 정리하고 시작하도록 하자.

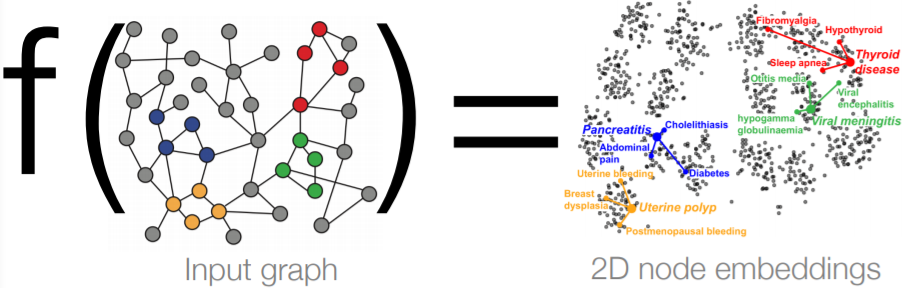
우리가 노드 임베딩을 통해 이루고자 한 것은 노드들을 임의의 d차원 벡터로 나타내려고 한 것이다. 이때, 잘 임베딩한다는 것의 정의를 다음과 같이 내렸다.

그래프 내에서 유사한 두 노드 $u, v$ 가 인코더를 통과한 두 벡터 $z_u, z_v$ 가 될 때, d 차원의 임베딩 공간에서도 두 벡터 $z_u, z_v$ 가 비슷한 공간에 위치할 것.

이때 우리는 그래프만 가지고 있고, 정의내려야 할 것이 3가지였다.

그래프에서의 유사도 정의
인코더 함수
임베딩 공간에서의 유사도 정의

그래프에서의 유사도는 랜덤워크나 딥워크 등을 통해 정의해봤고, 임베딩 공간에서의 유사도는 두 벡터의 내적으로 간주했다. 그리고 이를 디코더라고 부르기도 했다.

인코더 함수의 경우 Shallow Encoding을 통해 구현했는데, 이때 Look-up을 사용했다. Look-up이 랜덤워크 등과 결합하여 노드 임베딩을 수행했다고 할 수 있다.

하지만 Shllow Encoder은 몇가지 문제점이 있다.

$O(\lvert V \rvert)$ 의 파라미터가 필요하다.
각 노드 별로 개별적인 임베딩 벡터를 가지다 보니, 노드의 수가 기하급수적으로 늘어날 경우 파라미터의 수가 기하급수적으로 늘어나게 된다.
Transductive하다.
즉, 학습 시 사용되지 않은 노드는 Look-up table에 존재하지 않기 때문에 inference 과정에서 사용할 수 없었다.
노드의 변수들이 사용되지 않는다.
우리가 지금까지 배운 방법들은 대부분이 그래프의 구조적 정보만 활용하여 임베딩하였다.

1. Deep Graph Encoders

그래서 오늘 배울 것은 GNN이라 불리는 deep한 방법론들을 배워볼 것이다. 이때 사용할 노드의 유사도는 랜덤워크나 딥워크와 같이 이전에 사용한 노드의 유사도 개념과 동일한 것을 사용할 것이다. 다만 달라지는 것은 encoder의 구조이다.

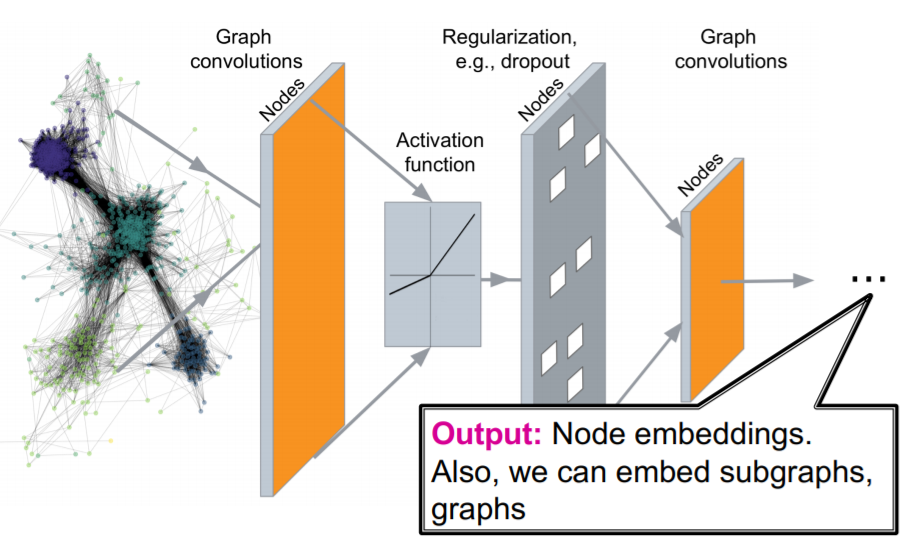
이제는 단순히 look-up만 하는 것이 아니라, cnn, rnn, dnn 등의 딥러닝 방법론들을 차용하여 인코더를 구성하게 된다. 즉, 인코더의 레이어가 깊어질 것이다.

이를 통해 GNN은 다음과 같은 여러 태스크를 수행할 수 있다.

Node classification
Link prediction
Community detection
Network similarity

1-1. Differences

그렇다면 기존의 DL 방법론과의 차이점은 무엇일까? 이미 이미지, 음성, 텍스트 등을 다루는 딥러닝 모델들이 많이 있는데, 무엇이 GNN을 다르게 할까?

무엇보다 그래프가 훨씬 복잡하다는 점이 다르다.
이미지는 격자 형태의 2d 혹은 3d 형태의 데이터고, 텍스트는 단방향의 선형 그래프 구조를 가지고 있다. 즉, 이미지는 주변의 local 정보들이 중요하게 작용하고, text는 이전 시점의 정보들이 중요하게 작용한다. 이것 외에 크게 다른 것은 없다.

하지만 그래프는 local의 개념이 불분명하고, 정해진 노드의 순서도 없으며, 위상적 형태이기 때문에 뒤집거나, 회전시켜도 변하지 않는다. 심지어 서로 멀어보이는 노드도 실제로는 2개의 경로로만 연결된 아주 가까운 노드일 수 있다.

2. Background

2-1. Notation

$V$ : vertex set, 노드 집합
$A$ : adjacency matrix, 인접 행렬
$v$ : $V$ 의 어떤 한 노드
$N(v)$ : 노드 v의 이웃노드 집합
$X \in R^{m \times \rvert V\lvert}$ 노드 변수들
이때의 노드 변수란 사용자 프로필이나 이미지, 작성한 텍스트, 유전자 정보, 유전자 역할 정보 등이 될 수 있다. 만약 변수가 없을 경우에도 흔히 노드 id를 의미하는 indicator vectors나 항수 벡터를 사용하기도 한다.

2-2. DNN

가장 나이브한 접근방법은 DNN을 접목하는 것일거다.

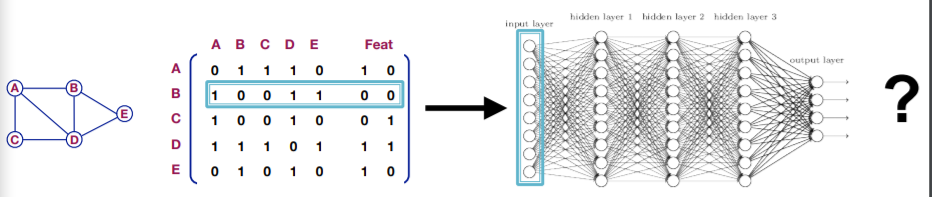
이때 입력 벡터는 위에서 보이는 것과 같이 인접행렬에서 해당 노드의 row 벡터로 해당 벡터와 이웃하는 노드의 one hot vector와 해당 노드의 변수이다. 하지만 이렇게 모델을 구성하면 몇가지 문제가 발생한다.

$O(\lvert V \rvert)$ 의 파라미터가 필요하다. 즉, 인접행렬의 column 수만큼은 입력값과 hidden layer를 연결하는 파라미터가 필요한데, 이러면 또 파라미터가 너무 많아져 과적합이 발생할 우려가 있다.
그래프가 다른 크기를 가질 경우 적용할 수 없다.
만약 전체 노드의 수가 10개 짜리인 그래프로 학습한 모델이 있다고 하자. 이 모델은 입력값으로 크기가 10인 벡터를 받는다. 하지만 그래프의 노드 수가 20인 그래프가 있다면, 해당 모델을 통한 분석이 불가능해진다.
노드 순서에 민감하다.
우리는 결국 그래프를 분석하고자 하는 것인데, SGD에 따라 어떤 노드를 먼저 입력값으로 받는지가 중요한 문제가 된다 결국 먼저 입력값으로 들어온 노드에 맞추어 그래디언트를 따라 흐르고 다음 입력값을 고려하게 되기 때문이다.

2-3. Convolutional Networks

CNN을 그대로 그래프에 적용하는 것 역시 문제가 발생한다. 그래프 이미지를 입력값으로 하는 모델을 생각하면,

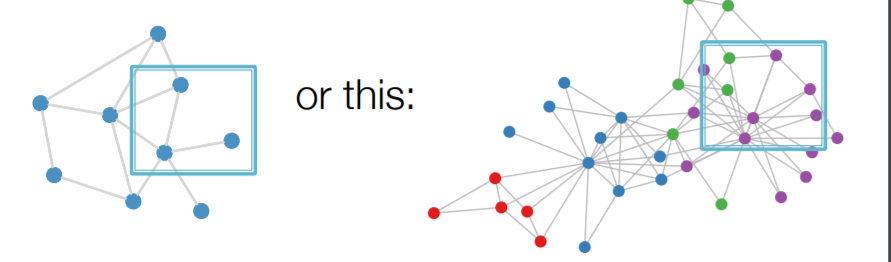
위와 같이 똑같은 window size에 들어오는 노드의 갯수가 슬라이딩하면서 큰 차이가 나버린다. 즉, 각 슬라이딩 위도우마다 제각기 다른 이미지가 들어오게 되는 것이다. 이는 이미지는 고정되 크기임에 반해, 그래프는 고정된 크기의 그리드로 되어 있지 않아 발생하는 문제이다.

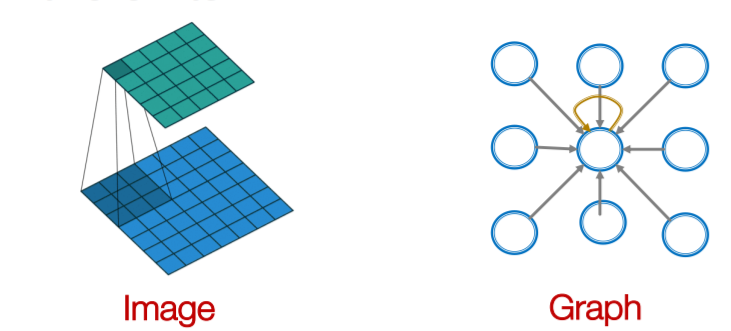
이를 개선하고자 위와 같이 생각해보자. CNN에서 한 레이어가 하는 일은, 기준이 되는 픽셀을 중심으로 상하좌우 대각선의 픽셀에서 정보를 받아 종합하고, 이를 일종의 연산을 통해 하나의 픽셀을 내밷는다. 이는 그래프에서 한 노드를 중심으로 이웃노드에서 메세지를 받아 하나의 노드로 메세지를 종합하고, 연산하여 현재 노드의 메세지를 만드는 일과 비슷하다고 할 수 있다. 즉 이미지의 Locality를 그래프의 메세지 개념으로 연결해볼 수 있지 않을까?

3. Graph Convolutional Networks

CNN의 아이디어를 빌려 그래프에 접목한 GCN에 대해 알아보도록 하자.

3-1. Steps

GCN은 기존의 딥러닝 모델과 다른 과정을 가지고 있다. 기존의 딥러닝 모델은 고정되 모델 구조에 대해 여러 case의 데이터를 입력받아 순전파, 손실함수 계산, 역전파의 과정을 통해 최적화하게 된다. 하지만 GCN은 다음과 같은 두 과정으로 구성되어 있다(손실함수 계산이나 역전파는 동일하다.).

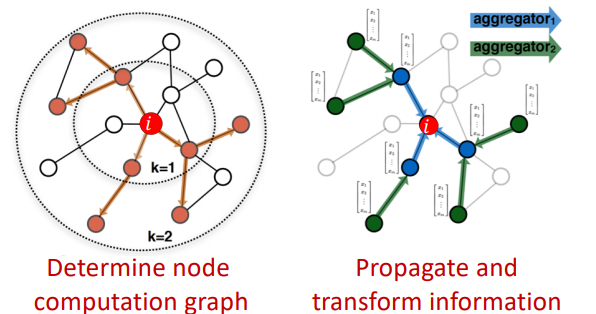
1. 각 노드 별 계산 그래프 생성
2. 각 노드 별 계산 그래프에 따라 순전파

이를 자세히 살펴보자.

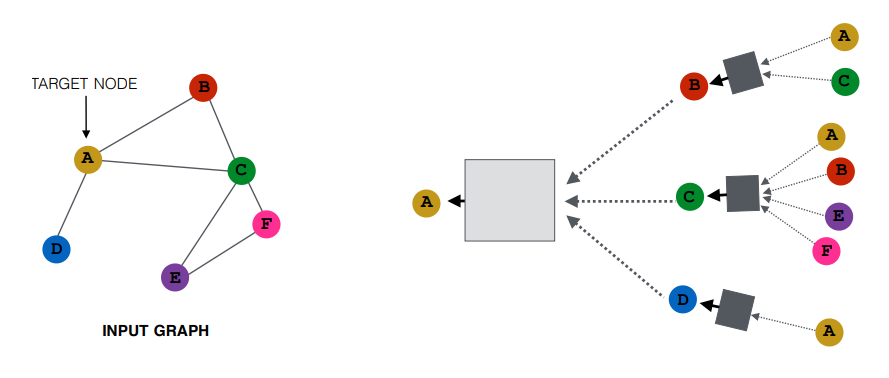
왼쪽과 같은 그래프에서 A 노드에 대해 2 hop node까지 계산 그래프를 생성하면 오른쪽 그림과 같다. 즉, A는 이웃 노드 D, B, C로부터 정보를 받고, 해당 노드들의 각자의 이웃노드에서 정보를 받는다. 이를 계산그래프로 풀어 A 노드에 대한 하나의 모델이 만들어지게 된다. 이때 정보의 흐름에 따라 순서를 매겨보면 계산 그래프에서 오른쪽에서 왼쪽으로 정보가 흘러야 한다. 오른쪽 가장 위를 예를 들어보면, A와 C 노드에서 정보가 B로 흘러가야 한다. 이때의 과정은 A와 C 노드에 해당하는 임베딩 벡터를 입력으로 하여 정보가 합쳐져서 연산이 이루어져 레이어를 통과한다. 이렇게 B를 향해 모아진 정보는 기존의 B의 임베딩 벡터와 연산을 거쳐 두번째 레이어의 B 노드에 대한 임베딩 벡터로 사용된다. 즉, 첫번째 레이어의 B 노드의 임베딩 벡터와 두번째 B 노드의 임베딩 벡터는 달라진다.

위 그림에서 생성되는 모든 계산 그래프를 표시하면 위와 같다. 그리고 각각의 계산 그래프는 각각의 모델 구조를 가지고 있게 된다. 각 노드마다 가지는 그래프 구조가 달라지기 때문에 천차만별의 모습을 하고 잇는 것을 알 수 있다. 파란색 D 노드의 경우 A노드만 이웃노드로 가지기 때문에 매우 좁은 형태를 가지고 있고, 녹색 C 노드는 매우 넓은 형태를 가지고 있는 것을 알 수 있다. E와 F 노드의 경우 동일한 계산 그래프를 가지고 있다. 다른 말로 동일한 모델을 통해 처리될 수 있다.

이때 레이어는 깊지 않다고 한다. 아무래도 모든 노드에 대해 각기 다른 계산 그래프가 생성되다 보니 깊어지기 힘든 것으로 보인다. 또한 k번째 레이어의 임베딩 벡터는 곧 k hop 멀리 떨어진 노드부터 정보가 모아져 온 것으로 이해할 수도 있다.

3-2. Neighborhood Aggregation

그렇다면 어떻게 각 레이어는 이웃노드의 정보(belief)를 이번 노드의 정보와 모아 다음 노드로 전달할 정보(belief)를 만드는 걸까?

우선 정보를 합치는 과정은 한 레이어의 입력값의 위치에 무관한 연산이어야 한다.

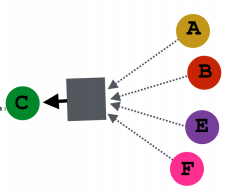
즉, C 노드의 이웃노드 A, B, E, F는 모두 동등한 이웃노드이다. 위 그림과 같이 A 노드가 위에 있지 않고, 맨 아래에 있어도 동일한 구조이다. 그러므로 이웃노드가 계산 그래프에서 어디에 위치하든 관계없이 동등한 연산이 이루어져야 한다.

이에 가장 적합하면서 단순한 연산은 평균/합일 것이다. 즉, 각 이웃 노드의 임베딩 벡터와 현재 노드의 임베딩 벡터를 차원 별로 더하거나 평균을 내면 다음 레이어로 전달할 정보의 형태가 될 수 있을 것이다. 자세한 전체 수식은 다음과 같다.

h_v^0 = x_v\\ h^{(l + 1)}_v = \sigma (W_l \sum_{u \in N(v)} {h^{(l)} \over {\lvert N(v) \rvert}} + B_lh_v^{(l)}), \forall l \in \{0, \dots , L -1\}\\ z_v = h_v^{(L)}\\

전체 레이어 수를 $L$ 이라고 할 때,
첫번째 히든 레이어의 입력값은 각 노드의 변수벡터 혹은 임베딩 벡터이다.
두번째 히든 레이어부터 마지막 히든 레이어까지 입력값은 각 레이어의 이웃노드의 벡터의 평균( ${h^{(l)} \over {\lvert N(v) \rvert}}$ )과 이전 레이어의 해당 노드( $v$ )의 벡터( $h_v^{(l)}$ )를 선형 변환 후 결합하여 활성화 함수를 통과한 값이 된다.

이때 학습에 사용되는 파라미터는 $W_l, B_l$ 두 행렬에 담겨 있는 것이 전부이다. 즉, 이전에는 모두 다른 계산 그래프를 가진다고 이야기했지만, 결국은 모든 계산그래프가 평균/합 aggregation을 거쳐 각 레이어에 동일한 입력값의 형태를 띄게 되므로, 모든 계산그래프는 동일한 가중치를 공유하는 형태가 된 것이다.

3-3. Matrix Formulation

실제 그래프 구조는 인접행렬 등의 행렬로 표현되기 때문에, 연산 역시 행렬단위로 이루어질 수밖에 없다. 이에 대해 자세히 살펴보자.

$H^{(l)} = [h^{(l)}_1, \dots , h^{(l)}_{\lvert V \rvert}]^T$ : l번째 레이어의 모든 노드에 대한 벡터를 concat하여 행렬 $H^{(l)}$ 로 나타낼 수 있다. 이때 shape은 (노드, 차원)이 될 것이다.
$\sum_{u \in N_v} h^{(l)}_v = A_{v,:}H^{(l)}$ : $H^{(l)}$ 을 이용하면 $v$ 노드의 모든 이웃 노드의 벡터를 쉽게 더할 수 있다. 식에 보이듯이, 인접행렬에서 $v$ 행은 노드 $v$ 의 이웃 노드에서만 1로 표시된 one hot vector이고, 이때의 벡터와 행렬의 연산은 결국 (1, 노드) x (노드, 차원) = (1, 차원)으로 모든 이웃 노드의 벡터의 합이 될 것이다.
$D_{v, v} = Deg(v) = \lvert N(v) \rvert$ : D 행렬을 대각행렬이고, 각 대각 성분은 $v$ 노드의 이웃노드의 수를 가지고 있다고 하자. 이를 이용하면 $D$ 행렬의 역행렬은 다음과 같은 대각성분을 가지게 된다. $D^{-1}_{v, v} = {1 \over \lvert N(v) \rvert}$ 즉, $v$ 노드의 이웃노드의 수의 역수가 된다.

위 세가지 요소를 조합하면 이웃노드의 평균을 구하는 과정을 아래와 같이 행렬로 표현할 수 있다.

\sum_{u \in N(v)} {h^{(l)} \over {\lvert N(v) \rvert}} = H^{(l + 1)} = D^-1AH^{(l)}

이제 식을 완전히 정리하면 아래와 같이 된다.

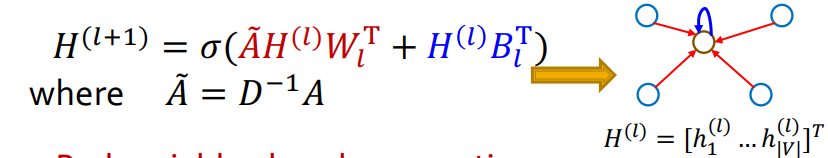
아래 식에서 적색 부분은 이웃 노드의 정보를 모으는 부분이고, 청색 부분은 본인 노드의 정보를 변형하는 과정이다. 위 식에서 하나 더 집중할 부분은 $\tilde{A}$ 가 매우 sparse한 행렬이기 때문에, sparse matrix multiplication을 도입하여 효과적인 연산이 가능할 것이라는 점이다.

또한, 위의 수식은 aggregation을 평균으로 정의했을 때 가능한 식이다. 만약 aggregatoin이 좀 더 복잡해진다면 이러한 행렬 형태로 표현할 수 없을 수도 있다.

3-4. Training

GNN의 학습과정을 이야기하기 전에, 위의 모델이 만드는 출력은 결국 $z_v$ 이다. 즉, 노드 $v$ 의 변수와 그래프 구조를 이용해 생성한 임베딩 벡터인 것이다. 이를 학습하기 위해서는 손실함수를 정의하고 이에 맞추어 최적화해야한다. 이때 지도학습과 비지도학습 모두 사용가능하다.

3-4-1. 비지도학습

비지도학습은 노드의 레이블이 없는 경우에 사용된다. 노드의 레이블 대신에 그래프의 구조 자체를 목표로 삼고 학습하게 되는 것이다.

즉, 그래프 구조에서 비슷한 노드 간에는 임베딩 공간에서도 비슷한 위치에 있을 것이라 가정한다. 그래프 구조에서의 유사도는 이전에 배웠던 랜덤워크나 행렬분해 등의 방법이 사용되고, 디코더로는 내적이 기본적으로 사용된다.

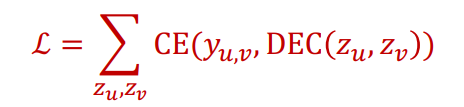
손실함수는 위와 같다. 여기서 $y_{u, v}$ 는 $u, v$ 노드가 유사할 경우 1, 아닐 경우 0을 나타낸다. 즉, 유사할 경우 디코더가 1을 계산하고, 유사하지 않을 경우 0을 계산하도록 GNN의 파라미터가 최적화된다.

3-4-2. 지도학습

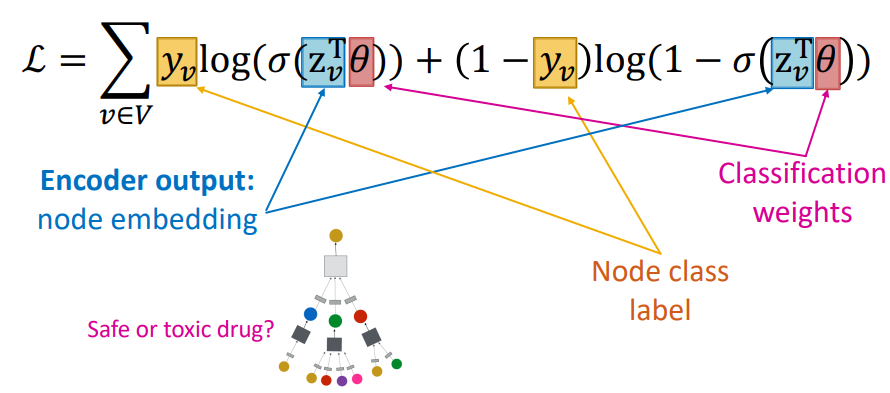
지도학습은 각 노드의 레이블을 예측하는 방식으로 손실함수를 구현하게 된다. 예를 들어 약제 간 상호작용 네트워크에서 약품 A의 독성유무를 레이블로 가지고 있다면, 아래와 같이 로짓회귀등의 입력값으로 $z_v$ 를 삼고 손실함수를 구현할 수 있다.

3-5. Model Design

전반적인 GNN 모델 구성은 다음과 같이 요약할 수 있다.

neighborhood aggregation function 정의
임베딩 벡터에 대한 손실함수 정의
노드 집합을 배치 학습 등을 통해 학습
필요한 노드에 대해 임베딩 벡터 생성

이때 주목할만한 점은 위에서 볼 수 있듯이 계산 그래프의 구조와 관계없이 GNN의 파라미터 $W_l, B_l$ 이 공유된다는 점이다. 이는 학습에 사용되지 않았던 노드들도 임베딩 벡터를 효과적으로 생성할 수 있는 Inductive Capability가 GNN은 가지고 있다고 할 수 있다.