1. Framework

앞선 수업에선 GNN의 대략적인 개념을 살펴보았다. 이제 좀 더 심화된 GNN 모델들을 살펴볼 예정인데, 이때 간단한 모델에 비해 달라질 수 있는 부분이 어디인지 생각해보자.

1. Message
   GNN은 결국 그래프 구조를 따라서 중심이 되는 노드에 메세지를 전달하는 모델이다. 이때, 단순히 노드 변수를 메세지로 삼을 수도 있지만, 다른 요소를 메세지로 삼을 수 있지 않을까?
2. Aggregation
   한 레이어의 input으로 이웃 노드의 벡터를 단순 평균/합 하여 사용하는 방법은 간단하지만 정교하지 못하다. 다른 방법으로 이웃 노드들의 정보를 취합할 수 있지 않을까?
3. Layer Connectivity
   당연한 이야기지만, GNN도 딥러닝 모델이다. 그렇다면 다른 분야에서 활발히 사용되는 residual connection이나, attention을 사용할 수 있지 않을까?
4. Graph Augmentation
   단순하게 기존의 그래프 구조를 계산 그래프로 사용할 수도 있지만, 이보다 효율적으로 계산 그래프를 수정할 수 있을 것이다.
5. Learning Objective
   모델을 잘 만드는 것은 모델 구조 뿐만 아니라 목적함수 역시 포함하는 이야기다. 단순하게 유사도를 맵핑한다는 개념에서 더 나아가 지도/비지도, 노드/엣지/그래프 단위의 목적함수를 꾸려볼 수 있지 않을까?

2. A GNN Layer

GNN 레이어 하나가 작동하는 것을 살펴보면, 크게 두 단계로 나눌 수 있다.

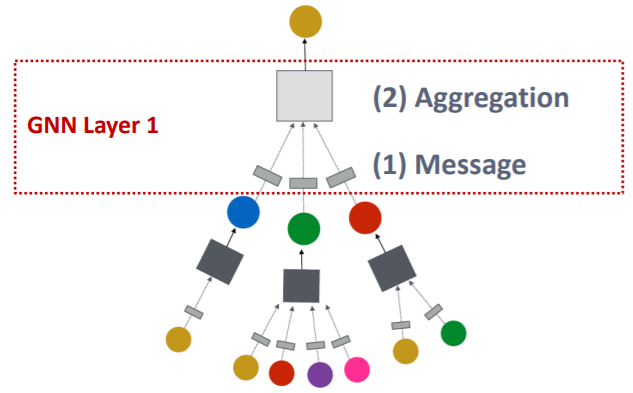
위 그림에서 보이는 것처럼 이웃 노드를 input으로 하여, 1) 각 노드의 벡터를 메세지로 변환하고 2) 변환된 메세지를 종합한다.

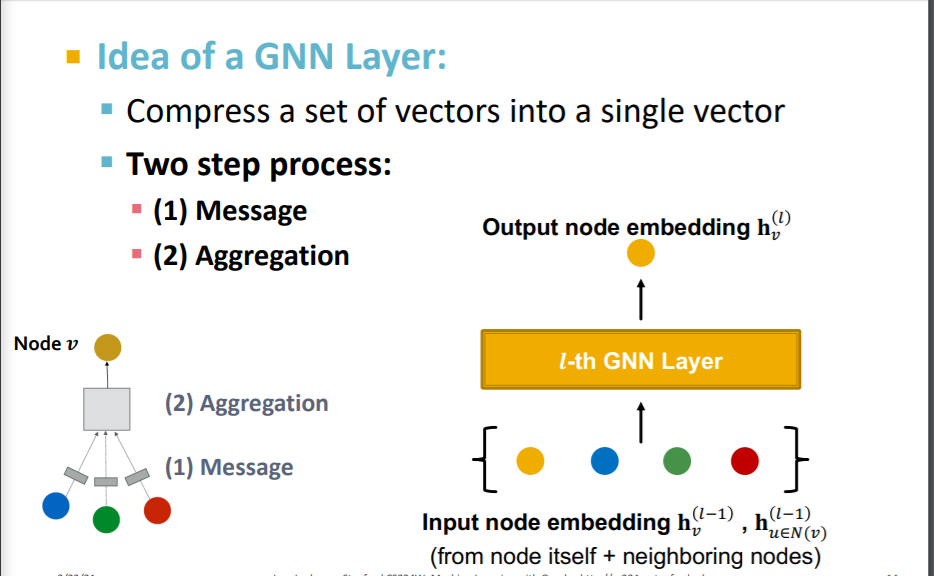
이때 레이어의 인풋은 이웃노드와 현재노드의 직전 레이어에서의 노드 임베딩으로 한다.

Message Computation
메세지를 변환하는 과정을 자세히 살펴보면 다음과 같은 수식으로 구성되어 있다.

이전 레이어에서 온 정보$(h^{(l-1)}_u)$가 이번 레이어의 메세지 변환 함수$(MSG^{(l)})$를 통과하여 이번 레이어의 정보가 된다. 이때, 각 레이어마다 개별적인 메세지 변환함수를 가지고 있다는 점과 각 이웃노드별로 아직은 따로 변환된 메세지를 가지고 있다는 점을 명심하자.

예를 들어 이전 수업에서 선형 변환을 메세지 변환함수로 사용하여 다음과 같이 표시하였다.

Aggregation
각 노드는 변환된 메세지를 가지고 있는데, 이를 종합하는 함수 또한 필요하다. 이때, 그래프는 이웃 노드 간의 우선순위가 없으므로 순서에 영향을 받지 않는(order invariant) 함수를 사용해야 한다. 가장 단순하면서 대표적인 방법으론 합, 평균, 최대값을 사용할 수 있다. 수식으로 표현하면 다음과 같을 것이다.

Nonlinearity
합쳐진 정보는 ReLU나 Sigmoid 등의 비선형 함수를 통해 최종적으로 레이어를 통과하게 된다. 딥러닝에서 비선형 함수를 활성함수로 사용하는 것은 필수적인데, 이를 통해 표현성(expressiveness)를 확보할 수 있기 때문이다. 비선형 함수가 없다면, 단순한 선형 변환의 곱이 중첩된 형태이고, 이는 하나의 선형변환으로 표현될 수 있다.

2-1. Issue

하지만 위의 세 과정 중에 message aggregation 단계에서 살짝 문제가 있을 수 있다. 현재 제시된 식으로 전개될 경우, 노드 v에 대해 정보를 처리하고자 이웃 노드의 정보를 가져오는 것인데, 중심 노드가 무엇인지 분간할 수 없고, 결국 순전파 과정에서 중심노드의 정보를 잃어버릴 여지가 있다. 이에 대한 해결책은 두 가지가 있다.

Message
메세지를 변환하는 과정에서 중심노드와 주변노드에 대해 다른 변환을 가하는 방법이다. 예를 들어 v가 중심노드이고, $u \in N(v)$일 때, 다음과 같이 할 수 있다.

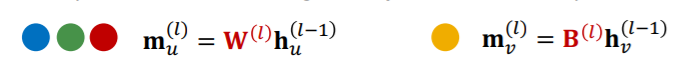
이를 토해 중심노드의 정보가 좀 더 살아서 순전파되도록 만든다.

Aggregation
정보를 종합하는 과정에서도 중심노드의 정보는 주변노드와 다르게 취급되어야 한다. 주변노드와 동일한 연산이 가해지면, 결국 중심노드의 정보가 녹아 사라질 수 있다. 이때, concatenation을 통해 명시적으로 중심노드의 정보를 빼낼 수 있다. 수식으로 표현하면 다음과 같다.

이때 AGG 함수를 통과하는 정보는 이웃노드의 정보가 되고, 중심노드의 정보는 명시적으로 concatenation되어 생생하게 살아 다음 레이어로 전달된다.

2-2. GCN(Graph Convolutional Network)

GCN에서 해당 개념들을 사용하여 구성한 식은 다음과 같다.

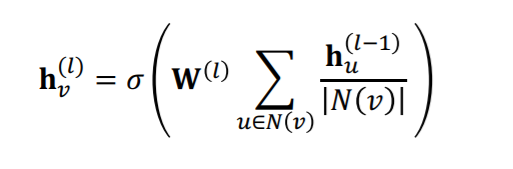
위의 식에서 message transformation과 aggregation이 구분되어 보이지 않는데, 식을 조금 바꾸면 바로 보인다.

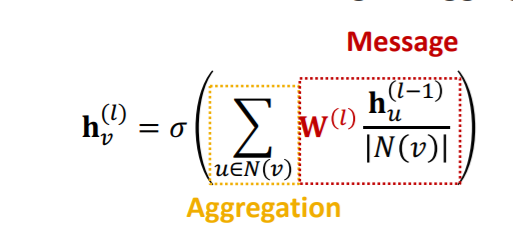
이때 Message Transformation 부분은 각 노드의 정보에 대해 중심노드의 degree로 normalization 해준 후 선형변환하여 처리한다. 이후, 이렇게 처리된 각 이웃노드의 정보를 합하여 aggregation을 한다.

2-3. GraphSAGE

GraphSAGE는 식을 좀 변형하였다. 우선 식부터 보면 다음과 같다.

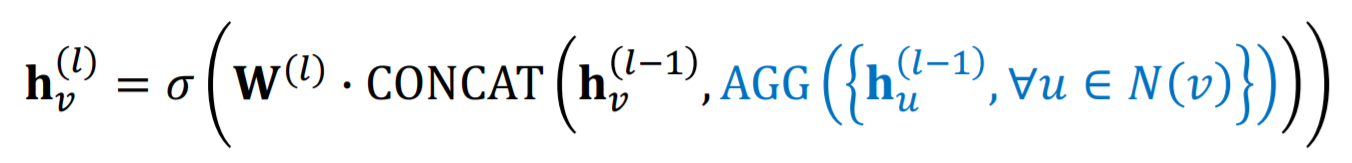
이때 Aggregation이 두 단계를 통해 이루어진다. GCN과 달리 중심노드와 주변노드가 다르게 처리된다는 점을 기억하자.

1. 이웃노드의 정보 합치기
   
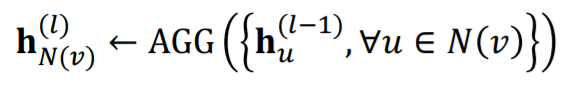
   이웃노드의 정보만 Aggregation 함수를 통해 합친다.
2. 중심노드와 1의 정보 합치기
   
   1을 통해 처리된 정보를 중심노드의 벡터와 concat하여 변환하게 된다.

Aggregation
1의 aggregation 함수는 다양한 함수를 사용할 수 있는데, 대표적으로 세가지가 있다.

1. Mean
   
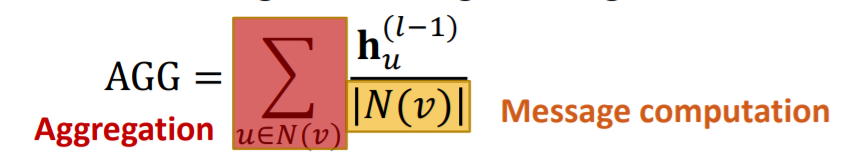
   단순 평균을 이용한 aggregation이다. 이때, message computation은 normalization이 담당하게 된다. aggregation 자체는 단순 합을 이용한다.

2. Pool
   
   message computation은 mlp 등의 함수를 토해 처리하고, aggregation으로 평균이나 최대값과 같은 symmetric vector functino을 이용한다.

3. LSTM
   
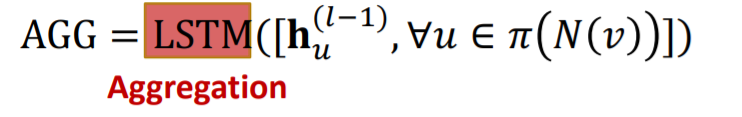
   특이하게 LSTM을 aggregation function으로 이용할 수도 있다. 이때 주의할 점은 LSTM은 sequential model이기 때문에 순서를 학습하게 된다. 하지만 이웃노드의 순서가 가지는 정보는 사실상 없으므로 훈련과정에서 희석하기 위해 계속해서 이웃노드의 순서를 섞어서 학습해야 한다.

$l_2$ Normalization
GraphSAGE 모델은 각 레이어의 output에 대한 l2 norm을 취해준다. 이를 통해 각 레이어를 통과한 output의 norm이 1로 동일해지는 효과를 가지게 된다. 이는 너무 값이 커지거나, 작아지는 것을 방지하고 최종적으로는 성능을 향상시킬 수도 있다고 한다.

3. Graph Attention neTworks(GAT)

그래프에 어텐션 메커니즘을 적용할 수도 있다. 이때의 식부터 살펴보면 다음과 같다.

위의 식에서 기존과 달라진 부분은 $\alpha_{vu}$이다. 이는 message transformation 이후 aggregation 시 각 이웃노드에 어느 정도의 attention을 줄 지에 대한 attention weight이다.

GCN이나 GRraphSAGE에서도 $\alpha_{uv}$가 없던 것은 아니다. 다만 각 이웃노드에 동일한 attention을 주도록 normalization factor로만 사용했다. 즉, 모든 이웃노드가 중심노드에 대해 동일한 중요도, 혹은 동일하게 유용한 정보를 가지고 있다고 간주한 것이다.

3-1. Attention Mechanism for Graph

하지만 모든 이웃노드가 동일하게 중심노드에 유용하지는 않을 것이다. 어떤 이웃노드는 거의 의미가 없을 수도 있고, 어떤 이웃노드는 매우 중요할 수도 있다. attention mechanism은 이를 학습하여 반영하고자 하는 것이다. 이때 attention weight는 중심-주변 노드 쌍에 따라 결정된다. 즉, 노드 $u$가 주변노드로 사용되어도 중심노드가 무엇이냐에 따라 달라지고, 노드 $v$가 중심노드로 사용되어도 주변노드가 무엇이냐에 따라 달라진다. 또한, 한 레이어에서 attention weight의 합은 항상 1이 되어야 한다.

어떻게 attention mechanism이 굴러가는지 자세히 살펴보도록 하자.

1. $e_{vu}$
   $e_{vu}$는 중심노드 $v$에 대한 주변노드 $u$의 절대 중요도를 의미한다. 즉, 중심노드에 대해 주변노드가 절대적 수치로 어느정도 중요한지 나타낸다. $a$가 attention coefficients $e_{vu}$를 계산하는 함수라 하면, 모든 노드 $v, u$ 쌍에 대해 다음과 같이 메세지를 처리한다.
   $\displaystyle e_{vu} = a(W^{(l)}h^{(l-1)}_u, W^{(l)}h^{(l-1)}_v)$
   즉, message transformation 이후에 $a$ 함수를 통과하여 $e_{vu}$를 얻게 된다.
2. $\alpha_{vu}$
   $\alpha_{vu}$는 중심노드 $v$에 대한 주변노드 $u$의 상대 중요도를 의미한다. 즉, 중심노드에 대해 주변노드가 다른 주변노드에 비해 상대적으로 얼마나 중요한지 나타낸다. 이는 소프트맥스 함수를 이용해 다음과 같이 계산되며, 이를 통해 $\sum_{u \in N(v)} \alpha_{vu} = 1$이 된다.
   
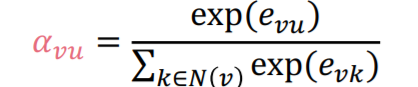
3. embedding vector using attention weight
   attention weight $alpha_{vu}$를 구했기 때문에 이를 이용해 최종적으로 이번 레이어에서의 노드 $v$에 대한 임베딩 벡터를 구할 수 있다. 식으로 표현하면 다음과 같을 것이다.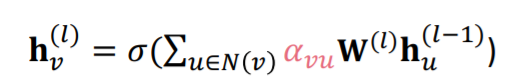

how to get $e_{vu}$
위에서 함수 $a$를 통해 attention coefficients $e_{vu}$를 얻는다고 했다. 그렇다면 함수 $a$는 어떻게 구성되어 있을까? 우선 좋은 함수 $a$가 명확하지 않다고 한다. 다만 흔하게 사용되는 것은 다음과 같다.

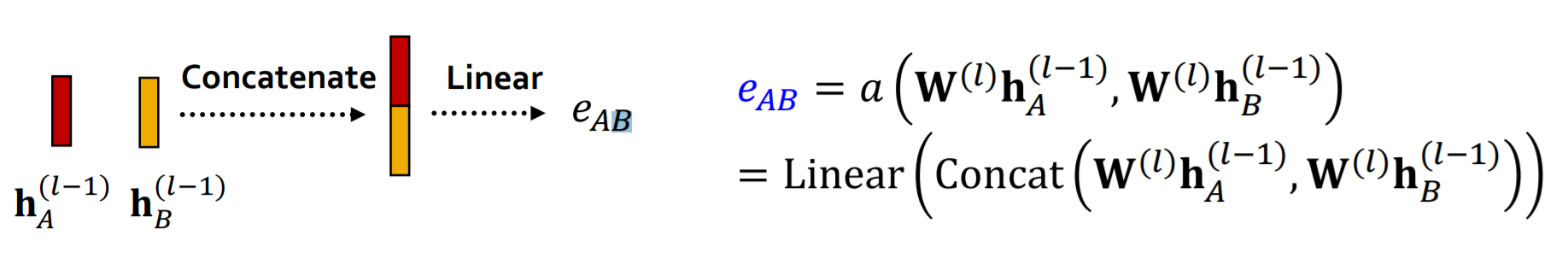
우선 두 노드가 message tranformation된 벡터를 concat하여 입력값으로 한다. 그리고 이를 선형변환하여 $e_{vu}$를 얻게 된다.
위 과정은 조금 무식해보인다. 그냥 선형변환하는데 이웃노드가 유용한 정도를 알아낼 수 있을까? 위 과정이 통하는 이유는 선형변환하는 행렬이 모두 학습되는 파라미터이기 때문이다. 처음에는 제대로 동작하지 않지만, 학습을 통해 점차 동작하게 된다.

Multi-head Attention
트랜스포머처럼 GAT도 멀티 헤드 어텐션을 사용한다. 하지만 그 이유나 방법이 조금 다르다. 위에서 언급했듯이 선형변환 행렬은 학습을 통해 최적화되게 된다. 하지만 실제로 저렇게 선형변환을 통해 attention mechanism을 구현할 경우 잘 수렴하지 못한다고 한다.

이를 개선하고자 다수의 attention score를 사용하여 동일한 단계를 반복하여 진행한다. 즉, 아래 수식과 같이 동일한 방법으로 3개의 임베딩 벡터를 얻게 된다.

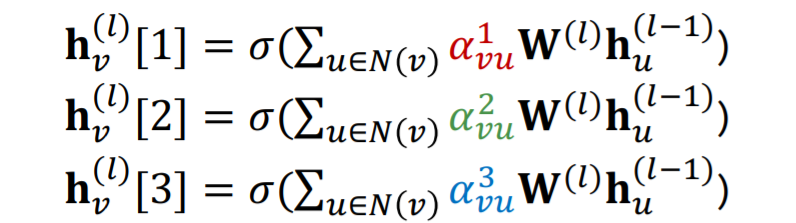
이때 트랜스포머와 다르게 임베딩 벡터를 자르거나, 작은 사이즈의 벡터를 사용하지 않는다. 그럼에도 이것이 의미 있는 이유는 각 선형변환 행렬이 다른 초기값으로 학습을 시작하기 때문에, 다른 local minima에 도달하기 때문이다. 즉, 하나의 행렬이 학습이 불안정하여 쉽게 수렴하지 못하지만, 다수의 point에서 학습을 시작하여 robust하게 학습이 진행되도록 한 것이다.

최종적인 임베딩 벡터는 이를 aggregate하여 얻게 된다.

3-2 Benefits of Attention Mechanism

이렇게 어텐션 메커니즘을 사용하여 얻게 되는 장점은 모두 한 가지에 기인한다.

어텐션 메커니즘은 잠재적으로 중심노드에 대한 각 주변노드의 다른 중요도를 잡아낸다.

1. Computationally efficient
   어텐션 매커니즘은 행렬 연산이 전부이고, 멀티 헤드 어텐션의 경우 병렬처리가 쉽게 진행될 수 있다. 심지어 각 엣지에 대해 병렬적으로 처리될 수 있다. 이는 계산이 매우 빠르고 효율적으로 가능하다는 것을 의미한다.

2. Storage efficient
   그래프를 sparse matrix로 저장할 수 있어 램 관리 측면에서 아주 효율적이다. 또한 고정된 수의 파라미터를 사용하여 그래프의 크기게 영향을 받지 않으므로 또한 램 관리 측면에서 효과적이다.

3. Localized
   어텐션 메커니즘은 이웃노드에만 집중하도록 하므로 전체 그래프 구조를 파악하지 않는다.

4. Inductive capability
   어텐션 메커니즘은 edge-wise 매커니즘이다. 즉, 엣지가 몇 개이든, 그래프의 크기가 어느정도이든 상관없이 적용가능하다.

4. GNN Layer in Practice

당연하게도 GNN에 다른 딥러닝 모듈에서 사용되는 다양한 기법들이 적용가능하다. 이때의 전체적인 레이어 하나의 흐름을 살펴보면 아래와 같다.

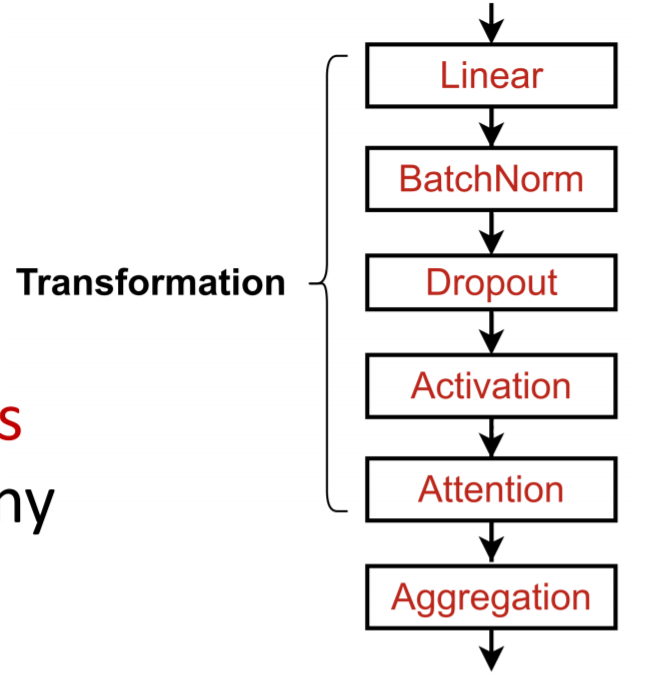
입력으로 이웃노드와 중심노드의 이전 레이어 임베딩이 들어와서 다양한 계층을 통과하고 이번 레이어의 중심노드 임베딩이 생성된다.

이때 주의해야 할 것은 노드 단위로 해당 방법들이 적용되는 것이 아니라, 벡터를 이용해 선형변환 등이 가해질 때 해당 방법들이 적용된다는 점이다. 예를 들어 drop out의 경우 아래와 같다.

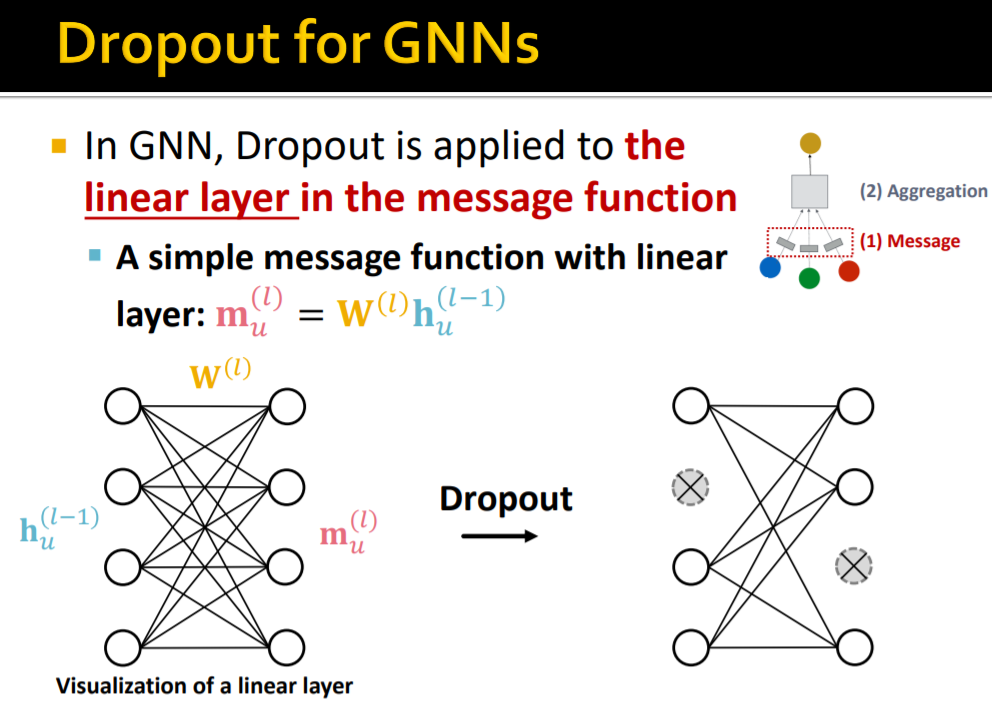
message transformation 시 선형변환이 이루어지는데 이때 drop out이 이루어진다. 노드를 통째로 drop out하지 않는다! 이를 염두에 두면 다른 딥러닝 방법론과 크게 다르지 않다.

5. Stacking GNN Layers

이제 GNN 레이어를 더 깊게 쌓아보도록 하자. 여기서 "깊게"라는 표현은 CNN이나 RNN의 깊게와는 조금 다르다. GNN의 깊게는 직접적으로 그래프에서 중심노드에서 더 많은 hop의 정보를 가져오자는 것이다. GNN 5 layer라면, 5 hop부터 정보를 가져오는 것이다.
하나의 레이어는 다음과 같이 구성되어 있다고 이야기 했다.

1. Message Transformation Operation
2. Message Aggregation Operation

이때, 1과 2 모두 개별적인 모델(DNN, CNN, Attention, LSTM, 선형변환)을 가지고 있다는 점을 명심하자. 하지만 GNN은 CNN처럼 무턱대고 깊게 쌓을 수 없다. Over-Smoothing Problem이 발생하기 때문이다.

5-1. Over Smoothing Problem

Over smoothing problem이란 간단히 말하면 다음과 같다.

모든 노드 임베딩이 비슷한 값으로 수렴하는 현상

우리가 GNN을 통해 노드를 임베딩 시키는 이유는, 노드 분류, 그래프 분류, 엣지 예측, 그래프 예측 등의 태스크를 수행할 때, 그래프, 노드, 엣지 단계에서 각각의 다른 특성들을 파악하기 위해서이다. 만약 모든 노드 임베딩이 비슷한 값으로 수렴한다면, downstream model이 각 노드, 그래프, 엣지를 분간하지 못하게 되고, 결국 원하는 성능이 나오지 않는다.

이에 대한 원인으로는 Receptive Field를 이해하면 알 수 있다.

Receptive Field란 중심노드의 임베딩을 결정할 때 관여하는 노드 집합을 의미한다.

즉, gnn 3 layer라면, 3-hop까지의 이웃노드 집합이 receptive field가 되는 것이다.

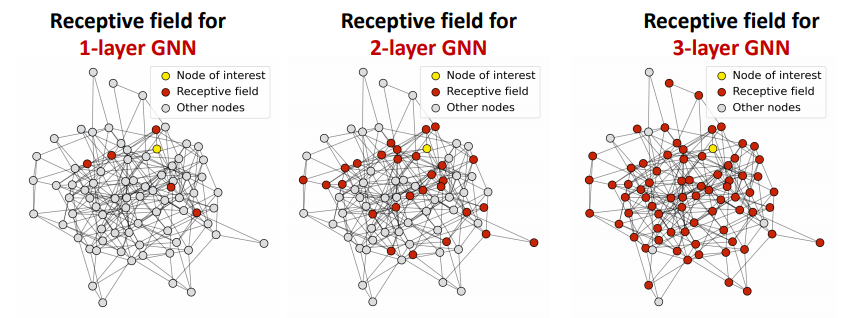
이것이 문제가 되는 이유는 간단하다. hop이 늘어날 수록 receptive field가 급격하게 증가하기 때문이다. 위 그림과 같이 꽤 복잡해 보이는 그래프 구조에서도 3 hop이면 거의 모든 노드가 receptive field에 포함되게 된다.

그런데 중심노드의 임베딩은 receptive field에 의해 결정된다. 위와 같이 항상 거의 모든 노드가 receptive field에 포함되면 거의 모든 중심노드는 비슷한 receptive field를 가지게 되어 비슷한 임베딩이 될 수밖에 없다.

GNN 레이어를 많이 쌓는다 -> 노드들의 receptive field가 매우 비슷해진다 -> 노드 임베딩이 비슷해진다. -> over smoothing problem 발생!

의 논리구조가 완성되는 순간이다.

6. Intuition from Over-Smoothing Problem

6-1. Do not Stack

결국 over-smoothing problem은 gnn은 cnn과 다르게 레이어를 많이 쌓는다고 모델의 성능이 좋아지지 않는다는 것을 의미한다. 그래서 레이어를 적게 쌓으면 문제가 해결된다. 하지만 레이어가 적으면 파라미터의 수가 적고, 모델의 표현력(expressiveness)가 떨어지게 된다. 그래프에서 필요한 정보를 충분히 가져올 수 없는 것이다. 이에 대한 해결방법은 다음과 같이 두가지가 있다.

1. Make Transformation/Aggregation become a Deep Neural Network

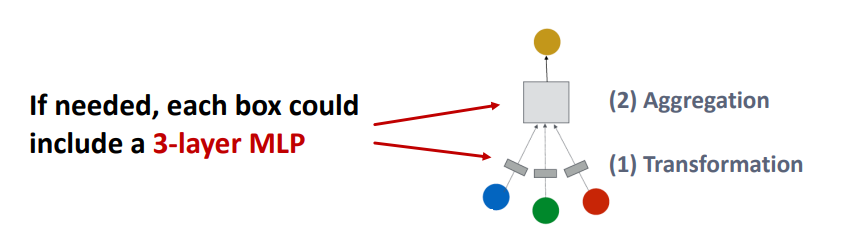
Message Aggregation과 Message Transformation 모두 어떠한 딥러닝 레이어 혹은 affine 변환 레이어를 가지고 있다. 이를 보다 깊게 하면 모델의 표현력은 향상될 수 있다.
2. Add Layers That Do Not Pass Message

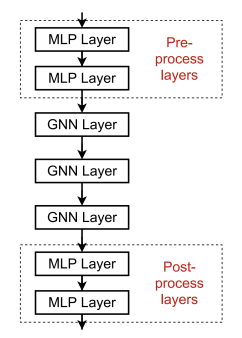
결국 over-smoothing의 문제는 메세지가 너무 많은 receptive field를 지나왔기 때문이다. 그렇다면 메세지를 건들지 않고 모델을 수직적으로 깊게 쌓으면 된다. 위 그림과 같이 각 노드가 이미지나 텍스트를 표현하는 경우 이를 CNN, RNN 등으로 임베딩할 때 더 깊고 복잡한 모델을 사용할 수 있다. 혹은 Down Stream Model을 보다 깊게 하여 임베딩된 벡터가 좀 더 복잡한 함수를 통과하게 만들 수 있다.

6-2. Using Skip Connection

근데 그래도 GNN은 깊게 쌓고 싶다. 여전히 하나의 중심노드는 많은 hop의 주변노드로부터 정보를 받아야할 필요가 있을 것이다. 이때, skip connection을 사용할 수 있다. GNN에서 초기 레이어는 중심노드에서 먼(큰 수의 hop을 가지는) 이웃노드를 의미한다. 레이어가 깊어질수록 더 많은 주변노드의 (이전의 hop의 노드를 포함하기 때문에)정보를 종합하게 된다.
즉, 초기 레이어는 더 적은 수의 이웃노드를 포함하고 있기 때문에 다른 노드간에는 다른 Receptive Field를 의미하게 될 것이다. 이는 초기 레이어의 정보들은 노드를 더 잘 구분하게 해준다는 의미가 된다. 이러한 초기 레이어의 정보가 깊은 레이어까지 잘 전달되도록 skip connection을 이용하는 것이다.

skip connection에 대한 자세한 설명은 트랜스포머나 다른 모델을 설명하면서 많이 했으니 핵심만 다시 이야기해보자. 결국 skip connection은 어떠한 함수 f(x)와 입력값 x를 더하여 해당 레이어의 비선형 함수에 통과시키겠다는 아이디어이다. 수식으로 나타내자면 아래와 같을 것이다.

이는 모델이 해당 레이어를 사용할지 사용하지 않을지 결정하게 해준다. 다른말로, 입력값이 해당 레이어를 거쳐야하는지 통과해야 하는지 결정해준다.

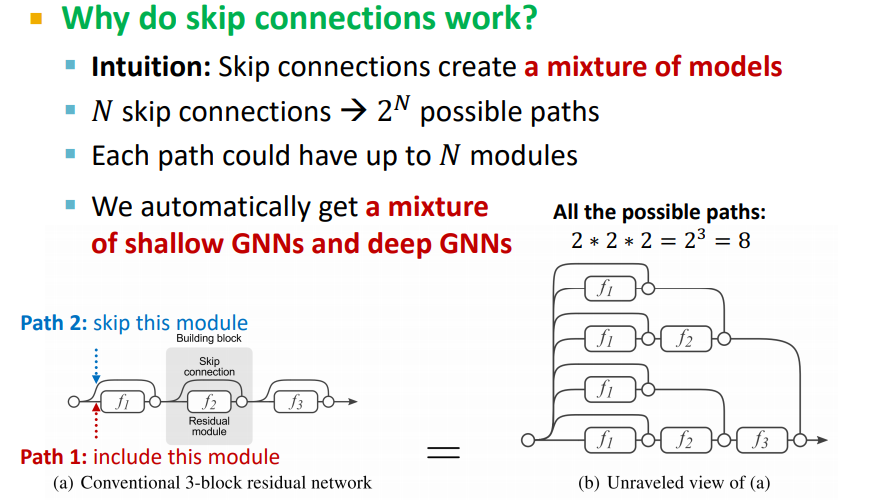
이는 n개의 레이어에 대해 skip connection을 적용하면 입력값이 출력에 이르기까지 총 $2^n$개의 경로의 경우를 가진다는 것을 의미한다. 즉, 어떠한 경우에는 매우 적은 레이어만 통과하여 shallow model처럼 작동할 수도, 어떠한 경우에는 매우 많은 레이어를 통과하여 deep model처럼 작동할 수도 있게 만든다.

GCN에 skip connection을 적용하면 식이 다음과 같이 변하게 된다.

• 본래의 식에서 함수 $F(x)$는 아래와 같은 부분일 것이다.
  
• GCN에서 레이어의 입력값이란 이전 레이어에서의 중심노드의 임베딩 벡터이므로 다음과 같은 항이 추가되면 된다.
  

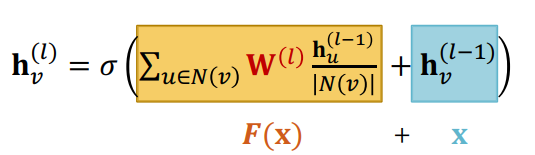
다른 옵션도 있다. 모든 레이어가 자신의 레이어를 skip하게 하는게 아니라, 곧바로 출력으로 skip하도록 설정할 수도 있다. 이를 도식화하면 아래 그림과 같이 된다.

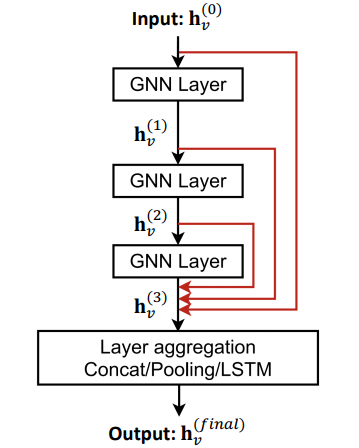
이는 최종 출력은 모든 레이어에서의 임베딩 벡터를 종합(aggregate)하여 최종적인 임베딩 벡터를 만드는 것이다.