[CS224W] Lecture 8 - Applications of Graph Neural Networks

김재희·2021년 8월 26일

CS224W GNN

CS224W

목록 보기

8/11

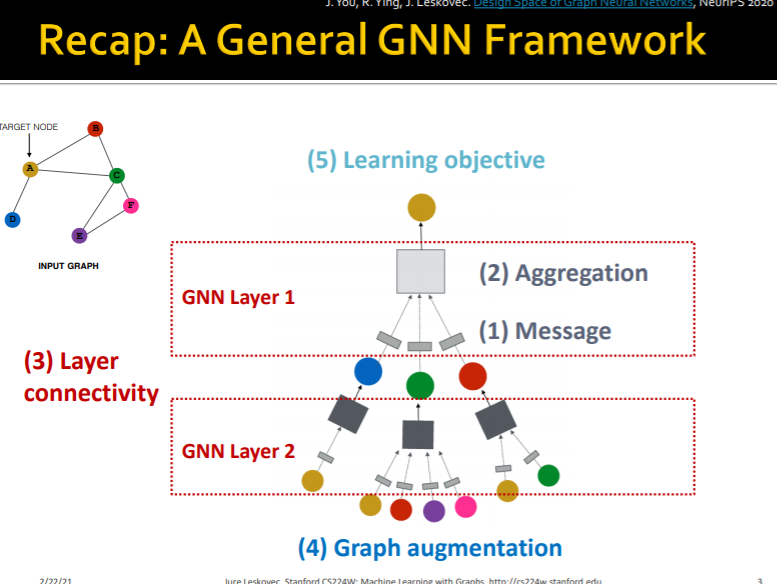
0. Intro

GNN의 Framework는 다음과 같은 요소로 구성되어 있었다.

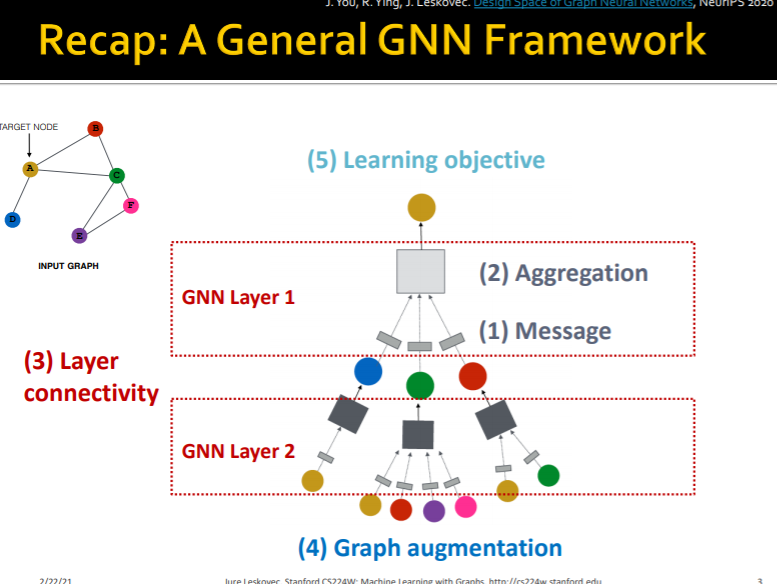
Message Transformation
Message Aggregation
Layer Connectivity
Graph Augmentation
Learning Objective

이전 강의에서 1 ~ 3에 대해 어떻게 더 깊고, 표현력이 좋은 모델을 만들 수 있는지 살펴보았다. 이번 수업에서는 어떻게 그래프를 만져서 계산 그래프를 생성하고, 목적함수를 더 잘 구성할 수 있는지 살펴보도록 하자.

1. Why Augment Graphs

이전까지 GNN에서 계산그래프는 입력으로 들어오는 그래프의 구조를 그대로 사용했다. 즉, 중심노드를 기준으로 n-hop까지의 부분 그래프를 펼쳐서 계산그래프로 사용했다. 하지만 이제는 그래프를 조작하고자 한다. 왜 그래프를 만져야할까?

노드 변수가 부족한 경우가 많다.
이때 전달될 message 자체가 부족하므로 그대로 사용하는 것은 무리가 있다.
-> 변수를 augmentation하여 해결할 수 있다.
그래프가 너무 sparse할 수 있다.
이 역시 message를 모을 이웃 노드가 많지 않다는 문제가 있다.
-> 가상의 노드나 엣지를 추가하여 연결을 더 확보할 수 있다.
그래프가 너무 dense할 수 있다.
이때는 message passing의 과정에서 연산량이 과하게 많아질 수 있다.
-> 전체 이웃노드를 사용하지 않고, 샘플링하여 연산량을 줄일 수 있다.
그래프의 크기가 너무 클 수도 있다.
이는 gpu의 램이 감당하지 못해서 계산 자체가 불가능할 수도 있다.
-> 부분 그래프를 샘플링하여 임베딩을 생성하여 해결가능하다.

위와 같은 여러가지 이유로 그래프의 구조를 조정하여 계산 그래프를 생성하면 학습이 원활히 이루어지고, 임베딩이 효과적으로 생성될 것이다.

1-1. Feature Augmentation

많은 그래프들이 그래프 구조만 가지고, 노드 변수가 없다. 이 경우에 GNN에 직접 적용이 어려운데, GNN은 노드 변수를 직접적인 입력값으로 가지기 때문이다.

Constant Value
이를 해결하는 가장 단순한 방법으론 아래와 같이 모든 노드에 동일한 상수를 배정하는 것이다.

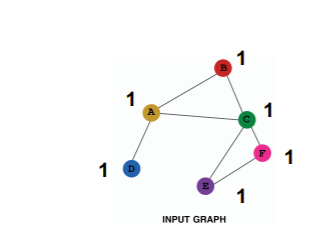
당연히 상수이기 때문에 노드에 대해 가지는 의미는 없지만, GNN의 입력값을 사용할 수 있기 때문에, 노드 임베딩이 가능해진다. 이때는 노드 변수가 가지는 의미가 사라지기 때문에 그래프 구조에서 오는 의미가 클 것이다.

One-hot Vector
모든 노드가 동일한 변수를 가지는게 마음에 들지 않는다면, 좀 더 일반적으로는 one hot vector를 생성할 수 있다.

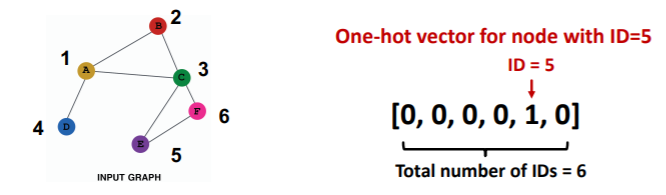
위와 같이 각 노드의 id를 인덱스로 가지는 벡터를 이용하는 것인데, 이를 통해 GNN 명시적으로 각 노드를 구분할 수 있게 된다. 다만 이 방법을 사용할 경우 기존의 그래프에 새로운 노드가 추가될 경우 inference할 방법이 없다는 한계점을 가지고 있다.

두 방법을 비교해보면 아래 표와 같다.

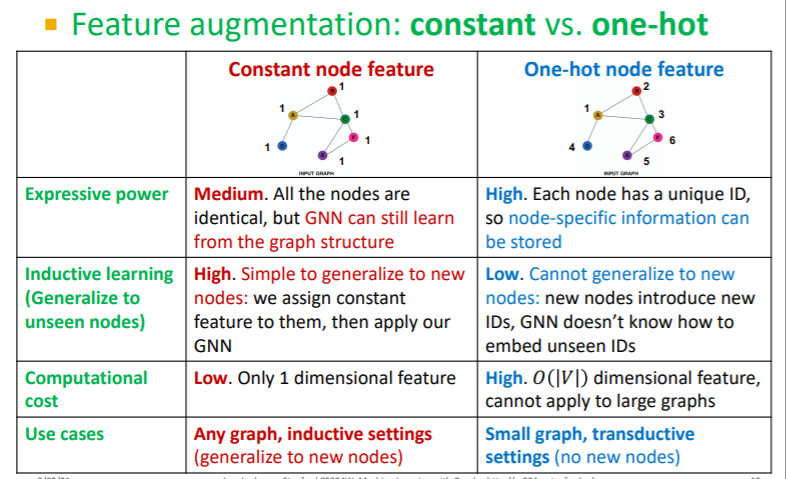
요약해보자면, 상수를 사용하면 1차원 변수를 사용하기 때문에 연산량이 적어 그래프 종류에 관계없이 적용이 가능하고, indeuctive learning이다. 반대로 one hot vector를 사용하면 $\lvert V \rvert$ 크기의 벡터를 변수로 사용하기 때문에 연산량이 많아 작은 그래프에만 적용이 가능하고, inductive learning이 불가능하여 새로운 노드는 임베딩할 수 없다.

단순히 변수가 없을 경우에만 feature augmentation을 진행하지는 않는다. GNN이 특정 그래프 구조에 대해 학습이 잘 이루어지지 않는데, 이를 보완하기 위해서 사용하기도 한다.

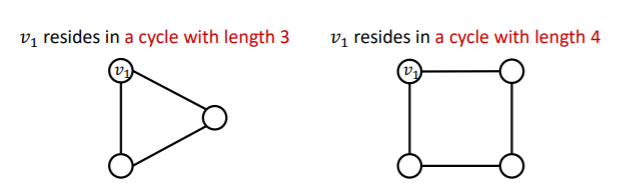
위 두 그래프는 모두 cycle 구조를 가지고 있지만, 분명히 노드의 갯수가 다르다. 하지만 GNN은 두 그래프를 구별하지 못한다.

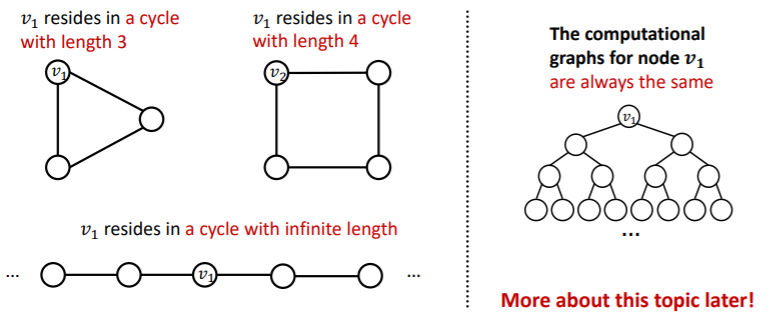
그 이유는 GNN은 이웃 노드를 살피기 때문이다. 즉, 두 그래프 모두 degree가 2인 노드로만 이루어져 있기 때문에, 위 그림과 같이 계산 그래프를 그려보면 binary tree 구조를 가진다.

이를 해결하는 방법은 노드 변수로 그래프 구조를 직접 명시하는 것이다.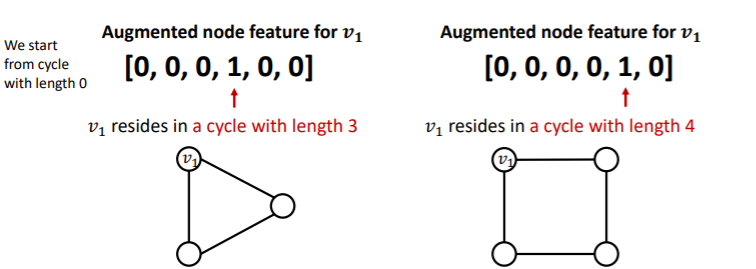

예를 들어 위의 그림처럼 해당 노드가 속한 cycle이 degree 몇짜리 cycle인지 one hot vector로 표현할 수 있다. 이를 통해 GNN은 그래프가 어떤 cycle을 가지고 있는지 파악하고 이를 이용해 임베딩 할 수 있을 것이다.

cycle degree외에도 2강에서 배웠던 수많은 노드 변수들이 직접 GNN의 입력값으로 사용될 수 있다. 변수들이 노드의 정보를 가지고 있다면 훌륭한 변수가 될 수 있개 때문일 것이다.

1-2. Add Virtual Nodes/Edges

두번째 방법은 그래프가 sparse할 경우에 사용할 수 있는 방법이다.

Adding virtual edges
가장 흔한 방법은 2-hop 이웃을 가상의 엣지로 이어주는 것이다. 즉, 원래는 2 hop neighbor인데 이를 1 hop neighbor처럼 간주하도록 하는 것인데 행렬 계산을 통해 간단히 구현할 수 있다. 인접 행렬의 n승은 n-hop neighbor 혹은 n-hop을 통해 갈 수 있는 경로의 수를 나타낸다는 것을 3강에서 배웠다. 이를 이용해서 GNN의 입력으로 인접행렬 $A$ 가 아니라 $A + A^2$ 를 사용하면 가상의 2-hop edge를 추가한 셈이 된다.

이는 bipartite graph에서 효과가 큰데, bipartite graph에서 2-hop이란 각자의 집단에 대한 연결성을 의미하기 때문이다.

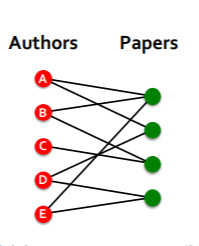
예를 들어 위와 같은 authors-papers graph에서 authors에 대한 2-hop은 공동저자를 의미하고, papers에 대한 2-hop은 동일 저자의 다른 논문을 의미하게 된다. 이를 통해 연결이 부족한 그래프에서 의미있는 엣지를 확보할 수 있게 된다.

Adding virtual nodes
이전에 그래프 임베딩을 다루면서 가상의 노드를 사용하는 것을 배웠었다. 이와 비슷하게 모든 노드와 연결된 가상의 노드를 사용하여 sparse한 그래프에 대한 문제를 해결할 수 있다. 모든 노드와 연결된 가상의 노드를 이용하면 모든 노드가 2-hop으로 연결되게 된다.

만약 서로 거리가 먼 노드가 있다고 할 때, 이 두 노드가 실제론 서로 관련된 message passing 구조를 가질 수 있다. 이를 단순히 가상의 노드를 추가하여 해결할 수 있는 것이다.

1-3. Node Neighborhood Sampling

만약 그래프가 너무 dense한 노드를 가지고 있을 경우 연산량을 줄이기 위해 이웃노드를 전부 사용하지 않고, 샘플링하여 사용할 수도 있다. 예를 들어 트위터 네트워크에서 킴 카사디안이나 레이디 가가 같은 경우 수백만의 팔로워를 가지고 있는데, 이를 전부 이웃노드로 간주하고 GNN을 학습시키면, 해당 계정을 임베딩할때 너무 많은 연산량을 필요로 한다.

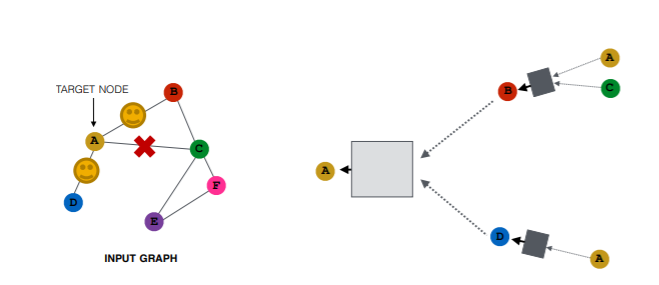
이를 해결하기 위해 위의 그림과 같이 이웃노드를 모두 사용하지 않고, 일부만 랜덤 샘플링하여 계산 그래프를 구성할 수 있다. 이때 매 에포크, 스텝, 레이어마다 샘플링을 고정하지 않고, 다르게 반복하면 아래 그림처럼 동일한 노드 임베딩을 생성하는 계산 그래프가 매번 다르게 생성될 수 있다.

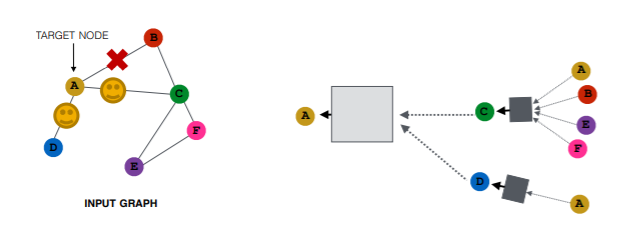
가장 희망적인 경우는 모든 이웃노드를 사용한 경우와 비슷한 임베딩 벡터를 샘플링을 통해서 얻을 수 있을 때이다. 하지만 중요한 정보가 포함된 이웃노드가 샘플링 과정에서 제외될 수도 있기 때문에 나중에 샘플링 방법에 대해 따로 다룬다고 한다.

무엇보다 Neighborhood Sampling을 통해 얻을 수 있는 이점은, 계산량을 줄여, 좀 더 큰 그래프에 GNN을 적용할 수 있거나, 좀더 큰 GNN 모델을 적용하여 모델의 표현력을 높힐 수 있다는 점일 것이다.

2. Prediction head

실제 GNN의 학습은 GNN을 통과하여 생성된 노드 임베딩을 이용해 태스크를 수행하여 손실함수를 계산하여 역전파가 이루어져야 가능하다. 즉, 동일한 GNN 구조더라도 다른 태스크, 다른 손실함수를 사용하면 다르게 학습되게 된다.

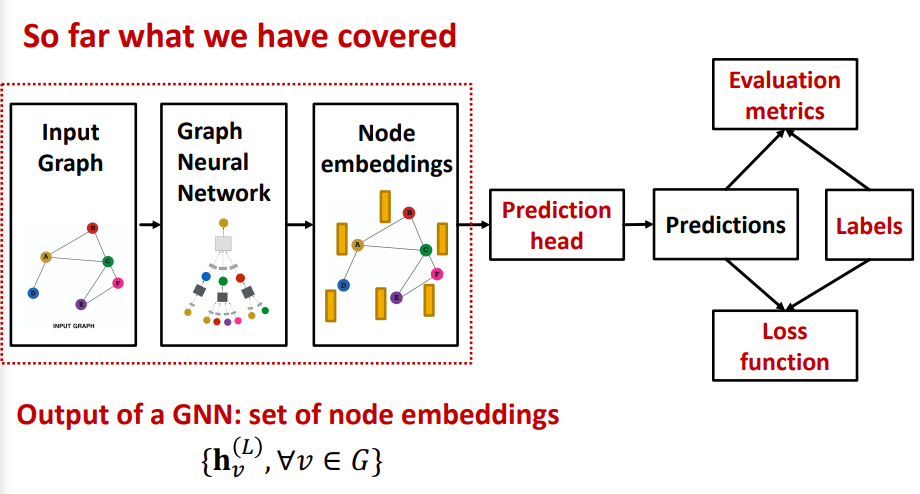
지금까지 다뤄온 GNN의 요소들은 위의 그림에서 왼쪽 부분에 해당한다. 즉, graph augmentation, gnn 구조 등은 예측을 위해 임베딩 벡터를 생성하는 과정에 해당한다.

이번에 다룰 내용은 prediction head로 생성된 노드 임베딩 벡터를 활용하여 어떤 태스크를 어떻게 수행할 수 있는지 살펴보자.

우선 크게 살펴보면 아래와 같은 태스크로 나눌 수 있다.

Node-level tasks
Edge-level tasks
Graph-level tasks

이는 이전에도 전통적인 머신러닝 기법을 다루면서 나누었던 분류와 동일하다. 하나씩 살펴보자.

2-1. Node-level tasks

우리가 GNN을 통해 얻은 노드 임베딩은 다음과 같이 표현할 수 있을 것이다.

\displaystyle \{h_v^{(L)} \in \mathbb{R}^d, \forall v \in G\}

이때 우리가 할 수 있는 태스크는 분류와 회귀로 나눌 수 있고, 이는 다음과 같은 식으로 표현될 것이다.

\displaystyle \hat{y}_v = Head_{node}(h^{(L)}_v) = W^{(H)}h_v^{(L)}

이때 L은 GNN의 레이어 번호를 의미하는 것으로 이 식에서는 마지막 레이어의 출력을 활용하는 것을 알 수 있다. 결국 위의 도식에서 봤던 prediction head 역시 일종의 레이어로 구성되어 있는 것을 알 수 있다. 이때 노드 레벨 태스크는 노드 하나에 대한 예측을 하기 때문에 한 노드의 임베딩 벡터만 입력값으로 받는 것을 알 수 있다. 단순화를 위해 선형변환으로 표현했지만 비선형함수를 활성화함수로 추가할 수도 있을 것이다.

2-2. Edge-level tasks

엣지레벨 태스크를 노드 임베딩을 이용해 수행하기 위해서는 다음과 같이 헤드를 구성해야 한다.

\displaystyle \hat{y}_{uv} = Head_{edge}(h_v^{(L)},h_u^{(L)})

즉, 노드 레벨 태스크와 달리 두 노드 간의 엣지에 대해 예측하기 위해서는 두 노드의 임베딩 벡터를 입력값으로 하는 헤드를 구성해야 한다. 이때 선택지는 다음과 같은 것들이 있을 수 있다.

Concat + Linear

\displaystyle \hat{y}_{uv} = Linear(Concat(h_v^{(L)}, h_v^{(L)})

가장 단순한 방법으론 두 임베딩 벡터를 concat하고 선형변환을 가하는 것이다. 이는 $2*d$ 차원의 벡터를 k(분류 레이블의 갯수) 차원 벡터 혹은 스칼라(이진분류, 회귀)로 맵핑하는 선형함수를 구성하는 꼴이다.

Dot Product
하지만 위의 방법은 문제가 있다. 만약 undirected graph라면 두 노드의 입력 순서는 예측에 영향을 끼쳐서는 안된다. 하지만 위와 같이 concat하고 선형변환을 하게 되면 두 노드의 순서에 따라 다른 값이 나올 수 밖에 없다.

이에 대한 대안이 두 임베딩 베거를 내적하는 것이다. 두 노드의 연결 여부를 예측하는 경우 다음과 같은 단순 내적으로 가능하다.

\displaystyle \hat{y}_{uv} = (h_v^{(L)})^Th_v^{(L)}

만약 다중 레이블에 대한 분류일 경우 선형변환을 추가하여 다음과 같이 구성할 수 있다.

\displaystyle \hat{y}^{(1)}_{uv} = (h_v^{(L)})^TW^{(1)}h_v^{(L)}\\ \hat{y}^{(2)}_{uv} = (h_v^{(L)})^TW^{(2)}h_v^{(L)}\\ \hat{y}^{(k)}_{uv} = (h_v^{(L)})^TW^{(k)}h_v^{(L)}\\ \\ \hat{y}_{uv} = Concat(\hat{y}^{(1)}_{uv}, \dots ,\hat{y}^{(k)}_{uv}) \in \mathbb{R}^k

2-3. Graph-level tasks

그래프 레벨 태스크는 결국 그래프의 모든 노드를 이용해 예측을 해야한다. 이는 이전에도 다룬 것처럼 전체 노드를 일정한 방법으로 변환하여 사용하게 된다.

\displaystyle \hat{y}_G = Head_{graph}(\{h_v^{(L)} \in \mathbb{R}^d, \forall v\in G\})

이때 사용하는 헤드는 결국 그래프 내 노드들의 정보를 종합한다는 점에서 GNN 레이어의 aggregation에 사용하는 것과 비슷한 역할을 하게 된다. 가장 대표적인 방법들은 다음과 같다.

Global Mean Pooling

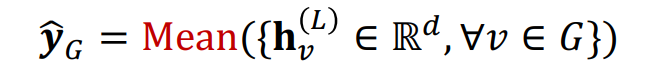
그래프 내 모든 노드의 벡터를 element-wise하게 평균내는 방법이다. 만약 그래프 태스크에서 사용되는 그래프들의 크기가 상이하고, 그 크기에 따른 차이를 무시하고 싶다면 평균을 내어 사용하면 효과적일 것이다.

Global Max Pooling

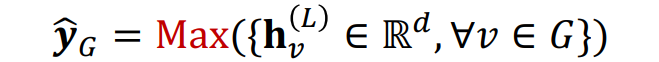
그래프 내 모든 노드의 벡터를 element-wise 하게 최대값을 취하는 방법이다.

Global Sum Pooling

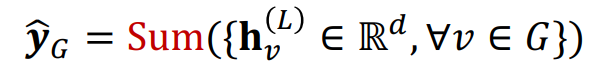
그래프 내 모든 노드의 벡터를 element-wise하게 더하는 방법이다. 평균과 반대로 그래프의 크기가 태스크에서 고려하고 싶다면 이 방법이 효과적일 것이다.

2-4. Global Pooling Problems

위 세가지 방법 모두 작은 그래프에 대해서는 성능이 잘 나오지만 큰 그래프에 대해서는 그렇지 못하다고 한다. 이는 글로벌 풀링이 가지는 근본적인 문제점이라고 할 수 있다.

만약 아래와 같이 1차원 스칼라로 이루어진 노드 임베딩을 가지는 그래프가 두개 있다고 해보자.
$G_1 : \{-1, -2, 0, 1, 2\}$
$G_2 : \{-10, -20, 0, 10, 20\}$

두 그래프의 임베딩을 보면 매우 다르다는 것을 알 수 있다. 하지만 두 그래프에 대해 global sum pooling을 해보면 아래와 같다.
$G_1 : 0 \;\;\; G_2 : 0$
즉 global하게 작동하기 때문에 정보가 뭉개지면서 두 그래프를 구별할 수 없게 되버린다. 이는 global해서 노드의 수가 많아질수록 각 노드의 특징이 전체 그래프 임베딩에서 차지하는 비중이 적어지는 것에 기인한다고 할 수 있다. 노드가 적으면 각 노드가 그래프 임베딩에서 충분히 표현되겠지만, 노드가 많아지면 한 노드의 정보가 그래프 임베딩에 조금만 포함되어 있기 때문이다.

Hierarchical Pooling
이에 해단 해결책은 계층적으로 풀링하는 것이다.

이는 위 그림과 같이 전체 노드를 한번에 풀링하지 않고, 일부 노드를 모아 풀링하여 해당 노드들에 대한 임베딩 벡터를 생성하고, 이 벡터들을 다시 풀링하는 방법을 취한다. 이때 ReLU와 같은 비선형 함수를 추가하여 global pooling과 다른 결과를 가질 수 있도록 한다.

이때 풀링한 일부 노드를 선택하는 것은 일종의 community, sub-graph에 대해 임베딩하는 것이라고 할 수 있다. 즉, 단순히 랜덤한 노드에 대해 풀링하기 보단 지역적으로 모여져 있는 노드들을 하나의 sub graph로 간주하고 이를 단계적으로 pooling하는 것이 효과적이다.

DiffPool
이때 sub graph를 어떻게 구성할 수 있을지에 대한 고민으로 나온 것이 DiffPool이다. 물론 수동으로 구성할 수도 있겠지만, 전혀 현명한 방법은 되지 못할 것이다. DiffPool은 두가지 GNN을 활용하여 매 pooling level마다 독립적인 두 작업을 진행한다.

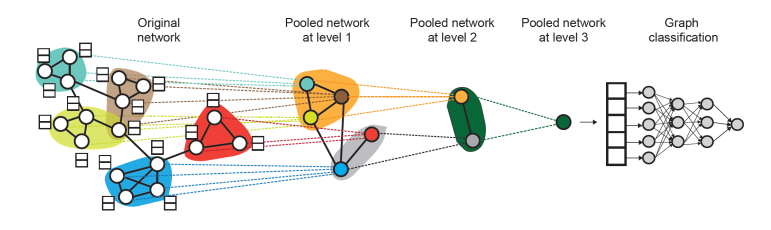
GNN A : 우리가 기존에 활용하는 GNN이다. 즉, 노드, subgraph에 대한 임베딩 벡터를 생성한다.
GNN B : 어떤 노드를 클러스터해야 할지 계산하는 GNN이다.

GNN A, B는 병렬적으로 매 레벨마다 진행되어 효과적으로 임베딩하고, 클러스터링할 방법을 찾게 된다.

3. Prediction & Labels

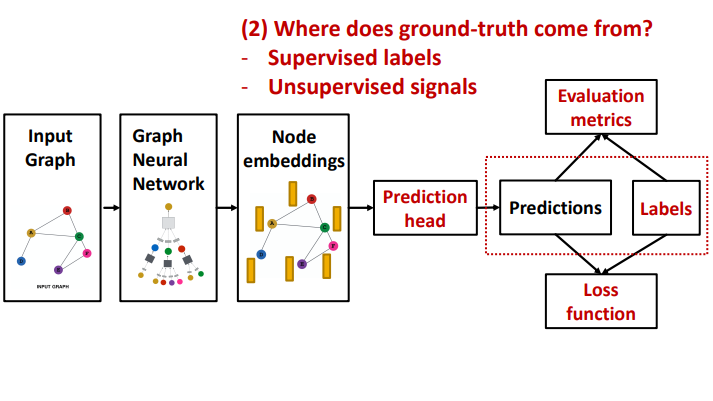
이번에 살펴볼 것은 prediction head를 통과한 예측값과 레이블이다. 즉, 학습의 직접적인 부분을 살펴볼 것인데, 학습은 크게 두가지로 구분된다. 그래프에서 분류를 살펴보면 다음과 같다.

지도학습 : 외부에 출처를 두고 있는 레이블을 가지고 있는 경우
ex) 분자구조에 대한 약효 레이블
비지도학습 : 그래프 스스로 레이블을 가지고 있는 경우
ex) 두 노드의 엣지 존재 유무

즉, 더이상 지도학습과 비지도학습의 구분은 레이블 존재에 있지 않다. Bert 등에서도 볼 수 있는 특징인데 비지도 학습이라 하더라도 데이터 내에서 레이블로 삼을 수 있는 요소를 이용해 일종의 sel supervised learning을 수행하게 된다. 이로 인해 지도학습과 비지도학습의 경계가 모호해지고 있고, unsupervised라는 용어 대신에 self supervised라는 용어로 대체하기도 한다고 한다.

3-1. Supervised Labels on Graphs

그래프에서 지도학습 레이블로는 다음과 같은 것이 있다.

Node labels : 논문 인용 네트워크에서 해당 논문이 가지고 있는 연구분야
Edge labels : 거래 내역 네트워크에서 가짜 거래 여부
Graph labels : 분자구조 네트워크에서 해당 네트워크의 약효

일반적으로 지도학습이 설계하거나 학습시키기 훨씬 수월하고 다양한 방법론들이 개발되었기 때문에, 특별한 사정이 있지 않는한 레이블이 존재한다면 지도학습을 추천한다고 한다.

3-2. Unsupervised Signals on Graphs

비지도 학습에서 가장 큰 문제점은 그래프만 가지고 있고, 이에 대한 레이블이 없어서 학습의 방법이 정해져있지 않다는 점이다. 이에 대해 self supervised learning은 새로운 대책이 될 수 있다. 이 방법은 그래프가 가지고 있는 요소들에서 지도학습으로 사용할만한 요소를 찾는 것이다. 실제 예시로는 다음과 같은 것들이 있을 수 있다.

Node level : 노드 정보, clustering coefficient, pagerank
Edge level : 엣지 유무
Graph level : 그래프 정보. 두 그래프가 위상적으로 동일한지 여부

4. Loss function

손실함수에 대해서는 특별한 내용이 있지는 않았다. 분류와 회귀로 크게 나눌 수 있다.

Classification Loss
이때 분류의 경우 prediction head를 통과한 벡터에 대해 softmax를 취해주어 확률분포의 형태로 만들어주게 된다.

Regression Loss
k 개의 레이블을 가지는 경우에도 MSE를 사용하는 회귀 손실함수가 가능한데, 이는 전체 노드에 대해 실제값보다는 노드의 크기 순서가 중요할 때 사용된다고 한다.

5. Evaluation Metrics

5-1. Regression

회귀에서 흔히 사용하는 지표인 RMSE와 MAE를 간단히 소개했다.

5-2. Classification

Multi-class Classification
다중분류문제에선 단순하게 accuracy만 소개하고 있다.

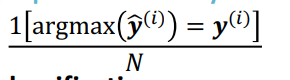
Binary Classification
이진 분류에선 accuracy 외에도 precision, recall, f1-score ROC, AUC에 대해 소개하고 있다.

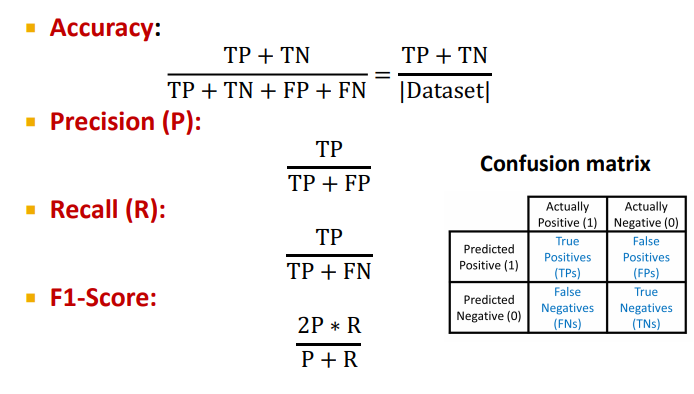
6. Data-Splitting

모델 학습 및 평가를 위해선 Train, Validation, Test 데이터 분리는 필수적이다. 그래프 분야에서도 당연히 데이터를 분리하여 이 절차가 진행되는데 그래프를 다루다 보니 그 과정이 조금 다르다. 우선 데이터를 나누는 방식에 대해 잠시 살펴보자.

Fixed Split
우리가 흔히 알고 있는 분리 방법이다. 하나의 데이터셋을 train, validation, test로 분리시키고 이를 고정하여 사용한다. 이때 각 데이터 추출이 되도록 모집단과 유사하도록 추출하고자 층화추출 등이 사용되지만, 그럼에도 불구하고 각 데이터셋이 편향될 우려는 여전히 존재하게 된다.

Random Split
각 데이터셋이 편향될 우려가 있다면, K-Fold와 같이 여러 번 랜덤하게 데이터를 추출하면 된다. 즉, 동일한 데이터셋에서 시드를 바꿔가면서 세 데이터셋을 추출하고, 각 시드에 대한 모델 성능을 평균내어 최종성능으로 사용할 수 있게 된다.

6-1. Special point of Splitting Graph

그래프는 이미지나 텍스트와 다른 점이 있다. 이미지나 텍스트는 각 데이터가 독립적으로 존재하기 때문에 단순히 랜덤추출하기만 해도 i.i.d. 조건이 어느정도 만족된다고 볼 수 있다.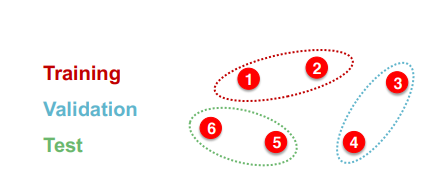
그래서 이미지나 데이터 등의 데이터는 위와 같이 각 데이터가 독립적인 요소로 볼 수 있다.

하지만 그래프는 애초에 각 요소들이 연결되어 있는 구조를 띄고 있다.

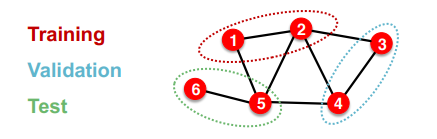
위 그림처럼 train, validation, test라고 임의로 데이터를 추출하여도, 각 데이터셋끼리 상호종속적인 모습을 가질 수 밖에 없다. 이 점에서 기존의 데이터 분리와 다른 점이 등장하게 된다.

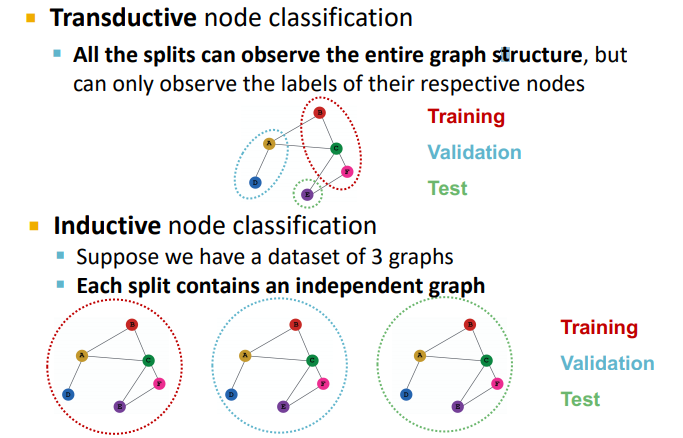
Trasnductive Setting
이 상황에선 하나의 그래프에서 단순히 노드를 추출하는 방법을 사용한다.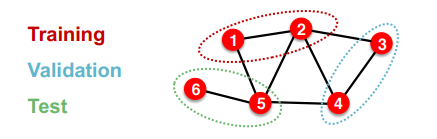
즉, 위 그림과 같이 서로 연결된 노드끼리 다른 데이터셋을 구성하게 된다.

학습 시에는 모든 그래프에 대해 임베딩을 생성하되, 실제 예측 및 손실함수 계산 등 역전파를 위해서는 train에 해당하는 노드만 사용된다. validation 및 test 시에는 동일하게 모든 그래프에 대해 임베딩을 생성하고, validation과 test에 해당하는 노드에 대해서만 성능을 보게 된다.

비록 각 데이터셋이 완전히 독립적이지 않지만, 애초에 그래프 구조는 각 노드가 다른 노드로부터 정보를 받아 GNN을 통과해야 온전한 학습 및 추론 상황이라고 할 수 있기 때문에, 이런 방법을 사용하는 것으로 보인다. 위와 같은 모델링은 결국 그래프 단위의 태스크에는 적용할 수가 없게 된다. 이를 위해선 그래프 단위로 임베딩 벡터가 계산되어야 하는데, 전체 그래프의 일부 노드만 사용하여 학습 및 평가가 진해오디기 때문이다.

Inductive Setting
이 상황에서는 데이터셋 간의 독립성을 강조한다.

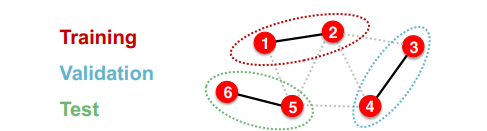
그래서 위와 같이 동일한 그래프에서 노드를 추출하더라도 각 데이터셋끼리의 엣지는 지우고 학습 및 평가에 임하게 된다. 이는 완벽하게 데이터셋을 분리시키고 독립성을 높일 수 있지만, 실제 그래프 구조를 변형시키므로, 학습과 추론이 실제 GNN 모델의 성능과 동일하지 않을 수 있다는 문제점이 존재하게 된다.
하지만 만약 여러 그래프를 가지고 학습이 진행되는 상황이라면 위와 같은 데이터 분리가 어려운 일이 아니고, 이로 인해 모델이 실제 성능을 보이지 못할 우려가 줄어들기도 한다.

6-2. Node & Graph Classification

노드와 그래프 분류 시에는 문제가 다소 쉬워진다.

Node Classification

노드 분류의 경우 이전에 이야기한 transductive & inductive setting 그대로 따라 데이터 분리가 이루어지면 된다.

Graph Classification

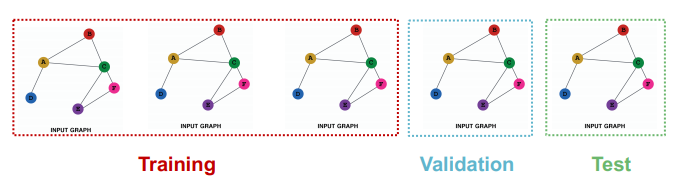
앞서 이야기했듯이 그래프 분류시에는 그래프 임베딩을 생성해야 하기 때문에, inductive setting에서만 데이터 분리가 가능해지게 된다. 이때 각 그래프는 독립적이라고 가정하게 될 것이다.

6-3. Link Prediction

두 노드 간의 엣지 연결 여부에 대한 예측 시에 문제가 까다로워지게 되는데, 레이블이 없기 때문에 Self Supervised Learning을 해야 하기 때문이다. 즉, 이미 존재하는 엣지를 일부 숨기고 이를 맞추는 방식으로 학습과 평가가 진행되어야 한다.

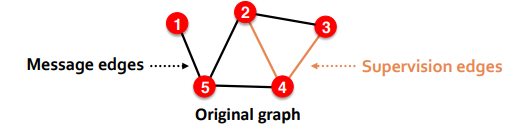
이를 위해 기존에 존재하던 엣지를 두가지로 분리하게 된다. 실제 Message Passing 시 사용하게 되는 Message edges와 message passing에선 사용하지 않고, 예측을 수행하게 될 supervision edge로 나누게 된다.

이젠 데이터셋을 분리해야하는데, 이때 이전과 동일하게 두가지 환경에서 다르게 진행된다.

inductive setting
이때는 단순하다. 그냥 개별적인 그래프를 다른 데이터셋으로 분리하면 된다.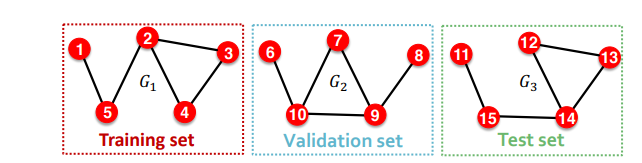
이 경우엔 모든 message edge로 모델을 학습하고, supervision edge로 손실함수 계산 및 역전파 혹은 평가지표 계산을 수행하면 된다.

transductive setting
만약 현재 가지고 있는 그래프가 한가지라면 transductive setting이기 때문에 위와 같은 방법은 사용할 수 없다. 이때는 supervision edge만 각 데이터셋에 따라 분리되게 된다.

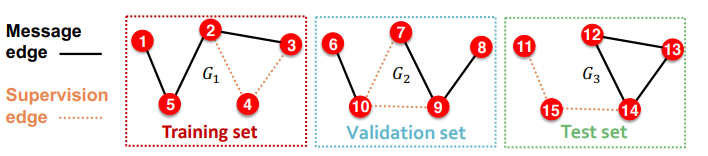
위의 그림을 보면 알 수 있지만, 학습에 사용된 supervision edge는 validation과 test에서 message edge로 전환되어 사용되고, validation에 사용된 supervision edge는 test에서 message edge로 전환되어 사용된다. 왜냐하면 결국 supervision edge도 학습이나 평가에 사용되면서 모델에 정보가 유출된 상황이기 때문에, 굳이 모델 학습 과정에서 제외해야할 이유가 사라졌기 때문이다. 이는 그래프가 시간에 따라 변화하는 모습이라고 간주할 수 있기 때문에, transductive setting은 결국 시간에 따라 데이터셋을 분리한 것이라고 볼수 있게 된다.