0. Vanishing Gradient

0-1. What is Vanishing Gradient

rnn 모델에서 위와 같이 역전파를 시킬 때를 생각해보자. 체인 룰을 이용해 $h_1$에 대한 미분을 계산하면, 다음과 같은 식이 된다.

${\partial J_4 \over \partial h_1} = {\partial J_4 \over \partial h_4}{\partial h_4 \over \partial h_3}{\partial h_3 \over \partial h_2}{\partial h_2 \over \partial h_1}$

여기서 ${\partial h_4 \over \partial h_3}{\partial h_3 \over \partial h_2}{\partial h_2 \over \partial h_1}$ 이 세 값이 매우 작다면, 전체 미분값 역시 무척 작아질 수 밖에 없다.

여기서 rnn이 가지고 있는 vanishing gradients 문제가 드러난다.

rnn의 hidden state의 식은 다음과 같이 이전 시점의 hidden state와 이번 시점의 x, bias로 구성된다!

그리고 위에 나온 식처럼 ${\partial h_t \over \partial h_{t-1}}$을 계산해보면 다음과 같이 $W_h$가 나오게 된다.

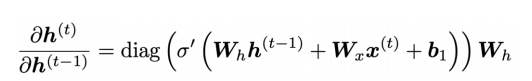
위 식을 이용해 $h_j$에 대한 미분식을 일반화해보면 다음과 같다.

여기서 $W_h$가 시점의 차이만큼 곱해지는 것을 볼 수 있는데, 이 항이 문제가 되는 항이다.

matrix norm의 정리를 통해 다음과 같은 일종의 upper bound를 유도할 수 있다.

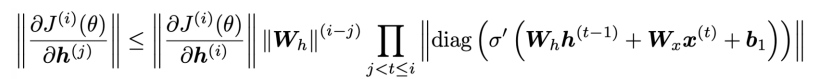
여기서 만약 $W_h$의 아이겐 벨루 중 가장 큰 값이 1보다 작다면, 즉, $W_h$가 선형 변환의 크기가 줄어드는 행렬이라면 결국 ${\partial J_i \over \partial h_t}$는 t와 i가 멀어질 수록 0으로 수렴하게 된다. 반대로, 아이겐 벨류가 1보다 크다면, 발산하게 된다.

그래디언트가 역전파 되면서 점점 그 크기가 작아지는 것을 vanishing gradient라고 한다.

0-2. Why Gradient Vanishing gradient is a problem?

그렇다면 왜 이게 문제일까? 위의 그림을 보자. LM과 같이 many to many 일때, 다른 시점에서 들어온 두 그래디언트가 $h_1$으로 가고 있다. 그런데 $J_4$에서 나온 그래디언트는 시점이 멀어서 $J_2$에서 나온 그래디언트에 비해 절대적으로 작아지게 된다. 즉, rnn 모델이 먼 시점 간의 관계를 제대로 파악할 수 있도록, 파라미터가 업데이트 될 수 없어진 것이다.

위와 같은 문장이 있다고 하자. 여기서 빈칸에 들어갈 단어는 ticket으로 첫 줄에 나온다. 그래디언트가 제일 처음까지 무사히 전달되어야 긴 시점의 정보에 대한 학습이 이루어지게 되는데, 애초에 rnn은 시점이 길어지면 그래디언트가 작아져서 제대로 업데이트가 되지 않으니, 긴 시점의 정보는 전달하지 못하는 모델이 되어 버린 것이다.

0-3. Why Gradient Exploding is a problem?

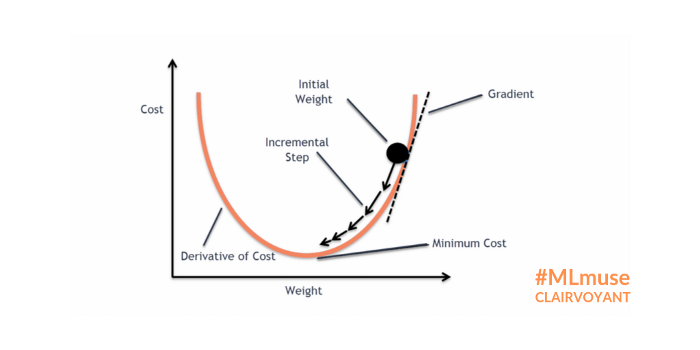
반대로 발산할 경우 역시 문제가 된다. gradient descent에서 그래디언트는 파라미터가 향할 방향에 대한 암시이지, 그 강도에 대한 이야기가 아니다. optimal point는 얼마나 멀리 있는지 알지 못하기 때문이다. 그래서 learning rate을 줄여서 방향성만 잡아주는 것이다. 그런데 그래디언트가 발산하거나 무척 커지게 되면, learning rate도 소용이 없고, 마냥 파라미터가 진동하면서 커지고 결국 Nan이나 Inf와 같은 절망적인 예측값을 보게 되는 것이다.

0-3-1. Gradient Clipping

그래디언트가 폭발하는 것을 막아주는 것이 그래디언트 클리핑이다. 그래디언트 클리핑이란, 그래디언트를 담고 있는 행렬 g의 norm이 너무 크다면, 즉 그래디언트 값들이 threshold보다 커지면, 행렬의 norm을 threshold로 줄인다. 이대, element wise divide이기 때문에 그래디언트들의 크기는 줄어들어도 방향은 바뀌지 않는다. 즉, 업데이트 될 방향은 그대로이고, 그 크기만 바꿔주는 것이다.

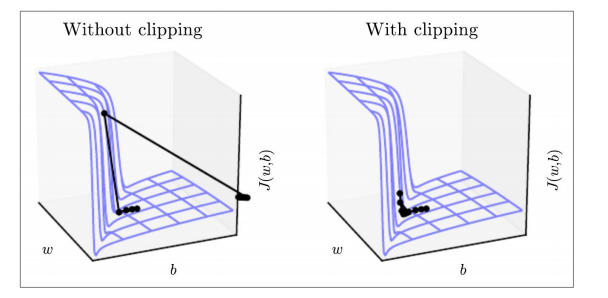
위 그림이 그 모습을 잘 보여주고 있는데, 절벽처럼 보이는 구간이 있다. 해당 구간은 매우 짧기 때문에, 업데이트 할 보폭은 작아도 된다. 하지만, 일반적인 gradient descent 방법을 사용하면 기울기에 비례하여 이동하기 때문에 좌측 사진처럼 엉뚱한 곳으로 shooting해버린다. 그에 비해 클리핑을 이용해 그 보폭의 최대치를 조정해주면, 안정적으로 절벽을 내려오는 모습을 볼 수 있다.

1. Long Short-Term Memory(LSTM)

rnn의 이러한 gradient vanishing problem을 개선하여 개발된 모델이 LSTM이다. rnn은 sequential data를 처리하기 위해 개발된 모델이라고 볼 수 있다. 일반적인 dnn, cnn과 달리 연속적으로 입력값이 존재하고, 각 시점마다 상관관계가 있어서, 이전 시점의 정보가 현재 시점의 정보를 처리할 때 필요한 데이터들 말이다. 그래서 이를 hidden state에 저장하고 이용한다. LSTM의 기본적인 아이디어도 이와 다르지 않다. 다만 이름에서도 볼 수 있듯이 정보를 저장하는 공간을 두 개로 나누어 하나는 장기기억을 다른 하나는 단기기억을 담당하도록 했다. 장기기억을 담당하는 곳을 cell state, 단기기억을 담당하는 곳을 hidden state이라고 하겠다.

1-1. Model Architecture

1-1-1. gate

LSTM은 게이트라고 하는 것을 가지고 있다. 게이트란 정보가 지나갈지 말지 정하는 장치로 쓰인다. 이를 단순히 이분법적으로 나누지 않고, 0 ~ 1사이로 정하여 해당 비율만큼 해당 element의 정보가 지나갈 수 있도록 만들었다.

1-1-2. Equation

LSTM의 식은 다음과 같다.

$f_t = \sigma(W_fh^{t-1} + U_fx^{t}+b_f)$
$i_t = \sigma(W_ih^{t-1} + U_ix^{t}+b_f)$
$o_t = \sigma(W_oh^{t-1} + U_ox^{t}+b_f)$
$\tilde{c_t} = tanh(W_ch^{t-1} + U_cx^{t}+b_f)$

$c_t = f_t *c_{t-1} + i_t*\tilde{c_t}$
$h_t = o_t*tanh(c_t)$

forget gate($f_t$)

$f_t$는 forget gate로 cell state의 이전 정보를 얼마나 잊어버릴지 정한다. 그리고 이를 정하기 위해서 이전 시점의 hidden state와 현재 시점의 입력값을 이용한다. 시그모이드 함수로 싸여 있기 때문에 0 ~ 1의 output을 가지게 된다.

input gate($i_t$)

$i_t$는 input gate로 cell state에 현재 시점의 정보를 얼마나 실을지 결정한다. 그리고 forget gate와 마찬가지로 이전 시점의 hidden state와 현재 시점의 입력값을 이용한다. 시그모이드 함수로 싸여 있기 때문에 0 ~ 1의 output을 가지게 된다.

output gate($o_t$)

$o_t$는 output gate로 현재 시점의 cell state의 어느 정보를 현재 시점의 hidden state로 내보낼지 정하게 된다. 즉, 장기 기억에서 단기기억으로 정보를 옮기는 역할을 하게 되는 것이다. 그리고 forget gate와 마찬가지로 이전 시점의 hidden state와 현재 시점의 입력값을 이용한다. 시그모이드 함수로 싸여 있기 때문에 0 ~ 1의 output을 가지게 된다.

New Cell content($\tilde{c_t}$)

$\tilde{c_t}$는 현재 시점의 정보를 가공한 것으로, 장기 기억에 실을 현재 시점의 정보이다. 그리고 forget gate와 마찬가지로 이전 시점의 hidden state와 현재 시점의 입력값을 이용한다. 즉, 실제로 실을 정보는 new cell content에 담기게 된다.

Cell state($c_t$)

위에서 $*$는 element wise product이다. 쉽게 말해 그냥 element끼리 곱하라는 기호이다. cell state는 forget gate를 통과하여 이전의 정보를 일부 지우고, input gate를 통과한 new cell content가 더해져 현재 시점의 cell state가 완성이 된다.

hidden state($h_t$)

hidden state는 단기 기억이다. 즉, 이전의 $h_{t-1}$을 직접 이용하여 $h_t$를 만들지 않는다. 단기기억은 시간이 지나면 잊혀지기 마련이다. 대신, $h_t$는 현재 시점의 cell state가 output gate를 통과하여 만들어진다. 굳이 $h_{t-1}$을 사용하지 않는 이유는 밑에서 설명된다.

1-1-3. Visualization

그림으로 위에서 언급한 내용을 다시 상기하면 이해가 한결 쉬울 것이다. cell state는 내부 정보로 바깥에서 접근이 불가능하고, hidden state가 각 시점의 최종 output이 된다는 점을 기억하자.

2. Gated Recurrent Units(GRU)

LSTM은 좋은 모델이다. 1990년대 후반 등장해 2010년대에 활발히 사용되었다고 한다. 하지만 모델에 너무 많은 요소가 과도하게 들어있다. 이를 좀더 단순화시켜 모델을 가볍게 만든 것이 GRU이다. GRU는 cell state와 hidden state를 다시 합하여 hidden state 만으로 긴 시점의 정보들이 잘 흐를 수 있도록 만들었다. 다르게 이야기하면, 긴 시점의 역전파가 잘 일어나도록 했다.

2-1. Model Architecure

2-1-1. Equation

$u_t = \sigma(W_uh^{t-1} + U_ux^{t}+b_u)$
$r_t = \sigma(W_rh^{t-1} + U_rx^{t}+b_r)$

$\tilde{h_t} = tanh(W_h(r^t*h^{t-1}) + U_hx^t + b_h)$
$h_t = (1 - u_t)*h^{t-1} + u^t*\tilde{h^t}$

GRU는 두 개의 게이트만 존재한다.

update gate($u_t$)

update gate는 이전의 hidden state에서 얼마나 이번 시점에 만들어진 정보를 집어넣을지를 결정한다. 이는 LSTM의 forget gate와 input gate의 역할을 일부 하고 있는 것이다. LSTM과 마찬가지로 시그모이드 함수를 사용하여 0 ~ 1사이의 값을 가지며, element wise product를 통해 hidden state와 곱해지게 된다.

reset gate($r_t$)

reset gate는 현재 시점의 정보를 만들 때, 얼마나 이전 시점의 정보를 잊어버리고, 현재 시점의 입력값을 사용할 지 정한다. 즉, reset gate 하나가 lstm의 forget gate와 input gate의 역할을 일부 담당하고 있는 것이다.

New hidden state content($\tilde{h_t}$)

$\tilde{h_t}$는 현재 시점의 입력값과 이전 시점의 hidden state를 조합하여 이번 시점에 새로이 hidden state에 집어넣을 정보이다. LSTM과 비교한다면 lstm에서 $\tilde{C_t}$를 만든 것과 비슷하다고 할 수 있다. 다만, reset gate를 이용하여 $\tilde{h_t}$ 내부에서 이전 시점의 정보가 일부 지워진다는 점에서 다르다.

hidden state($h_t$)

hidden state는 이제 $\tilde{h_t}$와 update gate를 통해 업데이트 되게 된다. update gate만큼 새로운 정보가 실리고, 1 - update gate만큼 이전 시점의 hidden state의 정보가 지워지게 된다.

2-1-2. Visualization

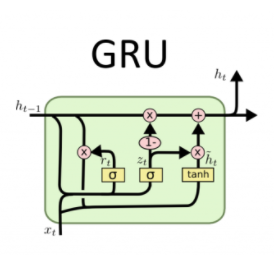
2-2. LSTM vs GRU

그래서 두 모델 중 무엇이 더 낫냐고 물어볼 수 있다. LSTM은 좀 더 무겁고, GRU는 좀 더 가볍다. 하지만 상황에 따라 달라지게 된다. LSTM은 비교적 장시간 의존성을 잘 잡아내는 모델이기 때문에 디폴트 모델로 사용해볼만 하다. 하지만 어떤 태스크에선 GRU가 LSTM 못지 않은 성능을 내면서도 더 빠른 학습 속도를 보인다. 그래서 GRU도 한번쯤 시도해보는 것이 좋다.

3. How can I solve the Vanishing or Exploding Gradient Problem?

사실 vanishing or exploding gradiet problem은 rnn만의 문제는 아니다. dnn이든 cnn이든 네트워크가 깊어지면 자연스레 발생하게 된다. 초기 레이어는 체인룰이나 활성화 함수의 문제로 인해 그래디언트가 잘 전달되지 않고 이로인해 학습이 아주아주 느리게 진행된다. 초기 레이어까지 온 그래디언트는 손실함수와 상관없이 아주 작은 값을 가지게 되기 때문이다. 이를 해결하는 범용적인 방법들(자연어든 이미지든 상관없이)이 몇가지 있다.

3-1. Residual Connection

Resnet에서 처음 소개된 residual connection은 아래 그림과 같은 구조를 가진다.

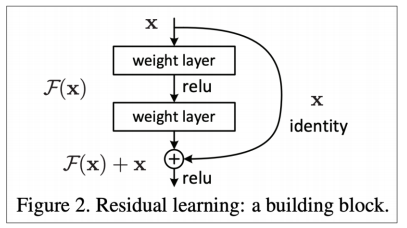
단순하게 하나의 activation function을 통과하고, 선형 변환을 가한 이후에, 이전 선형 변환 직전의 입력값을 그대로 더해주는 것이다. x -> linear transformation(1) -> activation(1) -> linear transformation(2) -> activation(2)일 때, linear transformation(1) -> activation(1) -> linear transformation(2)을 맵핑 함수 F(x)라고 보고, F(x) 대신에 F(x) + x를 출력값으로 하는 것이다.

이렇게하면 얻는 이점은 꽤 강력하다. x가 일종의 고속도로 역할을 하여 그래디언트가 소실되지 않고 잘 전달되도록 한다. 왜냐하면 미분 시 F(x) + x가 덧셈으로 연결되어 있기 때문에 x로 그래디어트가 그대로 흘러가고 x의 미분이 1이기 때문에 그대로 이전 레이어로 그래디언트가 전달될 수 있게 된다.

4. Bidirectional RNNs

rnn류의 모델들은 우리가 언어를 이해하는 방법을 꽤 모사하는 것처럼 보인다. 우리도 글자를 왼쪽에서 오른쪽으로 읽고, 이전의 정보를 기억하며 지금의 정보를 이해하게 된다. 하지만 정말 그럴까?

the movie was terribly exciting!

위와 같은 문장이 있다고 해보자. 여기서 terribly라는 단어는 앞의 정보만 사용하면 끔찍하게와 같이 부정적인 의미로 해석된다. 하지만 뒤의 exciting!이라는 단어를 읽고 나면 완전, 엄청과 같은 뜻으로 바뀌게 된다. 즉, 문장을 이해할 땐, 단순히 왼쪽에서 오른쪽으로 정보가 흐르지 않는다. 종종 오른쪽에서 왼쪽으로 역방향으로 정보가 흐르게 된다.

그리고 RNN류의 모델들은 이를 반영할 필요가 있다. 이에 우리는 이제 RNN을 양방향으로 흘러보낼 것이다.

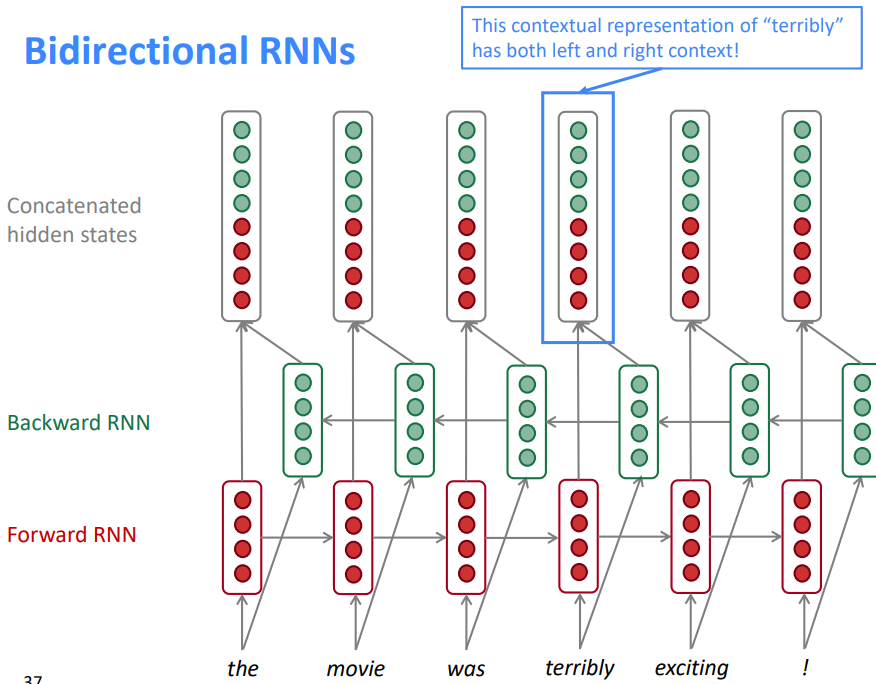
위의 모습이 birectional rnn류 모델 한 층이다. 이전과 달라진 점이라면 녹색의 cell이 생긴것이다. 녹색의 cell은 !부터 시작하여 역순으로 정보가 흘러가게 된다. 그리고 hidden state는 양 방향의 cell을 concat하여 만들어진다. 양방향의 모델링은 개별적으로 이루어지지 않고, 함께 이루어지게 된다.

Cautions

Bidirectional한 모델링을 할 때 주의할 점이 있다. 바로, 실제로 그렇게 정보를 활용할 수 있는지 고려해야 한다. Language Modeling을 다시 생각해보자. 이전에 등장한 단어들을 바탕으로 이후에 등장할 단어를 예측해야 한다. 즉, 현재 시점 이후의 정보는 모델 관점에서 접근할 수 없는 정보들이다. 이때에는 Bidirectional한 모델을 사용할 수 없다. 이 점은 무척 중요하다. 이후에 등자하는 BERT, GPT와 같은 모델들 모두 이 관점을 따르고 있기 때문이다.

5. Stacked RNNs

cnn 기반의 모델들은 수백층 이상을 쌓기도 한다. RNN 기반 모델은 그럴 수 없을까? 제한적으로나마 그럴 수 있다. 그렇게 여러층 쌓인 rnn 모델을 stacked rnn이라고 한다.

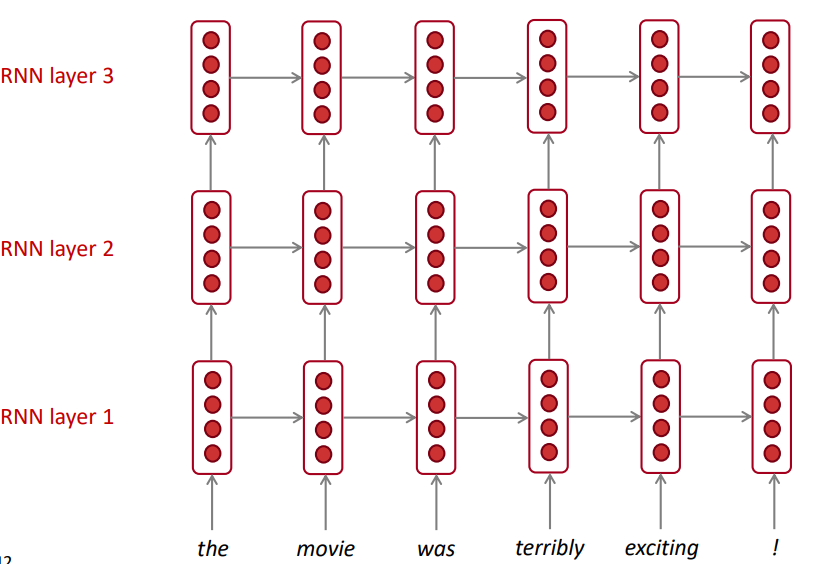
위의 그림은 stacked rnn이다. 3층을 쌓았는데, 이전 층의 hidden state가 다음 층의 input으로 사용되는 것을 볼 수 있다. 마지막 층을 제외하고는 모든 시점에서 hidden state을 뽑아야한다. 이렇게 rnn을 깊게 쌓는 것은 더 복잡한 함수를 형성하게 되고, input들의 더욱 복잡한 관계를 파악할 수 있게 한다.

하지만 rnn의 특징으로 인해 cnn과 달리 수백층씩 쌓을 수 없다. rnn은 sequential modeling이다. 이 말은, 이전 시점의 연산이 종료되어야 다음 시점의 연산이 시작될 수 있다는 것이다. cnn은 채널 간 독립적으로 연산이 이루어지기 때문에 gpu를 활용하여 분산처리가 가능하지만, rnn은 애초에 이전의 연산이 종료될 때까지 기다려야 하므로 시점이 길어지거나 층이 늘어날수록 연산량이 무척 커지게 된다. 이로인해 Google에서도 rnn을 이용한 기계번역에선 2 ~ 4층의 stacked rnn을 사용했다고 한다. skip connection을 추가하여도 8층이 한계였다고 한다.

나중에 배우겠지만 transfomer는 병렬처리를 가능하게 만든 모델이다. 이를 통해 24층까지 레이어를 확장하여 더욱 높은 성능을 보이고 있다.

---

참고

https://www.youtube.com/watch?v=QEw0qEa0E50&t=2679s
https://web.stanford.edu/class/archive/cs/cs224n/cs224n.1194/
https://en.wikipedia.org/wiki/Long_short-term_memory
http://dprogrammer.org/rnn-lstm-gru