0. Intro

이번엔 지금까지 배웠던 다양한 GNN 모델에 대해 한번 다시 생각해보는 시간을 갖도록 하자. GNN의 핵심적인 아이디어는 결국 이웃 노드의 정보를 이용해 노드 임베딩을 생성하는 것이다. 이때 1) 이웃노드의 정보를 모으고 2) 모아진 정보를 가공하여 각 레이어에서의 노드 임베딩을 생성한다. 예를 들어 GCN은 1) element-wise mean pooling으로 이웃 노드의 정보를 모으고, 2) 선형변환 + ReLU를 통해 모아진 정보를 가공한다. GraphSAGE는 1) element-wise max pooling으로 이웃 노드의 정보를 모으고 2) MLP로 모아진 정보를 가공한다. 그렇다면 어떻게 GNN 모델이 그렇게 풍부한 표현력을 가지게 되었고, 어떻게 하면 그 표현력을 극대화한 모델, 즉, GNN 모델이 가질 수 있는 가장 효율적인 구조를 디자인 할 수 있을까?

1. Node Color

GNN은 그래프에 대해 두가지 관점에서 접근하는데, 하나는 각 노드가 가지고 있는 변수들(이미지, 텍스트 등등...)을 이용하고, 다른 하나는 그래프 구조를 이용한다. 이번에는 각 노드의 변수를 색으로 표현해보자. 즉, 동일한 색을 가진 노드는 동일한 변수를 가지고 있다. 그렇다면 GNN이 각 노드의 local neighborhood structure를 이용해 노드를 구분하는 과정을 살펴보도록 하자.

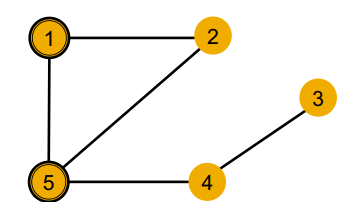
위와 같은 그래프 구조에서 모든 노드가 동일한 변수를 가지고 있다면, 어쩔 수 없이 모델은 local neighborhood structure를 이용해 각 노드를 구분해야 한다.

이때 1번 노드와 5번 노드는 당연히 구분할 수 있다. 두 노드가 가진 이웃 노드의 수(degree)가 2와 3으로 다르기 때문이다.

하지만 1번 노드와 4번 노드는 각 노드의 degree만으로는 구분할 수 없다. 동일하게 2의 degree를 가지기 때문이다. 하지만 이를 2-hop으로 확장해본다면(gnn의 레이어를 2개로 늘린다면) 이웃 노드의 degree는 1 : [2, 3], 4 : [1, 3] 으로 두 노드를 구분할 수 있다. 즉, 레이어를 늘려 모델이 더 노드를 잘 구분하도록 local neighborhood structure를 포착할 수 있다.

하지만 1번 노드와 2번 노드의 경우엔 문제가 복잡해진다. 두 노드가 전체 그래프에서 동일한 위상학적 구조를 가지고 있기 때문에 아무리 hop을 늘린다 해도 두 노드는 구분할 수 없기 때문이다.

그렇다면 gnn의 노드 임베딩은 local neighborhood structure를 어떻게 구분하고, 얼마나 구분할 수 있을까? 구분하지 못하는 상황은 언제 발생할까? 이는 모두 gnn이 local neighborhood structure를 포착하는 방식, 계산 그래프와 관련이 있다.

1-1. Computational Graph

gnn의 각 레이어마다 이웃노드의 정보를 취합하고 이를 가공해서 새로운 노드 임베딩을 생성한다는 점을 상기하자. 이는 결국 gnn은 이웃 노드를 바탕으로 정의된 계산 그래프를 따라서 정보가 흘러가고, 이를 통해 임베딩 레이어가 생성된다는 것을 의미한다.

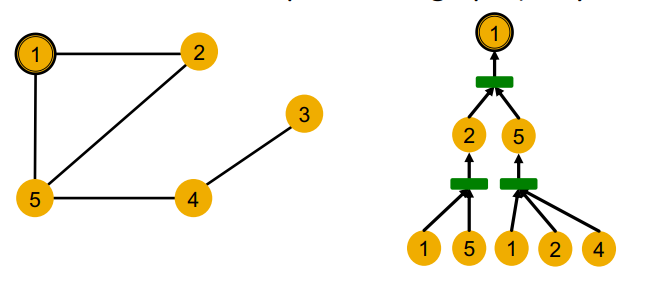
위의 그래프에서 1번 노드를 기준으로 2-hop 이웃노드까지 고려한다고 하면, 결국 2-hop에서부터 시작하여 계산 그래프를 구성하면 1번 노드에 대한 노드 임베딩을 생성하는 과정이 묘사된다.

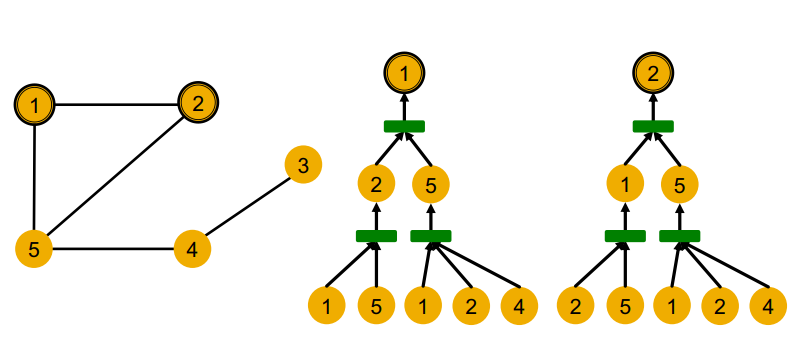
여기서 문제가 발생하는데, 지금 우리는 모든 노드의 변수가 동일하다고 가정하였으므로, 위와 같이 동일한 계산 그래프를 가지는 경우가 생긴다. 이 경우는 두 노드가 위상학적으로 동일한 local neighborhood structure를 가지고 있기 때문이다. 계산 그래프란 local neighborhood structure를 펼쳐놓은 것이기 때문이다.

변수가 동일하다는 점은 모델의 입장에서 각 노드가 노드 자체만으로는 구별할 수 없다는 것을 의미한다. 즉, 우리가 임의로 노드에 id를 부여하고 있지만, 이는 모델에게는 주어지지 않는 정보다. gnn은 노드 id를 직접 참고하지 않기 때문이다.

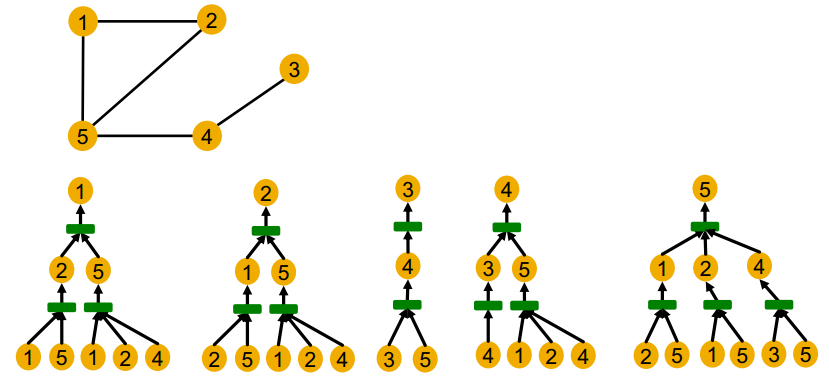
위 노드의 계산 그래프를 모두 그려보면 위와 같은데, 1번과 2번 노드를 제외한 노드들은 다른 local neighborhood structure를 가지므로 다른 계산그래프를 가지고 있는 것을 알 수 있다.

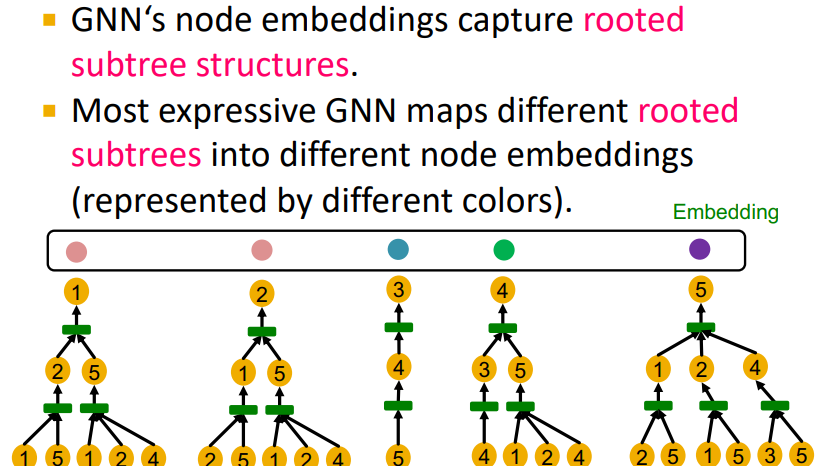
gnn은 결국 각 노드를 root로 한 작은 트리 구조에서 노드 임베딩을 구성한다. 이는 표현력이 좋은 gnn이라면 다른 트리 구조를 가지는 노드에 대해 항상 다르게 임베딩할 것을 의미한다.

1-2. Aggregation function as Injective Function

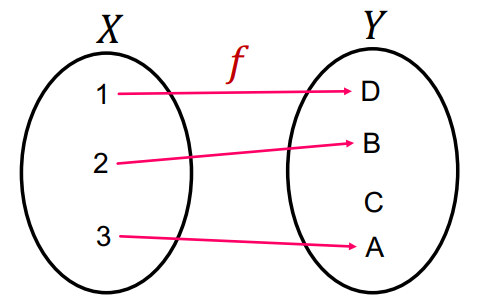
injective function 혹은 단사 함수는 위 그림과 같이 다른 정의역 원소에 대해 다른 치역 원소로 맵핑되는 함수를 의미한다. 직관적으로 이해해보자면 단사함수는 입력값의 정보를 온전히 출력값으로 전달하는 함수라 할 수 있다. 다른 입력에 대해 다른 출력을 내기 때문이다.

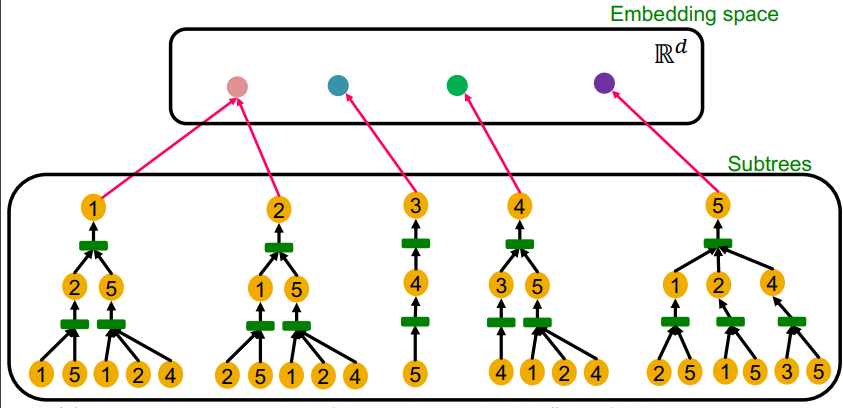
이를 gnn과 연관지어 보면, 가장 표현력이 좋은 gnn이라 함은 계산그래프를 입력으로 하고, 임베딩 벡터를 출력으로 하는 단사함수를 의미한다. 즉, 다른 계산그래프에 대해 각각 다른 임베딩 벡터를 출력하는 함수이다.

좀더 gnn을 자세히 보자면, 동일한 높이를 가지는 계산그래프는 가장 아래단의 잎 노드에서 뿌리 노드까지 반복(recursively)적으로 정보가 처리되면서 구분되게 된다. 예를 들어 위의 그림에서 왼쪽 트리와 오른쪽 트리는 각각의 자식 노드가 다른 이웃노드의 수를 가지기 때문에, 다른 노드라고 구분하는 것과 같다.

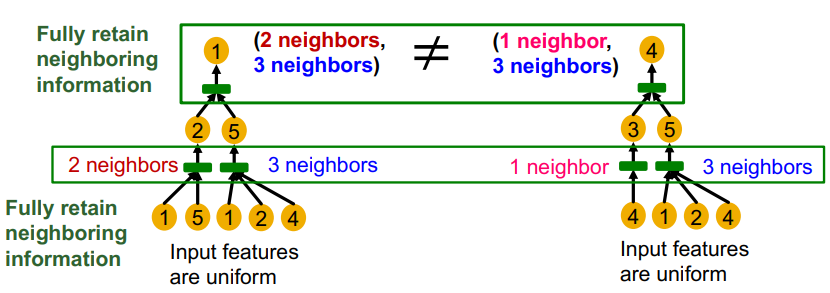
이를 좀 더 자세히 보면, 반복적으로 정보가 처리되는 구간은 aggregation function이다. 즉, gnn의 aggregation function이 단사함수라면, 최대한 이웃노드의 정보를 살리면서 노드를 임베딩하게 되므로, 가장 표현력이 좋은 gnn이 될 수 있다.

2. Aggregation function in GCN & GraphSAGE

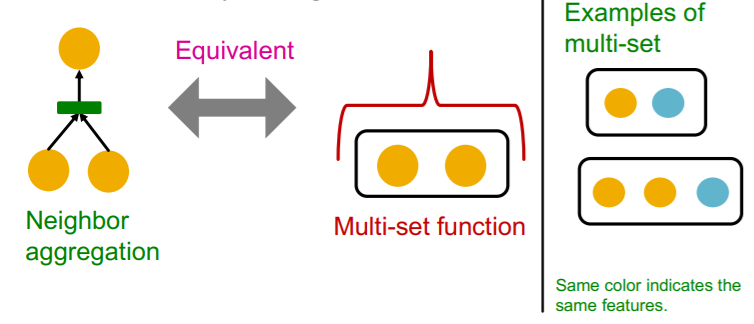
gnn의 aggregation function은 multi-set을 입력으로 하는 함수이다. 이때 multi-set이란, 기존의 집합과 다르게, 원소 간 중복이 허용되는 집합을 의미한다. 즉, 기존의 집합이 [a, a, b]는 [a, b]로 간주했다면, multi-set은 [a, a, b]와 [a, b]를 다른 집합으로 취급한다.
위에서 이야기했듯이, 모든 노드의 변수가 동일하다면, gnn 입장에서는 동일한 원소 여러개를 가지는 multi-set을 입력으로 하는 aggregation function이 될 것이다.

이제, GCN과 GraphSAGE의 aggregation function이 과연 단사함수인지 살펴보도록하자. 우선 두 모델의 aggregation function은 element wise로 다음과 같다.

• GCN : $\text{MEAN}(\{x_u\}_{u \in N(v)})$
• GraphSAGE : $\text{MAX}(\{x_u\}_{u \in N(v)})$

GCN

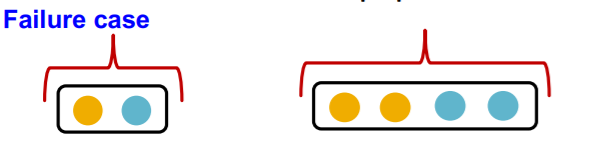
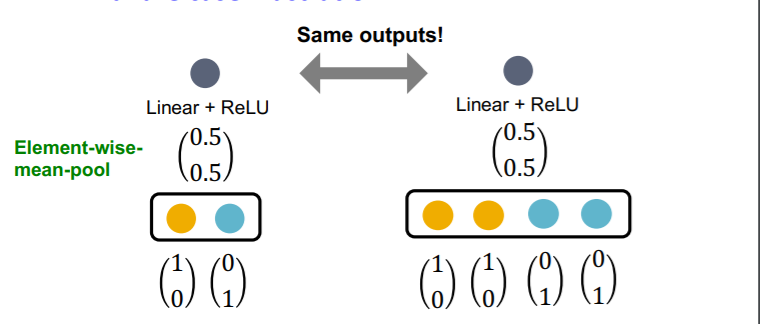
GCN의 aggregation function은 element wise mean을 지나 선형함수와 ReLU 함수를 통과하게 된다. GCN의 aggregation function은 입력 노드의 수를 고려하지 못한다는 문제가 있다. 예를 들어 위와 같이 동일한 이웃 노드가 들어오는데, 그 갯수만 달라지는 경우에 mean의 특성상 동일한 값을 출력하게 된다. 하지만, aggregation function은 multi-set을 입력값으로 한다는 점을 고려하면, 엄연히 다른 입력에 대해 동일한 출력을 내게 되므로, 단사함수가 아니게 된다.

GraphSAGE

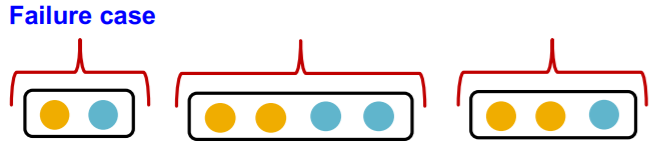
GraphSAGE의 aggregation function은 각 이웃노드의 임베딩 벡터에 대해 MLP를 통과하고 element wise max pooling을 하게 된다. 하지만 이 역시 단사함수가 아니다. 왜냐하면 동일한 원소로 구성된 다양한 multi-set을 구분하지 못하기 때문이다.

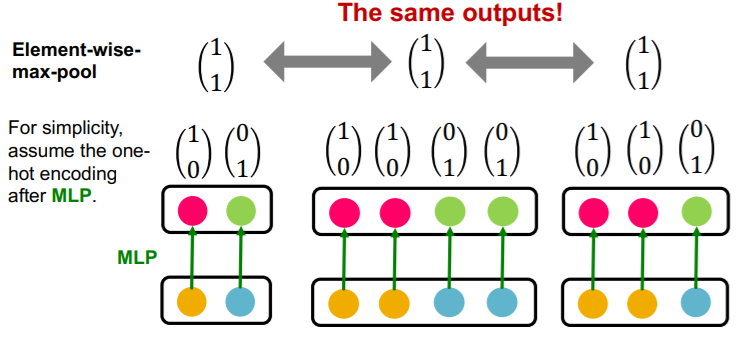
3. Injective Multi-set Function(GIN)

그럼 어떻게 aggregation function을 구성해야 단사함수가 될 수 있을까? GNN의 표현력을 키우는 문제는 결국 aggregation을 어떻게 구성하냐와 관련되어 있기 때문에, 이 질문의 해답을 찾는 것은 중요하다.

우선 왜 GCN이나 GraphSAGE가 단사함수가 되지 못하는지 생각해보면, 입력으로 들어오는 1) 이웃 노드의 갯수를 고려하지 못하거나, 2) 노드의 종류를 고려하지 못하기 때문이다.

그렇다면 이를 구별하여, 각각의 이웃 노드의 벡터를 연산하고, 이를 합치는 방식을 취하면 되지 않을까?

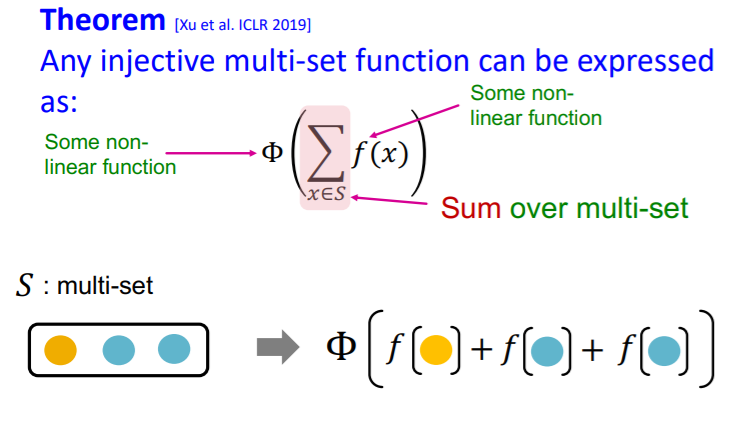
즉, 위 슬라드에서 나온 것처럼 임의의 함수 $\phi, f$를 통해 어떠한 단수함수든 표현할 수 있다. 이때, $f$는 multi-set의 각 원소에 대해 비선형 연산을 가하고, $phi$는 그렇게 처리된 모든 원소의 합에 대해 새로운 비선형 연산을 가하는 역할을 하게 된다.

이때, 어떠한 함수를 $\phi$와 $f$로 쓸지에 대해 1989년에 나온 논문인 Universal Approximation Theorem에 관련된 내용이 있다. UAT의 핵심은 어떠한 연속함수든 간에 충분히 큰 hidden dimension을 가지는 1층짜리 MLP가 근사할 수 있다는 내용이다. 더 자세한 설명은 여기에서 보도록 하자. 즉, 우리가 $\phi$나 $f$에 어떤 함수를 사용해야 적절한지는 모르지만, 1층짜리 MLP를 사용하면 적절히 근사될 것이라 생각할 수 있다. 그렇다면 단사함수인 aggregation function은 다음과 같이 표현이 가능할 것이다(이때, hidden dimension은 100에서 500 사이가 된다.).

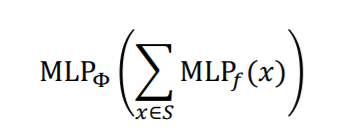
3-1. GIN(Graph Isomorphism Network) with WL Graph Kernel

위의 개념을 사용한 gnn이 GIN이다. 즉, GIN의 aggregation function은 실패하는 경우가 없는 단사함수이며, gnn의 message passing 측면에서 가장 표현력이 좋은 모델이 된다.

재밌는 점은 이전에 배웠던 WL Graph Kernel과 GIN이 비슷한 형태를 띄고 있다는 점이다. WL Kernel에 대한 내용은 이전 수업에서 다룬 적이 있기 때문에 자세히 다루지는 않겠다.

공통점을 중심으로 이야기해보자면, WL Kernel은 핵심은 다음과 같다.
모든 노드에 동일한 컬러 $c^0$을 배정하고, 해시테이블을 이용해 업데이트한다.

이때, 해시 테이블은 조금이라도 다른 입력값에 대해서는 전혀 다른 출력을 내는 함수로서 완전히 단사함수로 동작한다. 또한, k번째 반복에서의 각 노드의 색 변화는 결국 k-hop의 이웃 노드의 정보를 통합한 정보가 될 것이다. 즉, WL kernel은 반복을 통해 k-hop의 정보를 단사함수로 종합하는 함수를 쓴다.

GIN은 여기서 해쉬 테이블을 MLP로 변형하여 사용하는 것이다. 즉, WL kernel처럼 GIN 식을 써보면 다음과 같다($\epsilon$은 학습되는 스칼라이다.).

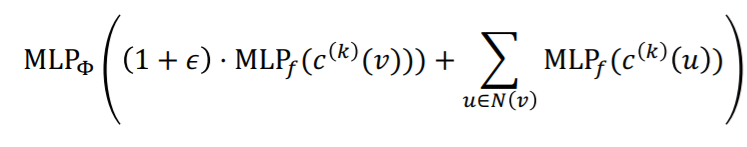
여기서 $\phi$ 안의 첫번째 항은 이전 레이어에서의 본인 노드의 벡터일 것이고, 두번째 항은 이웃 노드의 벡터를 종합한 값이 될 것이다.

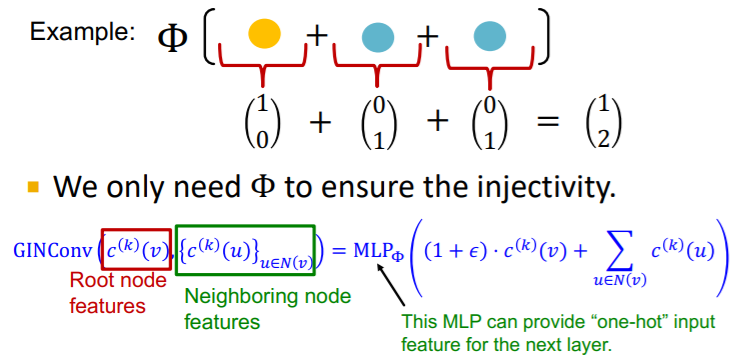
여기서 $\phi$의 역할이 좀 더 직관적으로 다가오게 된다. 만약 함수의 입력이 one hot encoding이라 할 때, $\phi$ 없이 summation 함수만 적용하면 aggregation function은 결국 입력과 다르게 one hot encoding의 형태가 아닌 값을 출력으로 가지게 된다. 즉, 이웃 노드와 본인 노드의 정보를 종합하지만, 출력값이 입력값과 다른 형태를 지니게 되어 레이어를 거듭할 수록 정보가 불안정해질 수 있다. 하지만 $\phi$를 통과함으로써 그 정보가 보존되게 되는 것이다.

3-2. Complete GIN Model

GIN이나 WL kernel 모두 그래프의 내의 노드를 구별할 특별한 변수가 없는 상황에서 사용가능한 기법들이다. 즉, 초기에 GIN은 모든 노드에 대해 동일한 임의의 벡터 $v^0$를 배정하고, WL Kernel은 모든 노드에 대해 동일한 색 $c^0$를 배정한다. 이때, 두 방법론을 정리하면 다음과 같다.

GIN에서 사용하는 aggregation function을 다시 적어보면 다음과 같다.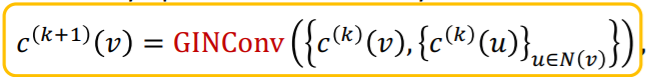
그리고 WL kernel의 업데이트 함수는 다음과 같다.

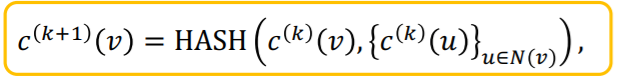
두 함수의 다른 점은 오직 해시테이블이 파라미터로 구성된 MLP로 변경되었다는 점이다.

두 방법론을 비교하면 위와 같은데, GIN이 Wl kernel에 대해 가지는 장점으로는 다음과 같은 것이 있다.

1. 저차원 벡터로 구성되어, 코사인 유사도 등을 이용해 두 노드 간 유사도를 포착할 수 있다.
2. 학습가능한 파라미터로 $\phi$와 $f$가 구성되어 다운스트림 태스크에 맞추어 모델을 fine tuning할 수 있다.

재밌는 점은 결국 GIN이 WL kernel을 근사한 꼴이므로, GIN의 표현력은 WL kernel을 상한으로 가지게 된다는 점이다. 이때, WL kernel은 거의 대부분의 실제 그래프에 대해 효과적으로 적용이 되기 때문에, GIN 역시 가능하다.