Linear Transformer

김재희·2021년 11월 5일

자연어 논문 리뷰

목록 보기

9/12

투빅스 컨퍼런스 주제로 무려 pretrain 모델 만들기를 선정했다... 아직도 이게 맞나 싶긴 하지만 gpu 충분하고 다들 충분히 모델이나 관련 지식이 충분하니까 학부생으로서 할 수 있는 가장 좋은 프로젝트가 될 수 있지 않을까 싶다. 모델의 컨셉은 긴 시퀀스를 입력으로 받을 수 있는 한국어 모델이다. 현재 각자 모델 조사 단계로 longformer나 big bird를 조사해오는 것 같다. 나는 Linear Transformer를 맡아서 리뷰를 해보기로 한다.

0. Intro

기본적인 트랜스포머는 다음과 같은 부분으로 구성된다.

Self Attention
MLP
Cross Attention
Masked Self Attention

위 요소들을 살펴보면, MLP를 제외하면 모두 Attention 구조를 따르고 있음을 알 수 있다. 그런데 attention 구조는 매우 연산량도 많고 역전파를 위해 저장해야 할 정보도 많다. 즉, 시간 복잡도 및 공간 복잡도가 매우 크다.

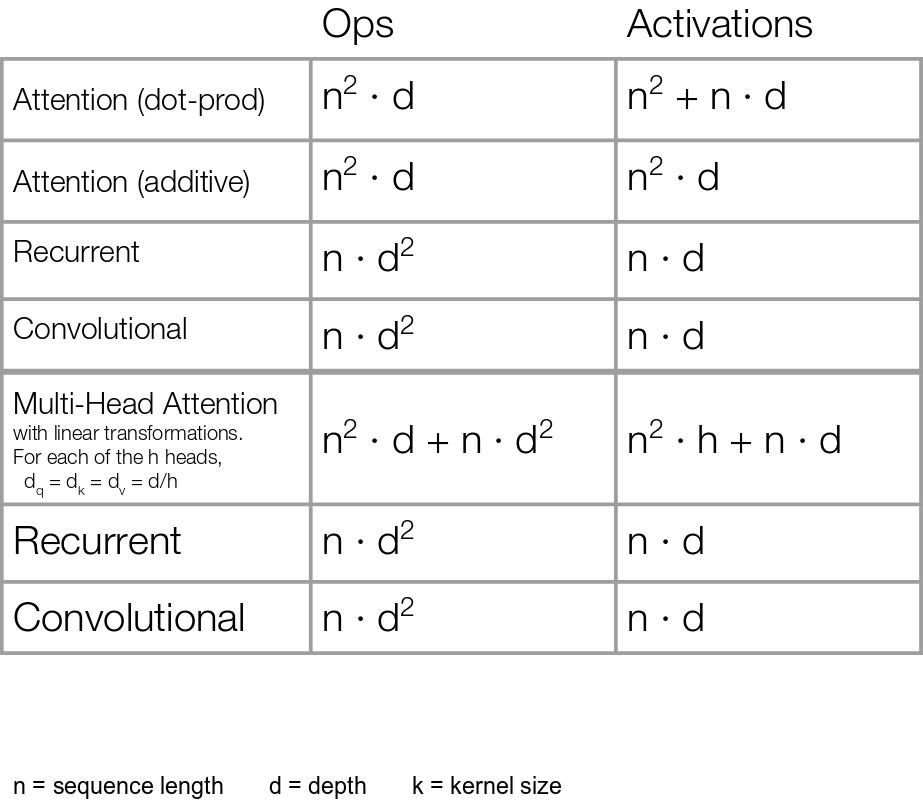
위 표에서 비교하는 것처럼, 기존의 rnn이나 cnn이 차원 수의 제곱에 비례하는 것에 비해, attention 알고리즘은 입력 길이의 제곱에 비례하는 구조를 가지게 됨. 이는 attention을 좀 더 뜯어보면 더 확실하게 알 수 있다.

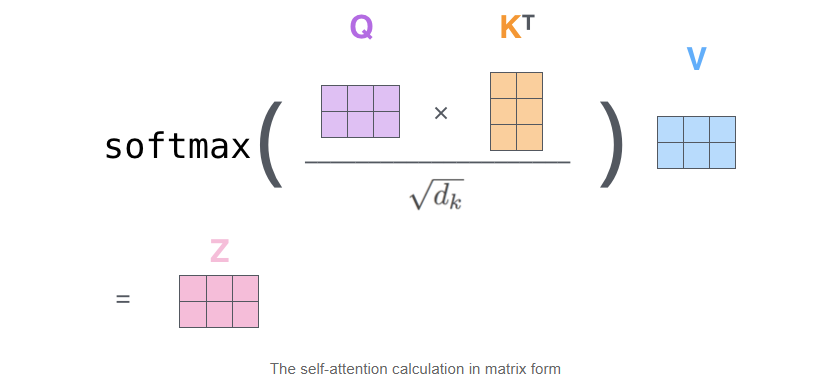
위 그림처럼 q와 k가 시간을 축으로 행렬곱을 통해 연산이 된다.

그런데 이렇게 연산량과 메모리가 많이 필요한 모델이 되면서, transformer 기반 모델들이 가지는 분명한 한계점이 존재하게 된다.

Transformer가 입력 길이 N에 대하여 $O(N^2)$ 의 복잡도를 가지게 되면서, 일정 길이 이상을 연산하기 힘들어진다.

이로인해 Bert는 512라는 길이의 제한이 생기게 되었다. 이게 일반적인 문장들을 처리하는데는 물론 부족함이 없는 길이이기는 하지만, 요약 태스크처럼 토큰 길이가 1000이 넘어가는 일이 종종 있는 태스크를 수행하기에는 부족한 길이인 것도 사실이다. 이로인해서 Bert에 문장 단위로 끊어서 실어서 문장 임베딩을 얻고, 문장 임베딩을 다시 입력값으로 Bert에 넣어서 인코더로 넘겨버리는 등의 괴랄한 방식으로 요약 태스크를 수행하게 된다.

이를 개선하고자 긴 입력을 받을 수 있는 모델들이 연구가 되는데, 최근 들어서 Longformer, Linformer, reFormer, Big Bird 등 다양한 모델이 나오고 있다. 오늘 리뷰할 Linear Transformer 역시 그 일환.

1. Linear Transformer

1-1. Self Attention

해당 논문에서 집중한 점은 소프트 맥스 함수였다. 우선 트랜스포머 내부에서 소프트 맥스 함수 식을 살펴보자.

노테이션은 다음과 같다.

$x$ : 입력 시퀀스 벡터, 한 문장 (N, F)
$Q$ : query (F, D)
$K$ : key (F, D)
$V$ : value (F, M)
$A_l$ : l번째 레이어의 어텐션 함수

여기서 D와 M은 그냥 실제 우리가 가져오는 값인 V와 어텐션에 이용하는 Q, K를 다른 차원으로 설정한 것에 불과하다.

Q = xW_Q \\ K = xW_K \\ V = xW_V \\ A_l(x) = V' = \text{softmax}({ZK^T \over \sqrt{D}})V

여기서 $V'$ 는 모든 시퀀스를 통채로 이야기하고 있는데, i번째 시퀀스만 떼어서 다시보면 다음과 같다.

V' = {\sum^N_{j = 1} \text{sim}(Q_i, K_j)V_j \over \sum^N_{j = 1}\text{sim}(Q_i, K_j)}

즉, 임의의 유사도 함수 sim을 정의하고 이에 맞추어서 어텐션을 수행하게 된다. 여기서 핵심은 어텐션은 소프트맥스 함수가 필수가 아니라는 점이다. 즉, 우리는 i번째 토큰을 기준으로 할때, 각 시점의 토큰들의 K와 i번째 토큰의 Q의 유사도를 비교하고, 상대적으로 유사한 정도에 맞추어 j번째 토큰의 V를 가중합하게 된다. 이때 다른 토큰과 비교하여 j번째 토큰이 상대적으로 얼마나 유사한지 측정하기 위해서 분모가 삽입되게 되는 것이다. 즉, 소프트 맥스 함수가 어텐셔 매커니즘의 필수요소는 아니다. 위 식에서 $sim(Q, K) = exp({Q, K^T \over \sqrt{D}})$ 으로 하면 우리가 알고있는 트랜스포머 모델이 된다. 그런데 얘는 역시 내적을 하다보니 연산량이 많다...

1-2. Kernel Function

그렇다면 유사도 함수 sim이 가져야할 조건은 무엇일까? 아래와 같은 식으로 표현이 가능하다.

sim(x, y) = sim(y, x) :\mathop{\mathbb{R}}^{2\times F} \to \mathop{\mathbb{R}}_+

말로 풀어보자면, 유사도 함수는 1. 대칭이어야 하고, 2. 양수인 스칼라를 출력으로 해야 한다.

여기서 유사도 함수가 두 벡터를 입력으로 하여 스칼라를 출력한다는 걸 생각해보면, 일종의 커널 함수라고 볼 수 있다. 즉, x, y를 입력으로 해서 고차원으로 맵핑하고, 그 값을 내적하는 과정을 내적 후 연산하는 과정으로 변환했다고 보는 것이다.
그렇다면 유사도 함수는 다음과 같이 표현할 수 있을 것이다.

sim(x, y) = \phi(x)^T\phi(y)

이렇게 표현을 바꾸면, 아래와 같이 어텐션도 표현을 달리 할 수 있게 된다.

V'_i = {\sum^N_{j =1} \phi(Q_i)^T \phi(K_j) V_j \over \sum^N_{j =1} \phi(Q_i)^T \phi(K_j)}

그런데 여기서 summation 안에 있을 필요가 없는 항을 빼면 연산량이 또 줄어든다.

V'_i = {\phi(Q_i)^T \sum^N_{j=1}\phi(K_j)V_j^T \over \phi(Q_i)^T \sum^N_{j=1} \phi(K_j)}

이제 Linear Transformer의 식이 완성되었다. 기존의 트랜스포머의 어텐션 식은 소프트 맥스를 계산하기 위해 $O(N^2)$ 의 시간복잡도를 가질 수 밖에 없었지만, 위의 식으로 바뀌면서, summation 내부의 값들은 한번만 계산하면 매 토큰마다 사용할 수 있게 되었다. 즉, $O(N)$ 으로 시간복잡도가 줄었다! 계산과정 자체가 줄어든 것이기 때문에 메모리 사용 측면에서도 기존의 모델보다 동일하게 줄어든 것 역시 알 수 있다.

이때 $\phi$ 로는 활성화 함수 elu를 사용한다고 한다. 식은 다음과 같다.

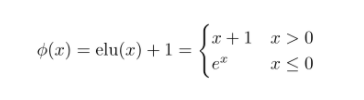
여기서 relu가 아닌 elu를 사용한 이유는 0보다 작을 때도 그래디언트를 전달하고 싶었다고 한다.

1-3. Casual Masking

이전까지 인코더에서 쓰이는 self attention에 대해 살펴봤다면, 이제 디코더에서 쓰이는 masked self attention을 살펴보도록 하자. 이 사람들이 이쪽에서 식을 꽤 많이 바꿔서, 이름도 casual masking이라고 바꿨다.

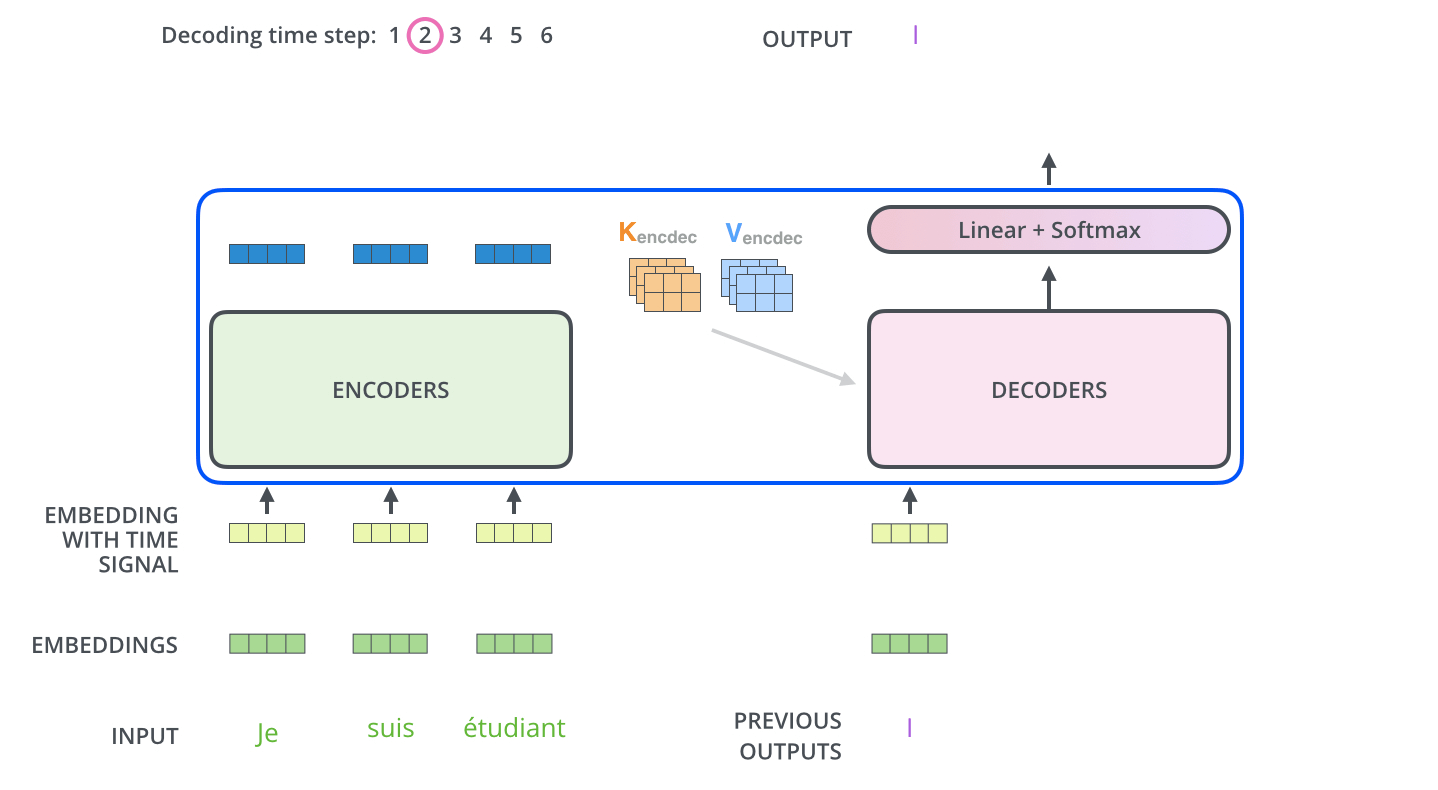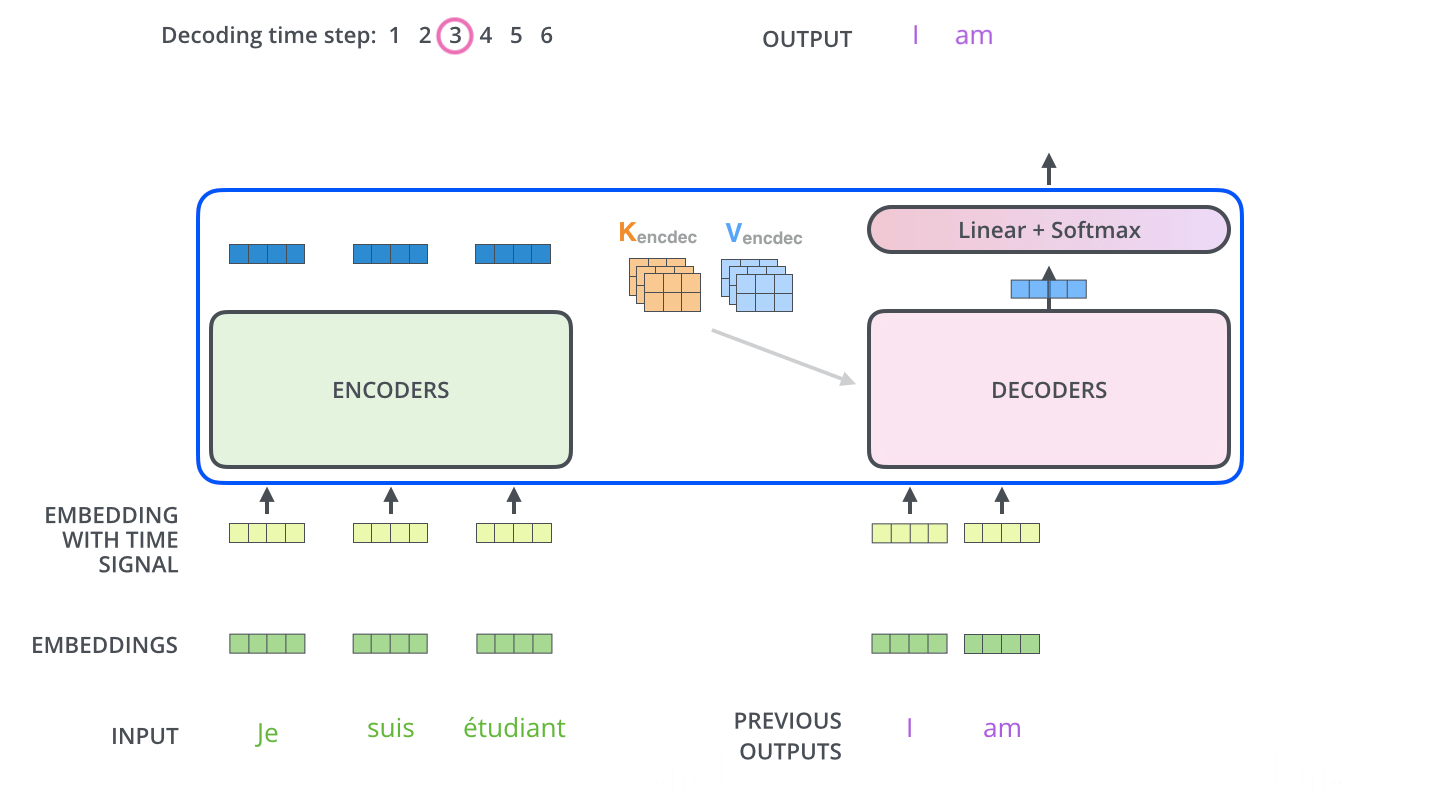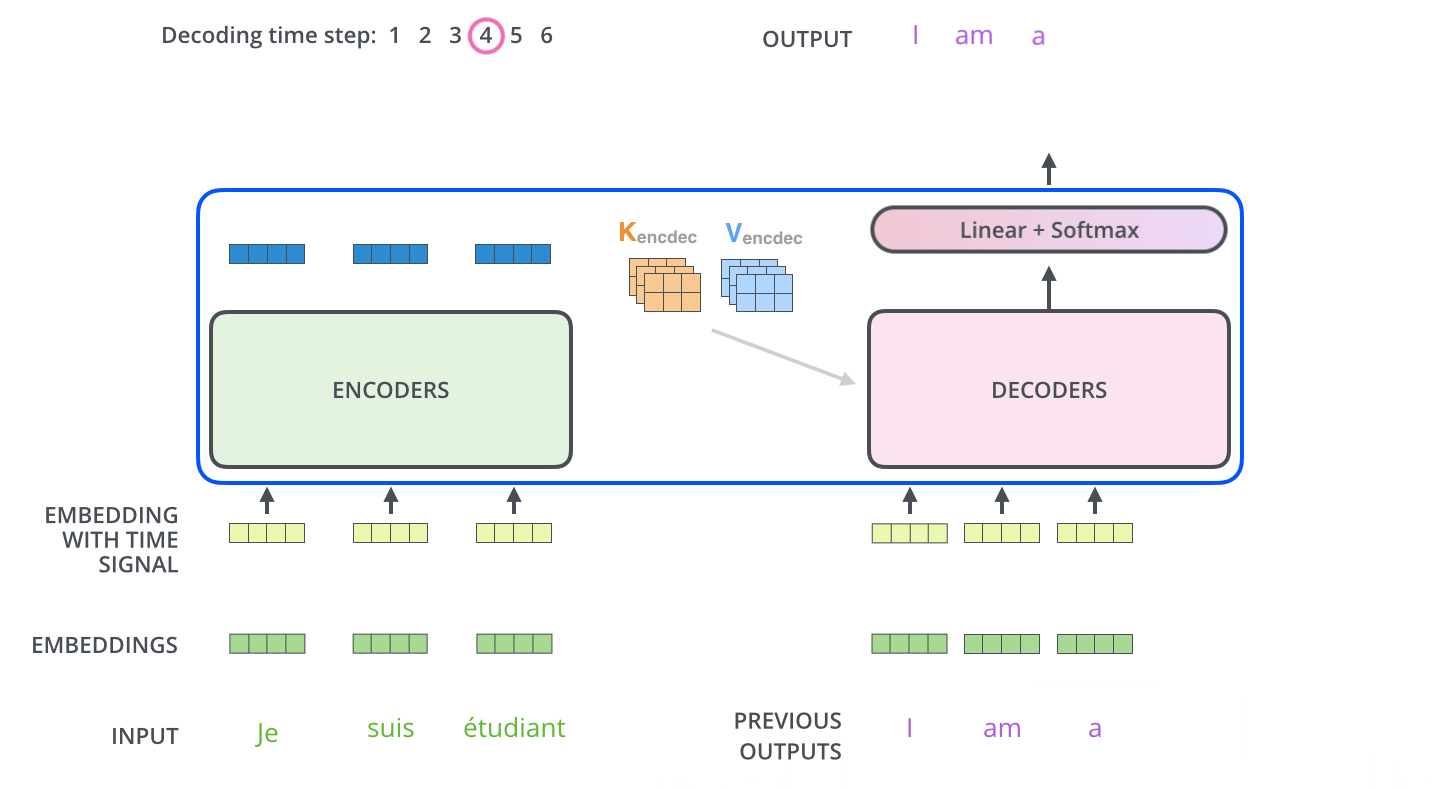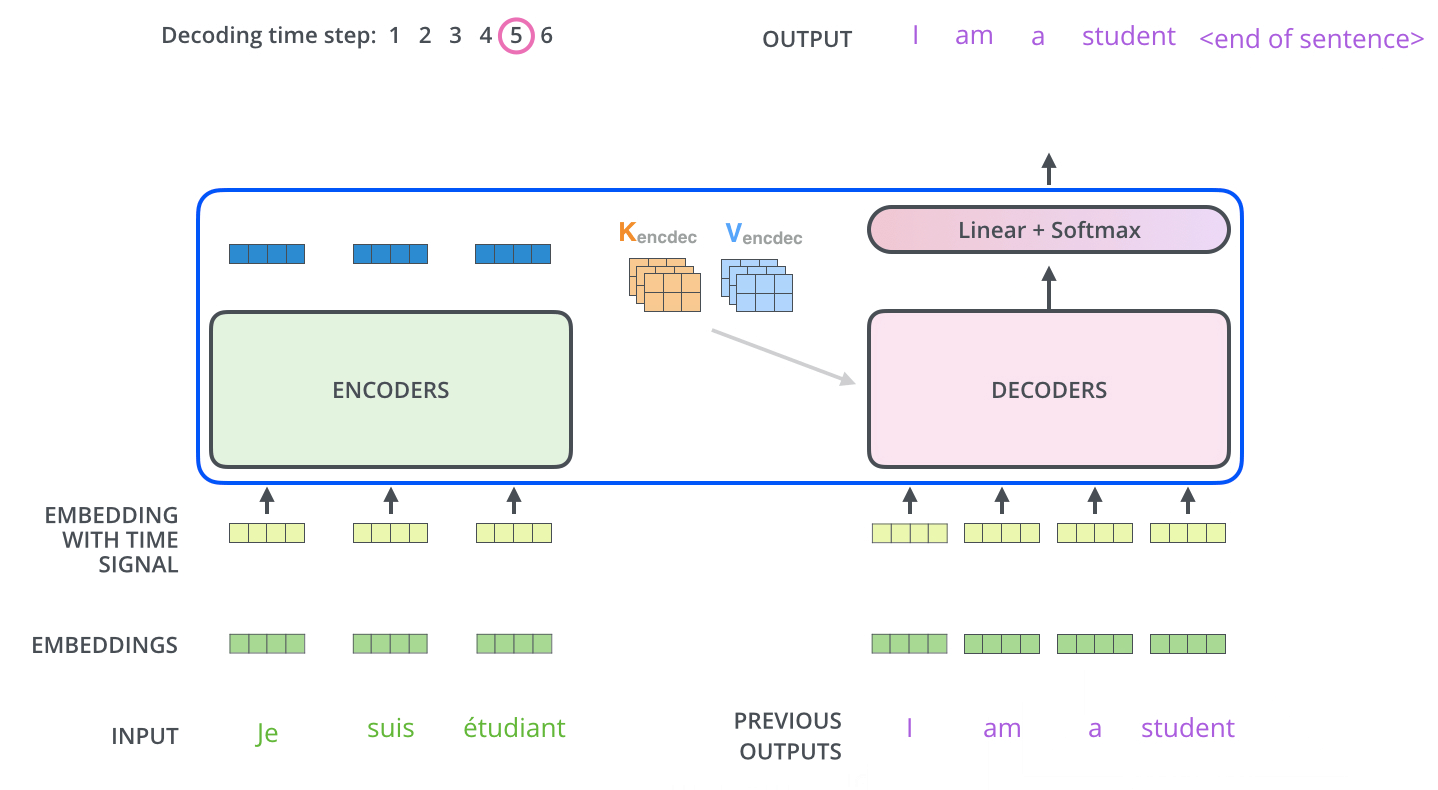
디코더는 위에서 보는 것처럼 이전 시점의 예측값이 입력값이 되고, 이전 시점까지 생성된 토큰들을 바탕으로 attention이 이루어지게 된다.

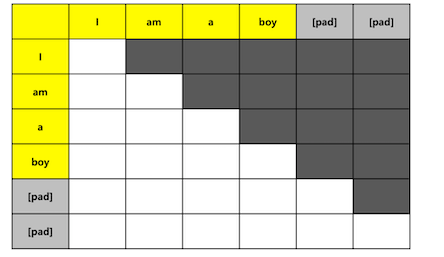
그래서 어텐션도 위 그림처럼 대각하 성분만 남은 어텐션을 수행해야 한다. 그런데 이 논문에선 이런 절차를 다 없애버렸다. 위의 식에서 summation의 범위만 바꿔서 이를 해결하고 있다.

V'_i = {\phi(Q_i)^T \sum^i_{j=1}\phi(K_j)V_j^T \over \phi(Q_i)^T \sum^i_{j=1} \phi(K_j)}

바뀐 점은 하나다. 가져오는 범위가 1부터 i까지로 바뀐 것이다. 이게 무슨 큰 변화냐 싶을텐데, 연산량의 측면으로 가져오게 되면 큰 변화가 된다. 위의 식을 좀 더 뜯어서 보자.

S_i = \sum^i_{j =1}\phi(K_j)V_j^T\\ Z_i = \sum^I_{j=1}\phi(K_j)\\

위 두 항으로 치환하면 어텐션 식이 간단해진다.

V_i' = {\phi(Q_i)^TS_i \over \phi(Q_i)^TZ_i}

여기서 중요한 점은, S랑 Z는 매 시점마다 1부터 i까지 계산할 필요가 없다는 것이다. 다음과 같은 점화식으로 S와 Z가 표현이 가능해지기 때문이다.

S_i = S_{i-1} + \phi(K_i)V_i^T\\ Z_i = Z_{i-1} + \phi(K_i)

이렇게 변하면 이제 더이상 매 시점마다 시퀀스 길이만큼 연산을 수행할 필요가 사라진다. 즉, 디코더에서도 $O(N^2)$ 에서 $O(N)$ 으로 시간복잡도가 줄어들게 되는 것이다.

1-4. Transformers are RNNs

이 파트는 솔직히 조금 과한 것 같기는 한데, 모델이 돌아가는 구조를 전반적으로 보자면 RNN과 Linear Transformer가 동일하다는 이야기를 하고 있다. 즉, Linear Transformer가 디코더에서 쓰일 때를 살펴보면, 다음과 같은 요소들로 연산된다.

$\phi(Q_i)$ : 이번 시점의 입력값
$S_{i-1}, Z_{i-1}$ : 이전 시점까지의 정보
$\phi(K_i)V_i^T, \phi(K_i)$ : 이번 시점의 정보 중 S와 Z에 실을 정보

RNN이 매 시점의 입력을 받아서, 이 중 다음 시점으로 흘려보낼 정보를 hidden state에 담는다는 점에서 위 구조가 RNN과 유사하다고 이야기 하고 있다. 그래서 논문에서는 식도 아래와 같이 다시 구성한다.

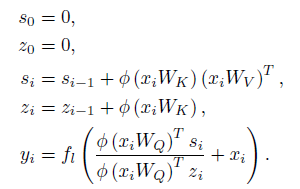
사실 그렇게 와닿는 이야기는 아니다.

Casual Masking의 알고리즘은 다음과 같다.

1-5. Experiment

실험에서는 바닐라 트랜스포머(softmax), Reformer(lsh), 본인 모델(linear)를 비교한다.

시퀀스 길이에 따른 연산량 및 메모리 사용량 비교

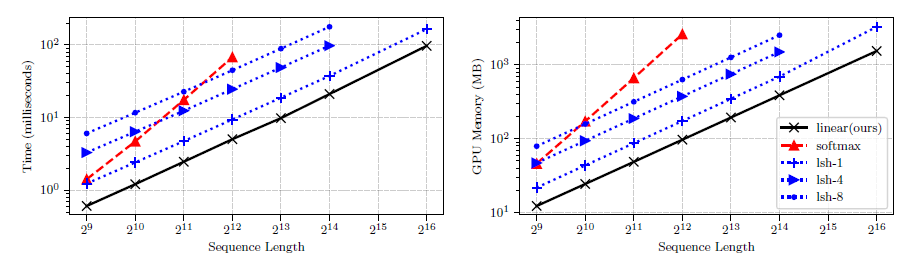
y 축이 로그 스케일링된 상태임을 감안하면 꽤 차이가 크다.

부호 복사 태스크
임의의 토큰을 이용해서 입력받은 토큰을 복사하는 태스크를 수행했다. 즉, 언어 모델처럼 discrete한 변수를 다룰 수 있는 능력을 보고자 한 것 같은데, 연구자 중에 NLP하는 사람이 없었는지 왜 NLP 태스크를 안했는지 의아하다.

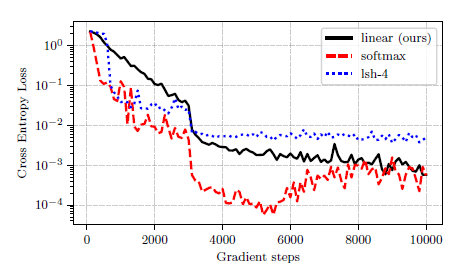
결과적으론 바닐라 모델과 비슷한 성능을 보이고, reformer보다 좋은 성능을 보인다. 사실 요새 실험 결과는 이 모델 저 모델 다 가져다 비교하는데, 세 모델끼리 비교하는게 맞나 싶다.