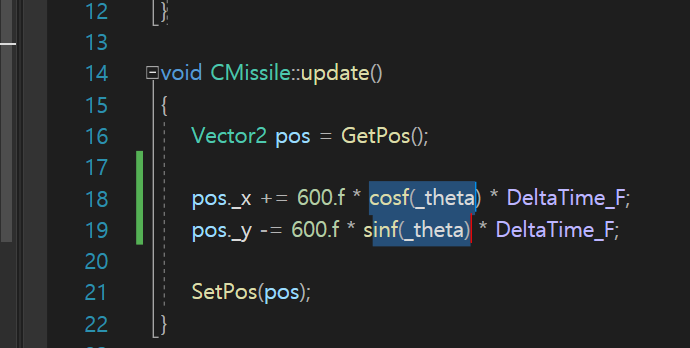
내가 지금 부여한 id에 따라서

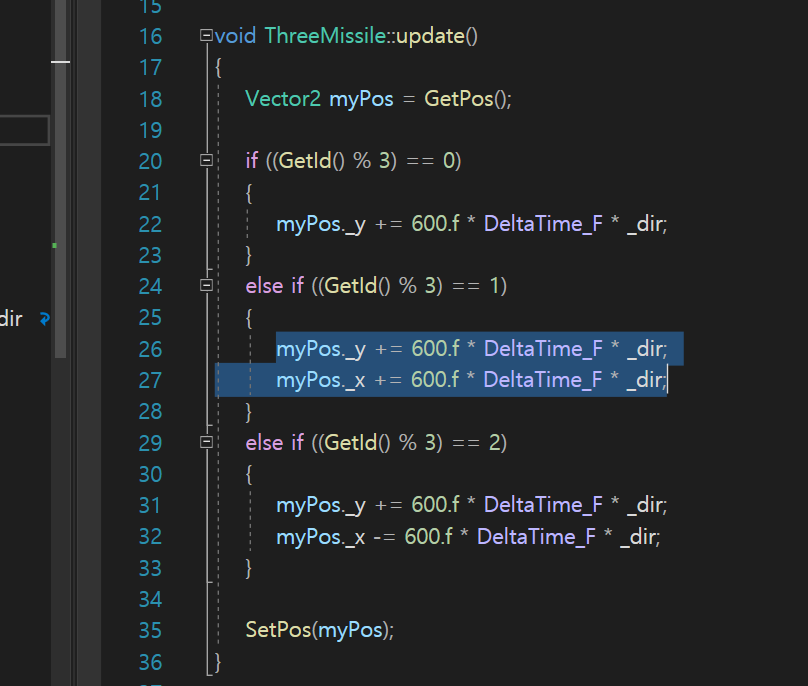
현재 x, y축으로 이동하게 했다.

600.f 라는 값 자체가 이동속도의 개념으로 정의해놓은것이다.

이렇게하면 초당 600을 이동을 할까?

만약 초당 1이라는 값을 이동하고 싶다면은 (1초에 1만큼)

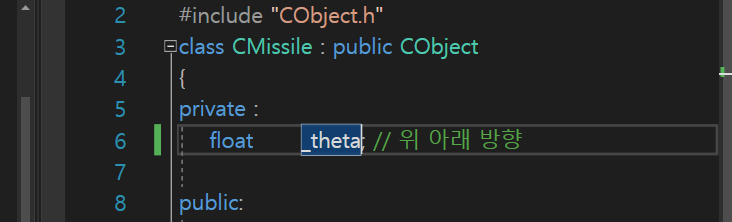
한프레임에는

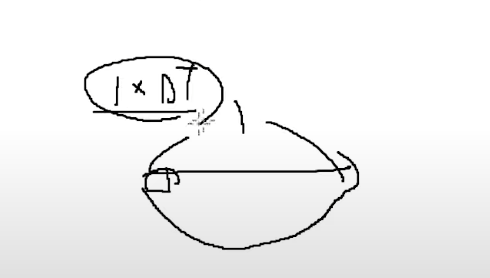
그림의 네모칸 프레임(한 프레임) 동안은 1 * DT만큼 이동시킬 것이다.

이렇게 했을 때 결과적으로 1초 뒤에 1 이동한 셈이 된다.

대각선 방향 ❗

그런데 내가 대각선 방향으로 1을 이동하고싶다고해서

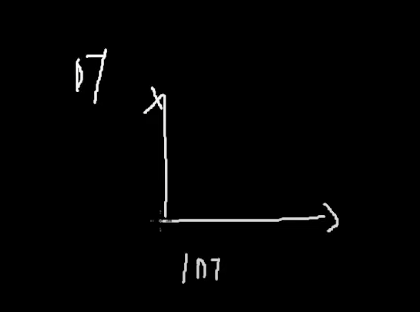
가로로 1 DT이동하고 세로로 1 DT이동 해서

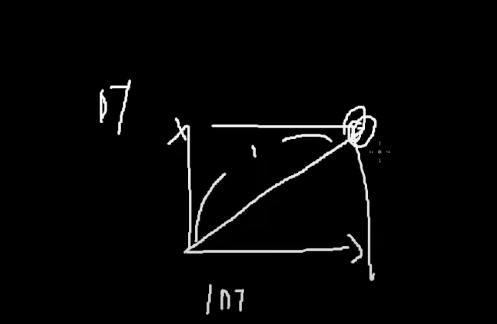
현재 이 위치에 있다면은 이게 1초뒤에 1을 이동한 것일까?

루트 2 이동함.

따라서 '이동속도'라는 것은 어느 방향으로 이동하든지 간에 이동방향의 속도를 말하는 것이다.

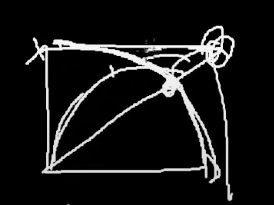
사실은 원을 그려서 해당 점 부분까지 이동했어야 했다.

이런거 알려면 '삼각함수' 알아야한다.

삼각함수 ❗❗❗

삼각함수에서ㅏ 사용하는 '각도'의 단위는 '호도법' == '라디안'이다.

'라디안' : 실제 계산에서 사용되는 값.

라디안

호의 반지름과 호의 '비율'값이다.

• 파이 : 원주율

원주율이 뭐임?

'원'의 정의를 알아야한다.

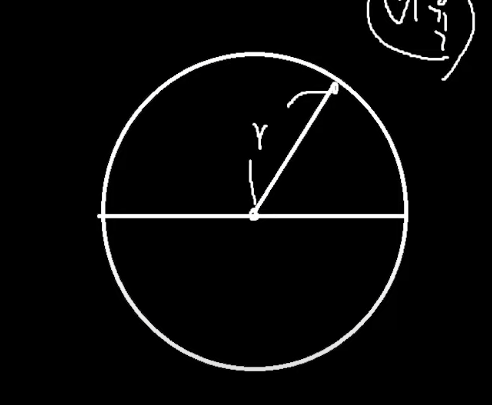
이게 원임. 중심으로부터 일정한 r 이라는 값만큼 떨어진데까지의 거리를 다 합한녀석임.

원주율이란 원의 '지름'과 '원의 전체 둘레 길이'의 '비율'이 있다.

그래서 원의 크기가 어떻든지간에

원의 지름을 알면 거기에 3.14를 곱하면 전체 원의 둘레의 길이가 나오더라...이다.

그래서 내가 지름만 구한다면 전체 둘레의 길이를 구할 수 있다.

ㅇㅇ.

r 의 입장

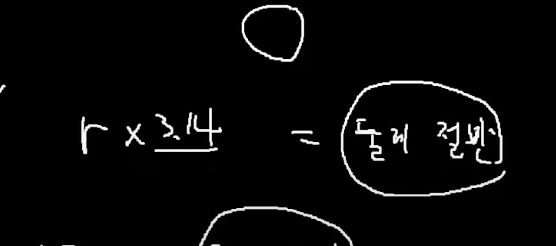
반지름 * 3.14 => 둘레길이 절반 나옴. => 비율에 따라서...

그래서

호도법의 라디안

반지름과 원의 둘레사이의 비율값을 얘기하고자 하는 것이 바로 호도법의 '라디안'이다.

파이를 반지름에 곱하면 둘레의 절반이 나오니까

이것을 각도 => 한바퀴의 절반 으로 보겠다. 그래서

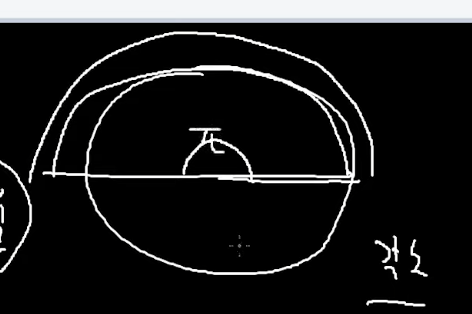
이 각도를 π로 보겠다.

π라는 것은 구체적인 값이다.

π 이게 전체 각도의 절반을 의미를 한다..

반지름 * π 하면 => 둘레절반 길이 나옴.

그래서

반지름과 둘레 사이의 '비율'을 곧 '각도'로 보는게 '라디안'이라는 '각도'이다.

라디안

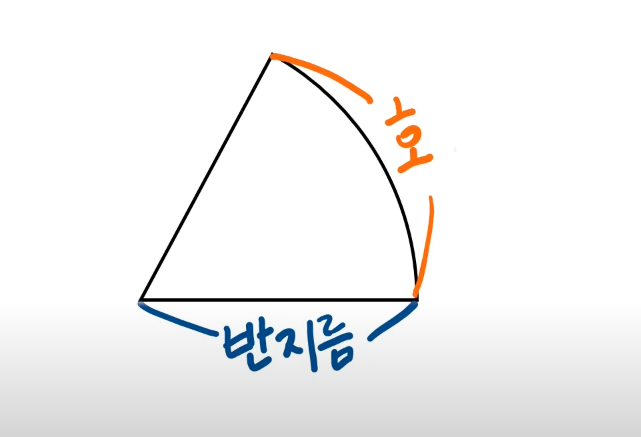
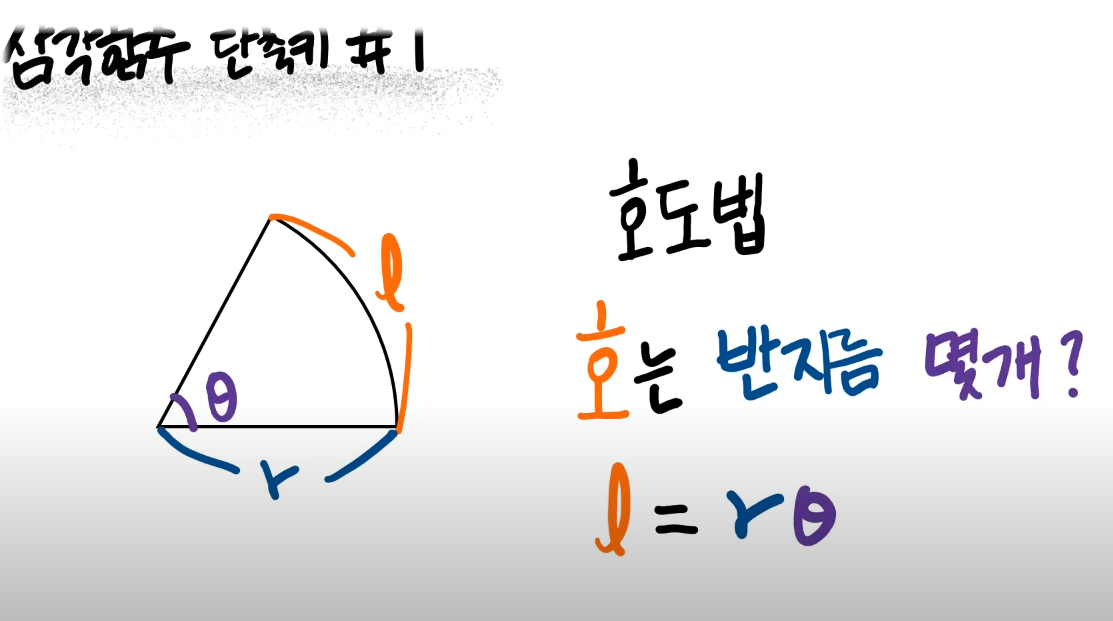
부채꼴의 호를 이용해서 각도를 나타내는 방법이 '호도법'이다.

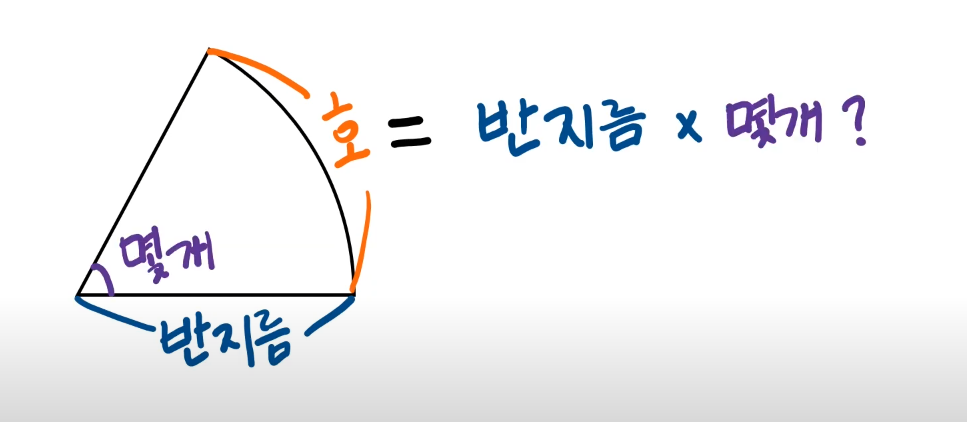
'호'는 반지름 몇개?

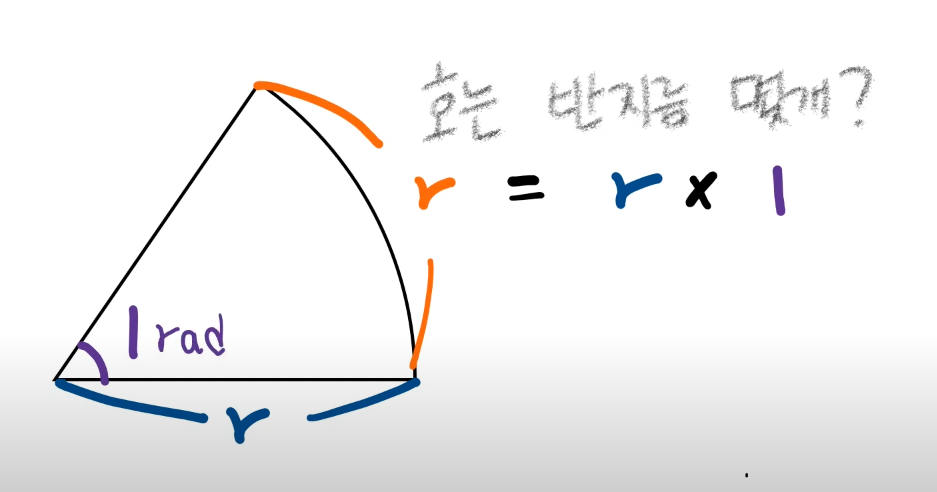
반지름의 길이가 r이고 호의 길이도 r 이라고하면은

호는 반지름 몇개인가?

호 = 반지름 * 몇개?

r = r * 1 => 호는 반지름 1개이다. 이것을 1 라디안 이라고한다.

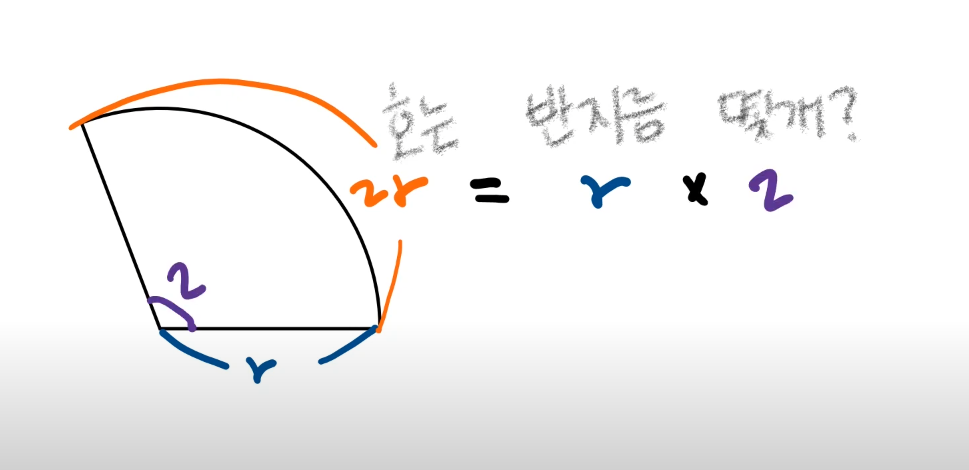
호는 2r일때 호는 반지름 몇개? => 2개이다. 그래서 2라디안 이다.

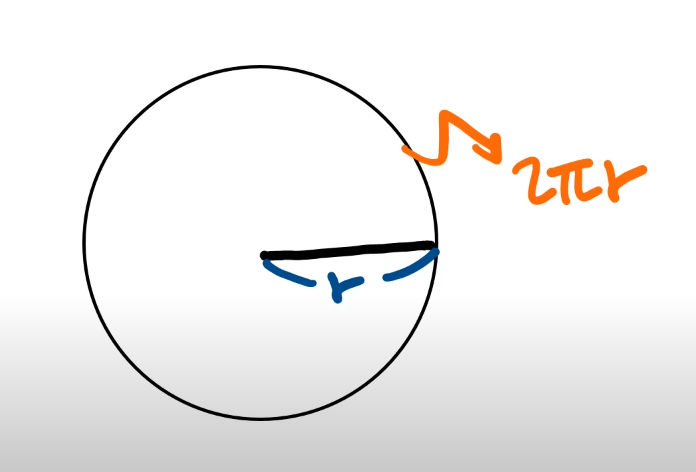
원 둘레의 길이는 2πr이다. 이때 라디안은?

호가 2πr 일때 반지름 몇개고? => 2π개이다.

이떄 각도는 2π라디안이다.

그래서 호도법에서 360도는 2π라디안으로 표시한다.

그래서 일반적으로 호도법으로 표기할때 rad(라디안 표시)를 생략한다.

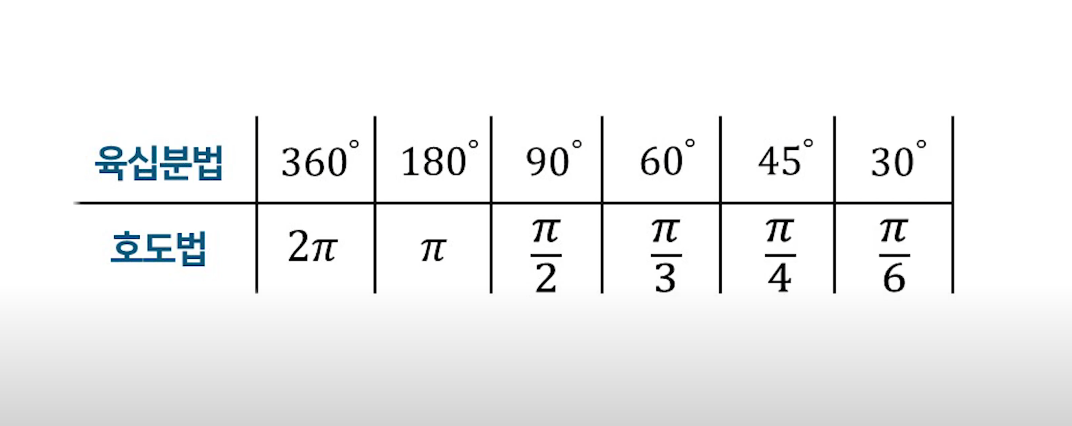
그래서 육십분법으로 보면 호도법으로 라디안 값은 이렇게된다.

이런 각도들을 '특수각'이라고한다.

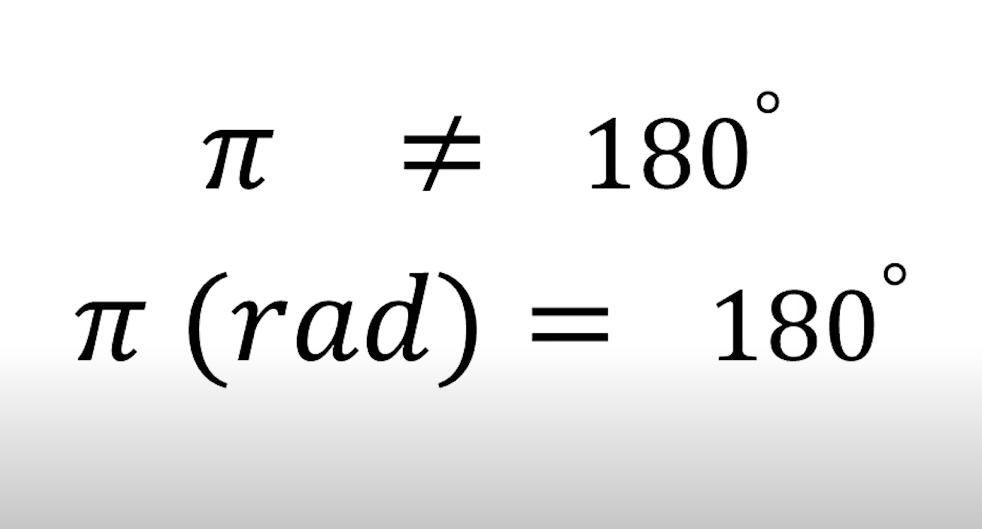
π가 180도라는게 아니라 π (rad) 가 180도 라는 것이다.

그래서

반지름과 둘레 사이의 '비율'을 곧 '각도'로 보는게 '라디안'이라는 '각도'이다.

이게 라디안 이다.

그렇다면 라디안은 '각도'인데 1라디안은 몇도 인가?

π 라디안은 몇도일까? => 180도 이다.

반지름 * π = 반 둘레의 길이

1라디안은? => 57도쯤 된다.

1라디안의 뜻?

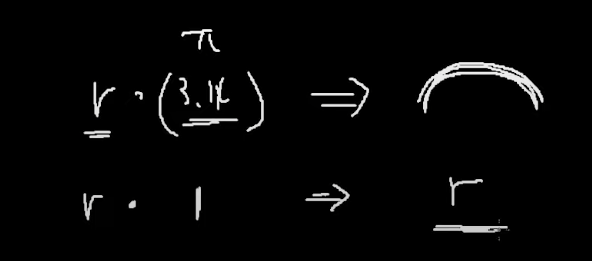
r이 나오는데 이게 호의 길이를 나타낸다.

라디안이 반지름과 호의 길이의 비율값이라며...

삼각함수

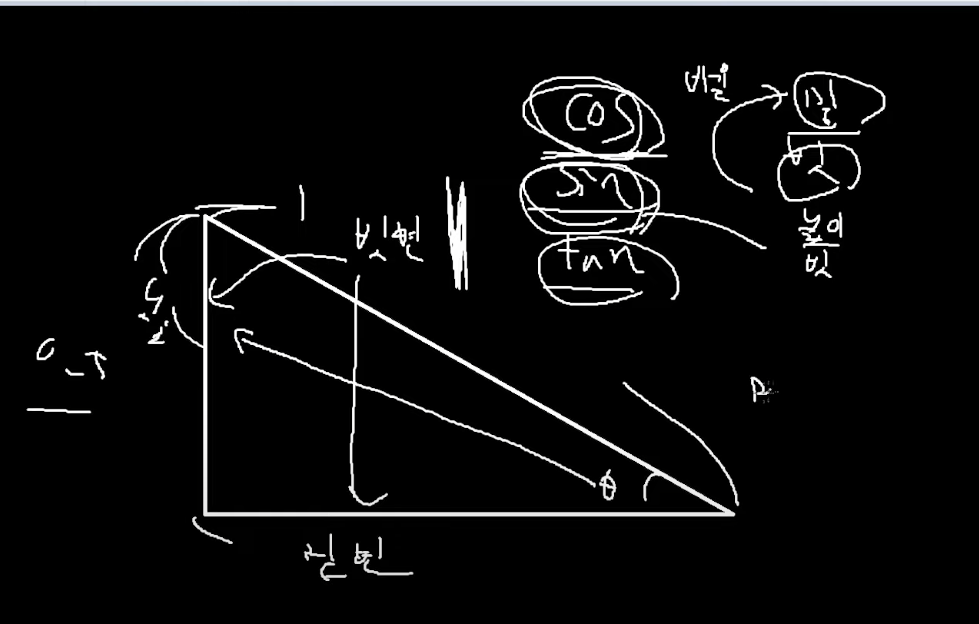
이녀석도 비율인데

• cos : 높이 / 빗변 비율

• sin : 밑변 / 빗변 비율

• tan : 높이 / 밑변 => 기울기

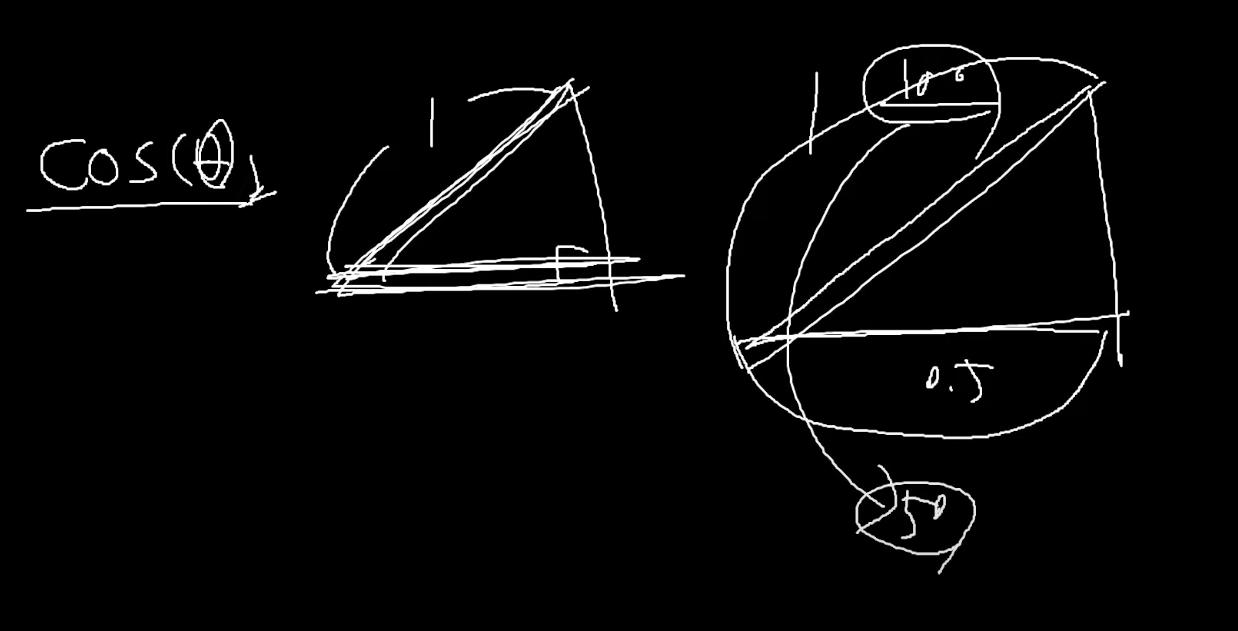
이렇게 cos값 추론 가능하다. 빗변의 길이로 밑변 길이 구할 수 있다.

반지름이 r일때

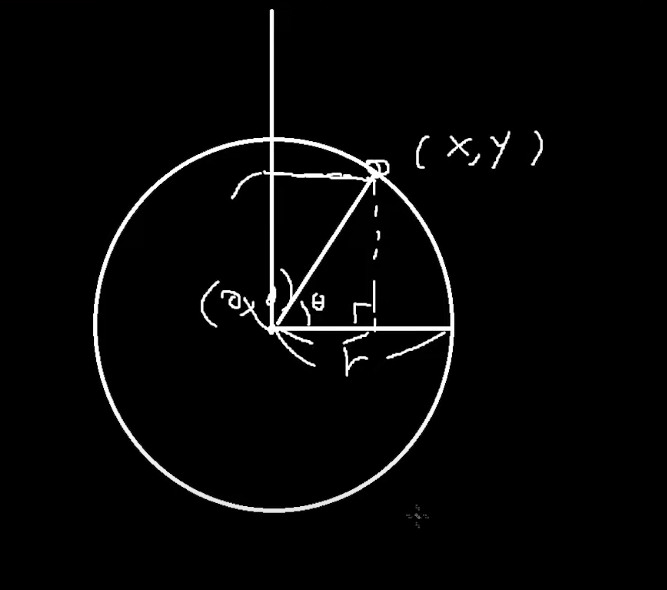
좌표는 (cos θ, sin θ ) 이다.

반지름의 길이가 1인 원을 '단위원'이라고한다.

90도일 경우

sinθ : 1이 되어버린다.

밑변을 0을 향해서 가기 때문에 cos θ : 0이 되어 버린다.

가야할 곳

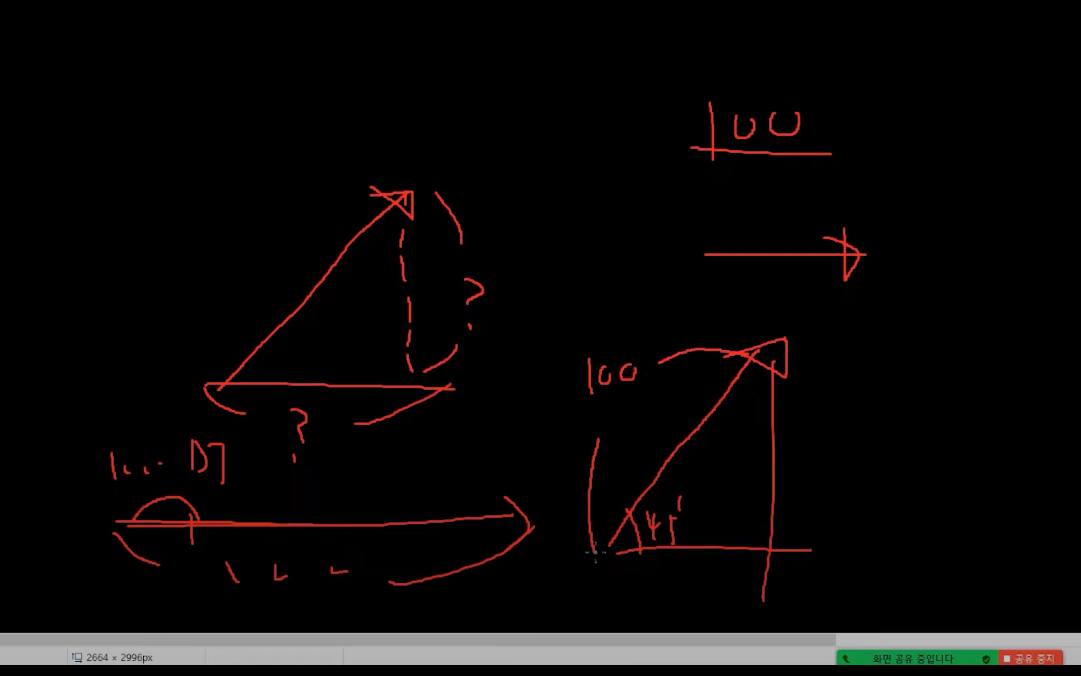
45도 방향으로 100만큼 가야한다

최종 목적지의 좌표는 (cos45, sin45) 이다.

단위원 기준으로 반지름이 1일때

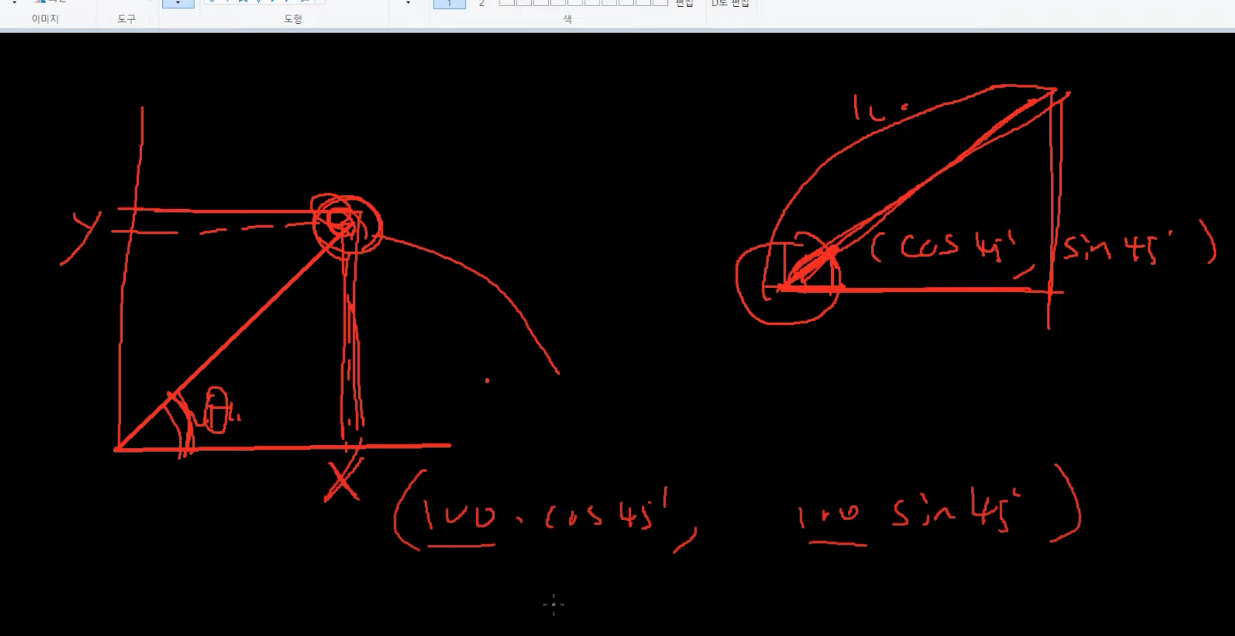
좌표가(cos θ, sin θ )인데 만약에 반지름이 100일 경우

삼각형의 닮음 이기 때문에

(100 cos θ, 100 sin θ) 이 된다.

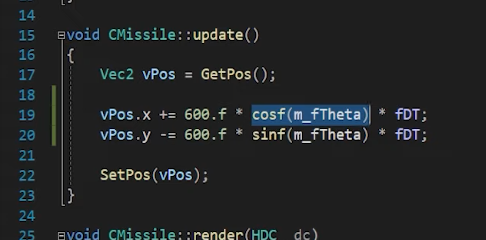
그래서 x축으로 이동해야하는 거리는

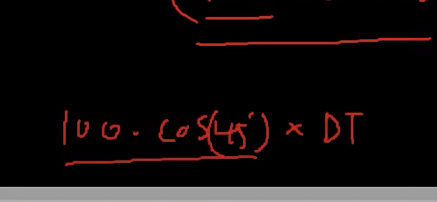
이동속도가 100이라 했을 때 이번 프레임에서는

100 cos45도 DeltaTime만큼 움직여야한다. 이게 매프레임 마다 움직여야할 거리이다.

각도가 이동방향이다.

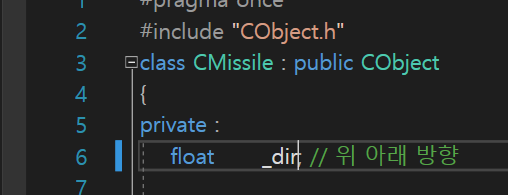
그래서 이제 각도를 이동방향으로 정해주도록 하자.

이렇게

PI

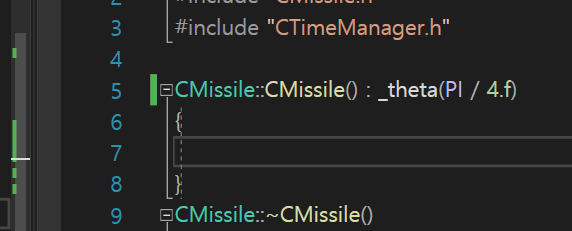
파이라디안 은 180도라 했다. 라디안을 생략해서

파이 = 180도이다.

그러면 45도는 π / 4 이다.

근데 공 날리면 아래로 날아간다.

윈도우 좌표는 위 아래가 뒤집혀 있다.

기초수학 2

우리가 이런식으로

각도를 사용하는 것보다 이제 좋은게 벡터를 사용하는 것이다.

접근성도 쉽고 좋은 방법이 '벡터'임.

벡터

Vector는 Scalar와 대비된다.

Scalar는 '값'을 말하는 것이고 Vector는 '크기'를 말한다.(방향)

Vector가 (3, 2)를 가르킨다고 하면은

방향이 3, 2를 가르키고

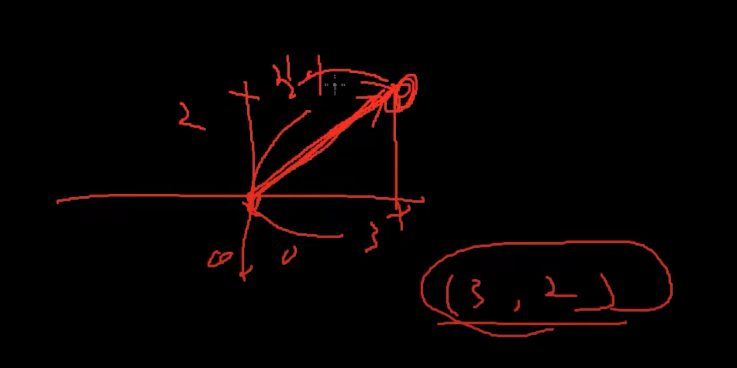
'길이'가 '크기'를 말한다.

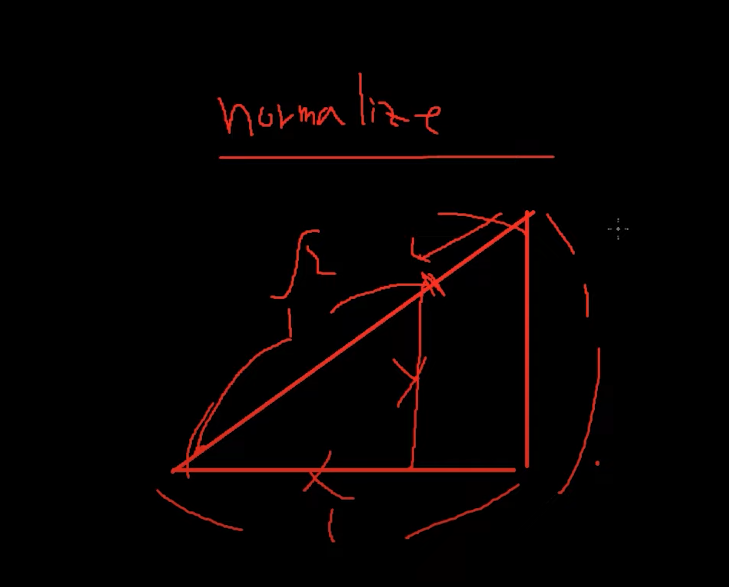
그래서 가로 세로 가 각각 1일때 빗변의 길이를 1로 잘랐을때의 가로 세로의 길이가 무엇인지 구하는게

'벡터의 정규화'라고한다. => Normalize

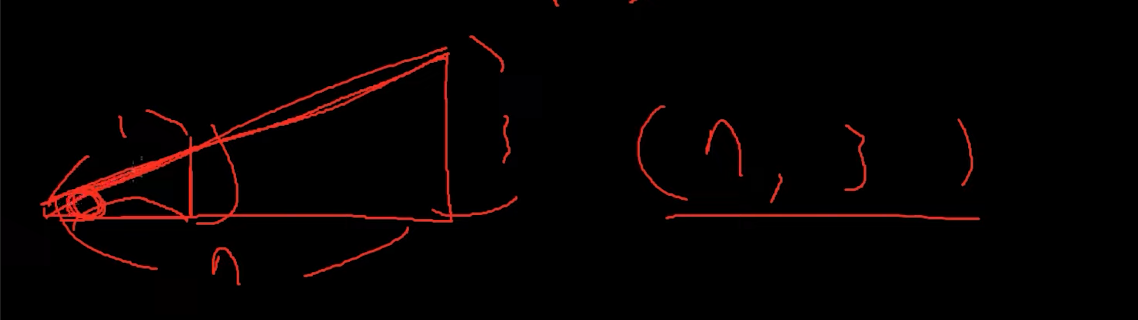
(7, 3)을 정규화 해봐라 => 할게 많다.

그래서 정규화 공식이 있다.

벡터 정규화 공식

본인의 길이값으로 나누어 준다.

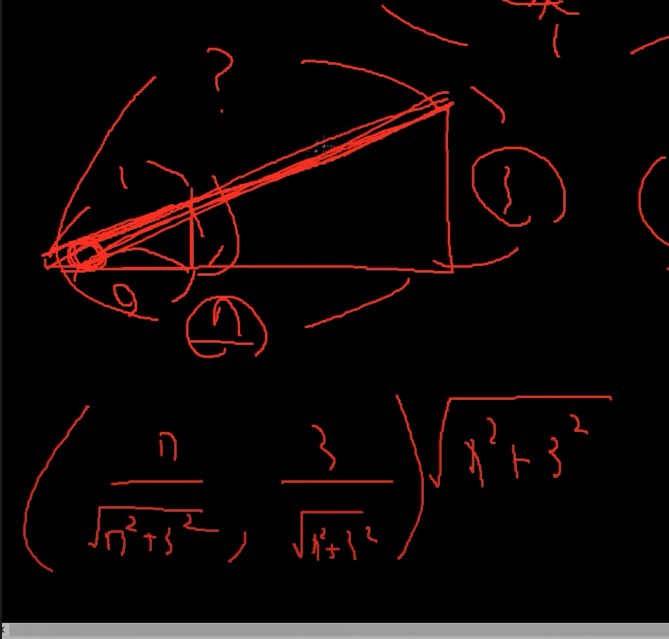
( 7 / √(7^2 + 3^2), 3 / √(7^2 + 3^2) )

이게 정규화 했을 때의 x, y 좌표이다.

이게 길이 1짜리 벡터로 줄였을 때의 좌표이다.

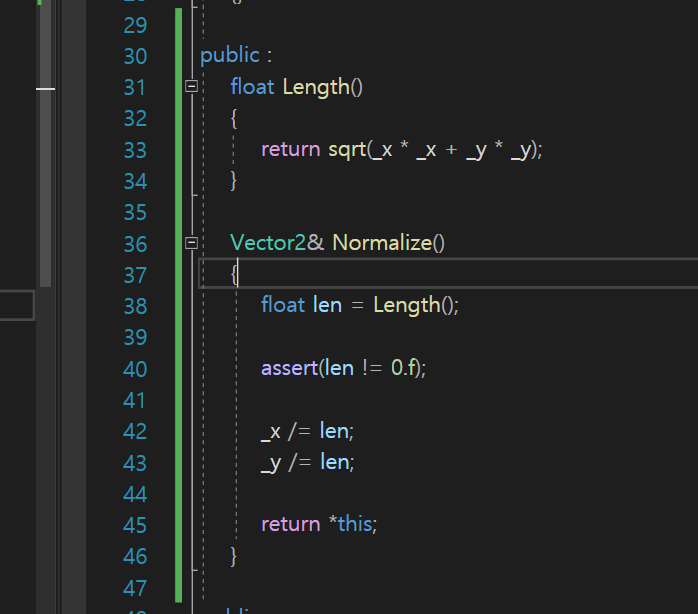
이렇게 Vector 구조체에 함수를 만들어주고 정규화 하는 함수를 하나 만들어준다.

이제부터는 어떻게 하냐하면은

미사일이

이런 각도를 구해서 날아 갈게 아니라.

사용하기 편한이유

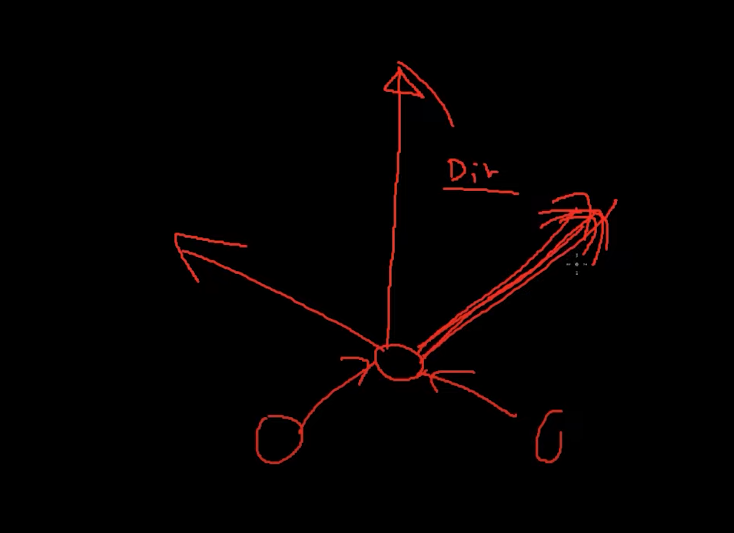
45도 방향으로 갈려는데 오른쪽에서 누군가가 나를 밀고

왼쪽에서도 민다면 나의 최종방향은 위로 가게된다.

근데이게 각도 성분으로 구하게 되면은 굉장히 까다로운데

벡터성분으로 구하게 되면은 간단하게 구해진다.

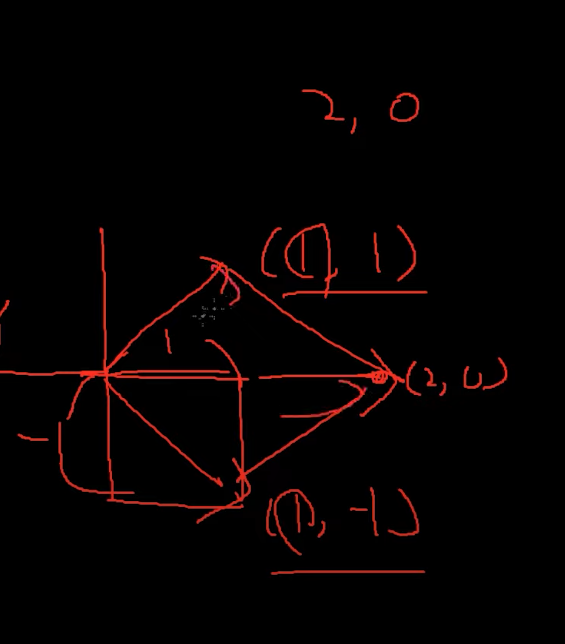
벡터 성분끼리 더해주면 (2, 0) 나온다.

그리고 벡터를 정규화 해놓아야 하는 이유가 '항등원'이기 때문이다.