간단하지만 선형 이진 분류 문제에 더 강력한 알고리즘인 로지스틱 회귀(logistic regression)에 대해 살펴보자.
로지스틱 회귀는 퍼셉트론이나 아달린과 마찬가지로 이진 분류를 위한 선형 모델이다. 아달린의 구조와 굉장히 비슷하게 보이지만 활성화 함수가 시그모이드라는 차이점이 있다. 로지스틱 회귀는 영국의 통계학자인 데이비드 콕스가 1958년 제안한 모델로서 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법이며, 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘이다.
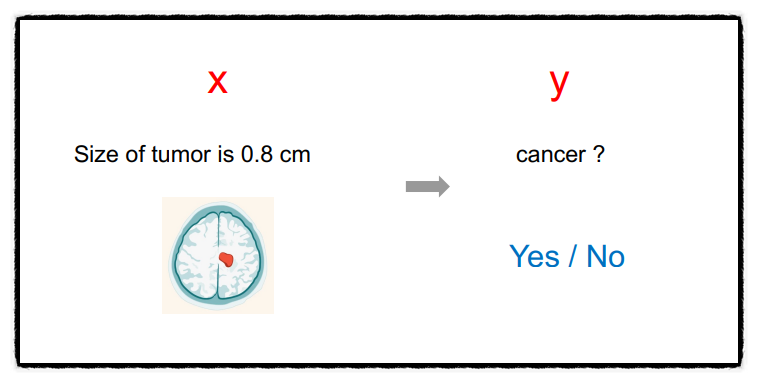위 사진과 같은 예시를 생각하면 쉽다. 예를 들어 종양이 생겼을 때 크기가 0.5cm 이상이면 암에 걸렸다고 분류하고, 0.5cm보다 작은 경우는 암에 걸리지 않았다라고 분류하는 것이다. 이렇게 데이터가 2개의 범주 중 하나에 속하도록 결정하는 것을 이진 분류(binary classification)라고 한다.
로지스틱 회귀 모델에 대해 설명하고 이해하기 위해선 먼저 오즈비(odds raito)에 대해 알아야 한다. 오즈는 특정 이벤트가 발생할 확률이다. 오즈비는 P / (1-P)처럼 쓸 수 있다. 여기서 P는 양성 샘플인 확률이며, 양성 샘플은 좋은 것이라는 의미가 아니며 예측하려는 대상을 뜻한다. 예를 들어 환자가 어떤 질병을 가지고 있을 확률이다.
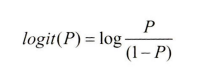오즈비에 로그함수를 취해 로짓(logit) 함수를 정의할 수 있다. 여기서 log는 자연로그로 로짓 함수는 0과 1 사이의 입력값을 받아 실수 범위 값으로 반환한다. 특성의 가중치 합과 로그 오즈 사이의 선형 관계를 다음과 같이 쓸 수 있다.
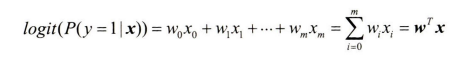여기서 P( y=1 | x )는 특성 x가 주어졌을 때 이 샘플이 클래스 1에 속할 조건부 확률이다. 어떤 샘플이 특정 클래스에 속할 확률을 예측하는 것이 관심 대상이므로 로짓 함수를 거꾸로 뒤집는다. 이 함수를 로지스틱 시그모이드 함수라고 하며, 함수 모양이 S자 형태를 띠고 있기 떄문에 간단하게 줄여서 시그모이드 함수(sigmoid function)라고 한다.
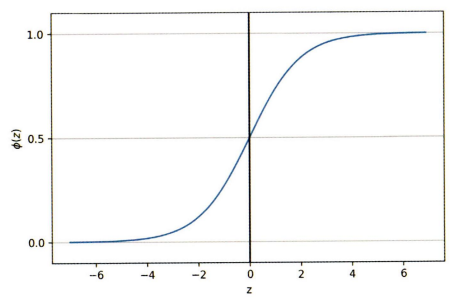z가 무한대로 가면 ∅(z)는 1로 수렴하거나 0으로 수렴하게 되므로 이 시그모이드 함수는 실수 입력 값을 [0, 1] 사이의 값으로 변환한다.
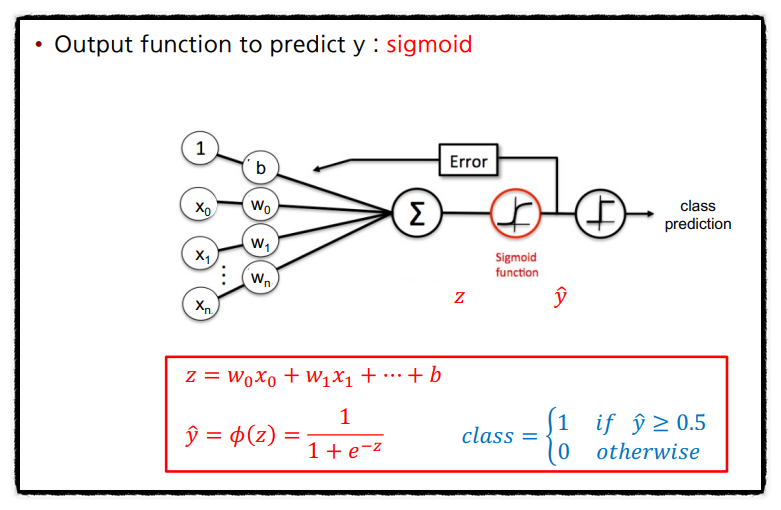가중치 w와 곱해지는 특성 x에 대한 시그모이드 함수의 출력을 특정 샘플이 클래스 1에 속할 확률 ∅(z)=P( y=1 | x; w)로 해석한다. 예를 들어 붓꽃 샘플이 ∅(z) = 0.8이라면 이 샘플은 Iris-versicolor일 확률이 80%라는 뜻이다. 그러므로 이 샘플이 Iris-setosa일 확률은 0.2로 20%가 된다. 예측 확률은 임계 함수를 사용하여 간단하게 이진 출력으로 바꿀 수 있으며 위 시그모이드 함수 그래프와 동일하다는 것을 알 수 있다.
