회귀(Regression)는 주어진 입력 변수(X)와 출력 변수(y) 사이의 관계를 모델링하는데 사용되는 통계적 기법이다. 회귀 분석은 주어진 데이터를 기반으로 예측모델을 만들어 향후 값을 예측하거나 변수 간의 상관 관계를 이해하는데 사용된다.
예를 들어, 크기를 기준으로 주택 가격을 예측하려는 경우 회귀 분석을 사용할 수 있다. 이때 우리는 집의 크기와 가격에 대한 데이터를 수집할 것이며, 두 변수 간의 관계를 파악할 수 있다. 그 후 만들어진 모델을 통해 크기를 주택의 크기를 기준으로 주택의 가격을 예측하는데 사용할 수 있다.
선형 회귀(Linear Regression)
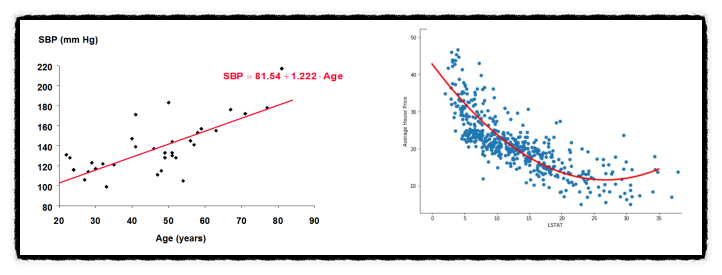선형 회귀(Linear Regression)는 회귀 분석의 일종으로, 입력 변수와 출력 변수 사이의 선형 관계를 모델링하는 기법이다. 선형 회귀는 가장 간단하면서도 널리 사용되는 회귀 알고리즘 중 하나이다.
선형 회귀에서는 입력 변수(독립 변수)와 출력 변수(종속 변수) 사이의 선형 관계를 모델링하기 위해 최적의 직선을 찾는다. 이 직선은 주어진 입력 변수에 대해 출력 변수의 예측값을 계산하기 위해 사용된다.
선형 회귀 모델은 기울기(coefficient)와 절편(intercept)으로 정의된다. 기울기(coefficient)는 입력 변수의 변화에 따른 출력 변수의 변화를 나타내며, 절편(intercept)은 입력 변수가 0일 때의 출력 변수 값을 나타낸다. 선형 회귀 모델은 주어진 데이터에 가장 잘 적합하는 최적의 기울기와 절편을 찾기 위해 학습 알고리즘을 사용하여 모델을 훈련시킨다.
선형 회귀 모델에서 가장 최선의 선을 긋는 방법(모델 파라미터 추정)에는 Gradient descent가 있으며 이를 알아보기 전에 Cost Function(=Loss function; 손실함수)에 대해 알아야 한다.
Cost Function(=Loss function; 손실함수)
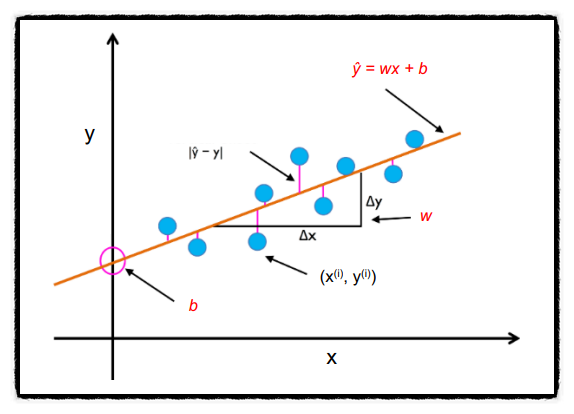위 그래프에서 주황색 선이 예측한 값을 나타내며, 파란색 점은 실제값, 분홍색 선은 오차를 나타내는데, 이 격차가 좁을수록 정확도가 높다. 격차가 음의 값인지, 양의 값인지는 중요하지 않으며 절대값이 중요하다. 예측한 값과 실제값 사이의 거리를 측정하는 것이 Cost Function(=Loss function; 손실함수)이다.
선형회귀의 목적은 가장 작은 값을 가지는 w와 b를 구하는 것이다. 그렇기에 Cost(Loss)를 0에 가깝게 낮춰주는 것이 최종 목적이다.
Gradient Descent(경사 하강법)
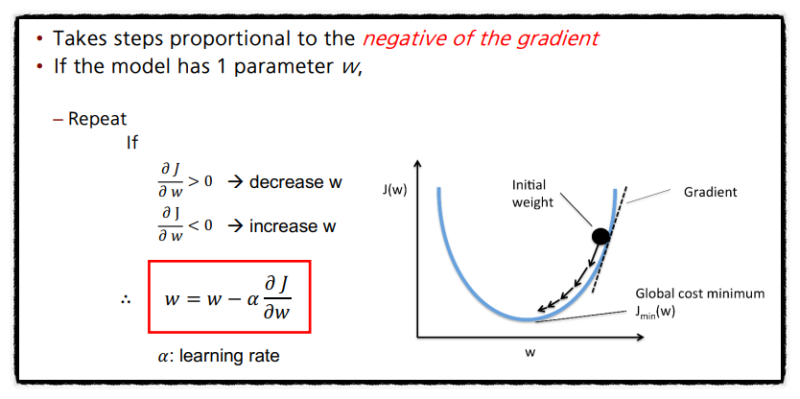
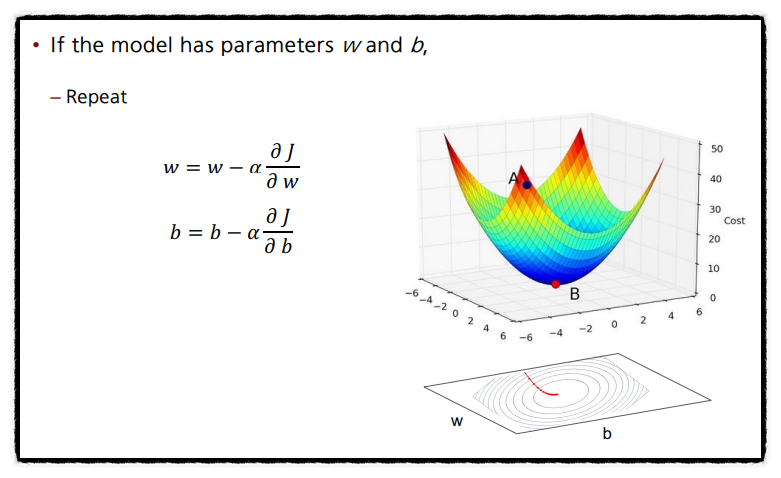
경사하강법은은 손실함수를 최소화하기 위해 모델의 파라미터를 조정하는 방법이다. 경사 하강법은 손실 함수의 기울기(gradient)를 계산하고, 기울기의 반대 방향으로 파라미터를 조금씩 조정하여 손실을 최소화하는 파라미터 값을 찾는다. 이 과정을 손실 함수의 값이 수렴하거나 미리 정의한 반복 횟수에 도달할 때까지 반복한다. 경사 하강법은 주어진 데이터에 대해 손실 함수를 최소화하고, 따라서 선형 회귀 모델의 파라미터를 최적화하는 데 사용된다.
Gradient Descent(경사 하강법) 코드 구현
# Performs gradient descent to fit w, b
def gradient_descent(X, y, w, b, alpha, num_iters):
"""
X (ndarray (m,n)) : data, m examples with n features
y (ndarray (m,)) : target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
alpha (float) : learning rate
num_iters (int) : number of iterations
"""
# a list to store cost J at each iteration
J_history = []
for i in range(num_iters):
# compute the gradient
dj_dw, dj_db = compute_gradient(X, y, w, b)
# update Parameters
w = w - alpha * dj_dw
b = b - alpha * dj_db
# save cost to J_history list
J_history.append(compute_cost(X, y, w, b))
# print cost every 1000 iteration
if (i % 1000) == 0:
print('Iteration %5d: Cost %0.2e ' % (i, J_history[-1]))
return w, b, J_history 