🔎 이진 탐색(Binary Search): 효율적인 검색 알고리즘
📍 이진 탐색의 개념
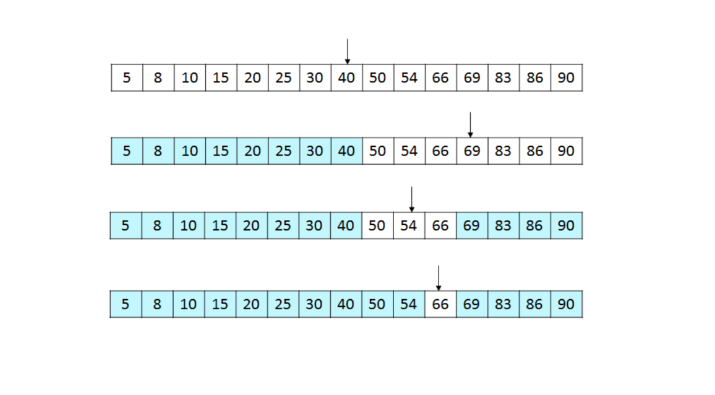
이진 탐색은 정렬된 배열에서 원하는 값을 찾기 위해 배열의 중간 요소와 비교하면서 탐색 범위를 좁혀나가는 방법입니다.
탐색할 값이 중간 요소보다 작으면 왼쪽 반을, 크면 오른쪽 반을 탐색합니다.
이 과정을 반복하면 결국 원하는 값을 찾거나 배열에 값이 없음을 확인할 수 있습니다.
📍 이진 탐색의 동작 과정
초기화:
1. 배열의 시작 인덱스를 left에, 끝 인덱스를 right에 저장합니다.
반복:
1. left가 right보다 작거나 같은 동안 반복합니다.
2. 중간 인덱스 mid를 계산합니다: mid = (left + right) / 2
3. 배열의 중간 요소와 탐색할 값을 비교합니다.
4. 중간 요소가 탐색할 값보다 크면 right를 mid - 1로 설정합니다.
5. 중간 요소가 탐색할 값보다 작으면 left를 mid + 1로 설정합니다.
6. 중간 요소가 탐색할 값과 같으면 값을 찾았으므로 해당 인덱스를 반환합니다.
결과:
1. 반복이 종료될 때까지 값을 찾지 못하면 값이 배열에 없는 것이므로 실패를 반환합니다.
📍 이진 탐색의 구현 예제
다음은 자바를 이용한 이진 탐색의 구현 예제입니다:
public class BinarySearch {
public int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid; // 값을 찾은 경우
} else if (arr[mid] < target) {
left = mid + 1; // 오른쪽 절반 탐색
} else {
right = mid - 1; // 왼쪽 절반 탐색
}
}
return -1; // 값을 찾지 못한 경우
}
public static void main(String[] args) {
BinarySearch bs = new BinarySearch();
int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int target = 5;
int result = bs.binarySearch(arr, target);
if (result != -1) {
System.out.println("Element found at index: " + result);
} else {
System.out.println("Element not found in the array");
}
}
}시간 복잡도
- 이진 탐색의 시간 복잡도는 O(log n)입니다. 이는 탐색 범위를 절반으로 줄이기 때문에 발생하는 특성입니다. 예를 들어, 1000개의 요소가 있는 배열에서 이진 탐색을 사용할 경우, 최대 10번의 비교로 원하는 값을 찾을 수 있습니다. 이는 선형 탐색의 O(n) 시간 복잡도와 비교했을 때 매우 효율적입니다.
활용 사례
- 데이터베이스 검색: 대량의 데이터가 정렬된 상태로 저장되어 있을 때, 이진 탐색을 통해 빠르게 데이터를 검색할 수 있습니다.
- 프로그래밍 문제 해결: 코딩 테스트나 알고리즘 문제에서 효율적인 탐색 방법이 필요할 때 자주 사용됩니다.
- 표준 라이브러리 활용: 많은 프로그래밍 언어의 표준 라이브러리에서 이진 탐색을 지원하는 메서드를 제공합니다. 예를 들어, 자바의 Arrays.binarySearch() 메서드를 활용할 수 있습니다.
이러한 이진탐색을 활용하여 프로그래머스의 예제에 접근해보았습니다.
간단한 문제는 기본적인 이진탐색 코드를 구현하면 되지만,
난이도가 올라갈수록 어떤 것을 이진탐색의 대상으로 볼지 판단하는 게 문제의 key라고 생각했습니다.
프로그래머스의 '순위 검색', '입국심사', '징검다리' 문제를 보며 이진탐색이 필요한 부분을 찾아보겠습니다.
(문제 원문은 생략하고 링크로 대체하겠습니다)
<순위 검색>
이 문제는 개발팀에서 궁금해하는 문의조건에 해당하는 후보자가 몇명인지를 알아내야 합니다.
이 문제 풀이는 2가지 갈래로 생각해볼 수 있습니다.
1. 이진탐색이 필요하지 않은 경우 : 점수를 제외한 항목
2. 이진탐색이 필요한 경우 : 점수 (ex. 100점 이상을 찾아내야함)
1번의 경우 지원자들의 정보에 "-" 라는 경우의 수를 만들어 저장하고, 이를 비교할 것입니다.
2번의 경우 1번 조건을 만족하는 정보중에서 점수를 기준으로 이진탐색합니다. 이를 통해 후보자 수를 알아냅니다.
여러 가지 조건이 비교할 때 조건 자체에 어떤 차이가 있는지 파악하고,
조건에 맞는 탐색이 중요한 문제였습니다.
- 제출 코드
import java.util.*;
class Solution {
public HashMap<String, List<Integer>> map;
public int[] solution(String[] info, String[] query) {
int[] answer = new int[query.length];
map = new HashMap<>();
// 지원자 정보 - 경우의 수 저장
for(int i=0; i<info.length; i++) {
String[] parts = info[i].split(" ");
String[] conditions = {parts[0], parts[1], parts[2], parts[3]};
int score = Integer.parseInt(parts[4]);
makeInfo(conditions, score, 0, "");
}
// 모든 리스트 정렬 (한 번만 수행)
for (String key : map.keySet()) {
Collections.sort(map.get(key));
}
// 요구사항과 일치하는 지원자 정보 저장
for(int i=0; i<query.length; i++) {
String[] parts = query[i].replaceAll(" and ", "").split(" ");
String request = parts[0]; // 요구사항
int score = Integer.parseInt(parts[1]); // 요구점수
int cnt = 0; // 후보자수
// 지원자 맵에 요청사항과 일치하는 key가 있는 경우
if(map.containsKey(request)) {
cnt = countInfo(request, score); // 후보자 수를 리턴
}
answer[i] = cnt;
}
return answer;
}
// 지원자 정보를 경우의 수대로 저장
public void makeInfo(String[] conditions, int score, int depth, String str) {
if(depth == 4) {
if(!map.containsKey(str)) {
map.put(str, new ArrayList<>()); // map에 key 등록
}
map.get(str).add(score); // list에 점수 추가
return;
}
makeInfo(conditions, score, depth+1, str+conditions[depth]);
makeInfo(conditions, score, depth+1, str+"-");
}
public int countInfo(String request, int score) {
List<Integer> list = map.get(request);
// Collections.sort(list);
int left = 0;
int right = list.size();
while(left<right) {
int mid = (left + right) / 2;
int midScore = list.get(mid);
if(score <= midScore) {
right = mid;
} else {
left = mid + 1;
}
}
return list.size() - left;
}
}<입국심사>
이 문제는 입국심사를 마칠 수 있는 가장 최소한의 시간을 찾는 것이었습니다.
이런 경우 시간초를 움직여가면서 몇명이 입국심사를 완료했는지 확인하는 게 핵심이었습니다.
이는 이진탐색으로 접근이 가능합니다.
- 제출 코드
import java.util.*;
class Solution {
public long solution(int n, int[] times) {
long answer = 0;
Arrays.sort(times);
long left = 0;
long right = n * times[times.length - 1]; // 가장 최대치
// left < right 조건
while(left <= right) {
long mid = (left + right) / 2; // 중간 초
long count = 0; // 심사 가능한 사람 수
// 반복문으로 심사 가능한 사람 수 계산
for(int i=0; i<times.length; i++) {
count += mid / times[i];
}
// 필요 인원 초과시
if(count >= n) {
answer = mid;
right = mid - 1;
// 필요인원 이하인 경우
} else {
left = mid + 1;
}
}
return answer;
}
}<징검다리>
이 문제는 개인적으로 참 어려웠는데요. 돌을 랜덤으로 부술 수 있는데 어떻게 중간 지점을 잡아 이진탐색을 할지가 고민이었습니다.
문제에서 요구하는 바는 돌을 랜덤으로 부수면서 각 지점 사이의 최솟값 중 최댓값을 찾는 것이었습니다.
즉, 최솟값의 범위를 이진탐색으로 움직여 가면서 최솟값 중의 최댓값을 알아내는 문제였습니다.
최솟값을 움직여서 어떻게 답을 알 수 있느냐?
최솟값 보다 작은 거리를 가지는 돌들을 부수면 됩니다. -> 그 어떤 돌도 최솟값보다 작은 거리는 가지지 않을 것입니다.
그리고 이 부순 갯수를 세서 인자로 들어온 n과 비교해가며 이분탐색으로 최솟값 중 최댓값에 도달하면 됩니다.
- 제출 코드
import java.util.*;
class Solution {
public int solution(int distance, int[] rocks, int n) {
int answer = 0;
Arrays.sort(rocks);
int left = 0;
int right = distance;
while(left <= right) {
int mid = (left + right) / 2;
int bronkenRocks = getBrokenRocks(distance, rocks, mid);
if(bronkenRocks <= n) {
left = mid + 1;
answer = mid;
} else {
right = mid - 1;
}
}
return answer;
}
public int getBrokenRocks(int distance, int[] rocks, int mid) {
int cnt = 0;
int prev = 0;
for(int i=0; i<rocks.length; i++) {
if(rocks[i] - prev < mid) {
cnt++;
} else {
prev = rocks[i];
}
}
if(distance - prev < mid) cnt++;
return cnt;
}
}이진탐색은 시간복잡도가 낮은 매우 효율적인 알고리즘으로, 무엇을 이진탐색으로 기준으로 삼을 것인가에 따라 활용도가 좋을 것 같습니다.
저는 위의 예제들을 풀면서 이진탐색의 기준을 유연하게 사고해야겠다는 생각이 들었습니다.
피드백은 언제든 환영입니다. 감사합니다 :)
