차원 축소 알고리즘을 비교해보자 (PCA, T-sne, UMAP)
차원 축소 알고리즘
- 차원 축소 알고리즘들은 축소하는 방법에 의해 두 가지로 나눌 수 있음
- matrix factorization 계열 - pca
- neighbour graphs - t-sne, umap
PCA
- matrix factorization 을 base 로 함 (공분산 행렬에 대해서 svd 등)
- 분산이 최대인 축을 찾고, 이 축과 직교이면서 분산이 최대인 두번째 축을 찾아 투영시키는 방식(공분산 행렬의 고유값과 고유벡터를 구하여 산출)
- 단점 : 선형 방식으로 정사영하면서 차원의 축소 -> 군집된 데이터들이 뭉게지는 단점
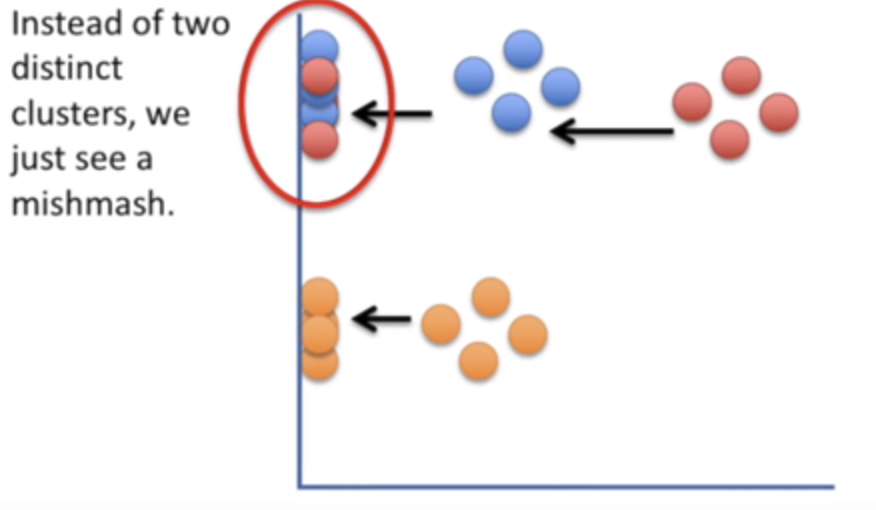
t-sne
- neighboring graph 를 base 로 함
- Local neighbor structure를 보존(고차원의 벡터의 유사성이 저차원에서도 유사도록 보존)
- t 분포를 이용해 하나의 기준점을 정하고 모든 다른 데이터와 거리를 구한 후 그 값에 해당하는 t 분포 값을 선택, 값이 유사한 데이터끼리 묶어줌
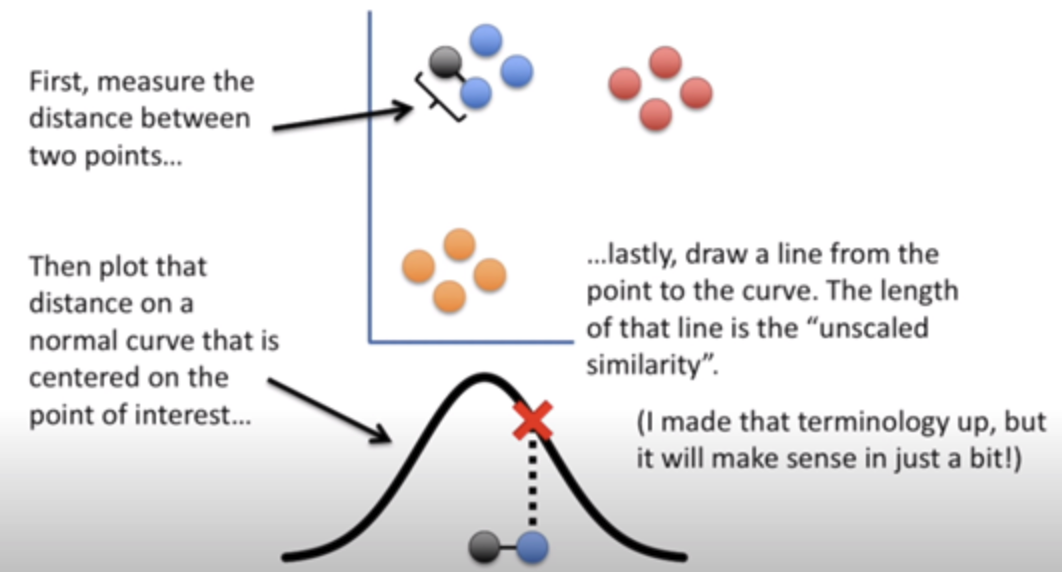
- 단점
- 데이터의 개수가 n개라면 연산량은 n의 제곱만큼 늘어남
- 매번 돌릴 때마다 다른 시각화 결과가 나옴(training 과 prediction 을 동시에... -> 학습에 활용할 수 없게 됨)
- 오로지 2,3차원으로만 줄일 수 있음
UMAP
- (uniform manifold approximation and projection)
- neighboring graph 를 base로 함
- 가장 좋은 성능을 내는 알고리즘이라고 알려짐 (UMAP is arguably the best performing as it keeps a significant portion of the high-dimensional local structure in lower dimensionality (https://towardsdatascience.com/topic-modeling-with-bert-779f7db187e6))
- 방법
- high dimension space 에서의 데이터를 graph로 만들고, low dimension 으로 graph projection한다 (이 전 과정이 유효하다고 수학적으로 증명돼있다고 함)
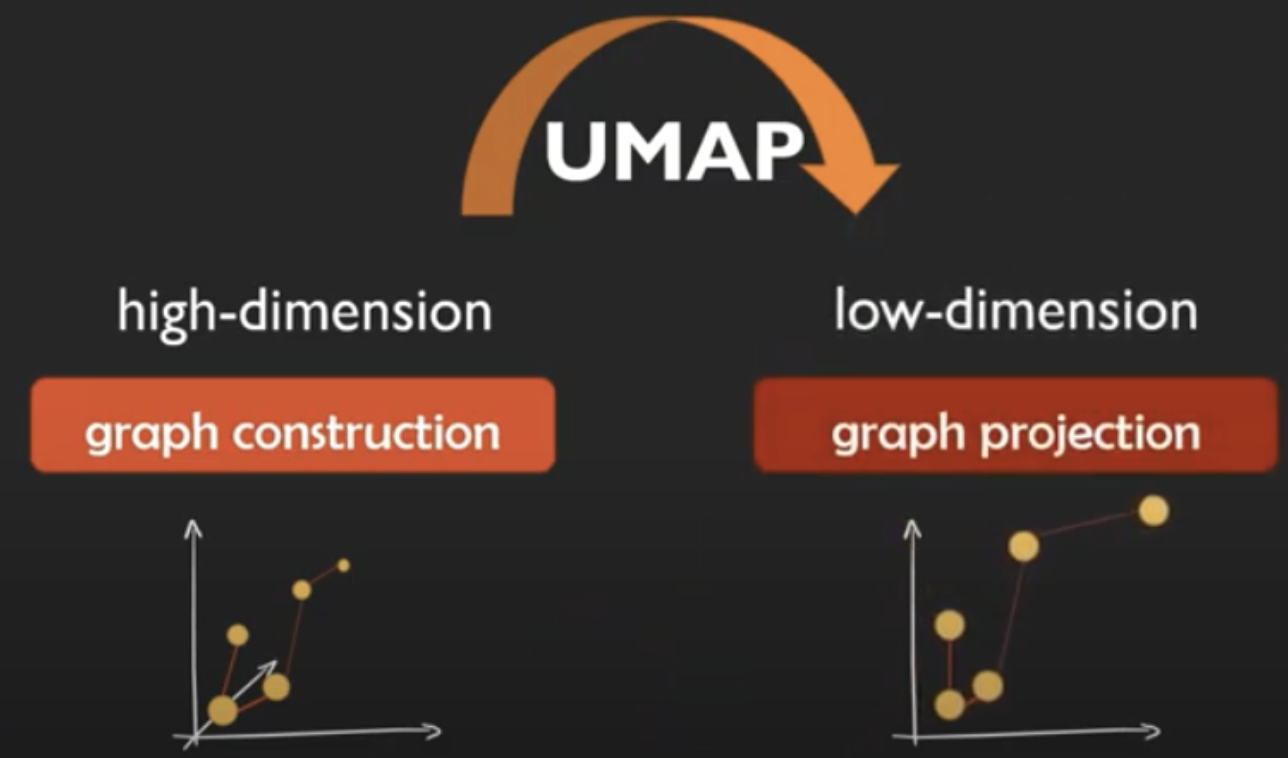
- data point 에서 simplex 복합체로 만들어서 graph 구성한다 (nerve theorem: 이렇게 구성이 가능함을 증명)
- 각 node 에서의 길이 k의 radius 를 그림(knn 등 이용 - 정해진 nearest neighbor n개 만큼을 포함하게 되는 radius k를 그림)
- k가 작으면 local structure, 크면 global structure 를 가져올 수 있음 → 이때 겹치는 정도로 connection 의 weight 를 결정
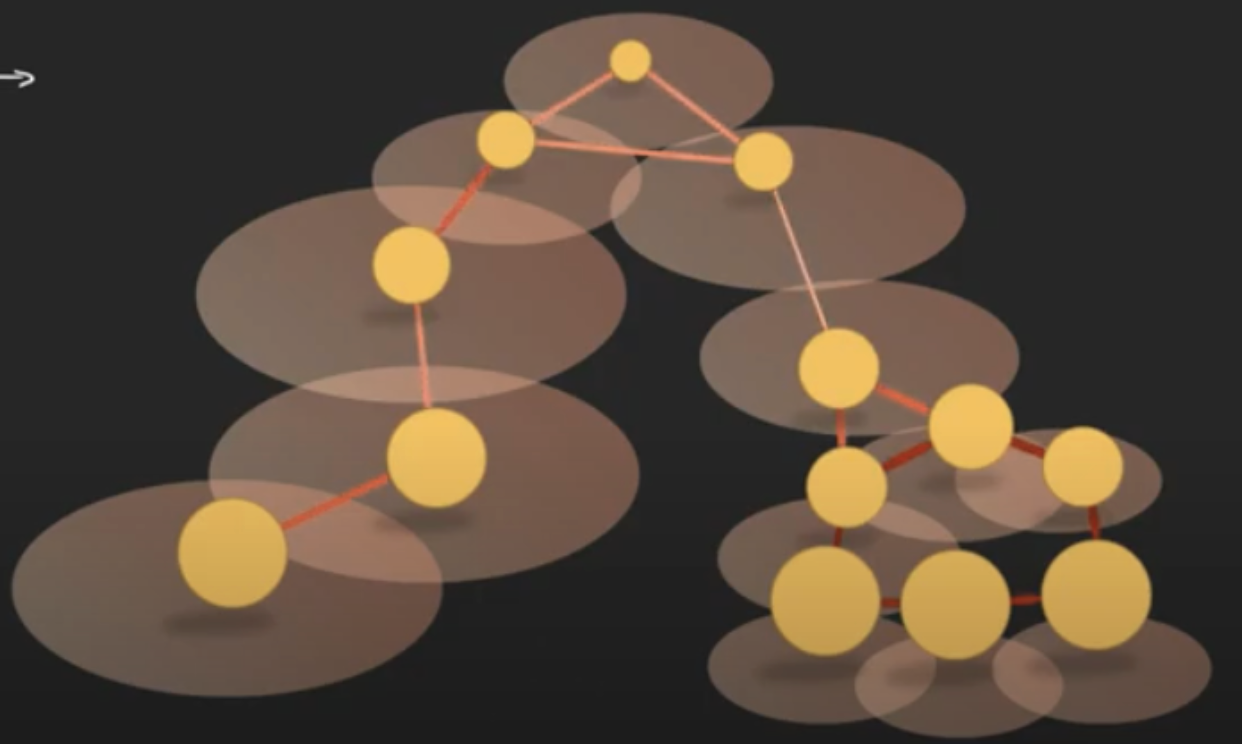
- 이 strength 를 그대로 저차원으로 이동시킨게 umap이다.
- (이 과정에서 퍼지이론, 리만 매니폴드 등등 뭔가 생소한 개념이 많이 들어가는데 어쨋거나 이런저런 방법으로 umap이 완성된다고 한다...)
- 장점
- 빠르다
- embedding 차원 크기에 대한 제한이 없어서 일반적인 차원 축소 알고리즘으로 적용 가능함
- global structure 를 더 잘 보존(시각화도 더 예쁘게 잘 된다)
- 탄탄한 이론적 배경 - 리만 기하학 & 위상수학에 기반함(논문 저자에 의하면 이론적 디테일은 모르는게 정신 건강에 이롭다고 한다 ㅋㅋㅋ)
umap vs pca
- hyper parameter
- umap
- n_neighbors, min_dist 두개의 hyperparameter 존재
- (단 top2vec 이라는 논문에서 최적의 parameter를 제안한 바 있음(n_neighbor =15, min_dist=0.25)
- pca
- structure 보존
- hyper parameter 가 없다는 점에서는 pca 가 유용하지만, 아래 reference 들을 참고해보면 umap 이 훨씬 낫다는 글이 워낙 많아서,,, hyper parameter 조율할 여유가 있으면 umap, 엄청 급하면 pca를 쓰면 될 것 같다.
Reference



