DEEP DOUBLE DESCENT: WHERE BIGGER MODELS AND MORE DATA HURT (2020, ICLR)
Classical vs Modern에서의 직관
- classical한 통계분야에서 '모델이 너무 크면 좋지 않다'라는게 기본적인 인식있음
- (Bias-variance trade-off: 모델 복잡도가 올라가면 bias는 작아지지만, variance 는 커진다)
- 반면 뉴럴넷에서는 '모델은 클수록 좋다'라는 인식이 있다.
- 또한 효율적인 training 시간에 대한 논의도 진행 중
- early stopping이 test performance 를 증가시킨다 vs error 가 0까지 충분히 수렴할때까지 triaining 시키는게 낫다)
- 모델 크기와 트레이닝 시간에 대한 논쟁은 많을지라도, '데이터는 많을수록 좋다' 라는 점에 대해서는 전통적인 분야에서도 neural net 분야에서도 동의하는 부분
Double descent
- deep learning 모델은 모델 복잡도와 training/testing error 와의 관계에서 두 개의 서로 다른 regime(구간)을 가지게 된다.
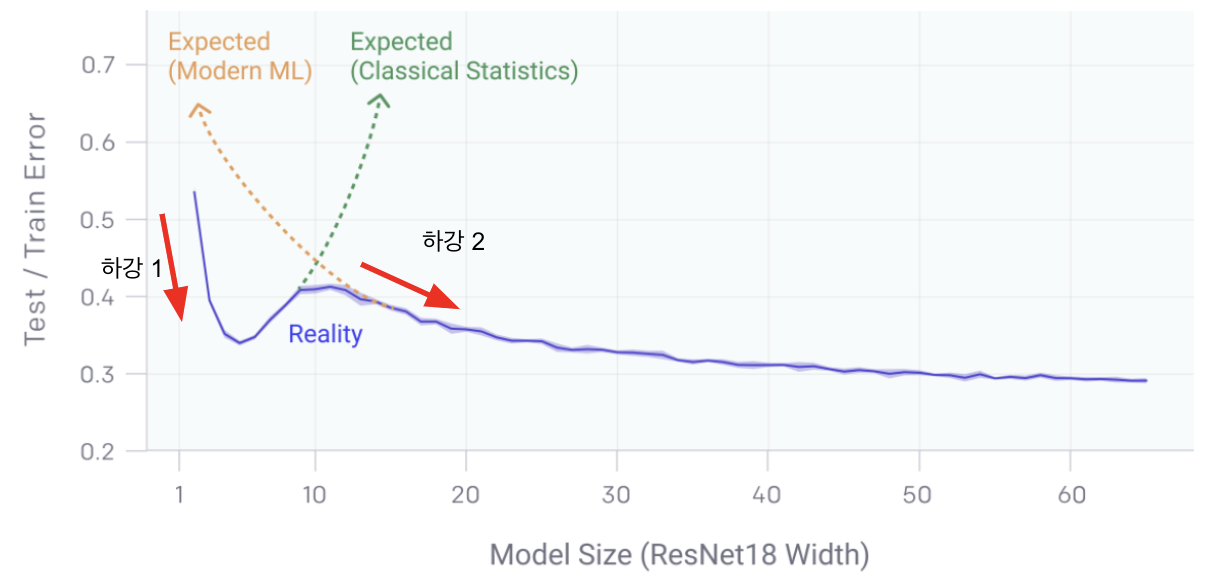
- 구간1. Under-parameterized regime (underfitting 구간)
- 모델이 충분히 복잡하지 않은 구간에서는 복잡해질수록 training/test error 감소
- 요 구간을 쫌 지나면, classical 한 통계분야에서와 마찬가지로 Bias-variance trade-off가 발생함 (모델이 복잡해질수록 오히려 error 가 상승)
- 구간2. Over-parameterized regime(overfitting 이 발생하는 구간)
- 모델이 충분히 커져서 trade-off 구간을 뛰어넘으면, 즉 0에 가까운 training error를 달성하고 나면, 그 이상 복잡도를 증가시켰을때에 "모델은 클수록 좋다"라는 현대적 직관에 따라 테스트 오류만 감소한다.
- 위의 두 개의 구간에서 test/training error 가 한번씩 하강하는 곡선을 그리게 되는데 (구간 1에서 하강하다 상승, 구간 2에서 다시 하강) 이걸 double descent 라고 부른다.
- (근데 double descent 의 발견은 이 논문에서 처음 한 건 아니다. 이미 다른 논문들에서 밝힌 바 있고, 이게 이 논문의 main contribution은 아니다)
Main contribution
- double descent 현상이 다양한 task, architecture, optimization method 에서 일어나는 흔한 현상임을 실험으로 밝혔다.
- (이 논문은 실험만으로 쓰여진 논문이라고 봐도 과언이 아니다, 정말 많은 실험으로써 증명했다...)
- model complexity 뿐 아니라 epoch 에도 double descent 가 영향받음을 보였다.
- 모델이 아주 가볍거나, 아주 무거울때에는 epoch을 증가시킬수록 error 가 감소하지만, 그 중간 사이즈의 모델의 경우에는 오히려 epoch 을 늘릴수록 증가하는 구간이 발생한다.

- 모델이 아주 가볍거나, 아주 무거울때에는 epoch을 증가시킬수록 error 가 감소하지만, 그 중간 사이즈의 모델의 경우에는 오히려 epoch 을 늘릴수록 증가하는 구간이 발생한다.
- 위의 왼쪽 그래프에서 resnet 의 parameter를 증가시킬수록 error 가 감소하다가 어느 순간부터 다시 증가하고 (이 증가에 돌입해서 다시 감소하여 이전보다 error 가 감소하기까지의 구간을 critical regime 이라 부른다) 어떤 임계점을 지나고 나면 다시 감소한다.(이 임계점을 interpolation threshold라 부른다)
- 위의 오른쪽 그래프에서 보면 epoch의 증감에 따라 double descent 양상이 달라짐을 알 수 있다. 모델이 아주 가볍거나, 아주 무거울때에는 epoch을 증가시킬수록 error 가 감소하지만, 그 중간 사이즈의 모델의 경우에는 오히려 epoch 을 늘릴수록 증가하는 구간이 발생한다.
- Effective Model Complexity (EMC)라는 Complexity measurement를 도입하고 double descent 는 EMC 의 function으로 나타낼 수 있음을 보였다.
- EMC : 모델의 training error 를 0에 가깝게 만들어주는 최대 데이터의 갯수 (EMC 가 클수록 complexity 가 높은 것)
- -> 왜 갑자기 데이터 수가 나올까?
- 모델이 복잡할수록 더 많은 데이터로 학습시켜야 training error 가 0으로 갈 수 있다.
- 즉, EMC 가 크다는 것은 complexity 가 높은 것.
실험 결과
가설과 검증

- EMC
- main contribution 부분에서 밝혔듯, 이 논문에서는 EMC 라는 모델의 복잡성을 나타낼 지표를 제안한다.
- 모델의 training error 를 0에 가깝게 만들어주는 최대 training 데이터의 갯수를 뜻하며, EMC 가 클수록 complexity 가 높은 것이다.)
- 위의 EMC 를 바탕으로 각 구간에서 아래와 같이 세가지 가정을 세운다.
- Under-paremeterized regime - Under fit 구간에서 EMC가 충분히 작다면, test error가 작아질 것이다.
- Over-parameterized regime - Over fit 구간에서 EMC가 충분히 크다면, test error 가 작아질 것이다.
- Critically parameterized regime - underfit 구간과 overfit 구간이 교차되는 지점에서는 test error 를 증가시킬수도, 감소시킬수도 있다.
Double Descent 현상의 실험
double decent 는 Model size 와 epoch에 dependent 하다
- 논문에서 진행한 실험을 다 볼 필요는 없을 것 같고, 사실 논문 맨 처음에 나온 사진이 모든 실험을 요약해준다.

- 여러 모델을 실험해봤더니 model size 뿐만이 아니라 train epoch double descent 가 일반적으로 관측되었다고 한다.
- 위의 왼쪽 그래프에서 resnet 의 parameter를 증가시킬수록 error 가 감소하다가 어느 순간부터 다시 증가하고 (이 증가에 돌입해서 다시 감소하여 이전보다 error 가 감소하기까지의 구간을 critical regime 이라 부른다) 어떤 임계점을 지나고 나면 다시 감소한다.(이 임계점을 interpolation threshold라 부른다)
- 위의 오른쪽 그래프에서 보면 epoch의 증감에 따라 double descent 양상이 달라짐을 알 수 있다. 모델이 아주 가볍거나, 아주 무거울때에는 epoch을 증가시킬수록 error 가 감소하지만, 그 중간 사이즈의 모델의 경우에는 오히려 epoch 을 늘릴수록 증가하는 구간이 발생한다.
Model-Wise Double Descent
- 여러 학습 세팅을 바꾼 상태에서, 모델 size 를 키웠을 때, double descent 현상이 어떻게 나타나는지 실험했다.
Label noise 에 따른 Double Descent
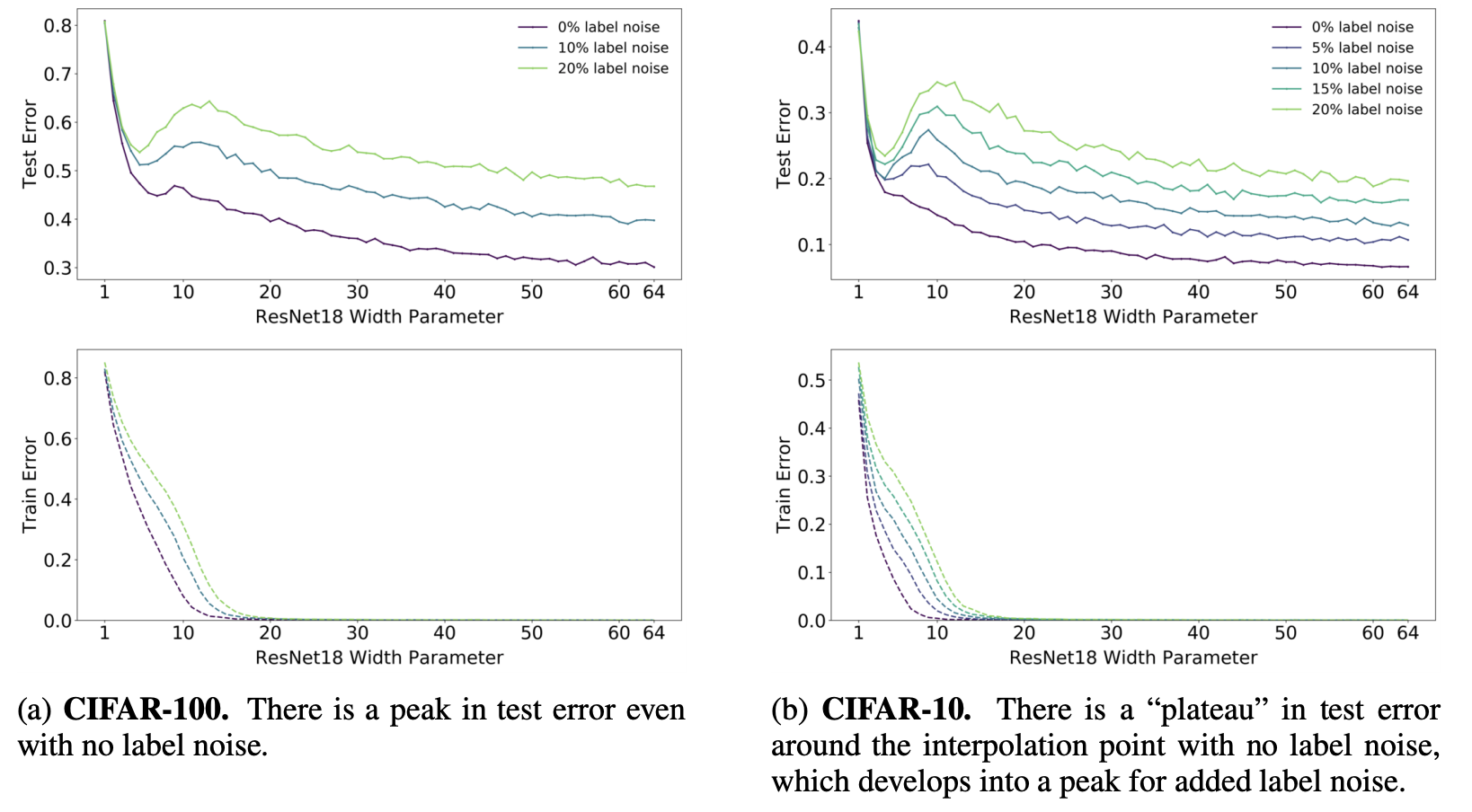
- label noise 가 커질수록 double descent 현상이 심화된다.
Data augmentation 의 효과
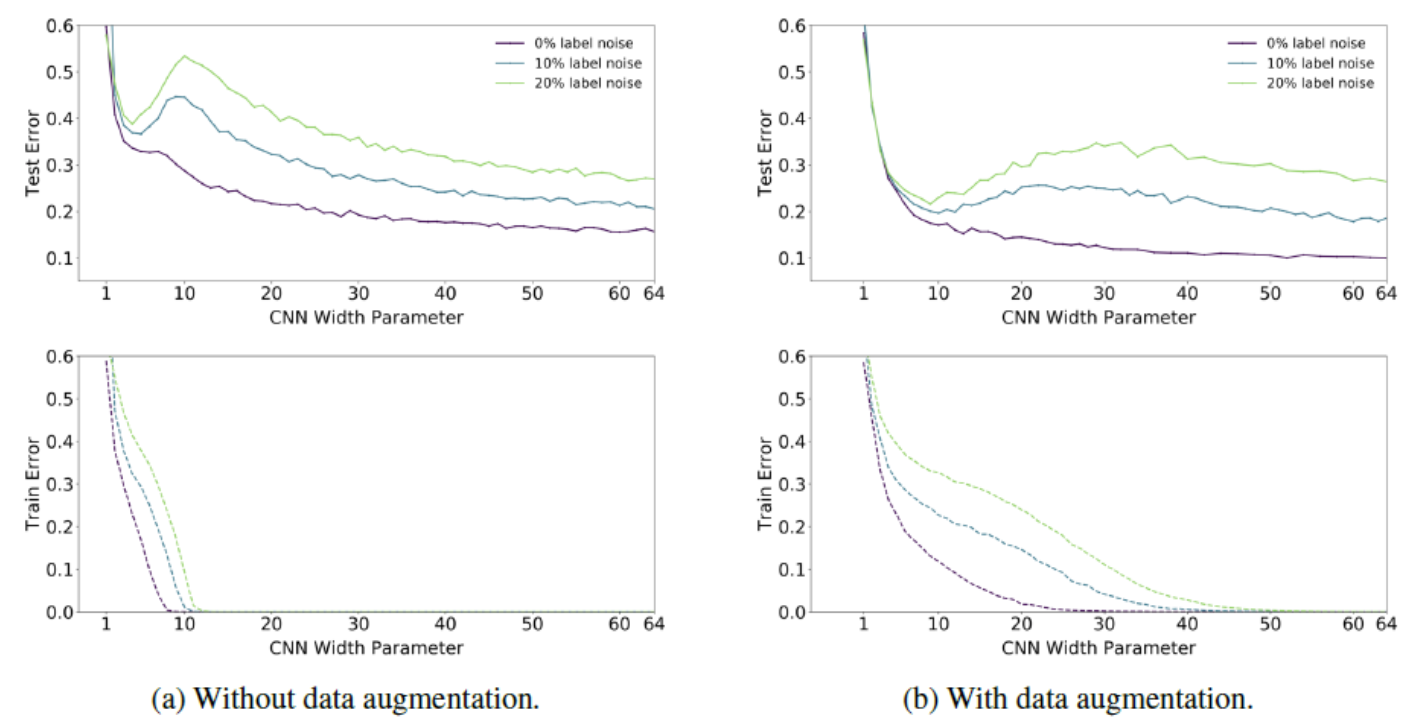
- augmentation 을 하면 double descent 가 완화된다.
Optimizer
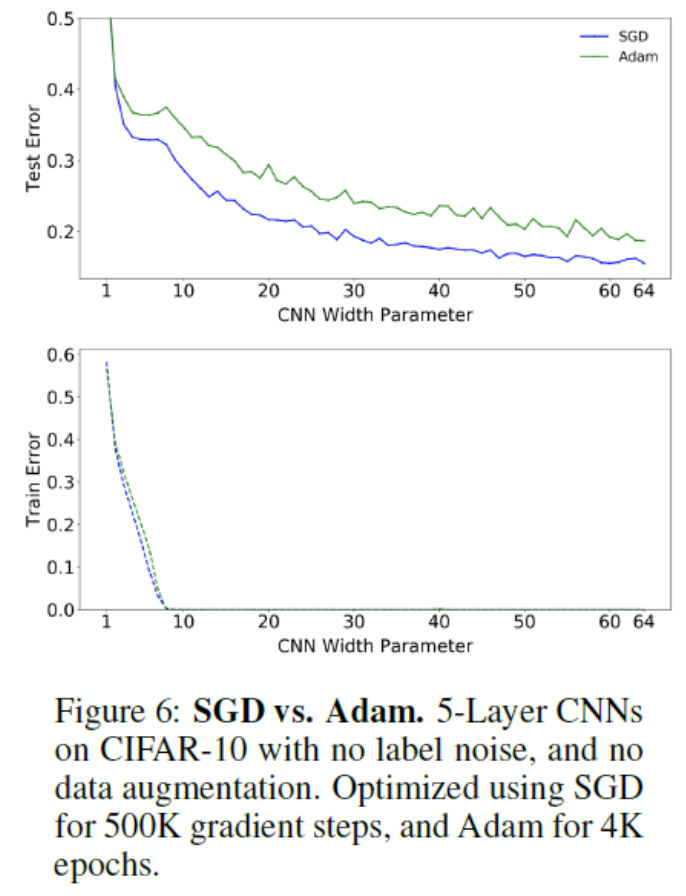
- 어떤 optimizer 를 써도 double descent 는 일어난다.
Embedding dimension
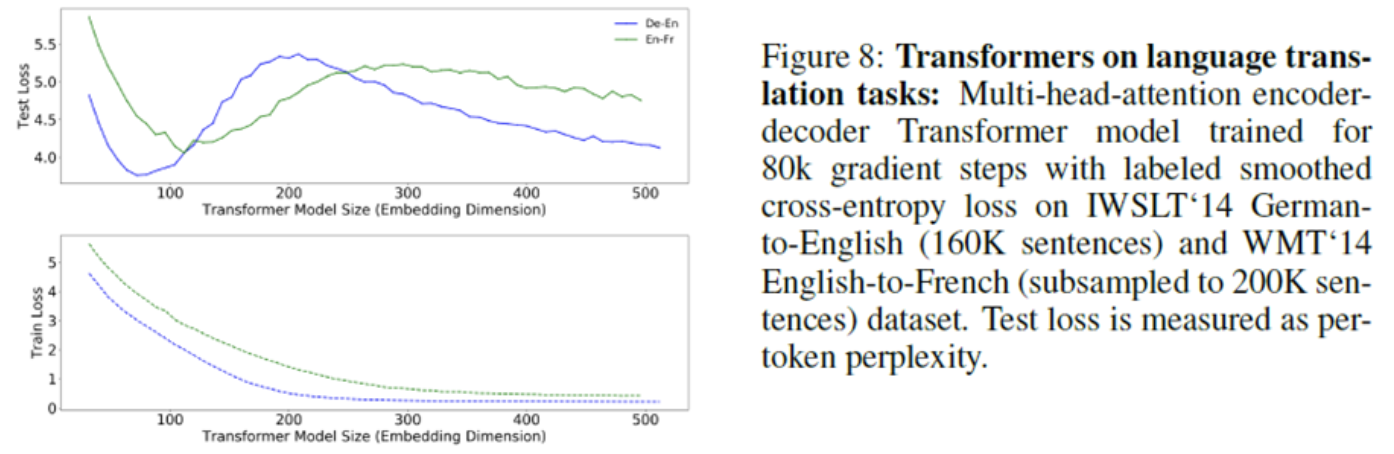
- 일반적으로 embedding size 가 크면 모델 성능이 좋아지지만,