KPMG Future Academy AI 활용 데이터 분석가 3기 44일차 수업을 2025년 1월 20일에 참석했다.
- 머신러닝 추론 통계
1.1. 확률 분석
1.1.1. 회귀 (linear regression)
1.1.2. 분류 (decision tree)
1.2. 알고리즘
1. 머신러닝 추론 통계
1.1. 확률 분석
1.1.1. 회귀
실습
보스톤 집값 예측해보기
데이터 설명
- crim: 자치시(Town)별 1인당 범죄율
- zn: 25,000 평방피트를 초과하는 거주지역 비율
- indus: 비소매상업지역이 점유하고 있는 토지 비율
- chas: 찰스강에 대한 더미 변수 (= 1 강 경계에 위치; 0 나머지)
- nox: 10ppm당 농축 일산화질소
- rm: 주택 1가구당 평균 방 개수
- age: 1940년 이전에 건축된 소유주택 비율
- dis: 5개 보스턴 직업센터까지 접근성 지수
- rad: 방사형 도로까지의 접근성 지수
- tax: 10,000달러 당 재산세율
- ptratio: 자치시(Town)별 학생/교사 비율
- lstat: 모집단 하위 계층의 비율(%)
- medv: 본인 소유 주택가격(중앙값) (단위:$1,000)
상위 값
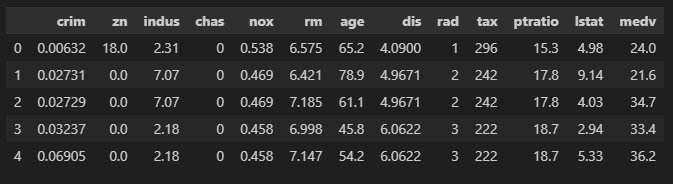
기술 통계
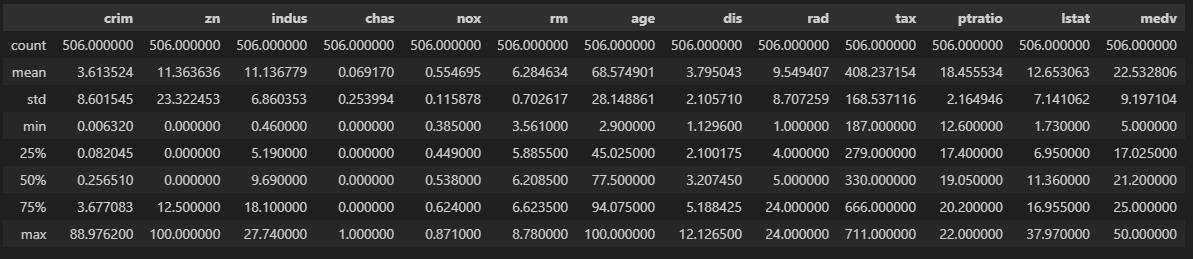
zn의 std(표준편차)가 23.3224와 같이 큰 값으로 나왔다.
데이터는 0이 다수 포함돼있다. (특정 조건을 만족하지 못 하는 경우 0)
해당 변수의 표준편차를 참조할 때는 주의가 필요해보인다.

우선 변수 몇 가지 시각화해봄.
주거 지역 밀집도와 집값 상관관계
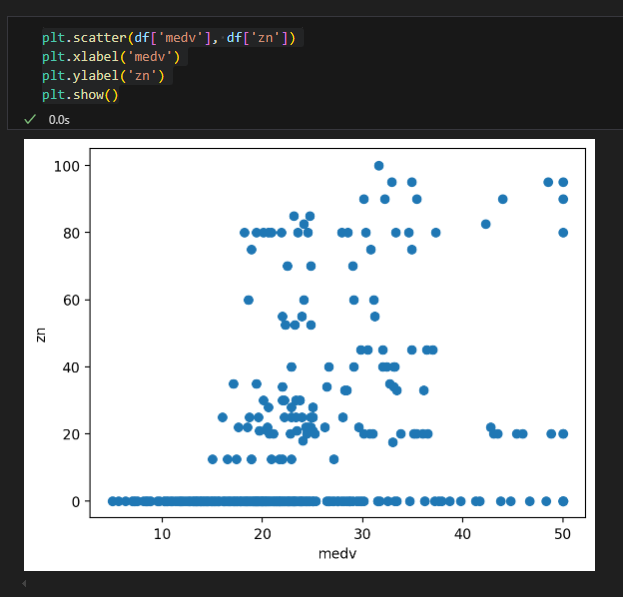
교사 당 학생수와 집값 상관관계
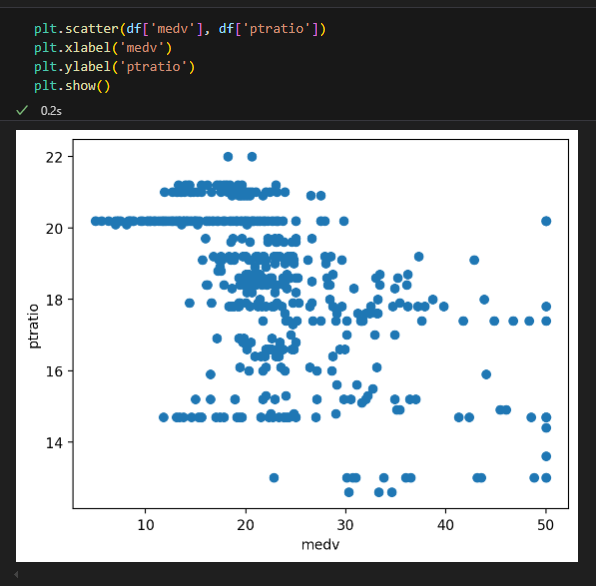

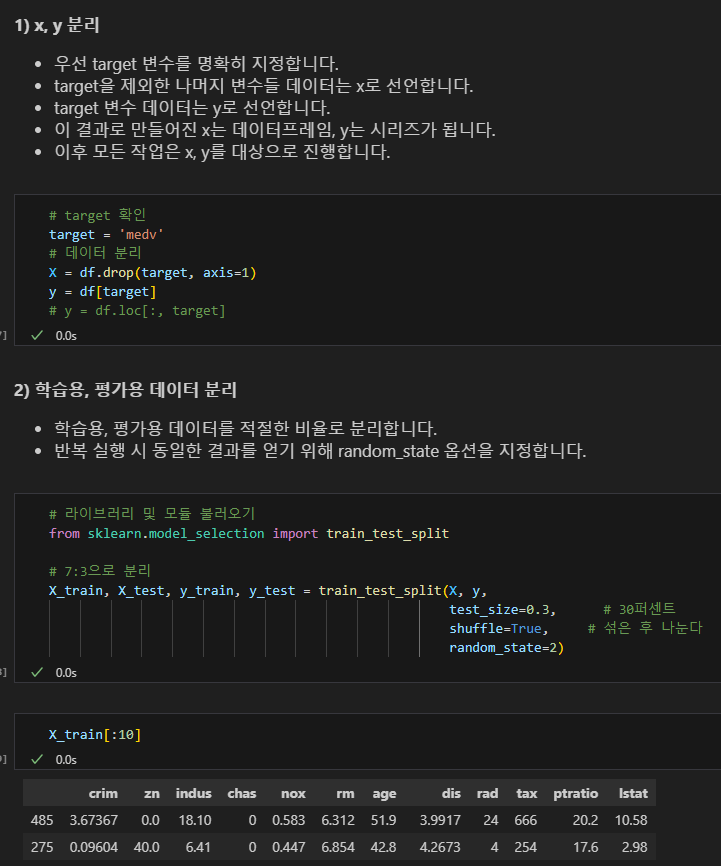
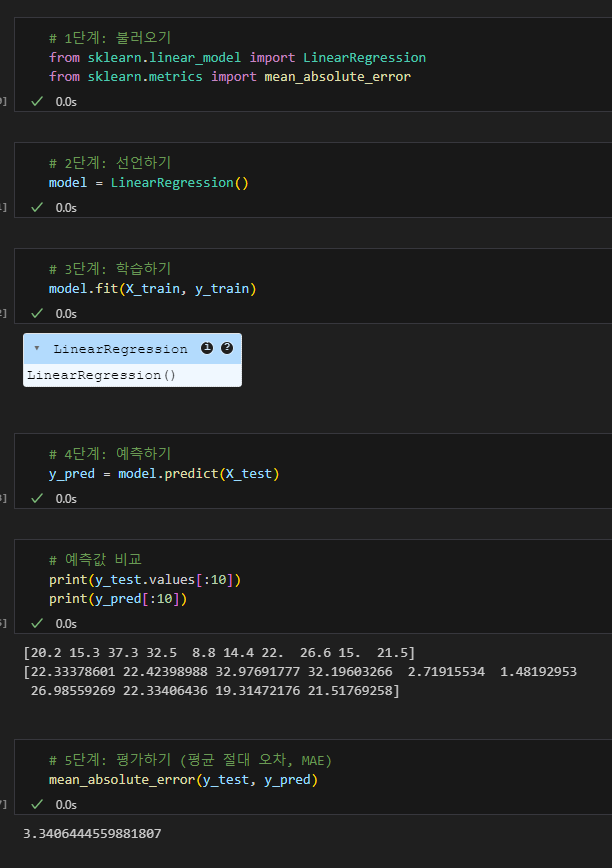
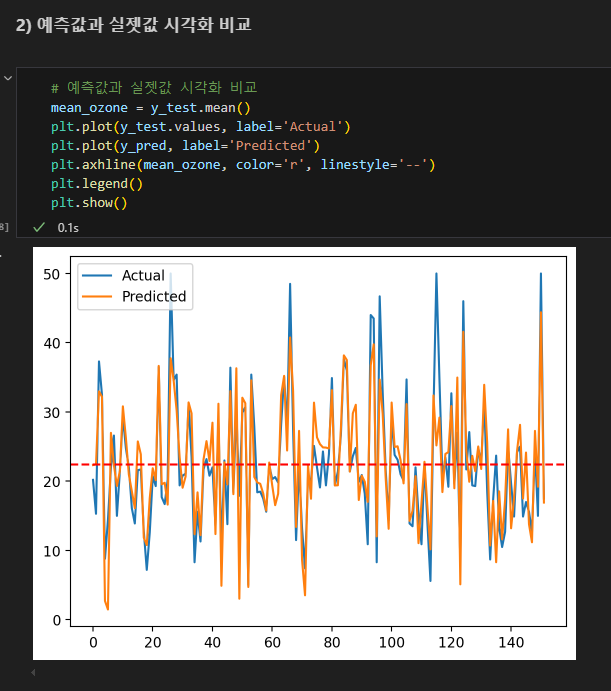
보스톤 집값에 대해 주어진 변수들을 기반으로 높은 예측률을 보임
성능 평가
회귀 모델 평가 : 예측값과 실제값의 차이(=오차)로 모델 성능을 평가
분류 모델 평가 : 정확히 예측한 비율로 모델 성능을 평가
y : 실제값 / y^ : 예측값 / yˉ : 평균값
오차 합 구하기
오차 제곱의 합
오차 절대값의 합
SSE : Sum Squared Error
MSE : Mean SSE
RMSE : Root
MAE : Mean Absolute Error
MAPE : Mean Absolute Percentage Error
위 값이 모두 작을수록 모델 성능이 좋은 것
mean_absolute_error
오차를 바라보는 관점
SST(Sum Squared Total) : 반드시 존재하는 오차. 최소한 평균보다는 좋은 모델이 되어야 함
SSR(Sum Squared Regression) : 회귀 모델이 잡아낸(설명 가능한) 오차량을 의미
SSE(Sum Squared Error) : 전체 오차 중에서 회귀식이 여전히 잡아내지 못한 오차(잔차, Residual Error)
결정계수 R^2
MSE로 설명이 부족한 부분. 성능이 확실히 와닿지 않음.
모델의 적합도를 측정. 얼마나 잘 데이터를 설명하는지 나타냄.
R^2 = SSR/SST
R^2 = 1 이면 MSE = 0으로 성능이 좋다는 뜻
변수 개수가 많아지면 R^2가 자연스럽게 증가함.
다른 지표도 같이 고려해야함
오차 구하기
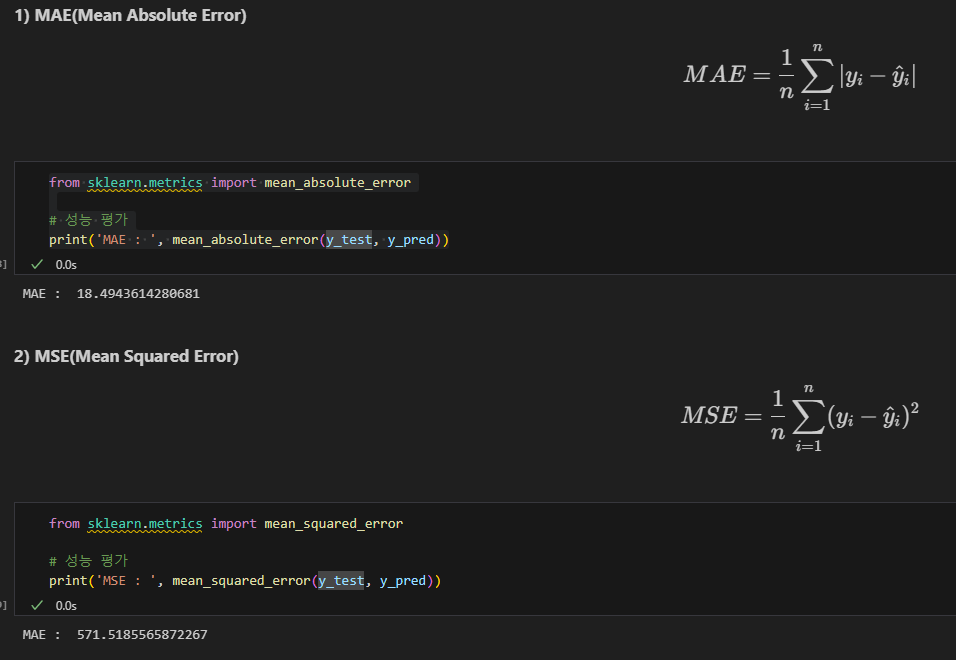
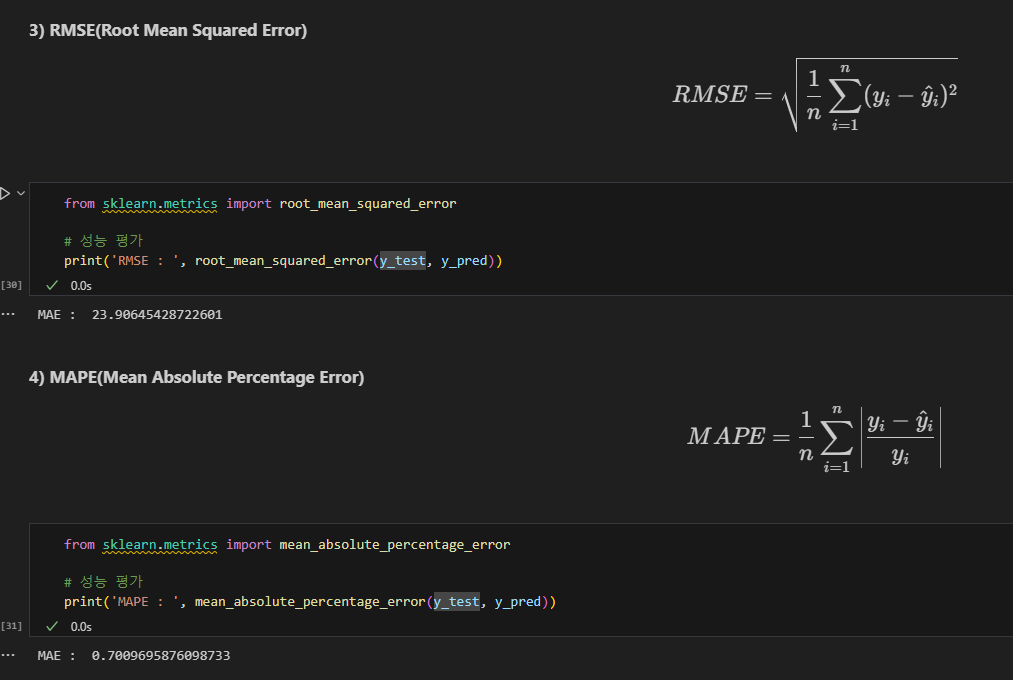
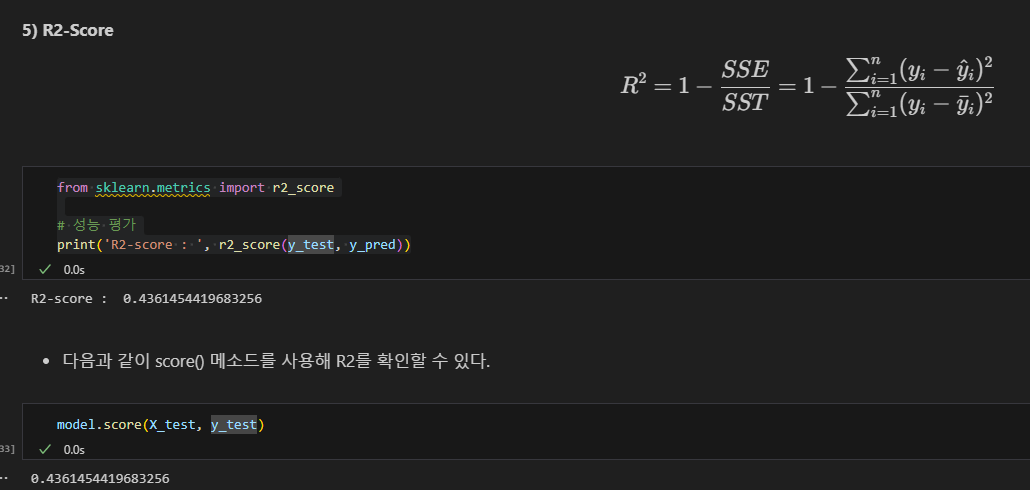
보스톤 집값 예측, 수입과 행복의 상관 예측을 진행해본 결과:
수입과 행복의 상관 예측이 MAE, MAPE 등 오차는 더 낮게 나왔지만 결정계수는 0.75로 보스톤 0.74와 유사하게 나왔다. 즉 모델이 변동을 잘 따라가는지는 결정계수를 확인하면 된다.
1.1.2. 분류
예측 모델의 정확도 함정 : 데이터 불균형의 문제를 고려해야함
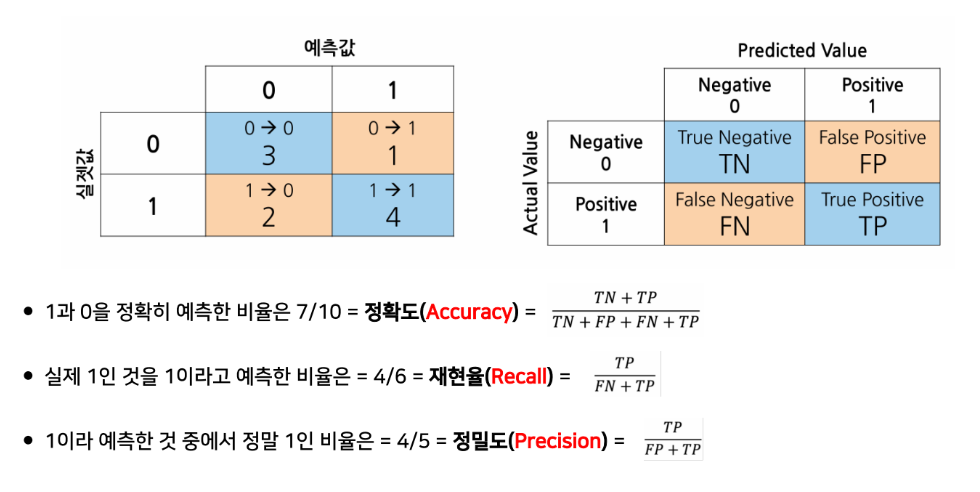
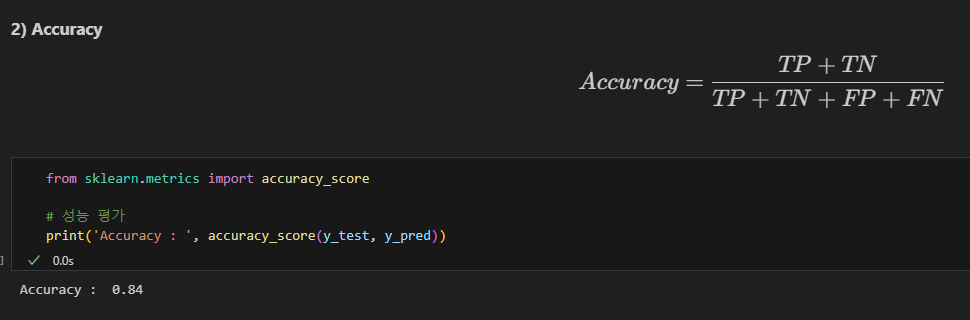
정확도 accuracy : 전체 샘플 중에서 올바르게 예측한 비율
재현율 recall : positive 중에서 positive로 예측한 비율. 민감도
정밀도 precision : positive로 예측한 것 중에서 실제 positive인 비율
정밀도와 재현율은 trade-off 관계로 적정한 비율이 필요함.
특이도 : 실제 negative 중에서 negative로 예측한 비율. (불필요한 조치를 줄일 때 사용)
혼동 행렬
오차 행렬
TN 진음성
FP 위양성
FN 위음성
TP 진양성
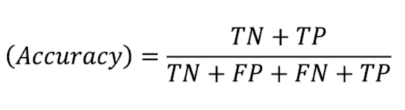
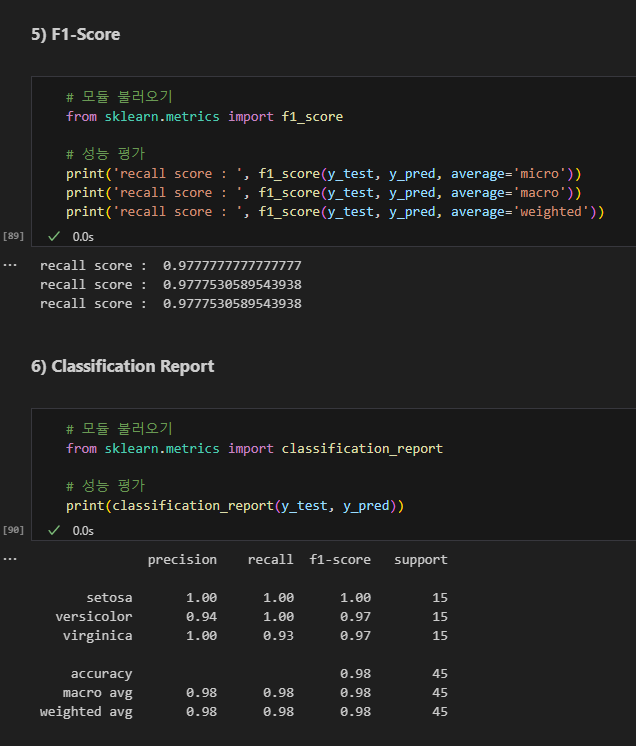
F1-Score
의료 진단, 스팸 이메일 필터링 등에서 중요한 지표로 사용.
양성 예측의 정확성, 모든 양성을 잘 탐지하는 능력의 균형을 중요시하기 때문.
정밀도와 재현율 간의 균형 평균.
KNN 알고리즘 사용해서 입학 결과 예측
x, y 분리, target 지정 등 위의 과정은 동일
confusion matrix로 성능 평가
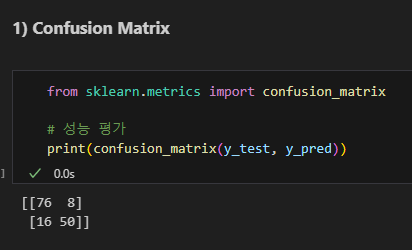
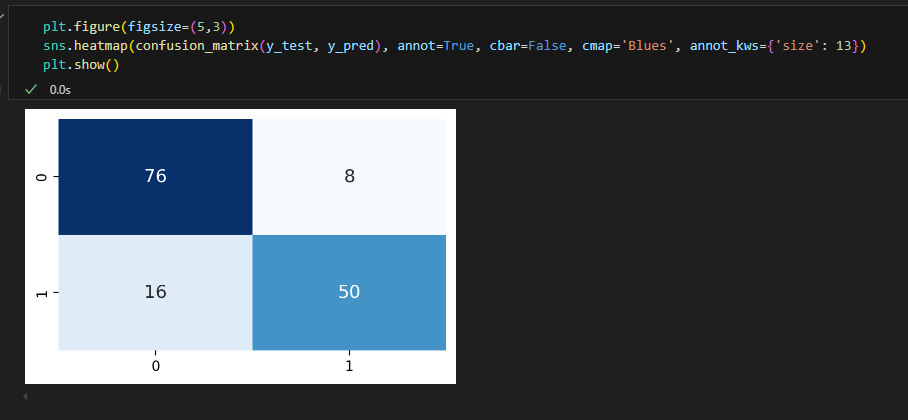
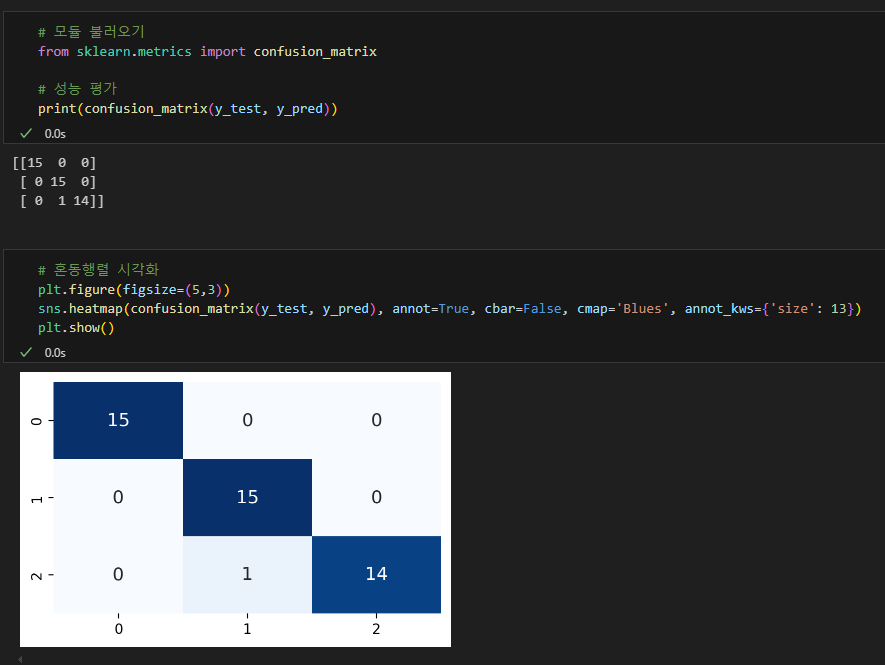
혼동 행렬
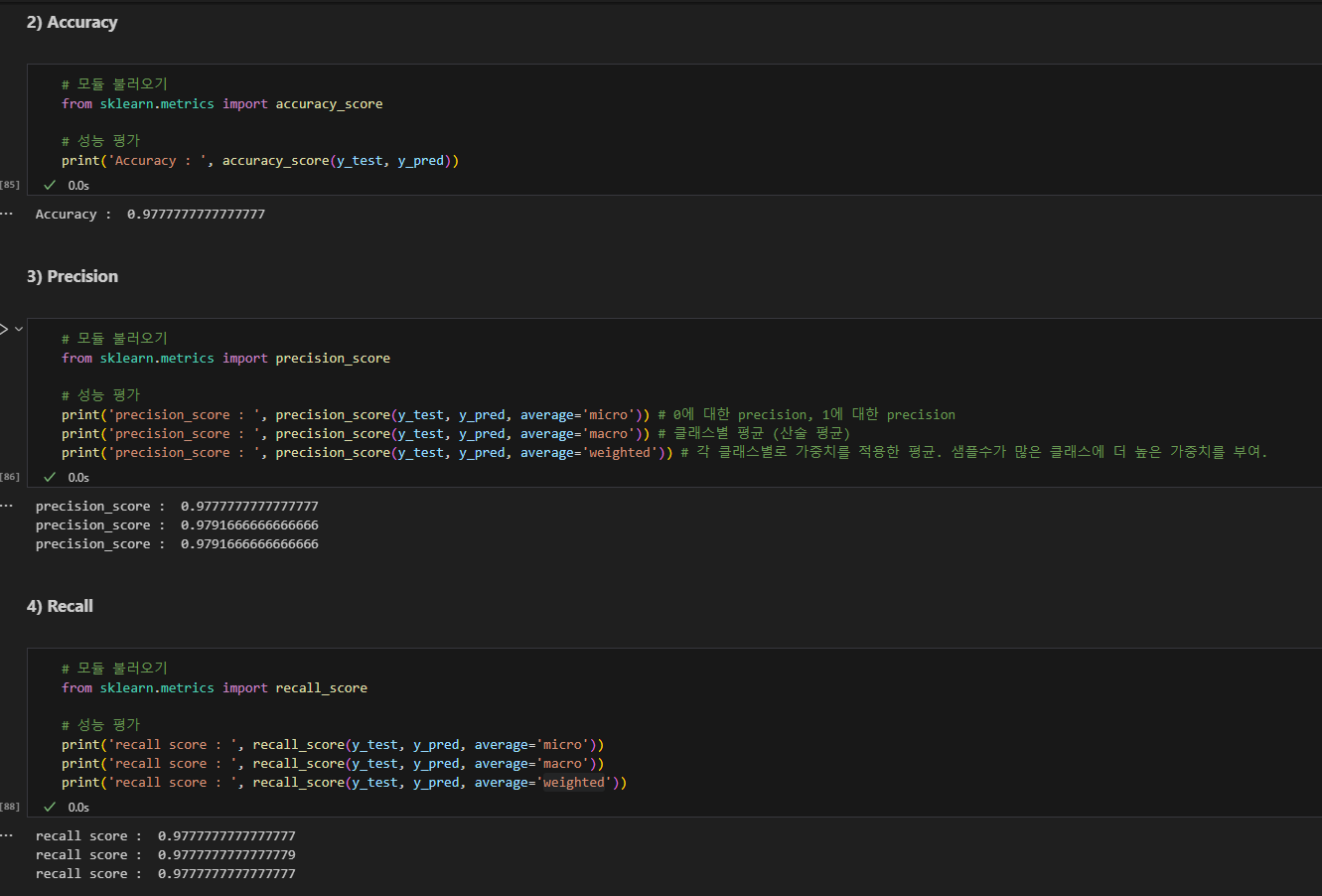
Accuracy
Precision 정밀도
(기본값 binary. positive에 대한 정밀도)
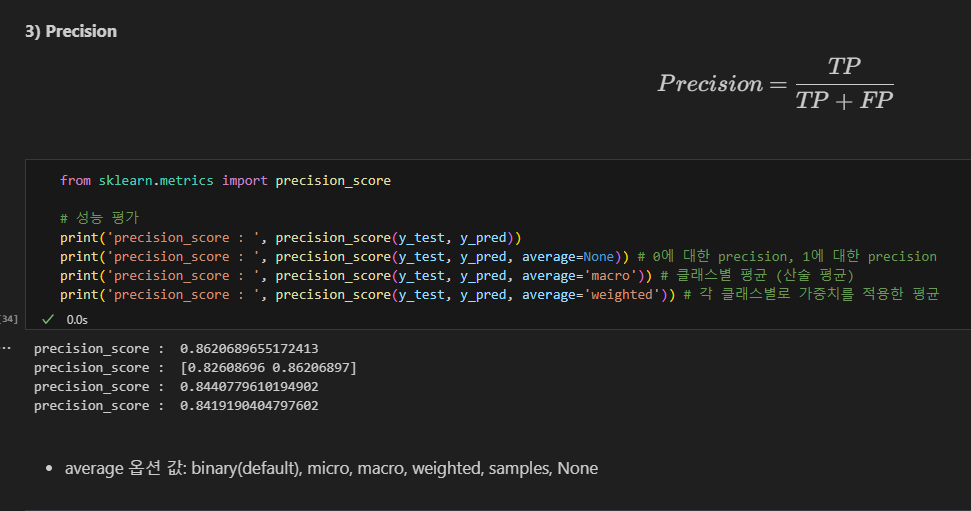
average=None : 0에 대한 precision, 1에 대한 precision
average='macro' : 클래스별 평균 (산술 평균)
average='weighted' : 각 클래스별로 가중치를 적용한 평균. 샘플수가 많은 클래스에 더 높은 가중치를 부여.
Recall 재현율
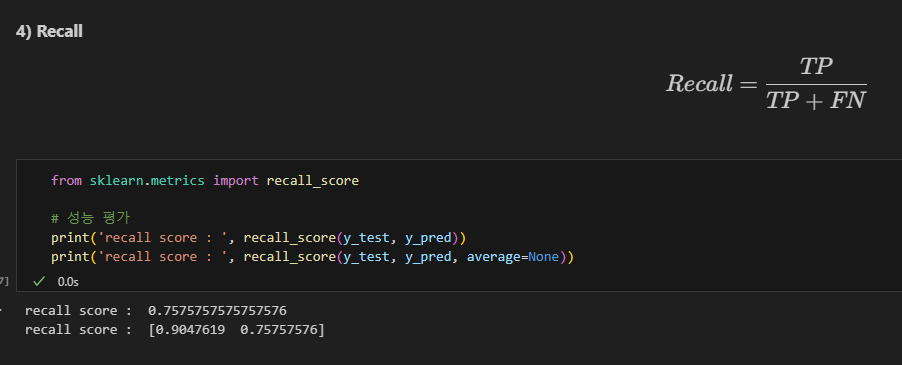
F1-score
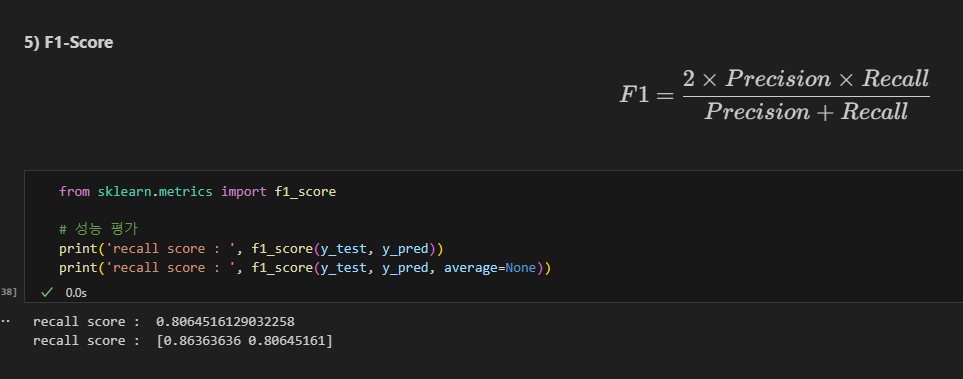
Classification report
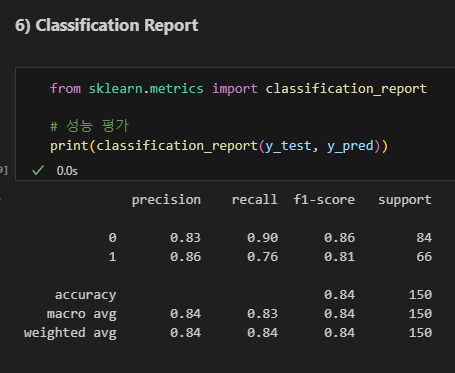
micro avg : 클래스별 샘플 갯수를 고려하지 않고, precision, recall, f1-score의 단순 평균.
weighnted avg : 샘플 갯수에 따라 가중 평균 계산
SVM
아이리스 식별
다중 클래스 분류에서는 binary(이진분류)로 하면 안됨.
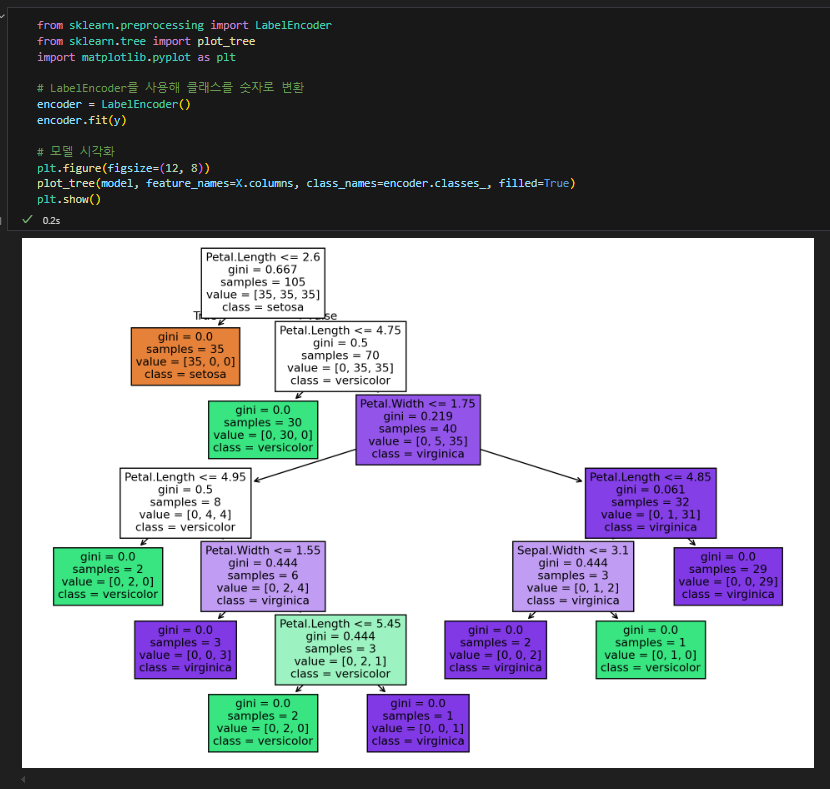
decision tree로 확인 (지니계수, 균일성)
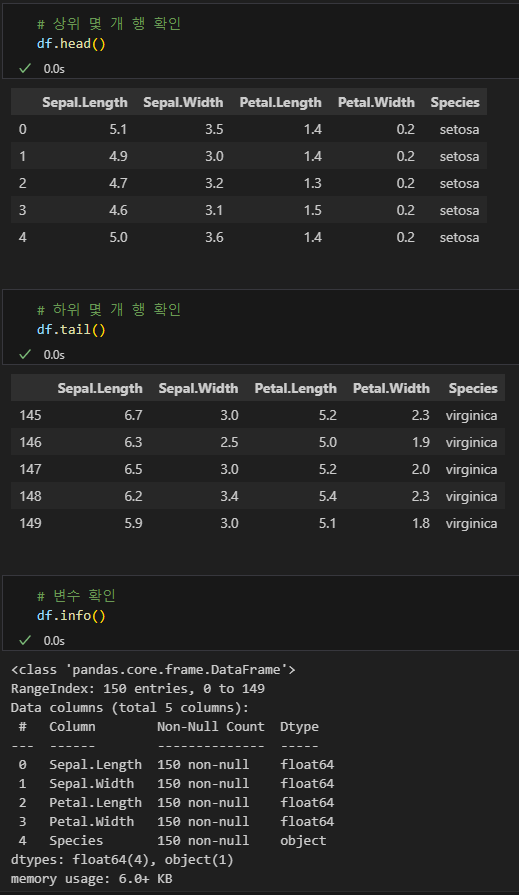
데이터 확인
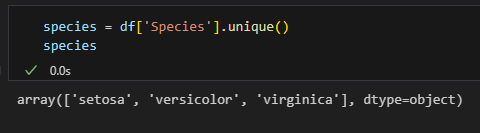
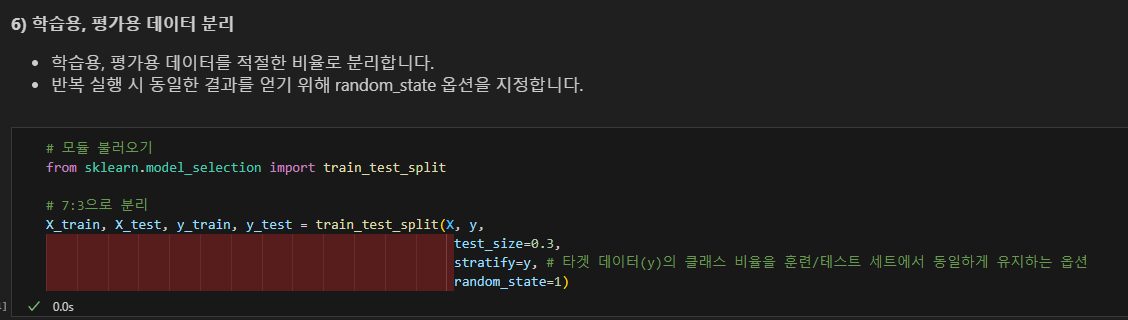
데이터 분리
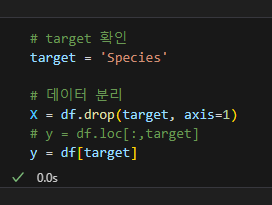
stratify=x로 균일성 제어
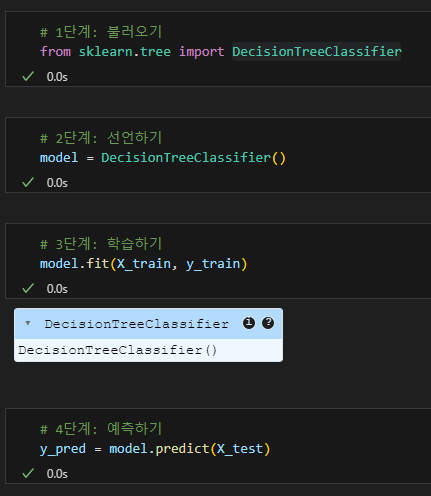
혼동 행렬 그리기
정확도, 정밀도, 재현율
F1, Classificaiton Report
지니계수도 구해봄
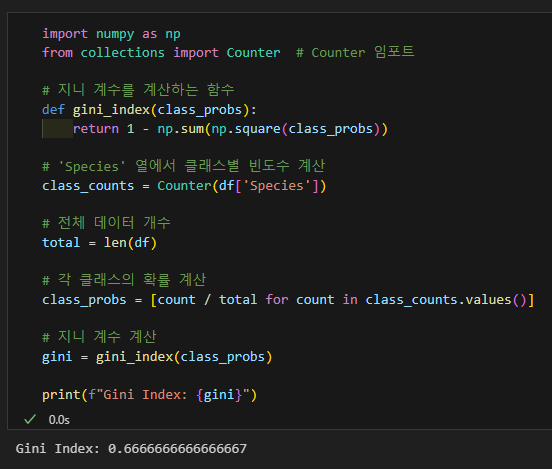
지니계수 0.5 이상: 높은 불순도를 나타냄. 데이터가 여러 클래스로 고르게 분포하고 있을 때, 즉 불균등하게 분포되어 있을 때 이 값에 가까워짐.
1.2. 알고리즘
다중 회귀
다중공선성 문제를 해결하기 위해 변수 선택이나 차원 축소 등의 기법을 활용
모델 학습을 위한 경사하강법 등 참조
회귀계수
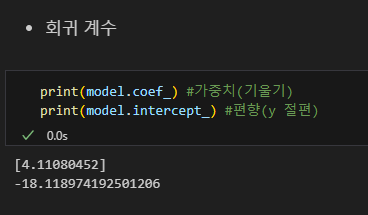
회귀계수 (Coef.):
- 관계의 세기: 회귀계수는 독립 변수와 종속 변수 사이의 관계의 강도를 나타냄. 예를 들어, 회귀계수가 0.7049이면, 독립 변수가 1만큼 증가할 때 종속 변수는 약 0.7049만큼 증가하는 경향이 있다는 의미.
- 방향: 이 값은 독립 변수와 종속 변수 사이의 상관 관계의 방향도 나타냄. 양수인 경우 독립 변수와 종속 변수가 양의 상관관계를 가지며, 음수인 경우에는 음의 상관관계를 가짐.
편향 (Intercept):
- 기준점 제공: 편향은 모델이 예측을 할 때, 독립 변수들이 모두 0일 때 종속 변수의 값을 제공함. 이는 모델이 "기준선"을 설정하는 데 중요함. 예를 들어, 모든 입력 값이 0일 때 종속 변수의 기본값이 얼마인지를 알 수 있음.
- 조정 역할: 편향은 모델이 실제 데이터를 잘 설명하도록 조정하는 역할을 함. 만약 모델이 편향을 고려하지 않는다면, 예측값이 실제 데이터에서 벗어나게 될 수 있음.
예측과 모델 평가:
- 회귀계수와 편향을 함께 사용하면, 주어진 독립 변수 값들에 대해 종속 변수의 예측 값을 정확히 구할 수 있음. 예측값을 구하는 방정식은
y = (회귀계수) * X + (편향)형태입니다. 이를 통해 새로운 데이터를 예측하거나 모델이 얼마나 정확한지 평가할 수 있음.
결론:
회귀계수와 편향은 모델을 정의하고 예측을 가능하게 해주는 핵심적인 요소. 각각의 값은 모델이 학습한 데이터의 패턴을 이해하고, 그 패턴을 기반으로 예측을 수행하는 데 필요. 이 값을 따로 구하는 이유는 모델을 완성하고 예측을 실제로 적용하기 위해 필요한 값이기 때문.
x가 많은 경우
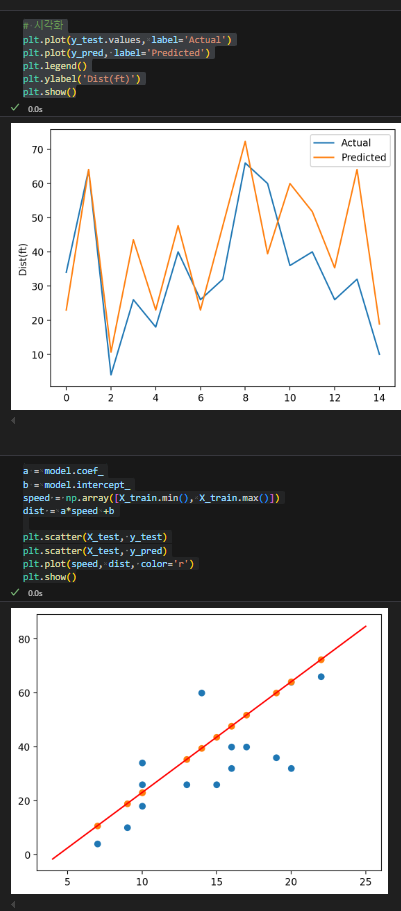
각 변수별 가중치 시각화하기
편향(y절편)까지 시각화
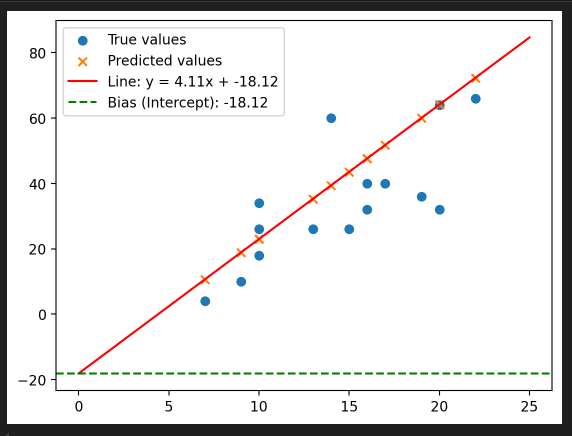
편향은 가중치의 일부임.
값이 같다고 하더라도 편향(intercept)이 달라지는 이유:
가정이 달라지는 경우.
모델 훈련 셋팅이나 초기화 차이.
Ridge나 Lasso 회귀와 같은 정규화 기법을 사용하면 모델의 복잡도를 제어하려고 할 때, 편향 값도 달라질 수 있음. 특히 정규화가 강하게 적용되면 편향이 작아지거나 달라질 수 있음.
해결법: 정규화를 사용하지 않고 실험하거나, 정규화 강도를 조정하여 모델이 과도하게 제약되지 않도록 함.
스케일 차이: 특성들이 서로 다른 스케일을 가지고 있을 때, 모델이 데이터를 처리하는 방식에 따라 편향 값이 달라질 수 있음. 예를 들어, 특성들이 표준화(standardization)나 정규화(normalization)되었는지 여부에 따라 편향이 달라질 수 있음.
해결법: 동일한 방식으로 데이터를 전처리하고, 특히 특성의 스케일을 맞추는 작업을 일관되게 수행.
훈련 데이터가 달라지는 경우.
학습률(learning rate)이나 최적화 방법 차이
학습률 조정: 최적화 알고리즘에서 학습률이 너무 크거나 작으면, 모델이 수렴하는 방식이 달라질 수 있음. 학습률이 너무 크면 모델이 최적의 값에 도달하지 못하고, 너무 작으면 수렴 속도가 매우 느려질 수 있음.
해결법: 적절한 학습률을 선택하고, 학습률 조정(예: 학습률 스케줄링)을 사용하여 모델이 잘 수렴하도록 해야함.
모델의 가정 차이
선형 회귀 가정: 선형 회귀는 데이터가 선형적 관계를 갖는다고 가정함. 데이터에 비선형성이 포함되거나 특성 간의 관계가 복잡한 경우, 모델이 완벽하게 학습되지 않으면 편향이 다르게 나올 수 있음.
해결법: 선형 회귀 모델이 적합한지 확인하고, 비선형 모델을 사용해야 하는 경우 다른 알고리즘(예: 결정 트리, 신경망 등)을 고려.
상수 추가
편향의 정의: 편향은 종종 모델에 추가된 상수 항으로, 학습 과정에서 데이터가 0일 때 예상되는 값. 학습이 잘못되어 모델이 0이 아닌 다른 값에서 시작하게 되면, 편향도 달라질 수 있음.
해결법: 학습 과정에서 편향이 잘 학습되도록 정확한 초기화 및 정규화 기법을 사용하여 편향이 과도하게 변경되지 않도록 함
