[프로그래머스] 스티커 모으기(2)

스티커 모으기(2)

Programers

문제 설명

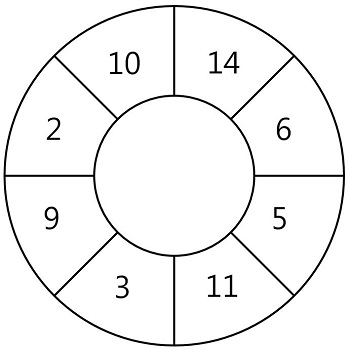
N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.

원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.
예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

제한 사항

• sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
• sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
• 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

작성 코드

def solution(sticker):
    answer = 0
    # 스티커가 3장 이하라면, 어떻게 하든 하나만 얻을 수 있음.
    if len(sticker)<=3:
        return max(sticker)
    dp1=[0]*len(sticker) # 첫 수를 담는 경우 (마지막 원소를 하지 않음)
    dp2=[0]*len(sticker) # 안 담는 경우 (마지막 원소도 가능)
    # 선언된 dp에 0의 값과 1의 값 초기화
    dp1[0]=sticker[0]
    dp1[1]=sticker[0]
    # 2부터 마지막 바로 전까지 반복문을 시작하는 데,
    for i in range(2,len(sticker)-1):
        # 선택지를 주는 데, 바로 앞의 숫자를 더한 것이 더 큰지,
        # 아니면 자신과 2번 앞의 합을 더한 값이 더 큰지 비교하여 선택함.
        # ex) sticker= [6,1(상관없음),10,14,x],dp1=[6,6,16,20, ] 라고 할 때,
        # x가 2라면, 14를 더한 값 dp[3]=20이고, dp[4]=dp[2]+sticker[4]=18이므로, 20이 더 큰 수
        # x가 4보다 큰 10이라면, dp[3]=20, dp[4]=dp[2]+sticker[4]=26 이므로 26이 더 크다.
        # 해당 방식을 반복해 가며, 앞의 값과 자신을 더한 값 중 어느 것이 큰지 지속적으로 선택
        dp1[i]=max(dp1[i-1],dp1[i-2]+sticker[i])
    # 첫번째 항을 넣지 않은 dp2 초기화
    dp2[0]=0
    dp2[1]=sticker[1]
    # 2부터 마지막까지 반복문
    for i in range(2,len(sticker)):
        # dp1과 같이 작동
        dp2[i]=max(dp2[i-1],dp2[i-2]+sticker[i])
    # 두 경우중 큰값을 return 해줌
    return max(dp1[-2],dp2[-1])