그래프의 정점에서 모든 정점까지의 최단 거리를 구하는 알고리즘이다.
우선순위 큐(=힙 트리) 등을 이용하면서 더욱 개선되어 O((V + E)log V)(V는 정점의 개수, E는 한 정점의 주변 노드)의 시간복잡도를 가진다.
알고리즘
다익스트라 알고리즘은 다음과 같다.
- 출발점으로부터의 최단거리를 저장할 배열 d[v]를 만들고, 출발 노드에는 0을, 출발점을 제외한 다른 노드들에는 매우 큰 값 INF(ex. int.MaxValue)을 채워넣는다.
- 현재 노드를 나타내는 변수 A에 출발 노드의 번호를 저장한다.
- A로부터 갈 수 있는 임의의 노드 B에 대해, d[A](기존 거리) + P[A]B}(A와 B 사이의 거리) 와 d[B]의 값을 비교한다. INF와 비교할 경우 무조건 전자가 작다.
- 만약 d[A] + P[A][B]의 값이 더 작다면, 즉 더 짧은 경로라면, d[B]의 값을 이 값으로 갱신시킨다.
- A의 모든 이웃 노드 B에 대해 이 작업을 수행한다.
- A의 상태를 “방문 완료”로 바꾼다. 그러면 이제 더 이상 A는 사용하지 않는다.
- “미방문”상태의 모든 노드들 중 출발점으로부터의 거리가 제일 짧은 노드 하나를 골라서 그 노드를 A에 저장했다.
- 도착 노드가 “방문 완료” 상태가 되거나, 혹은 더 이상 미방문 상태의 노드를 선택할 수 없을 때 까지 3 ~ 7의 과정을 반복한다.
이 작업을 마친 뒤 도착 노드에 저장된 d 의 값이 바로 A로부터의 최단 거리이다. 만약 이 값이 INF라면, 중간에 길이 끊긴 것을 의미한다.
7번 단계에서 거리가 가장 짧은 노드를 고르는 것은 우선순위 큐를 활용하면 비용을 줄여 계산할 수 있다.
그림 설명
S = 방문한 노드들의 집합
d[N] = A → N 까지 계산된 최단 거리
Q = 방문하지 않은 노드들
A에서 F까지의 최단 거리를 구해보자
1. 다익스트라 알고리즘은 아직 확인되지 않은 거리는 전부 초기값을 무한으로 잡는다
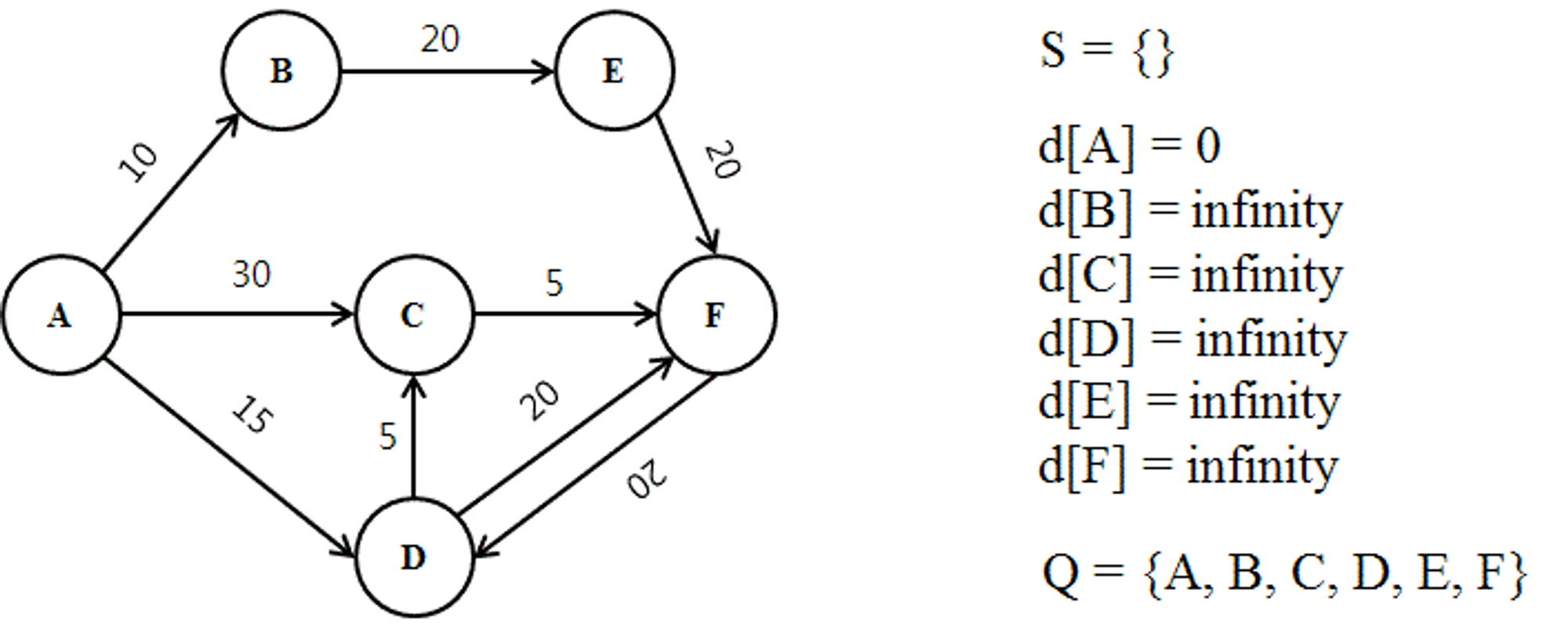
출발지와 출발지의 거리는 항상 0을 가진다. 출발지를 A로 설정했기 때문에 d[A]는 0이 된다.
출발지를 제외한 노드들은 아직 확인되지 않았기에 무한한 값으로 설정해둔다.
2. 루프를 돌려 이웃 노드를 방문하고 거리를 계산한다.
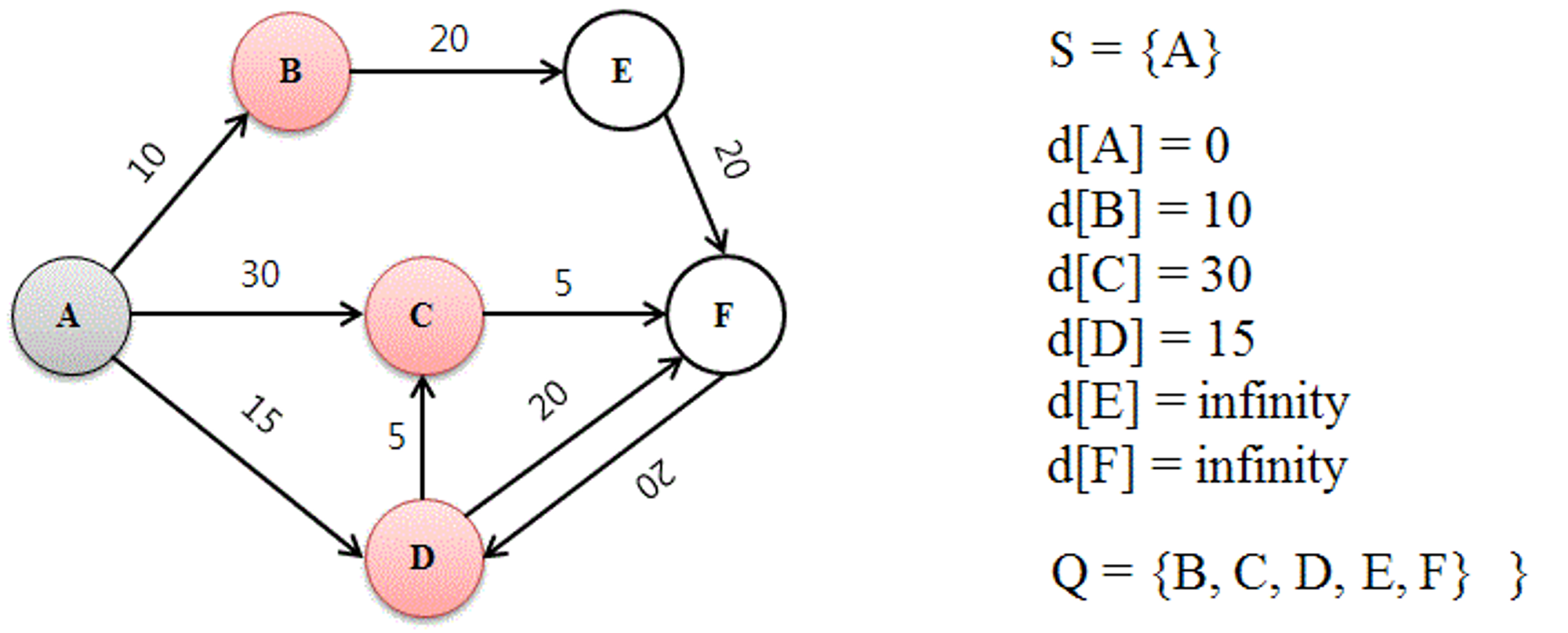
가장 먼저, 거리가 최소인 노드 (d[N]이 최소값인 노드 N)를 Q(방문하지 않은 노드의 집합)에서 제거하고, 그 노드를 S(방문한 노드의 집합 및 최소 경로)에 추가한다. 이는 즉, 노드 N을 ‘방문한다’ 라는 의미가 된다.
이후, 방문한 노드 N과 연결된 모든 이웃 노드와의 거리를 측정하여 d[N](=출발지로부터 N까지 계산된 최소 거리값) + N과 이웃노드 간의 거리값) 이 계산된다. 새로 계산된 값이 기존의 저장된 값이 작은 경우에만 d[N]을 갱신한다.
예를 들어 초기화 직후의 첫 루프에서 시작 정점으로부터의 거리가 최소인 노드는 A(자기 자신) 이므로, 노드 A를 방문하여 Q엣서 제거하고 S에 추가하게 된다. 다만, 지금은 첫 번째 루프만을 끝낸 상태이므로, 단순히 0 + (이웃 노드와 출발지 사이의 거리값) = (출발지와 이웃 노드 간의 거리값)이 각 이웃 노드까지의 거리값으로 기록된다.
3. 첫 루프 이후의 그래프의 상태가 업데이트되는 방식
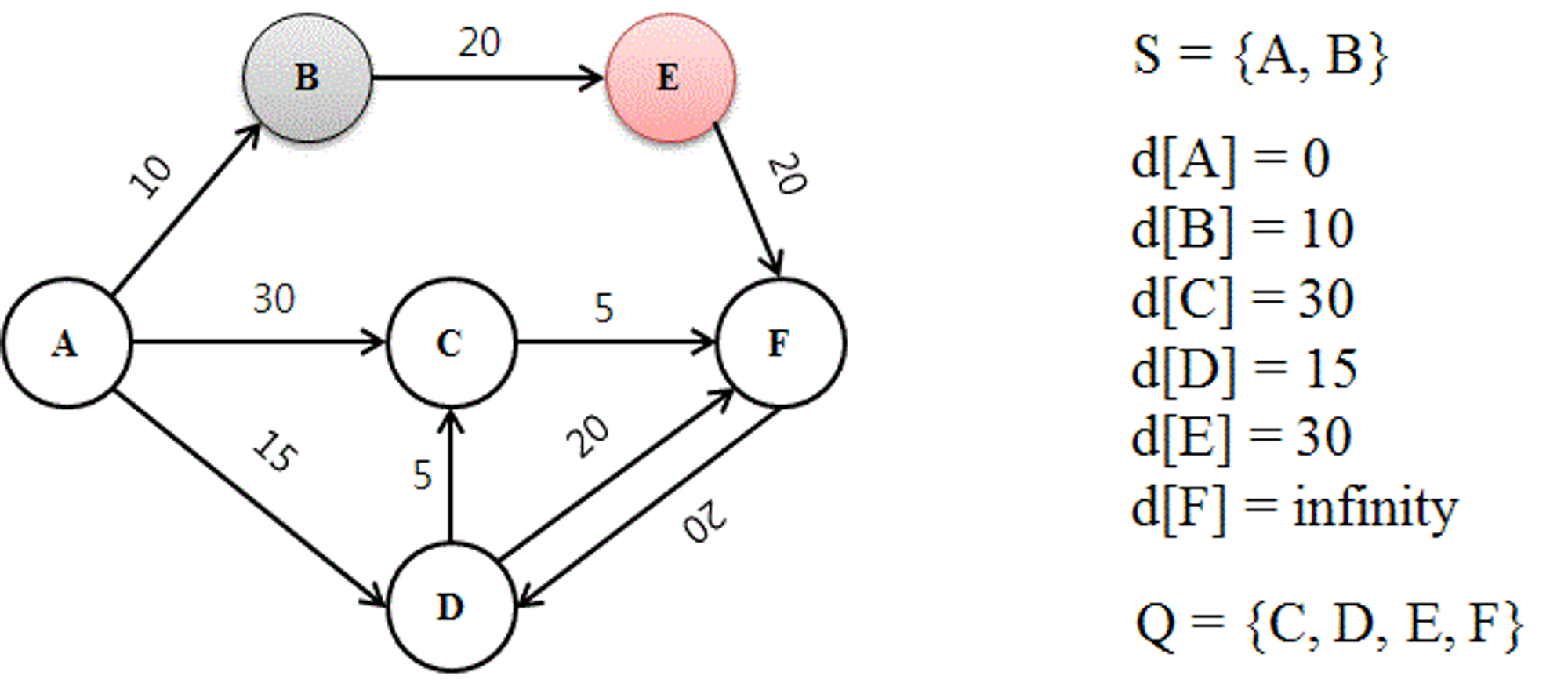
이제부터 루프가 반복적으로 실행된다.
이전에 설명했듯이, 방문할 노드는 Q에 남아있는 노드들 중 d[N] 값이 제일 작은 것으로 선택된다. 따라서 d[B]가 10으로 제일 작은 값을 가지므로 (이 단계를 우선순위 큐로 체크) B를 방문하여 S에 추가하고 Q에서 제거한다.
이제 B의 이웃 노드들을 모두 탐색하여 거리를 재고 d[N]에 기록하다. B의 이웃 노드는 E뿐이므로, d[E] 값이 무한에서 d[B] + (B로부터 E까지의 거리값 20) = 30으로 업데이트 된다. 여기서 d[B] 값을 더하는 이유는 출발지로부터 해당 노드까지의 거리값을 재기 위해서다.
4. 더 빠른 경로를 발견한 경우
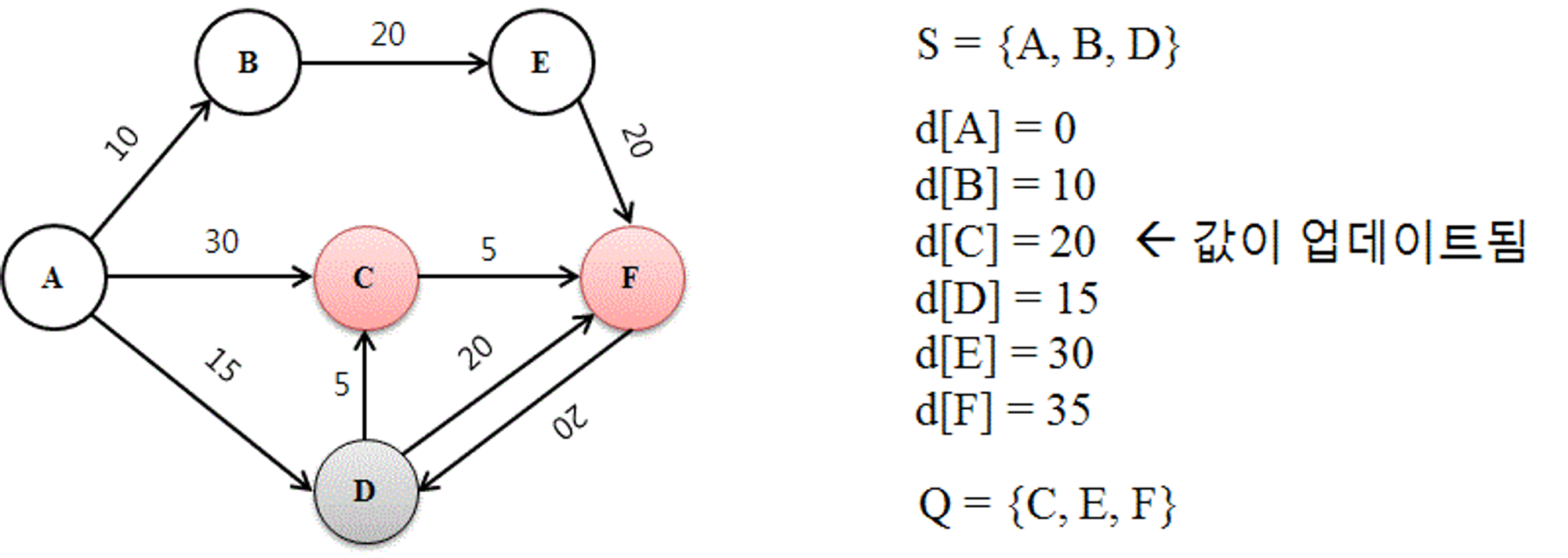
세 번째 루프에서 선택 방문되는 D이다. 두 번째 루프를 마친 후 Q의 원소 중에서 제일 낮은 N의 값을 가진 것이 D이기 때문이다. 따라서 세번째 루프를 맞친 뒤인 위의 그림에서도 S에 D가 추가되어 있는 것을 볼 수 있다.
이제 D의 이웃 노드들(C,F)의 거리를 잰 후, d[N] 값을 업데이트 한다. 이때 d[C]의 값은 A를 방문할 때 이미 계산되어 30으로 저장되어 있었으나, D를 방문하여 C와의 거리를 비교해보니 20으로 더 짧은 최단 경로가 발견되었다. 그러므로 d[C] 값을 20에서 20으로 변경한다.
5. 또 다른 반복 루프 상황
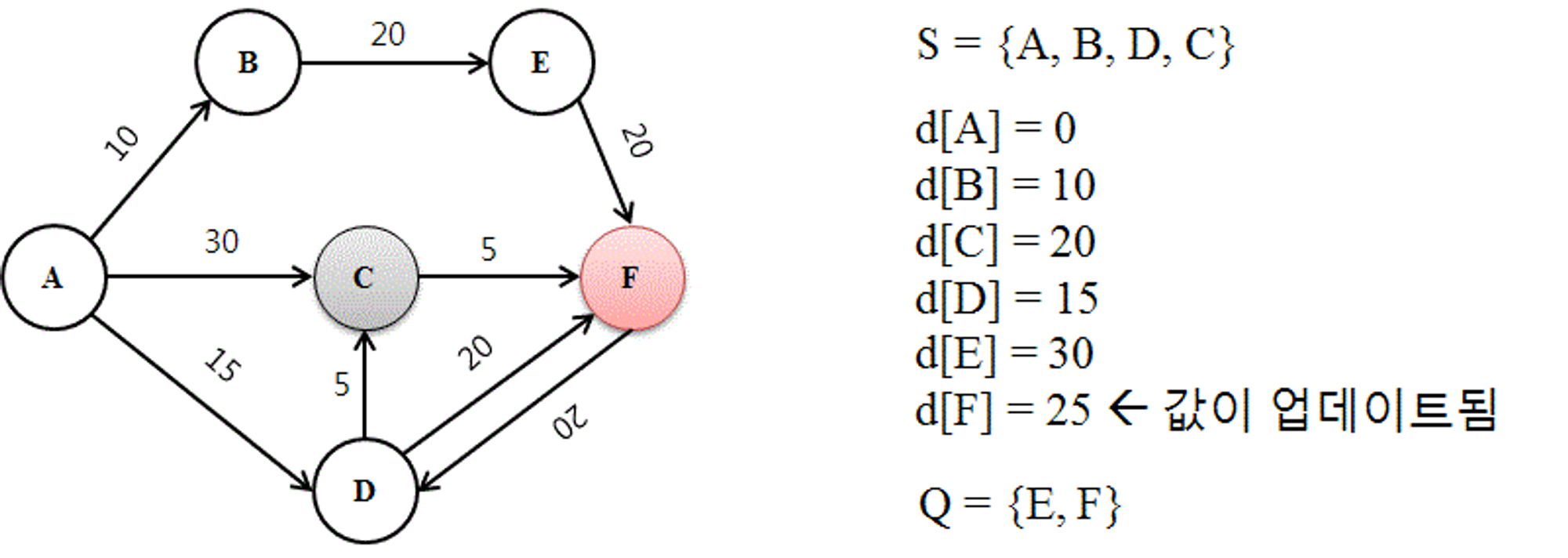
Q 에 남은 값 중 d[C] = 20 으로 거리가 가장 짧은 C를 방문한다.
다시 이웃 노드와 계산해서 d[F]를 더 짧은 거리 25로 업데이트 한다.
코드
이러한 다익스트라 알고리즘을 구현한다고 가정하자.
using System;
using System.Collections.Generic;
namespace Algorithm
{
public class Program
{
// 정렬기준을 만들어 주기 위해 필요한 Compare 함수 재정의
public class Mycompare : IComparer<List<int>>
{
// 비용 기준으로 오름차순
public int Compare(List<int> x, List<int> y)
{
if (x[0] == y[0]) return x[1] - y[1];
return x[0] - y[0];
}
}
public static int[,] dist = new int[20, 20]; //[시작노드, 도착노드] 거리 정보
public static List<List<int>>[] node = new List<List<int>>[20]; // 노드 정보
// 다익스트라 알고리즘
public static void Dijkstra(int sx)
{
// 우선 순위 queue를 의미하는 내부요소를 자동으로 정리해주는 자료구조
SortedSet<List<int>> pq = new SortedSet<List<int>>(new Mycompare());
dist[sx,sx] = 0;
pq.Add(new List<int>() { 0, sx });
while (pq.Count > 0) // 더 이상 방문 할 수 있는 곳이 없다
{
List<int> cnt = pq.First();
pq.Remove(cnt);
int cost = cnt[0]; // 거리 비용
int x = cnt[1]; // 현재 노드
if (dist[sx, x] < cost) continue; // 시작 위치에서 목적지까지의 거리 비교
for (int i = 0; i < node[x].Count; i++) // 현재 노드와 연결되어 있는 노드들 순회
{
int next = node[x][i][0]; // 연결 노드
int nCost = node[x][i][1] + cost; // 현재 거리 비용과 연결되어 있는 새 노드 거리 비용 합계
if (dist[sx,next] > nCost) // 새로 구한 값이 더 싸다면
{
dist[sx, next] = nCost;
pq.Add(new List<int>() { nCost, next });
}
}
}
}
public static void Main(String[] args)
{
//초기화
for (int i = 0; i < 20; i++) node[i] = new List<List<int>>();
// dist 배열 큰 값으로 맞춰줌
for(int i = 0; i < 20; i++)
for (int j = 0; j < 20; j++) dist[i, j] = 9999999;
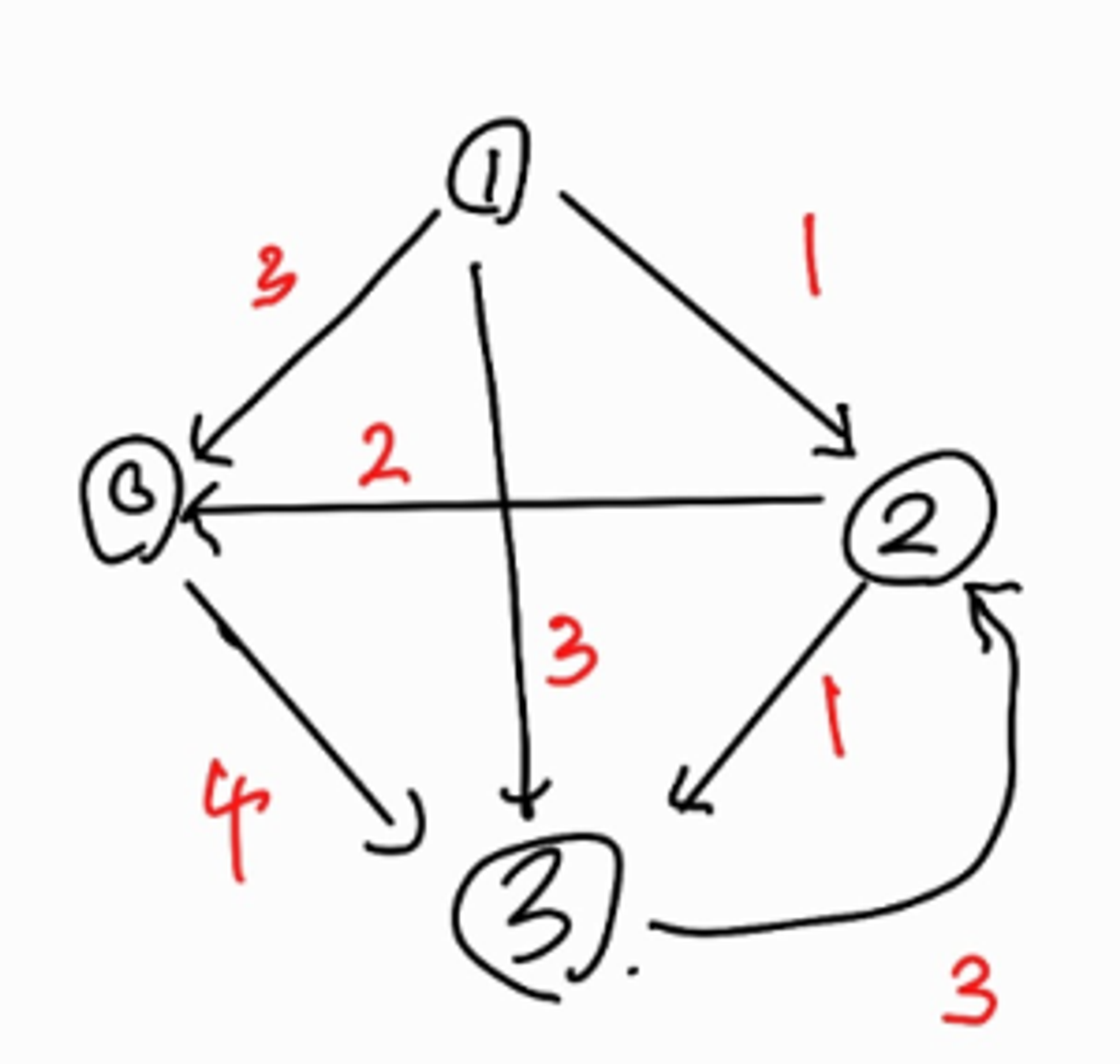
// 노드 정보 담기
node[0].Add(new List<int>(){3,4});
node[1].Add(new List<int>(){0,3});
node[1].Add(new List<int>(){2,1});
node[1].Add(new List<int>(){3,3});
node[2].Add(new List<int>(){0,2});
node[2].Add(new List<int>(){3,1});
node[3].Add(new List<int>(){2,3});
for(int i = 0; i <= 3; i++) Dijkstra(i); // 함수 실행
for (int i = 0; i <= 3; i++)
{
for (int j = 0; j <= 3; j++)
{
if (i == j) continue;
Console.WriteLine($"{i}번 노드에서 {j}번 노드로 갈 때의 최소 비용 = {dist[i,j]}");
}
}
}
}
}참고 : https://namu.wiki/w/%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BC%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://howudong.tistory.com/335
https://ansohxxn.github.io/algorithm%20lesson%202/chapter4-5/
