백준 / 골드 5 / 12865. 평범한 배낭

생각해봅시다!

• 흔히 0-1 배낭 문제라고도 불리는, 대표적인 DP 문제입니다.
  • 전에 봤던 배낭 문제와 다르게, 각 물건을 쪼개서 넣을 수 없습니다.
  • 각 물건은 전체를 다 담거나(1) 아예 빼야 합니다(0). 그래서 0-1 배낭 문제라는 이름이 붙었고요.
• 결국에는 한 물건씩 확인하면서 해당 물건을 넣을지 안 넣을지 고려하는 게 중요합니다.
• DP는 항상 수식의 항연 없이는 설명하기가 힘든 것 같아요... 직접 그리고 계산하시면서 따라오시는 걸 추천...

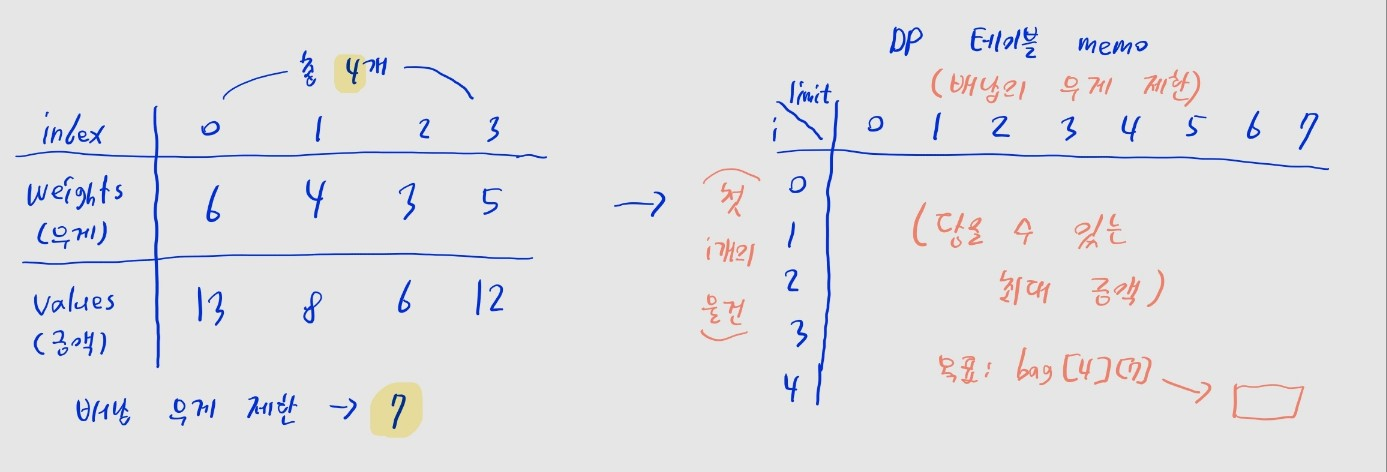
DP 테이블 정의하기

• 결국엔 무게제한이 있는 배낭에 담을 수 있는 최대 금액을 구해야 됩니다.
  • 각 물건의 무게는 weights 리스트에, 금액은 values 리스트에 저장되어 있다고 가정합시다.
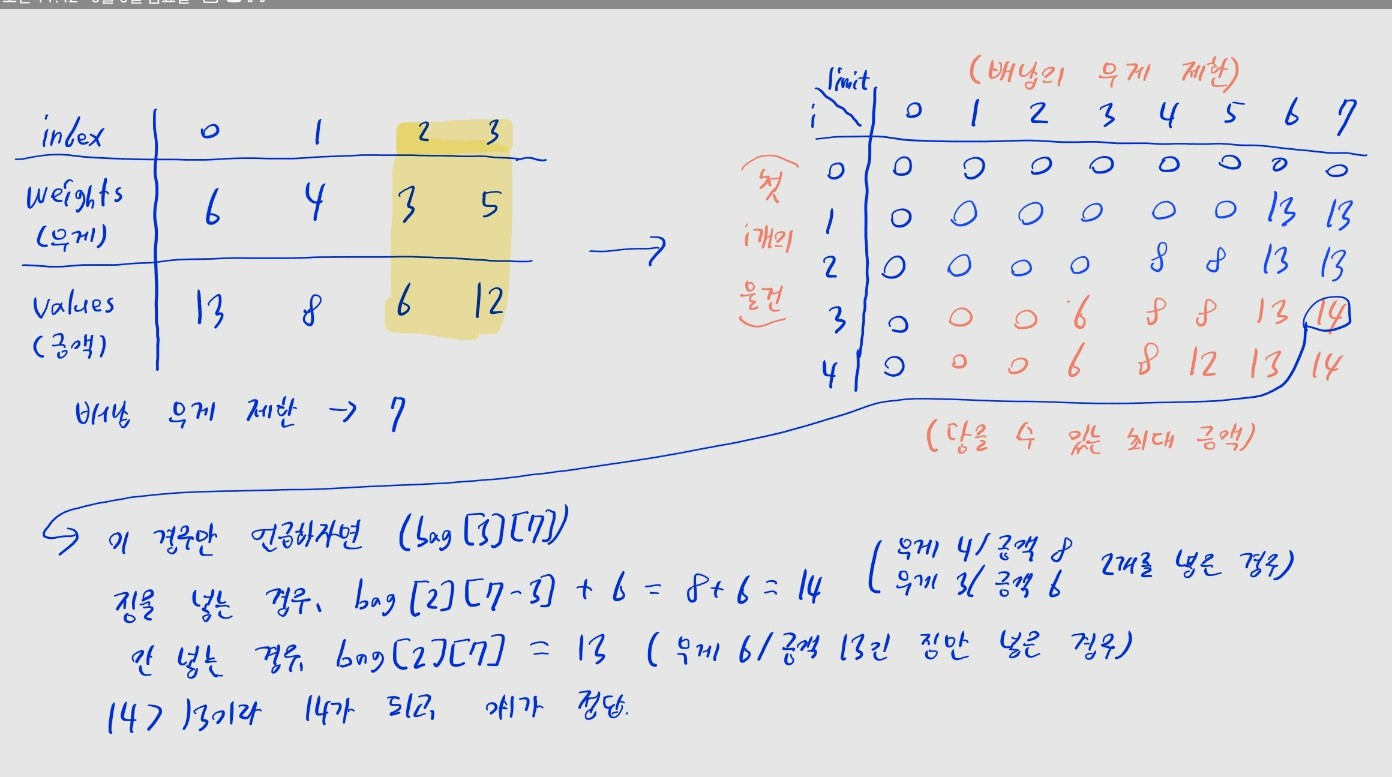
• 2차원 배열 bag를 정의합니다.
  • bag[i][j]에는 무게 제한이 j인 배낭에 첫 i개의 물건을 담거나 담지 않을 수 있을 때, 가능한 최대 금액을 저장합니다.
• 예제에서는 짐의 개수가 4개이고 배낭의 무게제한이 7이므로, bag[4][7]을 찾아야 합니다.
  • DP 테이블도 행 (4 + 1 = 5)개, 열 (7 + 1 = 8)개가 되도록 초기화하면 됩니다.

기저 조건

• 일단 바로 채울 수 있는 칸부터 채워봅시다.

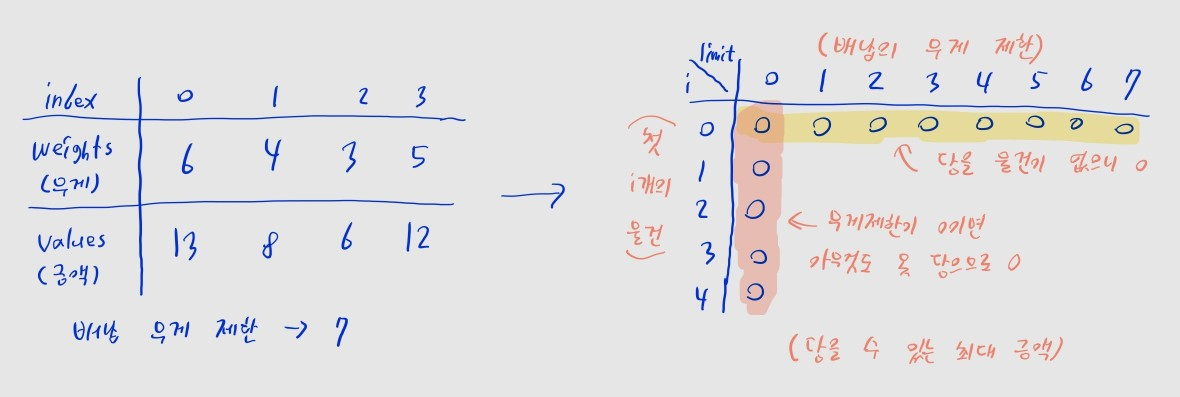
i == 0일 때

• i == 0이면 물건이 없으므로, 당연히 배낭에 넣을 수 있는 최대 금액은 0원입니다.

j == 0일 때

• j == 0이면 배낭의 무게제한이 0이므로, 당연히 아무것도 담을 수 없으니 최대 금액은 0원입니다.

나머지 칸 채우기

• 이제 i >= 1 and j >= 1일 때를 채워봅시다.
• 편의상 앞선 예제를 풀어보면서 진행하겠습니다. 한 물건씩 확인하면서 테이블을 채워 나갑시다.

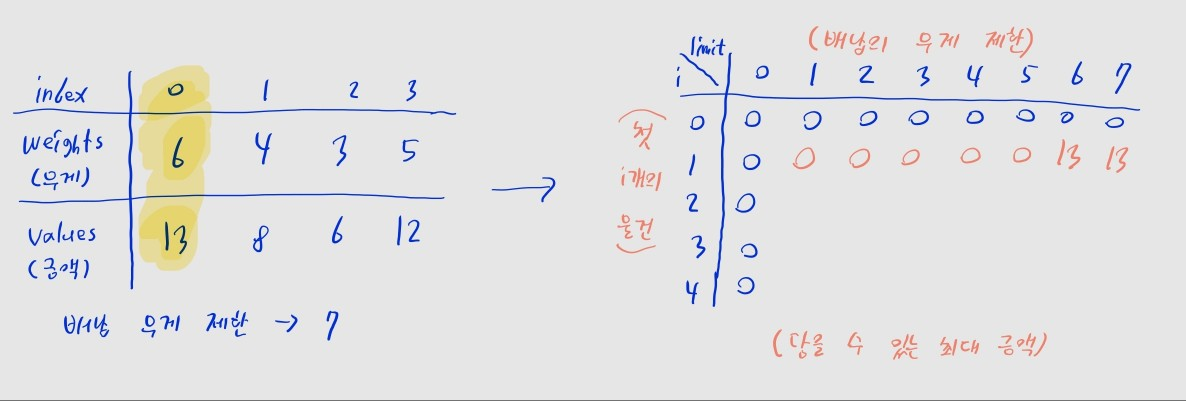
i == 1 (1행)

• 첫 물건의 무게는 6, 금액은 13입니다.
• j열은 배낭의 무게 제한이 j일 때를 뜻한다고 했었죠?
• 배낭의 무게 제한이 6보다 작으면 물건을 담을 수 없습니다. bag[1][0] ~ bag[1][5]까진 0으로 채웁니다.
• bag[1][6] ~ bag[1][7]까진 물건을 담을 수 있으므로, 13으로 채웁니다.

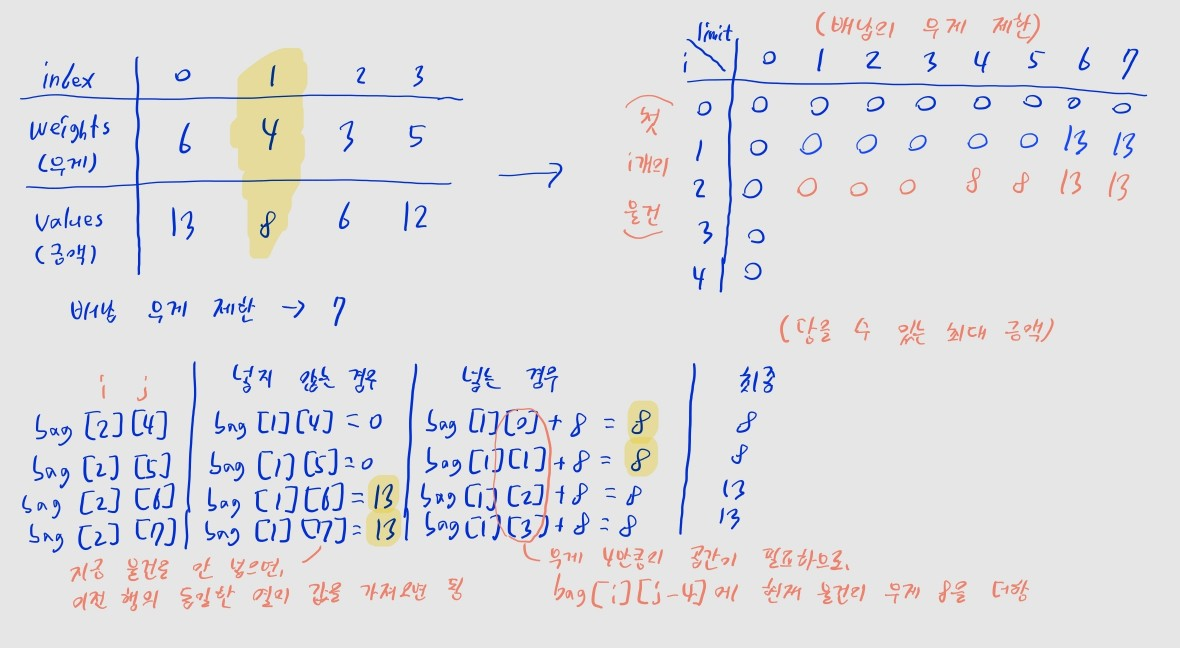
i == 2 (2행)

• 둘째 물건의 무게는 4, 금액은 8입니다.
• 배낭의 무게 제한이 4 미만일 땐 물건을 담을 수 없습니다. bag[2][0] ~ bag[2][3]까진 이전 행의 값을 그대로 bag[1][0] ~ bag[1][3]의 값을 복사합니다.
• bag[2][4]부터는 물건을 넣을 수도 있고, 안 넣을 수도 있습니다.
  • 물건을 넣지 않는 경우, 이전 행에서 같은 무게 제한일 때의 최대 금액인 bag[1][4]의 값을 가져옵니다. 물건을 더 안 넣었으니 금액이 바뀌지 않습니다.
  • 물건을 담은 경우, 배낭에 무게 4만큼의 공간이 필요합니다. 즉 남는 무게 4 - 4 = 0일 때의 최대 금액에, 현재 물건의 금액 8을 더합니다. 즉 총 금액은 이전 행의 bag[1][0]에 8을 더한 값이 됩니다.
  • 두 값을 비교해서 더 큰 값을 선택합니다.
• bag[2][j] (5 <= j <= 7)도 마찬가지로
  • 물건을 넣지 않는 경우, 총 금액은 이전 행의 bag[1][j]와 동일합니다.
  • 물건을 넣는 경우, 무게 4만큼의 공간이 필요하므로, 총 금액은 이전 행의 bag[1][j - 4]에 8을 더한 값이 됩니다.
  • 두 값을 비교해서 더 큰 값을 선택합니다.

i == 3 (3행), i == 4 (4행)

• 같은 규칙대로 나머지 행을 채워 나갑니다.
• 현재 넣을 물건의 무게와 금액은 각각 values[i - 1], weights[i - 1]입니다. 편의상 curr_v, curr_w로 치환하겠습니다.
• 배낭의 무게 제한 j가 현재 물건의 무게보다 작은 경우 (j < curr_w)
  • 물건을 못 넣으므로, bag[i][j] = bag[i-1][j]. 이전 행 값을 그대로 가져옵니다.
• 배낭의 무게 제한 j가 현재 물건의 무게 이상인 경우 (j >= curr_v)
  • 물건을 넣지 않는 경우,bag[i - 1][j]. 이전 행 값을 그대로 가져옵니다.
  • 물건을 넣는 경우, bag[i - 1][j - curr_w] + curr_v. 이전 행에서 현재 무게를 뺀 열의 값에다가, 현재 금액을 더합니다.
  • 두 값 중 최댓값을 구합니다.
• 즉 bag[i][j] = max(bag[i - 1][j], bag[i - 1][j - curr_w] + curr_v)의 점화식을 만들 수 있습니다.

풀이

# 물품수 N, 최대무게 K
N, K = map(int, input().split())
bag = [[0] * (K + 1) for _ in range(N + 1)]

for i in range(1, N + 1):
    # 현재 짐의 무게, 금액
    curr_w, curr_v = map(int, input().split())
    
    # 각 행의 열 채우기
    for j in range(1, K + 1):
        # 배낭의 무게제한이 현재 무게보다 작음
        if j < curr_w:
            # 넣지 못함 (이전 행의 값)
            bag[i][j] = bag[i-1][j]
        
        # 배낭의 무게제한이 현재 무게 이상
        else:
            # 넣거나 (현재 무게를 비웠을 때 최대 금액) + (현재 금액)
            in_result = bag[i-1][j-curr_w] + curr_v
            
            # 넣지 않거나 (이전 행의 값)
            out_result = bag[i-1][j]
            
            # 더 큰 값을 선택
            bag[i][j] = max(in_result, out_result)
            
# 모든 물건 + 무게제한 K일 때
print(bag[N][K])

시간 복잡도

• 물건의 수가 $N$개, 최대 무게가 $K$개일 때, DP 테이블의 $(N + 1) \times (K + 1)$개의 값을 구하므로 결국 $O(N \times K)$
• $N \leq 100$, $K \leq 100,000$이므로 최대 $10,000,000$. 2초라서 그 안엔 통과합니다.