정글 5주차 과제로는 기본적으로 제공하는 자료구조 구조체 및 함수를 이용해서, 다양한 응용문제를 풀게 됩니다.

블로그에서 모든 응용문제를 다루기보다는, 기본 제공 코드의 구조체 및 함수의 동작 원리만 분석할 계획입니다. 사실 이걸 제대로 알면 응용문제를 푸는 게 더 수월할 거에요.

• 따라서 코드는 제가 직접 작성하진 않았고(약간의 수정은 있음) 정글에서 제공한 코드입니다. 물론 주석, 설명이랑 그림은 제가 추가했습니다!

이진 (탐색) 트리에 대한 상세한 설명은 이 글을 참고해주세요

본 글의 전체 소스 코드는 깃허브에 올려 두었습니다

구조체 선언

// 각 노드를 나타내는 구조체 Node
typedef struct _bstnode{
	int item;                   // 노드에 저장된 값
	struct _bstnode *left;      // 왼쪽 자식 노드를 가리키는 포인터
	struct _bstnode *right;     // 오른쪽 자식 노드를 가리키는 포인터
} BSTNode;

// 이진 탐색 트리를 나타내는 구조체 BST
typedef struct _bst{
    struct _bstnode *root;      // 머리 노드를 가리키는 포인터
} BST;

• 연결 리스트의 노드는 다음 노드를 가리킬 포인터 1개만 필요했다면
• 트리의 노드는 왼쪽 / 오른쪽 자식 노드를 각각 가리킬 포인터 2개가 필요함
  • left, right 포인터 2개를 둠
  • 자식이 없는 리프 노드인 경우, left와 right의 값은 NULL (널 포인터)
• 루트 노드의 위치를 모르면 트리를 탐색할 수 없음
  • 따라서 BST 구조체에, 루트 노드를 가리키는 BSTNode *형 포인터 root를 둠

⚠️ 엄밀히 말하면 root, left, right의 포인터에는 가리키는 노드 구조체의 주소가 저장됩니다. 다만 본 글에서는 간결성을 위해 (root / left / right에 노드를 저장)과 같은 방식으로 표현하겠습니다. 착오가 없길 바랍니다.

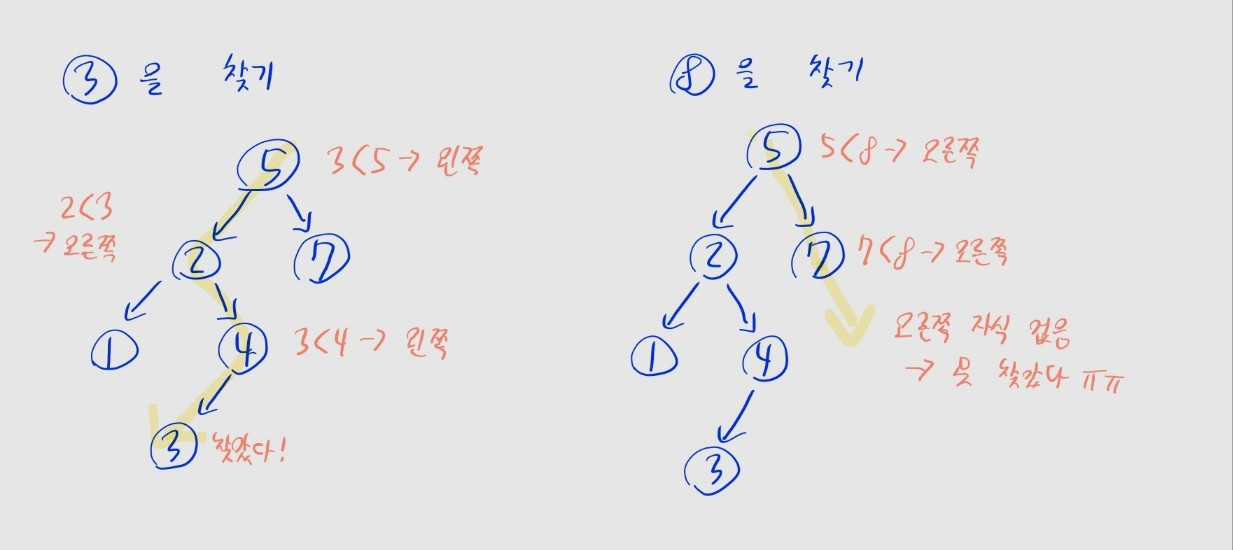
특정 값의 노드 찾기

• 루트 노드부터 노드를 탐색하며, 찾는 값과 비교
  • 찾는 값 == 노드의 값인 경우, 노드를 찾았으므로 현재 노드를 반환
  • 찾는 값 < 노드의 값인 경우, 왼쪽 자식으로 이동
  • 찾는 값 > 노드의 값인 경우, 오른쪽 자식으로 이동
• 이동한 방향의 자식 노드가 존재하지 않는 경우, 탐색에 실패

BSTNode *findBSTNode(BSTNode *node, int value){
    // 널 포인터 -> 탐색에 실패
    if (node == NULL) return NULL;
    
    if (value < (node -> item)){
        // 찾는 값 < 노드의 값 -> 왼쪽 노드 재귀호출
        return findBSTNode(node -> left, value);
    } else if (value > (node -> item)){
        // 찾는 값 > 노드의 값 -> 오른쪽 노드 재귀호출
        return findBSTNode(node -> right, value);
    } else {
        // 노드를 찾았으므로 노드를 반환
        return node;
    }
}

BSTNode *findBST(BST *tree, int value){
    if (tree == NULL) return NULL;
    return findBSTNode(tree -> root, value);
}

• findBSTNode로 각 노드를 재귀적으로 탐색
• 현재 노드의 값 node -> item을 찾는 값 value와 비교
  • value < (node -> item)인 경우, 왼쪽 자식 (node -> left) 탐색
  • value > (node -> item)인 경우, 오른쪽 자식 (node -> right) 탐색
  • 값을 찾은 경우 node 반환
• 찾는 방향에 노드가 없어 node == NULL인 경우 NULL 반환
• findBST로 트리 전체에서 탐색을 시작
  • findBST는 BSTNode * 포인터 대신 BST * 포인터를 매개변수로 받음
  • 트리의 루트 노드 tree -> root를 findBSTNode()에 넘겨 본격적으로 탐색

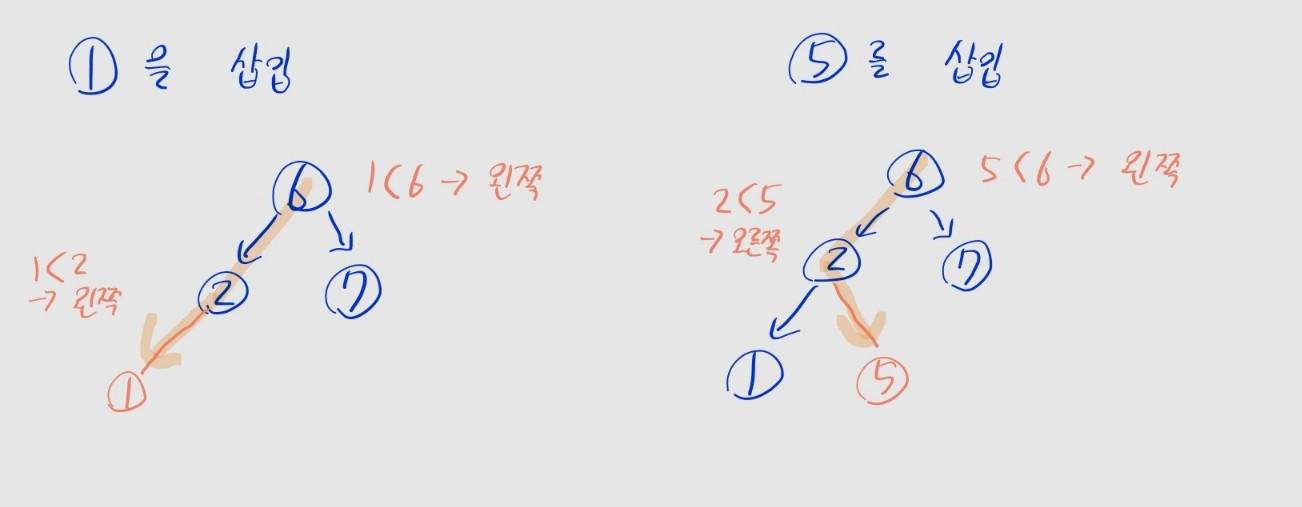
특정 값의 노드 삽입하기

• 특정 값의 노드 찾기와 동일한 방식으로, 삽입할 위치까지 재귀적으로 이동
• 삽입할 빈 위치를 (NULL) 찾은 경우, 새 노드를 생성해 해당 위치에 삽입
• 동일한 값의 노드가 이미 존재할 시, 삽입할 수 없으니 종료

// root가 루트노드인 트리에 값이 value인 노드를 삽입하고, 루트노드를 반환
BSTNode *insertBSTNode(BSTNode *root, int value){

    // 노드를 삽입할 위치까지 이동한 경우
	if (root == NULL){

        // 새로운 노드를 생성
		root = malloc(sizeof(BSTNode));

        // root != NULL을 체크하는 이유: 메모리 할당이 잘 이루어졌는지 확인
		if (root != NULL) {
			// 값은 value, 왼쪽 / 오른쪽 자식은 NULL로 초기화
            root -> item = value;
			root -> left = NULL;
			root -> right = NULL;
		}
	}
	else {
		if (value < (root -> item)){
            // 찾는 값 < 노드의 값 -> 왼쪽 노드 재귀호출
			root -> left = insertBSTNode(root->left, value);
		}
		else if (value > (root -> item)){
            // 찾는 값 > 노드의 값 -> 오른쪽 노드 재귀호출
			root -> right = insertBSTNode(root->right, value);
		}
        else {
            // 찾는 값 == 노드의 값 -> 삽입 불가능, 추가 재귀호출 없음
            printf("이미 동일한 노드가 존재합니다.\n");
        }
    }

    return root; // 노드를 반환
}

void insertBST(BST *tree, int value){
    // insertBSTNode 함수가 반환한 노드를 루트 노드로 설정
    tree -> root = insertBSTNode(tree -> root, value);
}

• insertBSTNode는 root를 루트로 갖는 트리에 값이 value인 노드를 삽입하고, 갱신된 루트 노드를 반환
  • insertBST는 insertBSTNode가 반환한 루트 노드를 tree -> root에 저장
• insertBSTNode의 동작은 재귀적으로 이루어짐
• value < root -> item인 경우 왼쪽 자식으로 이동
  • 왼쪽 자식으로 이동하여 root->left에 대해 insertBSTNode를 재귀 호출
  • 재귀 호출 결과로 반환된 (갱신된) 왼쪽 서브트리의 루트 노드를 root->left에 저장
• value > root -> item인 경우 오른쪽 자식으로 이동
  • 오른쪽 자식으로 이동하여 root->right에 대해 insertBSTNode를 재귀 호출
  • 재귀 호출 결과로 반환된 (갱신된) 오른쪽 서브트리의 루트 노드를 root->right에 저장
• value > root == item인 경우 노드를 삽입할 수 없음
  • 추가 재귀호출 없이, 노드 자기 자신을 반환
• 노드를 삽입할 위치(root == NULL)까지 도달하면, 새로운 노드를 생성하고, 생성된 노드를 반환

특정 값의 노드 제거하기

삭제할 노드까지 탐색

• 결국 노드를 제거하려면, 삭제할 노드의 위치까지 이동해야 함
• 특정 값의 노드 찾기와 동일한 방식으로, 삽입할 노드까지 재귀적으로 이동
• 찾지 못한 경우, 삭제할 수 없으므로 종료

// root가 루트노드인 트리에서 값이 value인 노드를 삭제하고, 루트노드를 반환
BSTNode *removeBSTNode(BSTNode *root, int value){
	// 삭제할 노드를 찾지 못함
	if (root == NULL){
		return root;
	}

	// 삭제할 노드까지 탐색
	if (value < (root -> item)){
		root -> left = removeBSTNode(root -> left, value);
		return root;
	} else if (value > (root -> item)){
		root -> right = removeBSTNode(root -> right, value);
		return root;
	}
    // 이후 코드에서 계속
}

• removeBSTNode는 root를 루트로 갖는 트리에서 값이 value인 노드를 제거하고, 갱신된 루트 노드를 반환
• 재귀적으로 삭제할 노드까지 탐색
  • value < root -> item인 경우 왼쪽 서브트리로 이동하여 root -> left에 대해 재귀 호출 -> 반환(갱신)된 노드를 root->left에 저장
  • value > root -> item인 경우 오른쪽 서브트리로 이동하여 root -> right에 대해 재귀 호출 -> 반환(갱신)된 노드를 root->right에 저장
• 삭제할 노드를 찾지 못한 경우, 추가 재귀 호출 없이 노드 자기 자신을 반환
• 삭제할 노드를 찾은 경우, 즉 value == (root -> item)인 경우
  • 위 세 조건문 중 아무것도 충족하지 않아, 하단의 코드로 넘어가 삭제가 진행됨

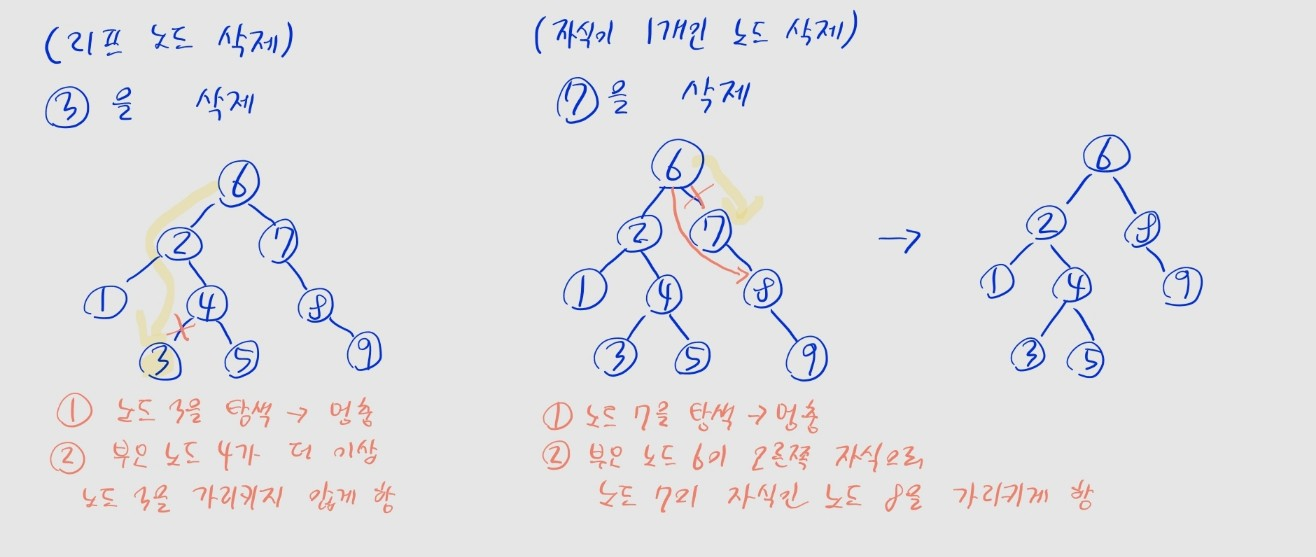
삭제할 노드가 리프 노드인 경우

BSTNode *removeBSTNode(BSTNode *root, int value){
    // 이전 코드에서 계속
	if (root -> left == NULL && root -> right == NULL){
		// (1) 내가 리프 노드일 때 -> 나만 사라지면 그만이야.
		free(root);
		return NULL;
	}
    // 이후 코드에서 계속
}

• 단순히 부모 노드가 가리키는 자식을 제거하면 됨
• free로 삭제할 노드 root의 메모리 할당을 해제
• 이후 NULL을 반환해, 부모 노드가 자식을 가리키지 않도록 업데이트

삭제할 노드의 자식이 1개인 경우

BSTNode *removeBSTNode(BSTNode *root, int value){
    // 이전 코드에서 계속
    else if (root -> left == NULL){
		// (2) 오른쪽 자식만 있을 때 -> 오른쪽 자식에게 넘겨주자.
		BSTNode *newNode = root -> right;
		free(root);
		return newNode;
	} else if (root -> right == NULL){
		// (2) 왼쪽 자식만 있을 때 -> 왼쪽 자식에게 넘겨주자.
		BSTNode *newNode = root -> left;
		free(root);
		return newNode;
	}
    // 이후 코드에서 계속
}

• 부모 노드가 삭제할 노드의 자식을 가리키도록 업데이트해야 함
• newNode에 자식 (root -> left / root -> right)을 저장하고,
• free로 삭제할 노드 root의 메모리 할당을 해제하고,
• newNode를 반환해, 부모 노드가 삭제한 노드의 자식일 가리키도록 업데이트

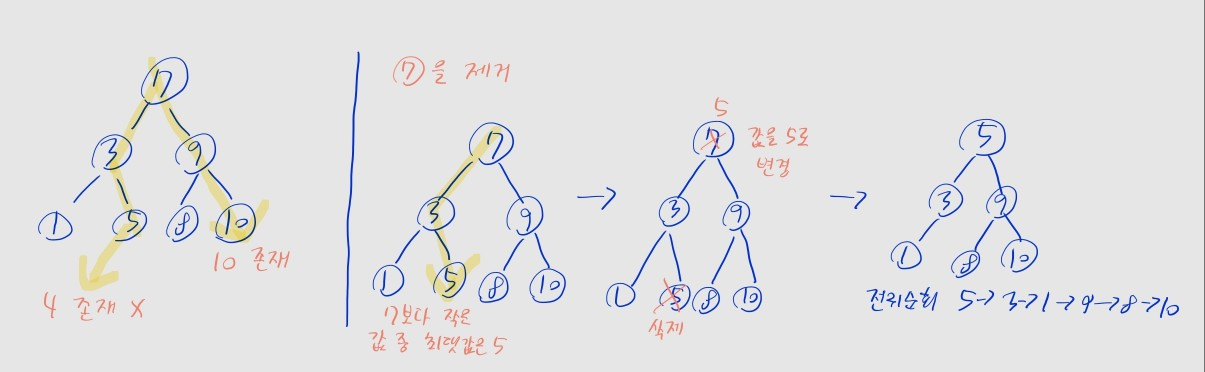
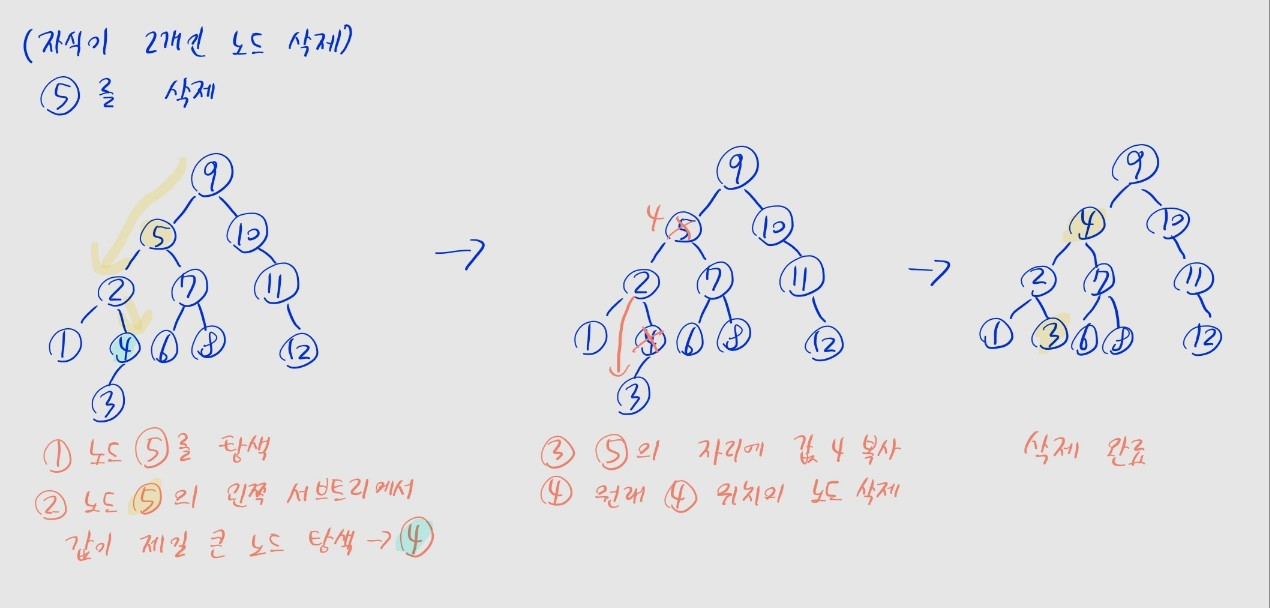
삭제할 노드의 자식이 2개인 경우

BSTNode *removeBSTNode(BSTNode *root, int value){
    // 이전 코드에서 계속
    else{
		// (3) 두 자식이 둘 다 있을 때
		// (3a) 삭제할 트리의 왼쪽 서브트리에서 최댓값 노드를 찾는다.
		// 그니까 처음엔 왼쪽으로 가고, 
		BSTNode *maxNode = root -> left;
        // 다음엔 계속 오른쪽으로 간다.
		while (maxNode -> right != NULL){
			maxNode = maxNode -> right;
		}
		// (3b) 루트의 값을 바꾼다.
		root -> item = maxNode -> item;

		// (3c) 검색한 위치의 노드를 삭제한다.
		root -> left = removeBSTNode(root -> left, maxNode -> item);
		return root;
	}
}

• (a) 삭제할 노드의 왼쪽 서브트리에서 최댓값 노드를 검색 (이를 maxNode 변수로 둠)
  • 말이 어려운데, 삭제할 노드보다 작은 값 중 최댓값을 찾는 과정임
  • 첫 번째만 왼쪽으로 이동
  • 다음엔 오른쪽 자식이 없을 때까지 계속 오른쪽으로 이동하면 됨
• (b) 삭제할 노드 위치의 값을, maxNode의 값으로 변경
• (c) maxNode 위치의 노드를 삭제
  • 해당 노드가 리프면, 리프 노드일 때와 같이 삭제
  • 해당 노드가 자식이 1개라면, 자식이 1개인 노드일 때와 같이 삭제
  • 이건 removeBSTNode를 다시 호출해 주면 알아서 해 줌
• 이후 root 반환

최종 처리

void removeBST(BST *tree, int value){
    tree -> root = removeBSTNode(tree -> root, value);
}

• removeBST는 removeBSTNode가 반환한 루트 노드를 tree -> root에 저장

전위, 중위, 후위 순회

• 전위 순회: (자기 자신 방문) -> (왼쪽 자식 탐색) -> (오른쪽 자식 탐색)
• 중위 순회: (왼쪽 자식 탐색) -> (자기 자신 방문) -> (오른쪽 자식 탐색)
• 후위 순회: (왼쪽 자식 탐색) -> (오른쪽 자식 탐색) -> (자기 자신 방문)

void preOrder(BSTNode *root)
{
    // NULL일 땐 바로 return (종료조건)
	if (root == NULL) return;

	printf("%d ", root -> item);    // 자기 자신 방문
	preOrder(root -> left);         // 왼쪽 자식 탐색
	preOrder(root -> right);        // 오른쪽 자식 탐색
}

void inOrder(BSTNode *root)
{
	// NULL일 땐 바로 return (종료조건)
	if (root == NULL) return;

	inOrder(root -> left);          // 왼쪽 자식 탐색
	printf("%d ", root -> item);    // 자기 자신 방문
	inOrder(root -> right);         // 오른쪽 자식 탐색
}

void postOrder(BSTNode *root)
{
    // NULL일 땐 바로 return (종료조건)
	if (root == NULL) return;

	postOrder(root -> left);        // 왼쪽 자식 탐색
	postOrder(root -> right);       // 오른쪽 자식 탐색
	printf("%d ", root -> item);    // 자기 자신 방문
}

• 노드를 방문할 땐 root -> item(노드의 값) 출력
• 왼쪽 / 오른쪽 노드로 이동할 땐 동일 함수를 재귀 호출
• root == NULL일 때 재귀호출 없이 종료

메모리 할당 해제

void removeAll(BSTNode *node)
{
	if (node != NULL)
	{
		removeAll(node -> left);
		removeAll(node -> right);
		free(node);

	}
}

• malloc을 했으므로 free 해주는 건 이제 기본이지?
• 후위 순회와 유사하게, 왼쪽 / 오른쪽 노드에 대해 재귀 호출을 우선 진행
• 재귀 호출 이후, node 자기 자신의 메모리 할당 해제

동작과정

int main(void){
	BST bs_tree;
	bs_tree.root = NULL;

	int nums[7] = {7, 3, 9, 1, 5, 8, 10};

	// 값을 삽입
	for (int i = 0; i < 7; i++){
		insertBST(&bs_tree, nums[i]);
	}

	// 전위 순회
	preOrder(bs_tree.root);		// 7 3 1 5 9 8 10 
	printf("\n");
	
	// 중위 순회
	inOrder(bs_tree.root);		// 1 3 5 7 8 9 10 
	printf("\n");

	// 후위 순회
	postOrder(bs_tree.root);	//1 5 3 8 10 9 7 
	printf("\n");
    
    // 이후 코드에서 계속
}

int main(void){
	// 이전 코드에서 계속

	// 노드 탐색
	BSTNode *found = findBST(&bs_tree, 10);
	if (found != NULL){
		printf("노드 10을 찾았습니다.\n");
	} else {
		printf("노드 10을 찾지 못했습니다.\n");
	}
	// 노드 10을 찾았습니다.

	found = findBST(&bs_tree, 4);
	if (found != NULL){
		printf("노드 4를 찾았습니다.\n");
	} else {
		printf("노드 4를 찾지 못했습니다.\n");
	}
	// 노드 4를 찾지 못했습니다.

	// 노드 삭제
	removeBST(&bs_tree, 7);
	preOrder(bs_tree.root);	// 5 3 1 9 8 10
	// 5가 새로운 루트노드가 되었음에 유의
    
    // 메모리할당해제 및 모두 삭제
	removeAll(bs_tree.root);
    bs_tree.root = NULL;
}