[PS] 동적 계획법 (DP)

방법이있지·2025년 6월 5일

Problem Solving 크래프톤 정글

[정글 1-4주차] Problem Solving

목록 보기

24/26

~~DP가 이 DP는 아니겠죠...? ㅎㅎㅎㅎㅎ~~

흔히 Dynamic Programming(DP)라고도 부르는 동적 계획법은, 중복되는 하위 문제로 쪼갤 수 있는 문제를 해결할 때 활용합니다.

동적 계획법

전체 문제를 하위 부분 문제로 나누어 해결하는 방법
- 이미 계산된 하위 문제의 해답은 별도의 메모리에 저장
- 같은 문제를 반복 계산하지 않으므로, 수행 시간이 빨라짐
문제가 다음 두 조건을 만족해야 사용할 수 있음
- 중복되는 부분 문제: 동일한 부분 문제를 반복적으로 해결해야 함
- 최적 부분 구조: 문제를 부분 문제로 나눌 수 있으며, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있음

🤔 분할 정복에서도 큰 문제를 부분 문제로 분할하지 않았나요?

맞습니다. 하지만 분할 정복은 동적 계획법과 달리, 동일한 부분 문제를 반복적으로 해결할 필요가 없습니다.
예를 들어, 분할 정복의 대표적 예시인 병합 정렬의 경우 배열을 서로 다른 두 부분배열로 나누어 정렬한 뒤 다시 합칩니다.
이때 나눈 두 부분 배열은 중복되지 않기 때문에, 동일한 부분 문제로 볼 수 없습니다.

피보나치 수열

$1, 1, 2, 3, 5, 8, 13, 21, 34, 55...$

와 같은 형태의 수열
피보나치 수열의 $i$ 번째 항을 $a_i$ 로 둘 때 (단, $i \geq 1$ )
- $a_n = a_{n-1} + a_{n-2}, a_1 = 1, a_2 = 1$ 의 점화식을 따름
- 대충 앞선 두 항의 값을 더하면, 현재 항의 값이 된다는 뜻
이러한 점화식은 재귀함수로 구현할 수 있음

피보나치 수열 함수 구현

# 피보나치수열의 x번째 값 (단, x는 1부터 시작)
def fibo(x):
    if x == 1 or x == 2:
        return 1
    return fibo(x - 1) + fibo(x - 2)

print(fibo(6))  # 8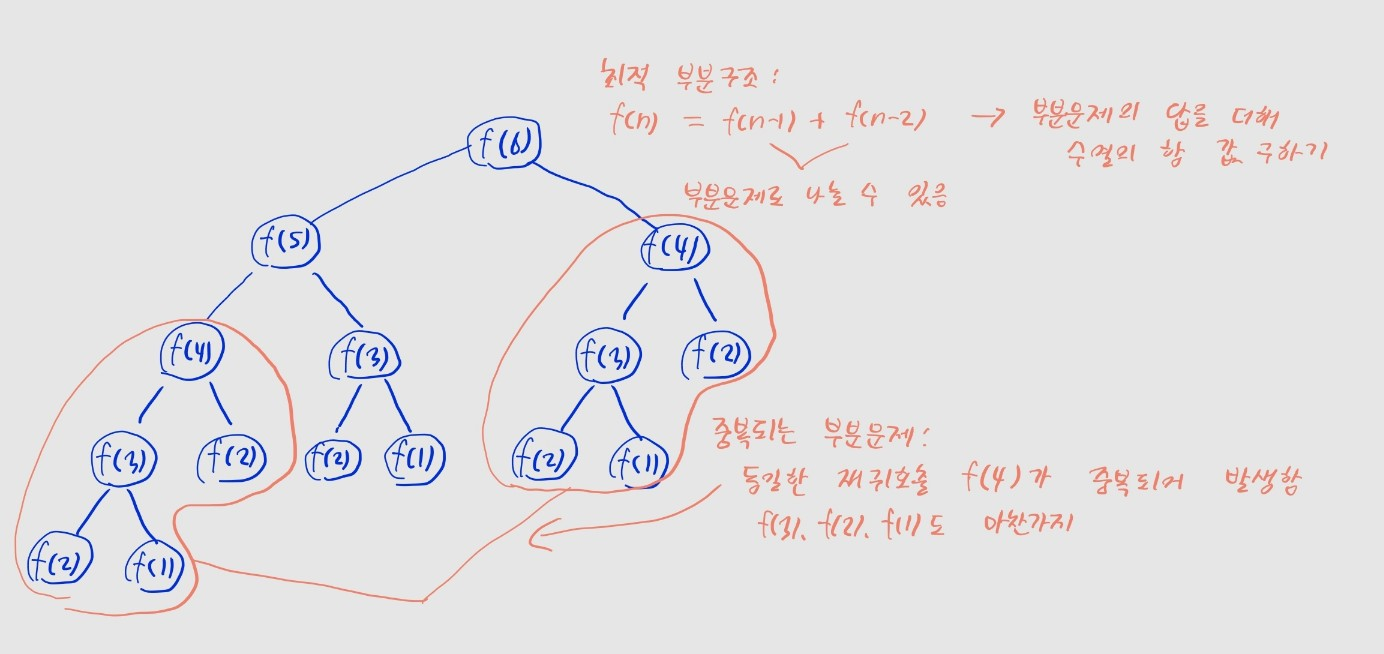

이 함수에서 최적 부분 구조를 확인할 수 있음
- 큰 문제 fibo(6)를 작은 문제 fibo(5)와 fibo(4)로 나누고
- 두 결과를 더해서 더 큰 문제인 fibo(6)를 해결할 수 있음
실제 함수 호출 시, 동일 함수가 여러 번 호출됨 -> 중복되는 부분 문제
- fibo(6)을 계산하는 과정에서 fibo(4)가 반복적으로 호출됨
- fibo(3), fibo(2), fibo(1)도 마찬가지
- 이때 각 함수의 반환값을 별도 메모리에 저장...즉 메모해 두면, 중복 계산을 줄여 실행 시간을 단축할 수 있음 -> 메모이제이션

메모이제이션

한 번 계산한 결과를 별도 메모리 공간에 저장하는 기법
- 파이썬에서는 보통 리스트에 계산 결과를 저장
- 이러한 리스트를 DP 테이블이라고도 부름
동일 문제가 다시 호출되면, 저장한 결과를 바로 가져옴

🐥 일부 책이나 강의에선 상향식 방식만을 동적 계획법, 하향식 방식만을 메모이제이션이라고 엄격하게 구분하기도 합니다...만

어차피 상향식이든 하향식이든 이미 계산한 결과를 메모해서 재활용한다는 점에선 본질적으로 같기에, 이 글에선 굳이 구분하지 않겠습니다.
실제 코딩테스트에서는 동적계획법 = 메모이제이션 이라고 여겨지기도 하고요.

하향식 방식

큰 문제를 해결하기 위해, 작은 문제를 재귀적으로 호출
- 재귀호출을 사용하며, 함수의 반환 결과를 DP 테이블에 저장해 중복 계산을 방지

# memo[i]에 fibo(i)의 반환값을 저장
# 아직 계산하지 못한 경우 None
memo = [None] * 100

# 피보나치수열의 i번째 값 (단, x는 1부터 시작)
def fibo(i):
    # 첫번째, 두번째 값은 1
    if i == 1 or i == 2:
        return 1
    if memo[i] is not None:     # 이미 계산한 적 있는 경우
        return memo[i]
    # 아직 계산하지 않은 경우, 계산 후 결과를 memo 리스트에 저장
    memo[i] = fibo(i - 1) + fibo(i - 2)
    return memo[i]

print(fibo(99)) # 218922995834555169026

이젠에 결과를 구한 함수가 호출될 시, 바로 memo 리스트(DP 테이블)에 저장한 결과를 가져와서 시간이 단축됨
- fibo(6)을 구할 때, 아래 그림에서 노란색으로 칠한 함수만 실제로 호출됨

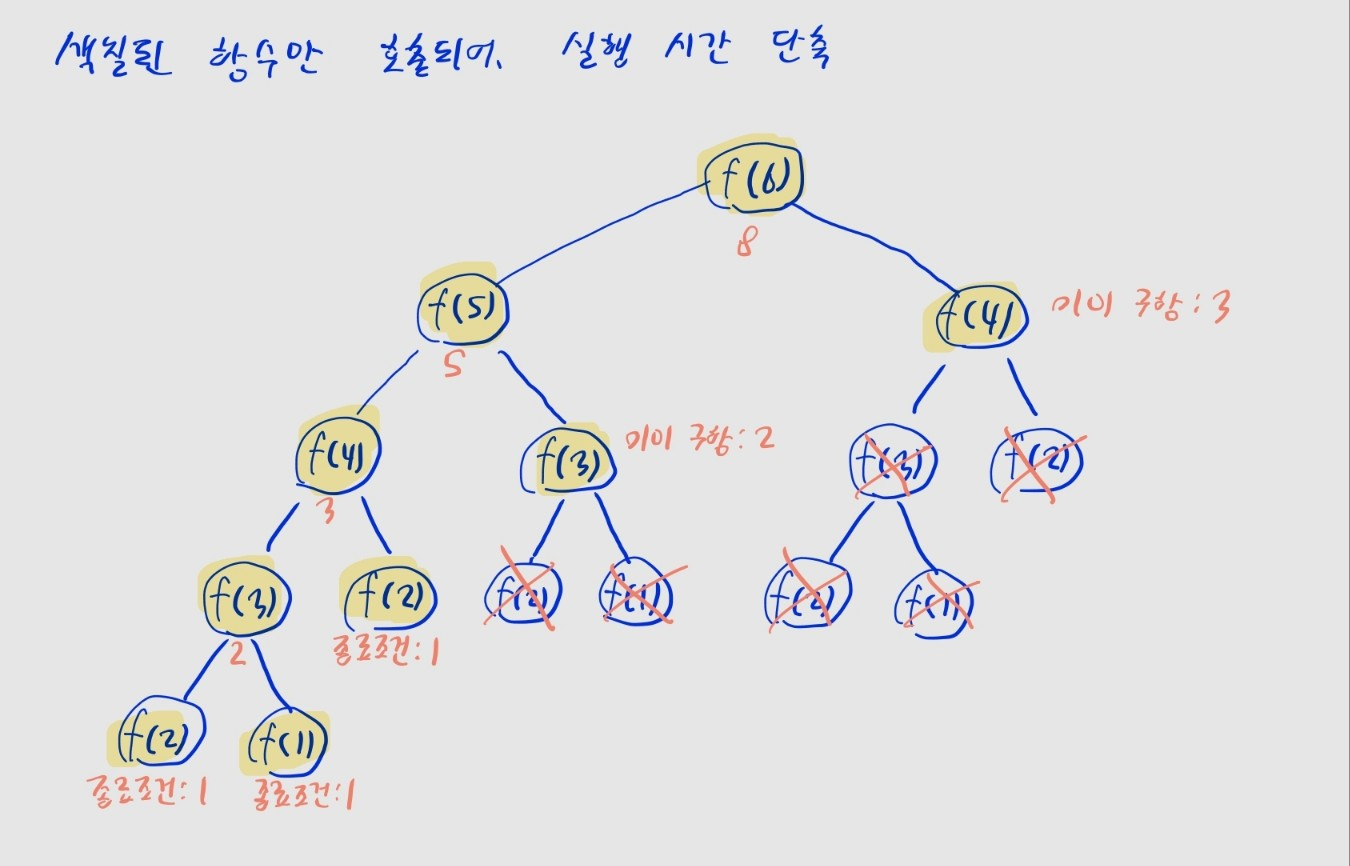
상향식 방식

작은 문제부터 차례대로 해결하면서, 큰 문제로 확장
- 반복문을 사용하며, 이전에 계산한 결과를 DP 테이블에 저장하고, 이를 이용해 다음 결과를 계산

# memo[i]는 피보나치수열의 i번째 값 (단 i는 1부터 시작)
# 아직 계산하지 못한 경우 None
memo = [None] * 100

# memo[i]는 피보나치수열의 i번째 값
for i in range(1, 100):
    # 첫번째, 두번째 값은 1
    if i == 1 or i == 2:
        memo[i] = 1
    else:
        memo[i] = memo[i - 1] + memo[i - 2]

print(memo[99]) # 218922995834555169026

fibo(6)을 구할 때, 수열 이전 항의 값은 1번씩만 계산됨
이때 계산된 값을 이후 계산에 활용

x memo[x]
1 1
2 1
3 memo[2] + memo[1] = 2
4 memo[3] + memo[2] = 3
5 memo[4] + memo[3] = 5
6 memo[5] + memo[4] = 8

`x`	`memo[x]`
`1`	`1`
`2`	`1`
`3`	`memo[2] + memo[1] = 2`
`4`	`memo[3] + memo[2] = 3`
`5`	`memo[4] + memo[3] = 5`
`6`	`memo[5] + memo[4] = 8`

🤔 **왜 두 코드에서 굳이 if i == 1 or i == 2 를 따로 조건문 처리 해 주나요? 그냥 memo[1] = 1, memo[2] = 1로 미리 저장하고 반복문 / 재귀호출을 하면 되는 거 아니에요?

일반적으로 피보나치 수열의 N번째 수를 구할 때, memo 리스트는 N + 1의 길이로 만듭니다.
가끔씩 백준에서 피보나치 수열의 1번째 수를 물을 때가 있습니다. 그러면 memo는 0과 1 인덱스만 갖는 길이 2의 리스트가 됩니다.
그러면 memo[2]가 존재하지 않아서 memo[2] = 1로 대입하려고 하면 IndexError가 뜹니다. 예외 처리라고 생각해주시면 됩니다.

시간 복잡도

피보나치수열의 $N$ 번째 수를 구할 때, 상향식, 하향식 방식 모두 피보나치 수열의 첫 값부터 $N$ 번째까지의 값을 1번씩 계산함
따라서 $O(N)$

🤔 시간 복잡도도 동일한데, 그래서 뭘 써야 해요?

뭘 쓰든 상관없긴 합니다. 점화식을 그대로 옮겨오면 되는 하향식이 직관적이긴 합니다.
대신 하향식을 사용할 땐 재귀 깊이 제한을 sys.setrecursionlimit(10**9)으로 높여줄 필요가 있음을 고려하세요. 그리고 가끔씩 재귀로는 시간제한 뜨는 문제들이 있어서, 재귀 필요없는 상향식을 선호하긴 합니다.
또한 때로는 문제를 어떻게 쪼개야 할지 점화식을 생각하기도 어려운 문제도 나오는데요, 이럴 땐 상향식으로 어떻게든 작은 문제부터 합치다 보면 답이 나오는 경우도 있습니다. (아래의 '동전 2' 문제 참고)

문제풀이

2748. 피보나치 수 2

백준 / 브론즈 1 / 2748. 피보나치 수 2

이 문제는 글에서 설명한 거랑 살짝 다르게 0번째 수를 0, 1번째 수를 1로 두고 더해 나가는데... 핵심 원리는 같습니다 뭐
시간 복잡도는 역시 $O(N)$

N = int(input())
memo = [None] * (N + 1)

def fibo(x):
    if x == 0:
        return 0
    elif x == 1:
        return 1
    if memo[x] is not None:
        return memo[x]
    memo[x] = fibo(x - 1) + fibo(x - 2)
    return memo[x]

print(fibo(N))