
자료구조 알고리즘 주차는 오늘이 마지막이고 내일부터는 C언어로 본격적으로 넘어가게 됩니다.
그래서 작별인사 느낌으로 지금까지 공부한 내용들을 한 글로 정리해보았습니다.
1주차
파이썬 문제풀이 유의점 ⭐⭐
연속된 숫자가 나타났다?
map으로 각 원소에int적용
# `12345`와 같이 공백 없는 숫자 입력
a, b, c, d, e = map(int, input()) # 각각 변수로
nums = list(map(int, input())) # 리스트로
# `1 2 3 4 5`와 같이, 공백으로 구분된 숫자 입력
a, b, c, d, e = map(int, input().split()) # 각각 변수로
nums = list(map(int, input().split())) # 리스트로입력 데이터가 많다?
sys.stdin.readline으로 빠르게 입력 받기- 대신 입력에 개행 문자
\n을 포함하므로, 수동으로 없애줘야 함
- 대신 입력에 개행 문자
import sys
input = sys.stdin.readline
text = input().strip() # 맨 뒤 '\n'을 제거
num = int(input()) # int 등 함수는 자동 제거재귀 문제다?
- DFS, 분할 정복, 이분 탐색, 백트래킹, DP 하향식 접근...
- 무조건 무조건 무조건, 더 이상 재귀 호출을 하지 않는 종료 조건을 둘 것. 안 두면 무한 재귀 발생.
sys.setrecursionlimit(최대깊이)로 최대 재귀 깊이를 늘려 스택 오버플로우 방지- 기본값은
10 ** 3인데, 보통10 ** 9정도로 늘리면 문제없음
- 기본값은
import sys
sys.setrecursionlimit(10 ** 9)
# 유클리드 호제법
def gcd(x, y):
if y == 0: # 무조건 종료 조건을 둘 것
return x
else:
return gcd(y, x % y)
print(gcd(22, 8)) # 2시간 복잡도 ⭐⭐
- 문제를 꼼꼼히 읽어서 의 크기를 파악하고, 적절한 시간 복잡도를 파악하는 건 기본이지
- 아래 표는 1초 시간제한 기준, 입력의 크기에 따른 가능한 최대 시간 복잡도
| N 크기 | 가능한 최대 시간 복잡도 | 예시 |
|---|---|---|
| 약 | 조합, 순열 등 | |
| 약 | 완전 탐색 등 | |
| 약 | 삼중 반복문 | |
| 약 | 이중 반복문 | |
| 약 ~ | 정렬 | |
| 약 ~ | 단일 반복문, 선형 탐색 | |
| 사실상 무한 | 이분 탐색 | |
| 무한 | 수학공식 등 신박한 풀이 |
배열 ⭐
- 파이썬 리스트를 사용해 구현
- 2차원 배열은
[[0] * (열의 수) for _ in range(행의 수)]로 쉽게 만들 수 있음
| 연산 | 코드 | 시간복잡도 |
|---|---|---|
| 인덱스로 원소 접근 | list[인덱스] | |
| 맨 뒤에 값을 삽입 | list.append(값) | |
| 맨 뒤의 값을 삭제 | list.pop() -> 매개변수 없으면 마지막 인덱스 삭제 | |
| 원소 수 확인 | len(list) | |
| 맨 앞 / 중간에 값을 삽입 | list.insert(인덱스, 값) | |
| 맨 앞 / 중간의 값 삭제 | list.pop(인덱스) | |
| 원소의 존재 여부 확인 | 값 (not) in list | |
| 슬라이싱 | list[a:b] | 는 슬라이싱된 원소 수 |
| 그 외... | list.index(값), list.count(값) |
- 맨 앞 값 건드려야 하면 리스트 말고 데크(
deque) 쓸 것.deque.appendleft()로 추가,deque.popleft()로 삭제는
- 특정 값의 존재 여부를 확인해야 하면 집합 (
set) 쓸 것.- 집합의 경우
in,not in연산은
- 집합의 경우
정렬 알고리즘 ⭐
- 파이썬
.sort(),sorted()의 시간 복잡도는 약
words = ['banana', 'melon', 'kiwi', 'pineapple', "grape"]
print(sorted(words))
# ['banana', 'grape', 'kiwi', 'melon', 'pineapple']
print(sorted(words, reverse=True)) # 내림차순 정렬
# ['pineapple', 'melon', 'kiwi', 'grape', 'banana']
print(sorted(words, key=lambda x: (len(x), x)))
# 길이 순 -> 길이가 같으면 사전 순으로 정렬
# ['kiwi', 'grape', 'melon', 'banana', 'pineapple']순열과 조합 ⭐
- 가능한 경우의 수를 구하는 문제일 시,
itertools를 이용해 순열, 조합 계산 가능 - DFS 백트래킹을 이용한 재귀로도 풀 수 있긴 함
조합
- 순서를 고려하지 않고 뽑음 (e.g.,
(1, 2),(2, 1)은 같은 조합) - 원소가 개인 객체에서 개를 뽑을 때, 총 번 계산
from itertools import combinations
a = [1, 2, 3, 4]
# 리스트 a에서 원소 2개를 뽑은 조합을 튜플로 반환
for cmb in combinations(a, 2):
print(cmb, end=" ")
# (1, 2) (1, 3) (1, 4) (2, 3) (2, 4) (3, 4)순열
- 순서를 고려하고 뽑음 (e.g.,
(1, 2),(2, 1)은 다른 순열) - 원소가 개인 객체에서 개를 뽑을 때, 총 번 계산
from itertools import permutations
a = [1, 2, 3, 4]
# 리스트 a에서 원소 2개를 뽑은 순열을 튜플로 반환
for pm in permutations(a, 2):
print(pm, end=" ")
# (1, 2) (1, 3) (1, 4) (2, 1) (2, 3) (2, 4) (3, 1) (3, 2) (3, 4) (4, 1) (4, 2) (4, 3)2주차
스택 ⭐
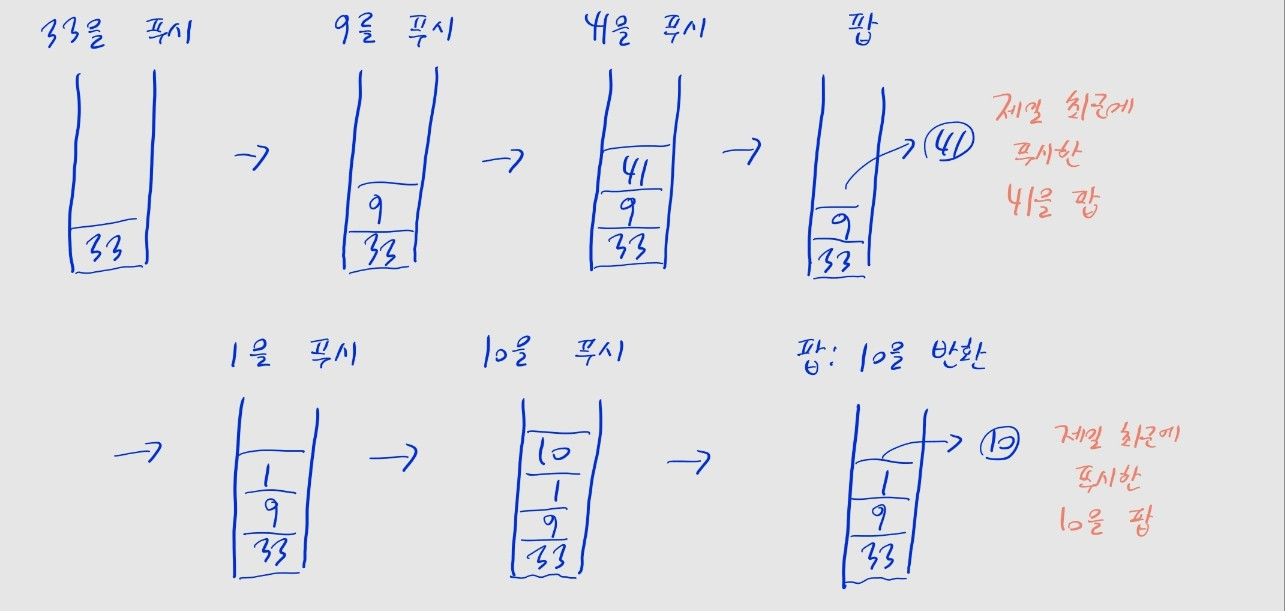
- 후입선출 (Last In First Out) 자료구조
- 가장 나중에 삽입(push)한 데이터를 먼저 꺼냄(pop)
- 파이썬
list.append()로 푸시,list.pop()으로 팝,list[-1]로 맨 위 원소 확인 가능- 모두 시간 복잡도
stack = []
# 스택에 데이터 푸시: .append()
stack.append(33)
stack.append(9)
stack.append(41)
# 스택에서 데이터 팝: .pop()
# 빈 스택에서 팝할 시, IndexError 발생하니 유의할 것
print(stack.pop()) # 41
# 다시 데이터 푸시
stack.append(1)
stack.append(10)
# 스택의 마지막 값 확인
print(stack[-1]) # 10
# 스택의 크기 구하기
stack_size = len(stack) # 현재 스택은 [33, 9, 1, 10]
print(stack_size) # 4
# 다시 데이터 팝
print(stack.pop()) # 10큐 ⭐⭐
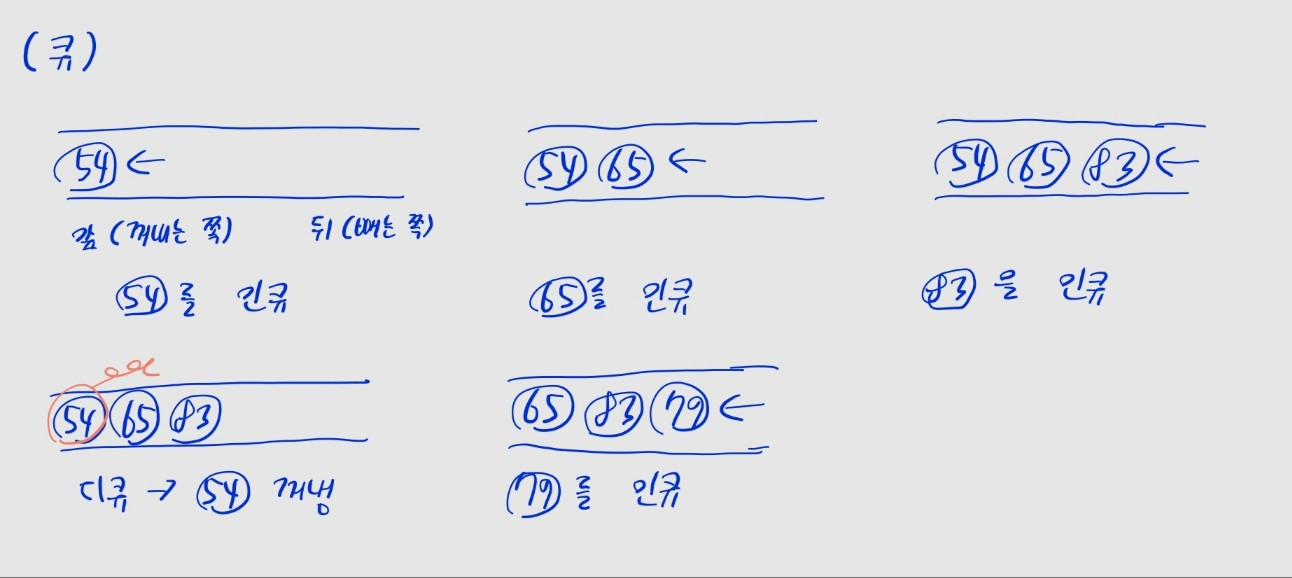
- 선입선출 (First In First Out) 자료구조
- 가장 먼저 삽입(enqueue)한 데이터를 먼저 꺼냄(dequeue)
- 파이썬
collections.deque(데크)로 구현deque.append()로 인큐,deque.popleft()로 디큐,deque[0]로 맨 앞 원소 확인 가능- 모두 시간 복잡도
- BFS, 위상 정렬 등 구현에 사용됨
from collections import deque
queue = deque()
# 큐에 데이터 인큐: .append()
queue.append(33)
queue.append(9)
queue.append(41)
# 큐에서 데이터 디큐: .popleft()
print(queue.popleft()) # 33
# 다시 데이터 인큐
queue.append(1)
queue.append(10)
# 큐의 맨 앞 값 확인
print(queue[0]) # 9
# 큐의 크기 구하기
queue_size = len(queue) # 현재 큐는 [9, 41, 1, 10]
print(queue_size) # 4
# 다시 데이터 디큐
print(queue.popleft()) # 9해시 테이블 ⭐⭐
- 파이썬의 집합, 딕셔너리는 해시 테이블 기반
- 따라서 값의 탐색, 삽입, 삭제가 에 근접
딕셔너리
- 키, 값이 함께 저장된 해시테이블
- 키는 중복될 수 없고, 값은 중복될 수 없음
- e.g.,
players = {51: "창기", 10: "지환", 1: "찬규"}- 데이터 접근 (
a[51]): 에 근접 - 데이터 삽입, 수정 (
a[8] = "성주"): 에 근접 - 데이터 삭제 (
a.pop(10)): 에 근접
- 데이터 접근 (
- 해시 테이블엔 순서가 없지만,
dict는 삽입 순서를 유지하도록 구현됨for key in dict등 사용 시, 정해진 순서대로 순회
집합
- 키만 저장된 해시테이블
- 키는 중복값을 허용하지 않으므로, 집합 역시 중복된 값을 저장할 수 없음
- e.g.,
nums = {1, 2, 3}- 원소 존재여부 확인 (
1 in a): 에 근접 - 원소 삽입 (
nums.add(4)): 에 근접 - 원소 삭제 (
nums.remove(3)): 에 근접
- 원소 존재여부 확인 (
- 집합에는 순서가 없어,
for num in nums등 사용 시 임의의 순서대로 순회됨
Counter - 개수 세기
- 문자열, 리스트 등 이터러블 객체의 원소 개수를 세는 데 특화된 딕셔너리
- 키: 원소, 값: 해당 원소의 개수
from collections import Counter
a = Counter("123456654456")
print(a)
# Counter({'4': 3, '5': 3, '6': 3, '1': 1, '2': 1, '3': 1})
# 없는 키를 인덱싱할 시, KeyError 발생 X - 0을 리턴
print(a['4']) # 3
print(a['2']) # 1
print(a['0']) # 없는 키: 0
print(a['ㄹㅇㄹㅇㄹㅇ']) # 없는 키: 0
# 가장 많이 등장한 항목 순으로, (원소, 개수) 쌍 확인
print(a.most_common())
# [('4', 3), ('5', 3), ('6', 3), ('1', 1), ('2', 1), ('3', 1)]
print(a.most_common(2)) # 상위 2개만
# [('4', 3), ('5', 3)]defaultdict - 기본값 부여
- 딕셔너리에 기본값을 지정할 수 있음
- 없는 키에 접근해도,
KeyError발생 X - 대신 자동으로 해당 키에 기본값을 할당
defaultdict(int)의 기본값은 0,defaultdict(list)의 기본값은[]defaultdict(lambda: '기본값')으로 원하는 기본값 설정 가능
- 없는 키에 접근해도,
from collections import defaultdict
# 기본값이 0
count = defaultdict(int)
count["딸기"] += 1 # 기본값인 0에 1 더함
print(count) # defaultdict(<class 'int'>, {'딸기': 1})
# 기본값이 빈 리스트
songs = defaultdict(list)
songs["이찬혁"].append("이찬혁") # 기본값인 빈 리스트에 원소 삽입
songs["악뮤"].append("이수현")
print(songs) # defaultdict(<class 'list'>, {'악뮤': ['이찬혁', '이수현']})
# 사용자 정의 기본값
points = defaultdict(lambda: 50)
print(points["상록"]) # 기본값인 50 반환
print(points) # defaultdict(<function <lambda> at 0x00000201556E9760>, {'상록': 50})최소 / 최대 힙 ⭐⭐

왜 여기만 그래픽이 깔쌈하냐고요? 정글 책만들기 과제에서 제가 맡은 부분이 여기여서...
- 완전 이진 트리의 일종
- 단, 부모의 값이 항상 자식보다 작거나 같음 (최소 힙)
- 단, 부모의 값이 항상 자식보다 크거나 같음 (최대 힙)
- 원소의 삽입, 삭제가 발생할 때마다 최솟값, 최댓값이 루트에 오도록 원소가 자동으로 재배치됨
- 매번 최솟값 or 최댓값을 꺼낼 수 있는 우선순위 큐 구현에 사용
- 파이썬의
heapq모듈 사용해, 리스트를 최소 힙처럼 사용 가능heapq.heappush(리스트, x)로 삽입 ()heapq.heappop(리스트)로 최솟값 꺼내기 ()리스트[0]으로 현재 루트 노드의 최솟값 확인 ()heapq.heapify(리스트)로 기존 리스트의 원소를 힙 조건을 만족하도록 재배치 가능 ()
import heapq
heap = []
# 힙에 값 삽입
heapq.heappush(heap, 3)
heapq.heappush(heap, 1)
heapq.heappush(heap, 5)
# 현재 최솟값 확인 (루트노드)
print(heap[0]) # 1
# 힙에서 값 꺼내기
print(heapq.heappop(heap)) # 1
print(heapq.heappop(heap)) # 3
print(heapq.heappop(heap)) # 5
# 기존 리스트를 최소 힙으로 재구성
b = [9, 5, 2, 7]
heapq.heapify(b)
print(b[0]) # 2
print(heapq.heappop(b)) # 2heapq는 최소 힙 기반이므로, 최대 힙처럼 사용할 땐 값을 음수 처리해 주어야 함

이분 탐색 ⭐⭐
- 배열에서 원하는 값의 인덱스를 찾는 알고리즘
- 선형 탐색: 배열의 값을 하나씩 확인하며 찾는 값과 일치하는지 확인, 소요
list.index(x)메서드도 선형 탐색,

- 이분 탐색: 이미 정렬된 배열에서, 만에 값을 탐색할 수 있는 방법
- 매번 배열 중앙의 원소와 찾는 값을 비교
- 중앙의 원소값 < 찾는 값: 탐색 범위를 중앙 인덱스 이후로 좁힘
- 중앙의 원소값 > 찾는 값: 탐색 범위를 중앙 인덱스 이전으로 좁힘
- 값을 찾거나, 더 탐색할 범위가 없을 때까지 반복
# a에서 target 찾기
def binary_search(a, target):
l = 0 # 검색 범위 맨 앞의 인덱스
r = len(a) - 1 # 검색 범위 맨 끝의 인덱스
while True:
m = (l + r) // 2 # 중앙 원소의 인덱스
if a[m] == target: # target을 찾은 경우
return m
elif a[m] < target: # 인덱스 m 이후에 target 존재
l = m + 1
else:
r = m - 1
if l > r: # 더 이상 검색할 값이 없음
return -1 # 찾지 못한 경우 -1 반환
print()분할 정복 ⭐⭐
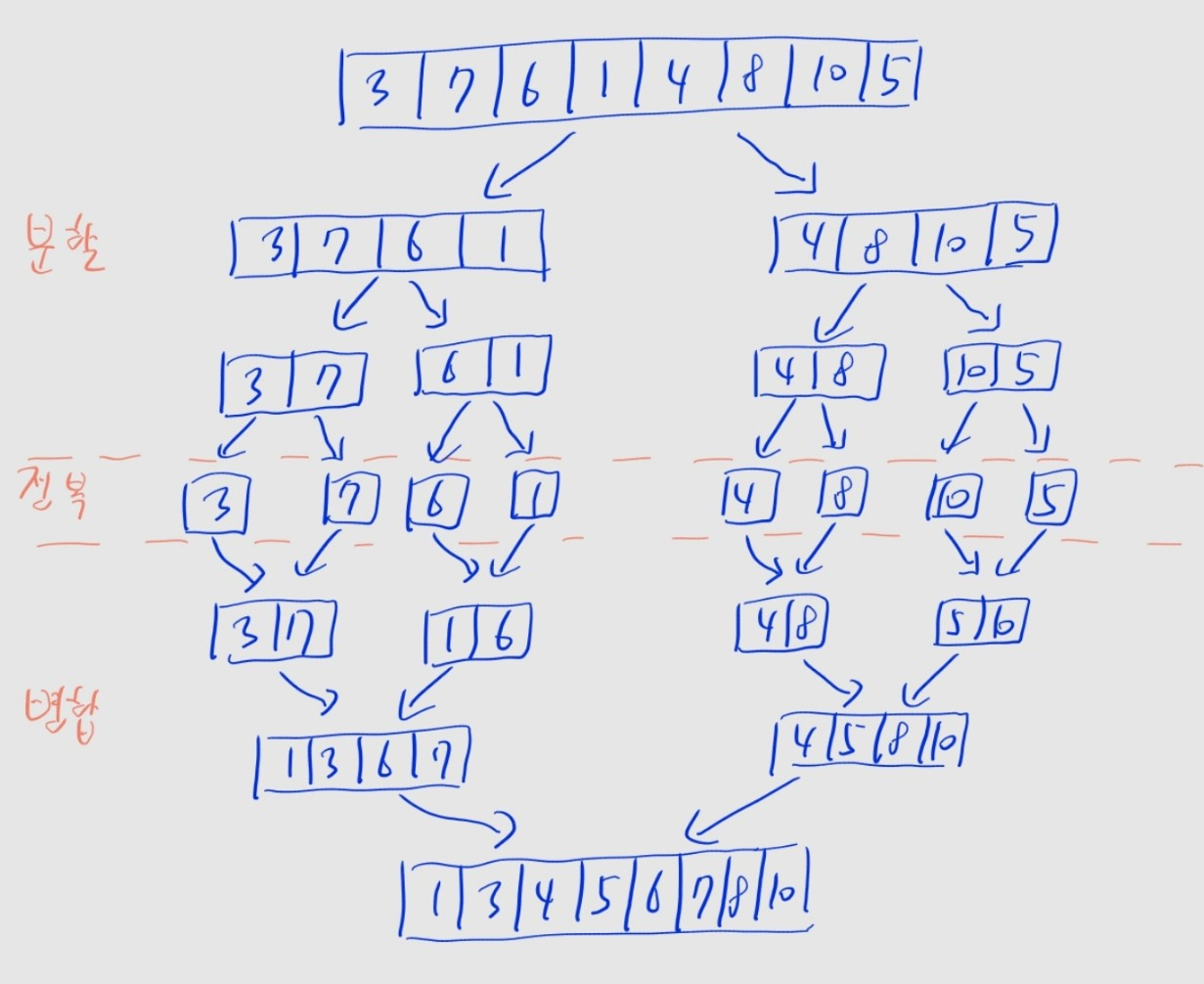
- 재귀함수를 이용해...
- 함수 내 재귀 호출로, 문제를 부분문제로 분할
- 재귀 함수의 종료조건을 통해, 부분문제를 정복
- 아직 종료되지 않은 이전 함수에서 재귀호출 결과를 조합
- 참 이건 뭐라 설명하기가 애매하다. 문제를 많이 풀어서 익숙해져야 합니다. 위 글에 있는 색종이 자르기 문제를 복습하도록 하세요.

상록님 믿고 이제 공부 안 할게요