[PS] 깊이 우선 탐색, 너비 우선 탐색

방법이있지·2025년 5월 30일

Problem Solving 크래프톤 정글

[정글 1-4주차] Problem Solving

목록 보기

18/26

정글에선 넓고 얕은 인간관계와 좁고 깊은 인간관계 사이에서 고민을 하게 됩니다.

하지만 DFS든 BFS든 모든 노드를 만나듯, 어떻게든 모두랑 친해질 수 있지 않을까요?

~~제가 어느 쪽을 더 좋아하는지는 비밀로 하겠습니다.~~

그래프의 탐색

배열이나 해시테이블에선 인덱스 / 키를 이용해 원하는 원소에 접근할 수 있었습니다.
하지만 그래프에선 특정 노드에서 시작해서, 간선을 타고 이동하면서 노드를 직접 찾아야 해요.
이때 탐색 경로가 다양할 수 있는데, 경로를 정하는 방식으로는 크게 깊이우선 / 너비우선 탐색 2가지 방식이 있습니다.

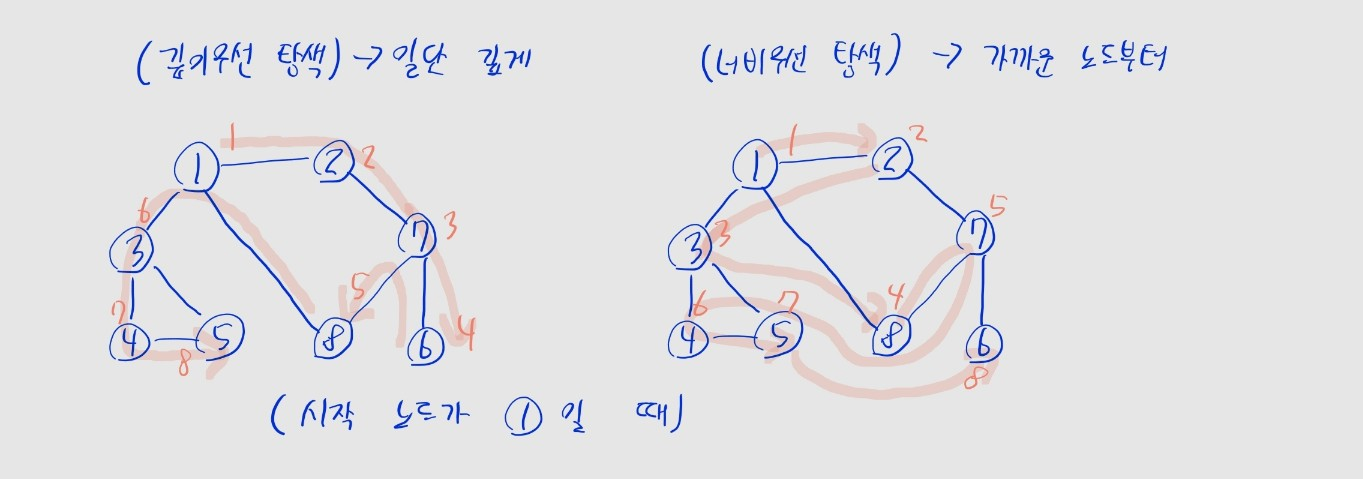
깊이우선 탐색: 그래프 내 가능한 한 깊게 노드를 방문하는 탐색 방식
너비우선 탐색: 그래프 내 현재 노드와 인접한 노드부터 순차적으로 방문하는 탐색 방식

깊이우선탐색 (DFS)

스택을 이용한 DFS

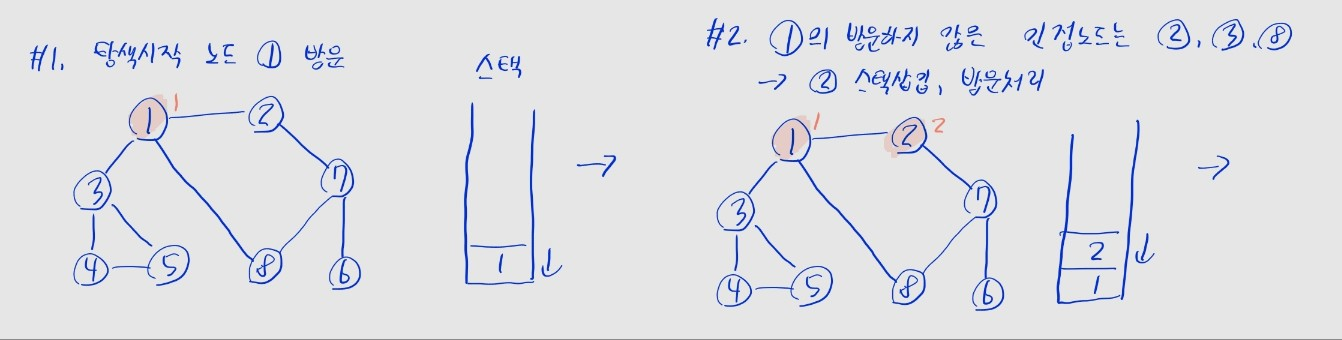
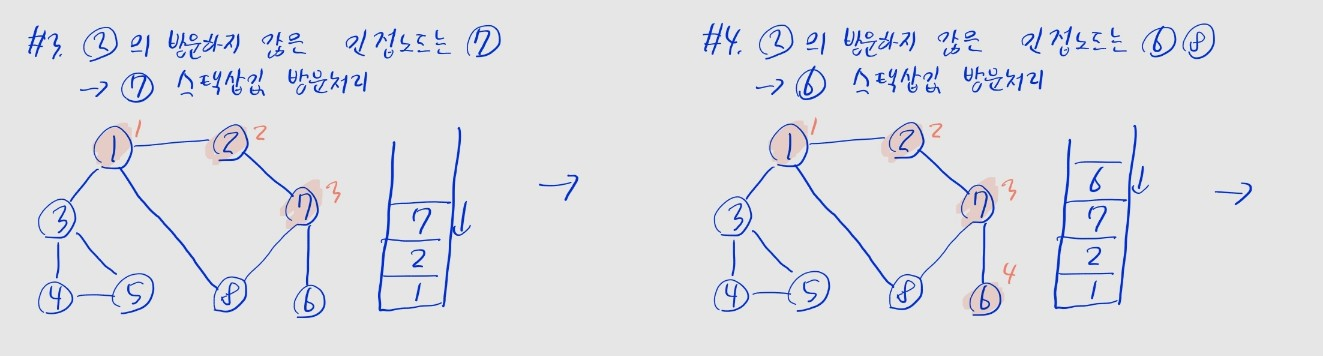
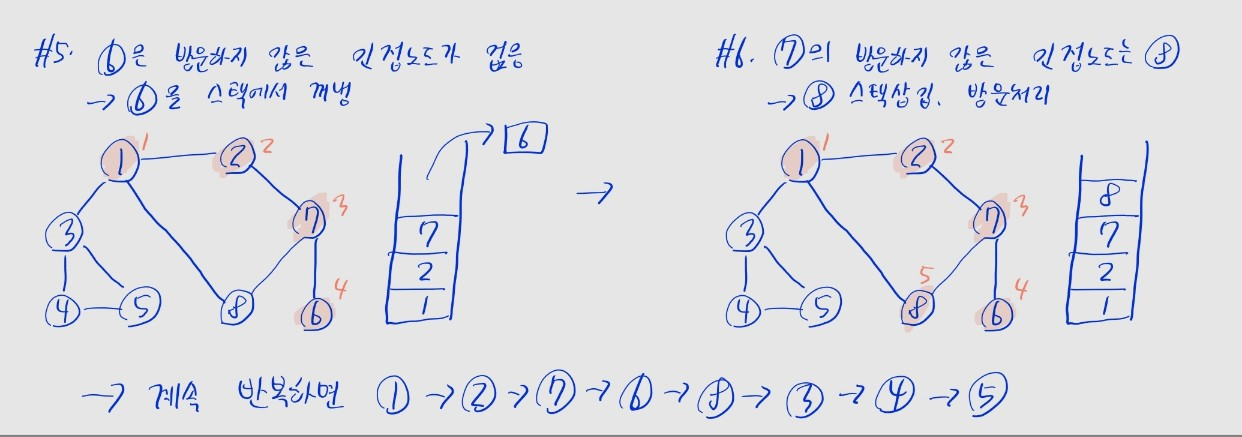
(1) 탐색 시작 노드를 스택에 삽입하고, 방문 처리를 함
(2) 스택의 최상단 노드에 방문하지 않은 인접 노드를 확인
- 방문하지 않은 인접 노드를 스택에 넣고, 방문 처리를 함
- 여러 개인 경우, 일반적으로 노드 번호가 제일 작은 노드를 선택
- 없을 경우: 스택에서 최상단 노드를 꺼냄
(3) 더 이상 (2)를 수행할 수 없을 때까지 반복

재귀를 이용한 DFS

실제로 DFS는 스택보단, 더 코드 구현이 쉬운 재귀를 이용해서 구현하는 편
- 재귀 함수를 호출할 때마다 호출한 함수는 시스템상 스택에 쌓이기 때문에, 비슷하게 구현 가능


# 인접 리스트
graph = [
    [],         # 0번노드는 사용 안 함
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

# 각 노드의 방문 여부
visited = [False] * 9

본 예제에는 1번부터 8번까지 8개의 노드가 있음
- 앞선 그림에서의 그래프와 동일한 그래프
graph 2차원 리스트로, 그래프를 인접 리스트 형태로 표현
- graph[i]는 시작 노드 i와 연결된 인접 노드의 리스트
- graph[0]은 편의상 비워둠
- e.g., graph[1] -> [2, 3, 8]: 1번 노드는 2, 3, 8번 노드와 연결됨
visited 리스트로 각 노드의 방문 여부를 표현
- visited[i]가 True면 i번 노드를 방문했고, False면 방문하지 않은 상태

def dfs(graph, x, visited):
    # (1) 노드 x를 방문 처리
    visited[x] = True
    print(x, end=" ")

    # (2) 미방문한 인접 노드를 재귀적으로 방문
    for i in graph[x]:      # 노드 x의 인접 노드 순회
        if not visited[i]:  # 인접 노드가 미방문 노드인 경우
            dfs(graph, i, visited)  # 재귀 호출

노드를 스택에 삽입 하고 방문 처리 하는 대신, 노드를 매개변수로 보내 재귀 호출하고 방문 처리
dfs(x) 함수는 x번 노드를 방문하고, 미방문한 인접 노드 i를 재귀적으로 방문
- dfs(i)가 실행되는 동안에도 dfs(x)은 아직 종료되지 않았음
- 마치 스택에서 노드 i 밑에 노드 x가 남아 있는 것과 유사
스택에서 최상단 노드를 꺼내는 대신, 현재 실행 중인 재귀함수를 종료
- dfs(i)가 종료되면, 이전에 호출된 dfs(x)로 돌아오게 됨

# DFS 함수 호출
dfs(graph, 1, visited) # 1 2 7 6 8 3 4 5

1번 노드부터 DFS 탐색을 시작
최종 순서는 1 -> 2 -> 7 -> 6 -> 8 -> 3 -> 4 -> 5

너비우선탐색 (BFS)

큐를 이용한 BFS

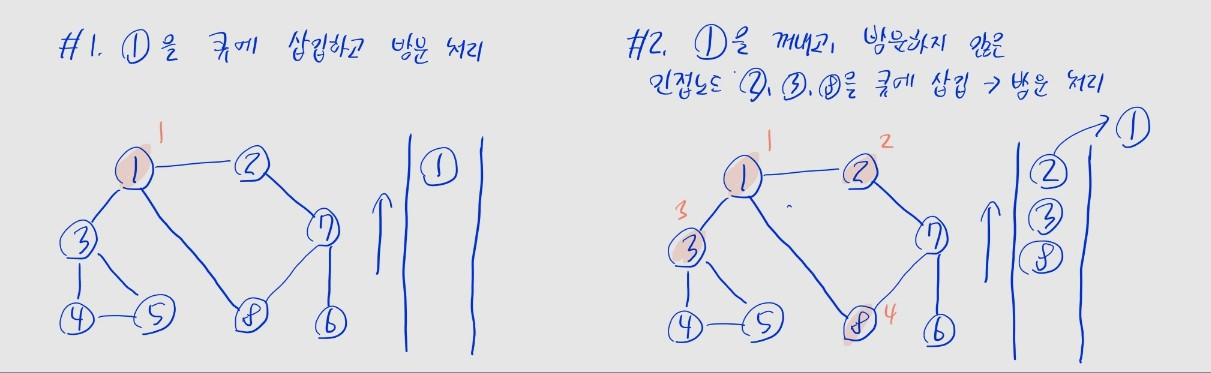
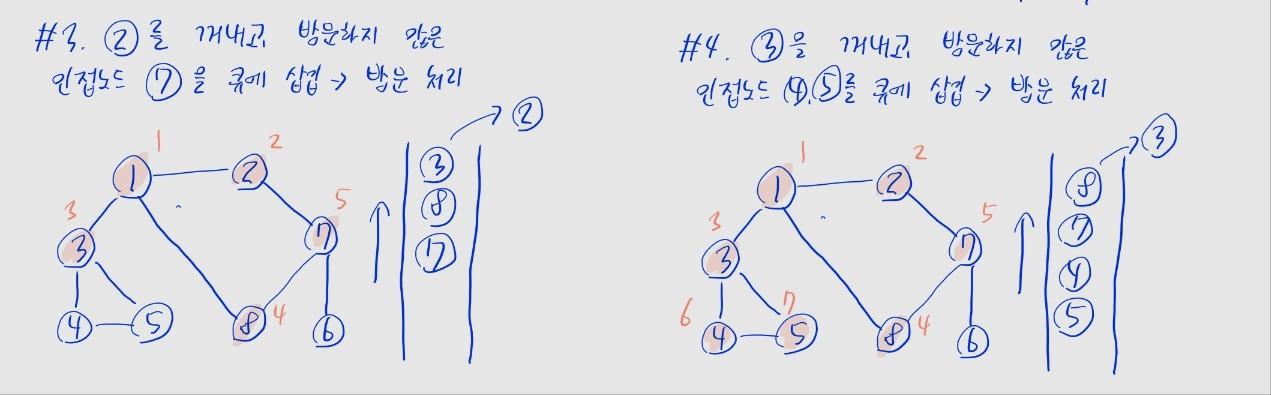
(1) 탐색 시작 노드를 큐에 삽입하고, 방문 처리를 함
(2) 큐에서 노드를 꺼내고, 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
- 여러 개인 경우, 일반적으로 번호가 낮은 순 -> 높은 순으로 삽입
(3) 더 이상 (2)를 수행할 수 없을 때까지 반복

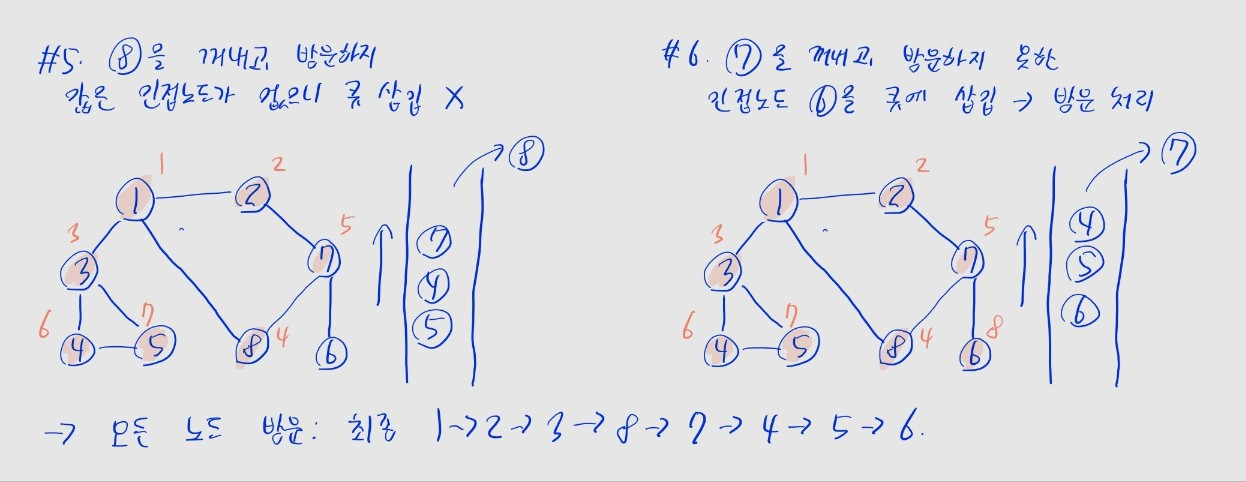
⚠️ BFS는 시작 노드와의 거리가 가까운 노드부터 탐색합니다.

거리: 두 노드 사이 거쳐야 하는 간선 수
- 우선 위 예제에선 시작 노드 (1) 방문
- 이후 거리가 1인 노드 (2, 3, 8) 방문
- 이후 거리가 2인 노드 (7, 4, 5) 방문
- 마지막으로 거리가 3인 노드 (6) 방문
이러한 특징 덕분에, 간선의 가중치가 모두 동일한 경우 최단 거리를 구하는 문제에서도 사용할 수 있습니다.
- 가중치가 명시되지 않은 그래프에선 다 1로 동일하게 간주할 수 있다는 점 기억하시죠?

graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

# 시작 노드와의 거리. 방문하지 않은 노드는 None.
distance = [None] * 9

🤗 BFS로 거리 순으로 노드를 반환한다는 특징을 이용해, 이번엔 visited 말고 distance 배열을 만들어 보겠습니다.

distance[i]엔, i번째 노드를 방문할 때 i번 노드와 시작 노드 간 거리를 계산해 저장
방문하지 않아 거리를 아직 계산하지 못한 경우 None으로 표시

from collections import deque

def bfs(graph, start, distance):
    # 큐에 시작 노드를 삽입
    queue = deque([start])
    # 시작 노드와 시작 노드 간 거리는 0
    distance[start] = 0

    while queue:
        # 큐에서 노드 x를 꺼냄
        x = queue.popleft()
        print(x, end=" ")

        # 아직 방문하지 않은 인접 노드 탐색
        for i in graph[x]:
            if distance[i] is None:
                # 모두 큐에 삽입
                # 거리: 현재 노드의 거리 + 1
                queue.append(i)
                distance[i] = distance[x] + 1

deque를 이용해서 큐를 구현할 수 있음
시작 노드의 거리는 0으로 둠
매번 큐에 인접 노드를 삽입할 때마다, 인접 노드의 거리는 현재 노드의 거리 + 1로 계산
- 방문 여부는 앞서 말했듯이 distance[i]가 None인지 아닌지로 체크

bfs(graph, 1, distance) # 1 2 3 8 7 4 5 6

print("\n거리 정보")
for i in range(1, 9):
    print(f"{i}번 노드: {distance[i]}")

# 거리 정보
# 1번 노드: 0
# 2번 노드: 1
# 3번 노드: 1
# 4번 노드: 2
# 5번 노드: 2
# 6번 노드: 3
# 7번 노드: 2
# 8번 노드: 1

이렇게 거리 정보를 저장해 두면, "출발점에서 도착점까지 최단 거리를 구하시오" 유형의 문제에서 잘 써먹을 수 있음

DFS, BFS의 시간 복잡도

노드의 개수가 $N$ , 간선의 개수가 $E$ 일 때
위 코드와 같이 인접 리스트를 통해 그래프를 구현하는 경우
- 모든 노드를 1번씩 방문, $O(N)$
- 모든 간선을 1번씩 확인, $O(E)$
$O(N + E)$ , DFS든 BFS든 마찬가지

🤔 왜 DFS, BFS를 구현할 때 인접 행렬이 아니라 인접 리스트를 사용하나요?

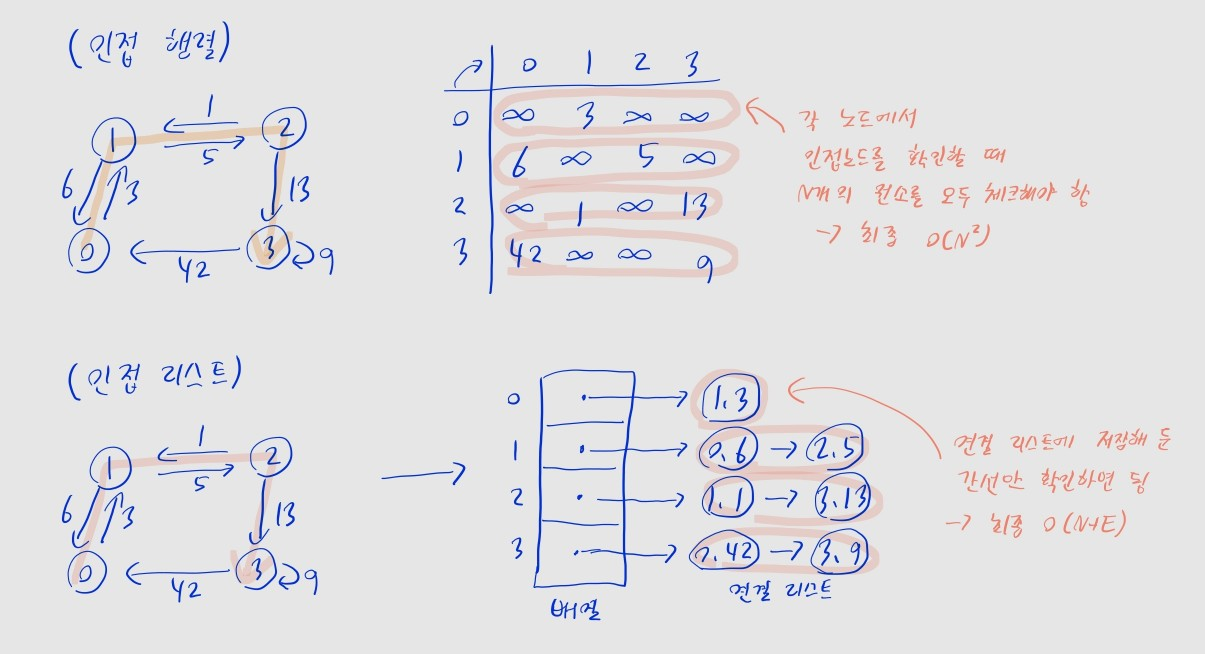
인접 행렬의 경우, 인접 노드를 확인할 때 모든 노드에 대해 연결 여부를 확인해야 하므로 $O(N)$ 이 소요됩니다.
- 모든 노드에 대해 인접 노드를 확인하는 과정에서, 인접 행렬의 최종 시간 복잡도는 $O(N^2)$ 가 됩니다.
반면 인접 리스트는 미리 리스트에 저장해 둔 인접 노드만 확인하면 됩니다.
- 즉 최종 시간 복잡도는 $O(N + E)$ 가 됩니다.

둘 중에 뭘 써야 해요??

🐶 단순히 모든 노드를 탐색해야 하는 경우

시간 복잡도도 동일해서 뭘 쓰든 상관없습니다.
다만 재귀를 사용하는 DFS는 sys.setrecursionlimit()로 깊이 제한을 늘려 줘야 하는 번거로움이 있습니다.
그래서 전 웬만해선 BFS로 풀이하는 편입니다.

🐶 노드 간 최단 거리를 확인해야 하는 경우

앞서 설명했듯이, 가까운 노드부터 차례대로 탐색하는 BFS를 사용해야 합니다.
각 노드의 거리 정보를 계산한 뒤, 문제의 요구에 맞게 알맞은 값을 반환합니다.

🐶 [경우의 수를 찾아야 하는 경우]

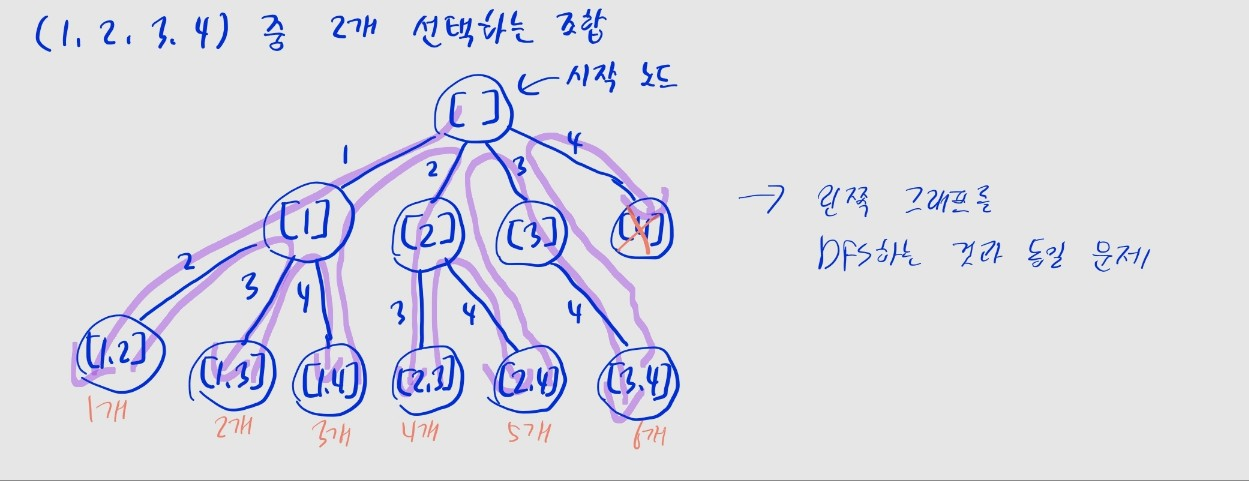
N-Queen, 순열/조합 구하기같은 문제들은 DFS 문제의 일종으로 볼 수 있습니다.

예를 들어, 조합 문제는 사실 DFS로 그래프를 탐색하는 문제입니다.
- 노드는 지금까지 선택한 숫자의 수 (e.g., 현재까지 2 선택)
- 간선은 다음 선택지 (e.g., 다음 숫자를 3로 고를지, 4로 고를지)로 볼 수 있습니다.
한번에 한 경로를 따라 깊게 탐색하는 DFS를 사용해야, 지금까지 선택한 숫자들의 맥락을 유지하며 다음 숫자를 고를 수 있습니다.
- BFS로는 매번 탐색 경로가 바뀌니까 이게 어렵겠죠.

문제풀이

1260. DFS와 BFS

백준 / 실버 2 / 1260. DFS와 BFS

import sys
from collections import deque
sys.setrecursionlimit(10 ** 6)

N, M, V = map(int, input().split())
graph = [[] for _ in range(N + 1)]
visited_dfs = [False] * (N + 1)
visited_bfs = [False] * (N + 1)

# 양방향임에 유의하기
for _ in range(M):
    a, b = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a)

for i in range(1, N + 1):
    graph[i].sort()
    
# DFS
def dfs(x, graph, visited):
    print(x, end=" ")
    visited[x] = True
    
    for i in graph[x]:
        if not visited[i]:
            dfs(i, graph, visited)

dfs(V, graph, visited_dfs)
print()

# BFS
def bfs(start, graph, visited):
    queue = deque([start])
    visited[start] = True
    
    while queue:
        x = queue.popleft()
        print(x, end=" ")
        for i in graph[x]:
            if not visited[i]:
                queue.append(i)
                visited[i] = True

bfs(V, graph, visited_bfs)

위에 써 놓은 코드를 거의 그대로 쓰면 됨
양방향이므로 graph[a].append(b), graph[b].append(a) 양쪽 다 해 줘야 함에 유의
인접 노드가 여러 개면 노드 번호가 작은 노드부터 들려야 하므로, graph 내 리스트를 모두 정렬해야 함
이 문제에서는 BFS에서 굳이 거리 계산을 안 해도 되서, DFS처럼 방문 여부만 체크함

18352. 특정 거리의 도시 찾기

백준 / 실버 2 / 18352. 특정 거리의 도시 찾기

from collections import deque
import sys

input = sys.stdin.readline

# 도시, 도로, 목표 최단거리, 출발 도시
N, M, K, X = map(int, input().split())
graph = [[] for _ in range(N + 1)]

# 인접 리스트
for _ in range(M):
    a, b = map(int, input().split())
    graph[a].append(b)
    
# 각 도시의 거리정보. 미방문 시 None
dist = [None] * (N + 1)

def bfs(graph, start, dist):
    dist[start] = 0     # 출발 도시의 거리는 0
    queue = deque([start])

    while queue:
        i = queue.popleft()
        for j in graph[i]:
            if dist[j] is None:
                # 인접 도시의 거리는
                # 현재 도시의 거리 + 1로 계산
                dist[j] = dist[i] + 1
                queue.append(j)    

bfs(graph, X, dist)

# 최단 거리가 K
count = 0

for i in range(1, N + 1):
    if dist[i] == K:
        print(i)
        count += 1

if count == 0:
    print(-1)

위에서 설명한 방법대로, 각 도시의 최단거리를 저장할 리스트 생성
BFS로 각 도시의 최단거리를 확인하며, 인접 도시의 거리는 현재 도시의 거리 + 1로 계산

방법이있지

뭔가 만드는 걸 좋아하는 개발자 지망생입니다. 프로야구단 LG 트윈스를 응원하고 있습니다.