백준 / 골드 4 / 10830. 행렬 제곱

주인장이 구름사다리에 점프해서 올라타려다가 허벅지 쪽에 근육통이 심하게 와서 실성을 했습니다. 글이 두서 없으면 양해 바랍니다.

생각해봅시다!!

• 행렬 $A$의 $B$제곱을 구하고, 각 원소를 $1000$으로 나머지 연산하는 문제입니다.
• 입력을 보니 $1 \leq B \leq 100,000,000,000$... 아직 구현을 해 보지는 않았지만 단순히 곱셈만 반복했다간 시간 초과가 뜰 것 같습니다.
• 분할 정복을 통해서 중복되는 연산을 줄이는 방법을 쓰는 게 좋습니다. 그 방법은 밑에서 소개

행렬곱 구하기

• 우선 두 행렬 $A, B$의 행렬곱을 반환하는 함수 matmul(A, B)부터 만들어 보겠습니다.
• 행렬 $A, B$의 곱 $AB = C$로 둘 때, $C$의 $i$행 $j$열 값은 다음과 같이 계산합니다.
  • $A$의 $i$행, $B$의 $j$행의 각 원소를 순서대로 짝지어 곱한 뒤 더합니다.
• e.g., $\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}\begin{pmatrix}5 & 6 \\ 7 & 8\end{pmatrix} = \begin{pmatrix}19 & 22 \\ 43 & 50\end{pmatrix}$
  • 자세한 연산과정은 아래 사진을 보세요.

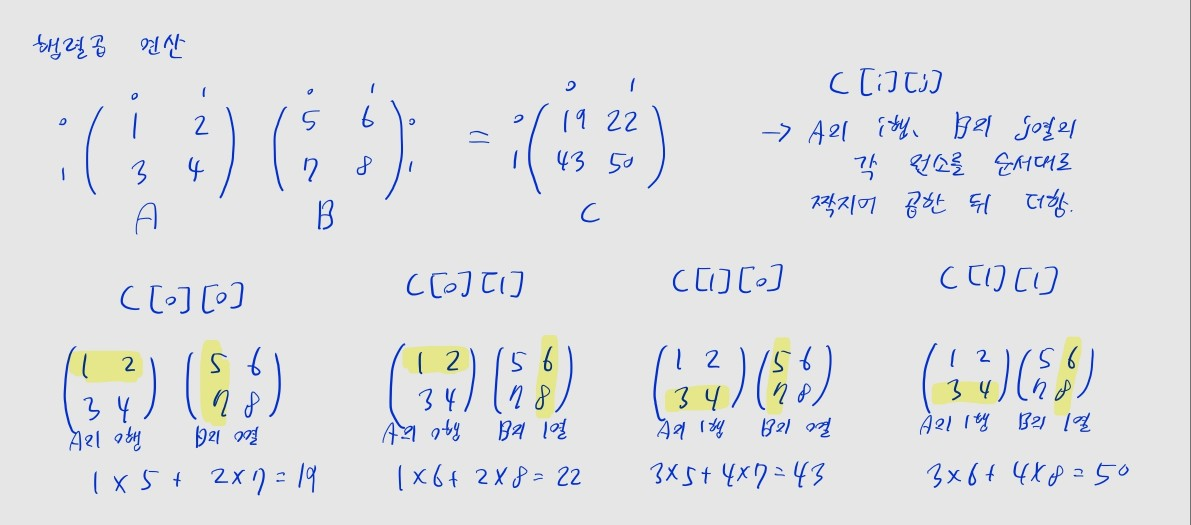
• matmul 함수는 아래 코드와 같이 구현할 수 있습니다.

# 행렬 A, B 곱하기
def matmul(A, B):
    result = [[0] * N for _ in range(N)]
    for i in range(N):
        for j in range(N):       
            # AB의 행렬곱 C의 i행 j열
            # A의 i행, B의 j열 모든 원소를 서로 곱하고 합
            value = 0
            for k in range(N):
                value += (A[i][k] * B[k][j])
            result[i][j] = value % 1000
    return result

• A와 B의 행렬곱을 result로 둘 때
• for i in range(N), for j in range(M) 이중 반복문으로 result[i][j]를 계산합니다.
  • 이때 A의 i행과 B의 j열의 원소를 순서대로 짝지어 곱하게 되는데, 행렬의 크기가 $N$행 $N$열이므로 각 행 및 열에도 $N$개의 원소가 있게 됩니다.
  • for k in range(N)으로 k를 순회하며, A[i][k]와 B[k][j]의 곱을 value에 더합니다.
• 이후 value 값을 $1,000$으로 나머지 연산 한 뒤, A[i][j]에 저장하면 됩니다.

🤔 저게 최종 정답이 아닐 수도 있는데 벌써 1000으로 나눠도 되나요? 문제가 생기지 않나요?

• $a$와 $b$ 간의 덧셈, 곱셈 연산의 경우, $a$와 $b$ 각각에 나머지 연산을 한 뒤 덧셈/곱셈을 하는 거랑, $a+b$나 $a \times b$의 결괏값에 나머지 연산을 하는 것엔 결과 차이가 없습니다.
• 따라서 최종 정답이 이상한 값으로 바뀔 우려는 안 하셔도 됩니다.

시간 복잡도

• 3번의 for문을 돌면서, 행렬의 크기가 $N \times N$일 때 $O(N^3)$이 소요됩니다.
• 단 $2 \leq N \leq 5$이므로 많아봤자 $125$번 연산이 발생하므로, 걱정할 필요는 없습니다.

행렬제곱 구하기

• 이후 행렬 grid을 times번 곱하는 함수 power(grid, times)를 만들어 보겠습니다.

def power(grid, times):
    if times == 1:
        return grid
    else:
        half = power(grid, times // 2)
        if times % 2 == 0:
            return matmul(half, half)
        else:
            return matmul(matmul(half, half), grid)

• times가 1이면 행렬곱을 할 필요가 없으니 grid를 그냥 반환하면 됩니다.
• times가 2 이상이고 짝수인 경우
  • grid의 times // 2제곱을 계산해 half 변수에 저장하고
  • half와 half 함수의 행렬곱을 곱해 반환합니다.
• times가 2 이상이고 홀수인 경우
  • grid의 times // 2제곱을 계산해 half 변수에 저장하고
  • half와 half를 행렬곱합니다.
  • 그 결과값에 grid를 행렬곱해 반환합니다.

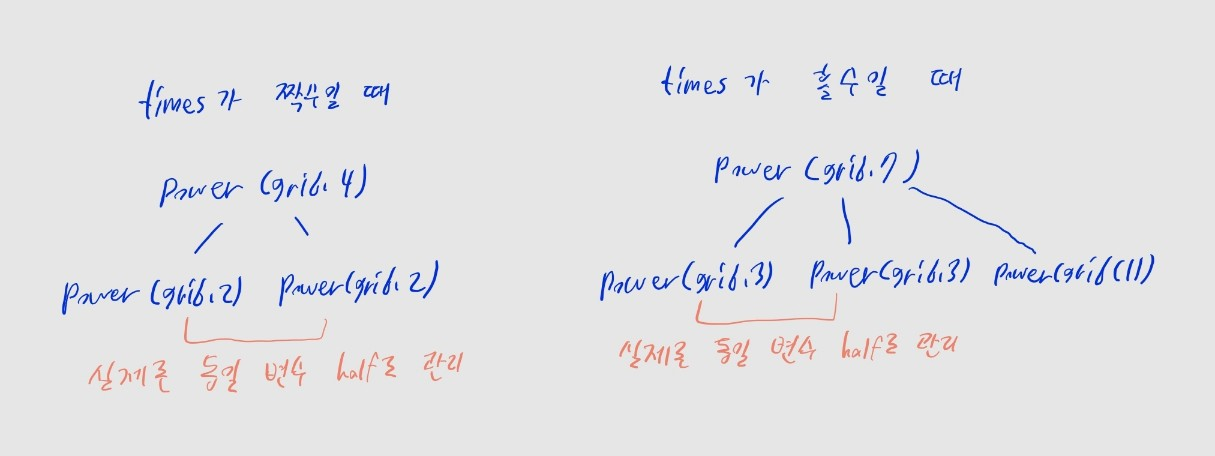
🤔 왜 굳이 half 변수를 사용하나요? matmul(power(grid, times // 2), power(grid, times // 2))로 계산해도 결과는 같지 않나요?

• 결과가 동일한데 굳이 power 함수를 2번 호출할 필요는 없습니다. 특히 power 함수는 재귀 호출로 인해 종료될 때까지 시간이 오래 걸리므로, 호출을 최소화하는 게 답입니다.

🤔 times가 홀수일 때 times // 2, times // 2, 1 제곱 3개로 쪼개는 것보다, times // 2, times // 2 + 1 제곱 2개로 쪼개는 게 효율적이지 않나요? 3개로 쪼개면 행렬곱 연산(matmul)을 한번 더 하게 되잖아요.

• 앞서 봤듯이 matmul은 최대 연산이 $125$번까지만 발생하므로, 많이 호출해도 성능상 큰 문제는 없습니다. 반면 power는 재귀함수의 성능 문제 때문에 호출을 덜 하는 게 답입니다.
• 본 코드에선 power(grid, times // 2) 2개를 동일한 변수 half로 관리하므로 효율적입니다.
• 반면 power(grid, times // 2)와 power(grid, times // 2 + 1) 2개로 쪼개면, 두 번의 서로 다른 재귀 호출이 발생하므로 비효율적입니다.

풀이

N, times = map(int, input().split())

# 행렬 A, B 곱하기
def matmul(A, B):
    result = [[0] * N for _ in range(N)]
    for i in range(N):
        for j in range(N):       
            # AB의 행렬곱 C의 i행 j열
            # A의 i행, B의 j열 모든 원소를 서로 곱하고 합
            value = 0
            for k in range(N):
                value += (A[i][k] % 1000) * (B[k][j] % 1000)
            result[i][j] = value % 1000
    return result

# 행렬 grid의 times 제곱
def power(grid, times):
    if times == 1:
        return grid
    else:
        half = power(grid, times // 2)
        if times % 2 == 0:
            return matmul(half, half)
        else:
            return matmul(matmul(half, half), power(grid, 1))
        
grid = []
for _ in range(N):
    grid.append(list(map(int, input().split())))

# 맨 처음 나머지 연산
for i in range(N):
    for j in range(N):
        grid[i][j] = grid[i][j] % 1000

answer = power(grid, times)
for i in range(N):
    print(*answer[i])

• 행렬의 입력을 받은 후, 모든 원소에 대해 $1,000$으로 나머지 연산을 해 두는 걸 잊지 맙시다!!
• 가끔씩 행렬의 $1$제곱을 구하라고 하는 테스트 케이스가 있습니다. 이때 1000으로 나머지 연산을 하지 않고 바로 행렬을 반환해 버리면, 얄짤 없이 오답 처리됩니다.

시간 복잡도

• 문제에서 $N\times N$ 행렬의 $B$제곱을 구해야 할 때
• $B$를 반절씩 쪼개므로 재귀는 약 $\log B$ 단계 이루어집니다.
  • 각 재귀 단계에서 matmul 함수로 행렬의 모든 성분을 순회하므로, $O(N^3)$가 소요됩니다.
• 즉 시간 복잡도는 $O(N^3 \log B)$
  • $N \leq 5$므로 이쪽은 무시해도 되고
  • $B \leq 100,000,000,000$지만 $\log B \leq$ 약 $27$dl이므로 성능상 문제가 없습니다.

기억할 점

• 분할 정복에선 무조건 무조건 무조건 중복되는 계산을 최소화해야 한다.