백준 / 골드 4 / 1707. 이분 그래프

......죄송합니다.

생각해봅시다!!

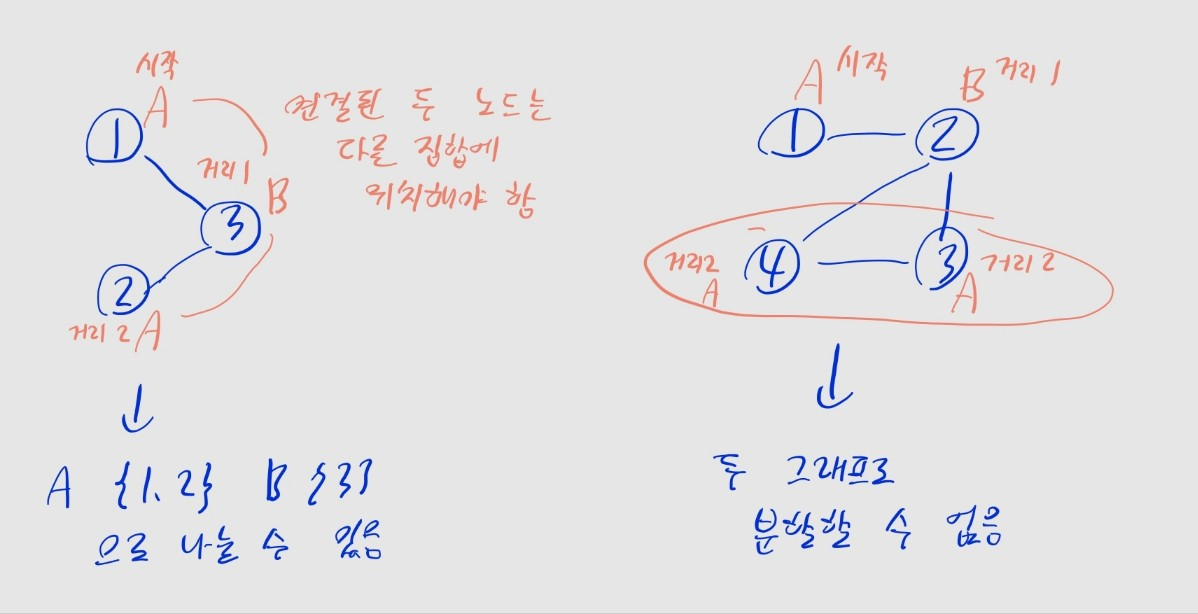
• 같은 집합에 속한 노드끼리 서로 인접하지 않으려면,
• 간선으로 연결된 두 노드는 각각 다른 집합에 위치해야 합니다.
• 본 글에서는 집합 A, 집합 B라는 표현을 사용하겠습니다.

BFS 사용하기

• BFS로 노드를 탐색하면서, 각 노드를 집합 A or 집합 B로 분류합니다.
• 앞서 말했듯이 간선으로 연결된 두 노드는 다른 집합에 위치해야 합니다."
• 즉, 이러한 방식으로 각 노드를 A나 B로 분류합니다.
  • 시작 노드는 집합 A로
  • 시작 노드에서 간선 1개 떨어진 노드는 집합 B로
  • 시작 노드에서 간선 2개 떨어진 노드는 집합 A로
  • ...같은 방식으로 B -> A -> B 순으로 노드들을 분류
• 단, 이 과정에서 인접한 두 노드의 집합이 동일해지는 경우,
  • 규칙을 위반하므로 이분 그래프로 나눌 수 없습니다.

• DFS로도 풀 수 있지만 제가 BFS를 더 좋아해서 BFS로 풀겠습니다.

방문여부 확인

def check(graph):
    N = len(graph) - 1    # 노드 수

    # 방문하지 않은 경우 False
    # 방문한 경우 'A' or 'B'
    visited = [False] * (N + 1)
    
    # 뒷 코드에서 계속

• visited 배열은 방문 여부와 집합 정보를 함께 저장합니다.
  • 방문하지 않은 경우 False
  • 방문한 경우, 분류된 집합에 따라 A or B

BFS 탐색 및 집합 분류

def check(graph):
	# 앞 코드에서 이어짐
    def bfs(x):
        queue = deque([x])
        visited[x] = 'A' # 시작 노드는 집합 A로 분류
        
        while queue:
            i = queue.popleft()
            for j in graph[i]:
                
                # 인접 노드 중 미방문한 노드 
                if not visited[j]:
                   # 현재 노드가 'A'면 인접 노드는 'B'로
                   # 현재 노드가 'B'면 인접 노드는 'A'로 분류해야 함
                   flag = 'B' if visited[i] == 'A' else 'A'
                   visited[j] = flag
                   queue.append(j)
                
                # 인접 노드 중 동일 집합의 노드가 존재
                elif visited[j] == visited[i]:
                    return False 
        return True
    # 뒤 코드로 이어짐

• bfs 함수는 큐에서 팝한 노드 i와 인접한 노드 j를 확인할 때
• j가 미방문 노드인 경우
  • 현재 노드 i가 A면, 인접 노드 j는 B로
  • 현재 노드 i가 B면, 인접 노드 j는 A로 분류합니다.
• j가 이미 방문한 노드인데, i와 동일 집합으로 분류된 경우
  • 인접한 노드 i, j가 동일 집합에 속하니
  • 이분 그래프로 나눌 수 없음. False를 반환합니다.

def check(graph):
    # 앞 코드에서 이어짐
    for i in range(1, N + 1):
        if not visited[i]:
            
            # 이분 그래프를 만들 수 없는 경우 False 반환
            if not bfs(i):
                return False

    return True

• 그래프의 모든 노드가 연결되어 있지 않을 수 있으므로, bfs를 여러 번 시도해야 할 수도 있습니다.
• 즉 1부터 N+1까지 for문을 돌리고, 방문하지 않은 노드인 경우 bfs를 수행하여 연결된 노드들을 방문 처리하게끔 구현했습니다.

풀이

from collections import deque
import sys
input = sys.stdin.readline 
 
def check(graph):
    N = len(graph) - 1    # 노드 수

    # 방문하지 않은 경우 False
    # 방문한 경우 'A' or 'B'
    visited = [False] * (N + 1)
    
    def bfs(x):
        queue = deque([x])
        visited[x] = 'A' # 시작 노드는 집합 A로 분류
        
        while queue:
            i = queue.popleft()
            for j in graph[i]:
                
                # 인접 노드 중 미방문한 노드 
                if not visited[j]:
                   # 현재 노드가 'A'면 인접 노드는 'B'로
                   # 현재 노드가 'B'면 인접 노드는 'A'로 분류해야 함
                   flag = 'B' if visited[i] == 'A' else 'A'
                   visited[j] = flag
                   queue.append(j)
                
                # 인접 노드 중 동일 집합의 노드가 존재
                elif visited[j] == visited[i]:
                    return False 
        return True
                
    for i in range(1, N + 1):
        if not visited[i]:
            
            # 이분 그래프를 만들 수 없는 경우 False 반환
            if not bfs(i):
                return False

    return True

K = int(input())
for _ in range(K):
    
    V, E = map(int, input().split())
    graph = [[] for _ in range(V + 1)]
    for _ in range(E):
        u, v = map(int, input().split())
        graph[u].append(v)
        graph[v].append(u)
        
    if check(graph):
        print("YES")
    else:
        print("NO")

시간 복잡도

• BFS를 통해 모든 노드와 간선을 확인하므로
• 노드 수가 $N$개 간선 수가 $E$개일 떄 $O(N + E)$.

기억할 점

• 복잡한 조건을 만족해야 하는 문제에서는 일단 조건에 맞게 구성한 뒤, 진행 과정에서 모순이 발생하면 조건을 만족할 수 없는 것으로 판단한다.