백준 / 골드 2 / 13334. 철로

생각해봅시다!

• 동일한 사람의 집과 사무실을 구분할 필요는 없습니다. 뭐가 먼저 오든, 둘 다 철로 안에 들어오는지만 확인하면 됩니다.
  • 따라서 본 문제에서는 각 사람의 집 / 사무실이라는 표현 대신, 각 선분의 시작점 / 끝점이라는 표현을 쓰겠습니다. 철로 역시 철로의 시작점 / 끝점이라는 표현을 쓰겠습니다.
• 철로를 다양한 곳에 세울 수 있지만, 실제로는 철로의 끝점이 각 선분들의 끝점과 일치하는 경우만 고려해도 됩니다.
  • 철로를 그 위치에서 오른쪽으로 조금만 이동하더라도, 포함되는 선분의 수가 늘어날 가능성이 없습니다. 오히려 줄어들면 모를까.
    
• 철로를 설치할 지점을 왼쪽에서 오른쪽으로 옮겨가면서, 철로에 몇 개의 선분이 포함되는지 세면 됩니다.
  • 현재 포함된 선분을 리스트나 힙 등에 저장하면서 개수를 셀 수 있습니다. 다만 철로가 이동해서 선분이 더 이상 포함되지 않으면 빼 줄 필요가 있겠죠.
  • 이 풀이에선 최솟값을 빠르게 꺼낼 수 있어서 편리한 최소 힙을 쓰겠습니다.

풀이

import sys
import heapq

input = sys.stdin.readline
n = int(input())

lines = []               # 각 선분의 좌표
in_heap = []             # 시작점을 저장할 힙

for _ in range(n):
    h, o = map(int, input().split())
    # (끝점 좌표, 시작점 좌표)
    lines.append((max(h, o), min(h, o)))

lines.sort() # 끝점 좌표 기준으로 정렬

d = int(input())   # 철로의 길이

# 철근에 포함되는 사람들의 최대 수
answer = 0

• 우선 lines에는 각 선분의 시작점과 끝점을 저장합니다.
  • (max(h, o), min(h, o))로 (끝점, 시작점)이 되게끔 저장합니다.
• in_heap은 현재 철로에 들어가는 선분들의 시작점을 저장 및 관리하는 최소 힙입니다.
  • 나중에 철로를 이동시키면서, 철로 범위를 벗어나는 오래된 시작점들을 힙에서 제거합니다.
• 끝점 기준으로 lines를 정렬합니다.
  • 정렬할 원소에 튜플에 있는 경우, 첫 번째 값 기준으로 정렬됩니다.
  • 정렬을 하는 이유는, 철로를 각 선분의 끝점에 맞춰 설치하며 탐색하는 과정에서, 왼쪽에서 오른쪽순으로 탐색을 하기 위해서입니다.
• 우리가 구하고자 하는 정답인, 철로 내 선분의 최대 수는 answer에 저장합니다.

for end, start in lines:
    bridge_end = end
    bridge_start = bridge_end - d  # 철근의 시작점
    
    if bridge_start <= end:
        heapq.heappush(in_heap, start)
       
    while in_heap and in_heap[0] < bridge_start:
        heapq.heappop(in_heap)

    answer = max(answer, len(in_heap))
    
print(answer)

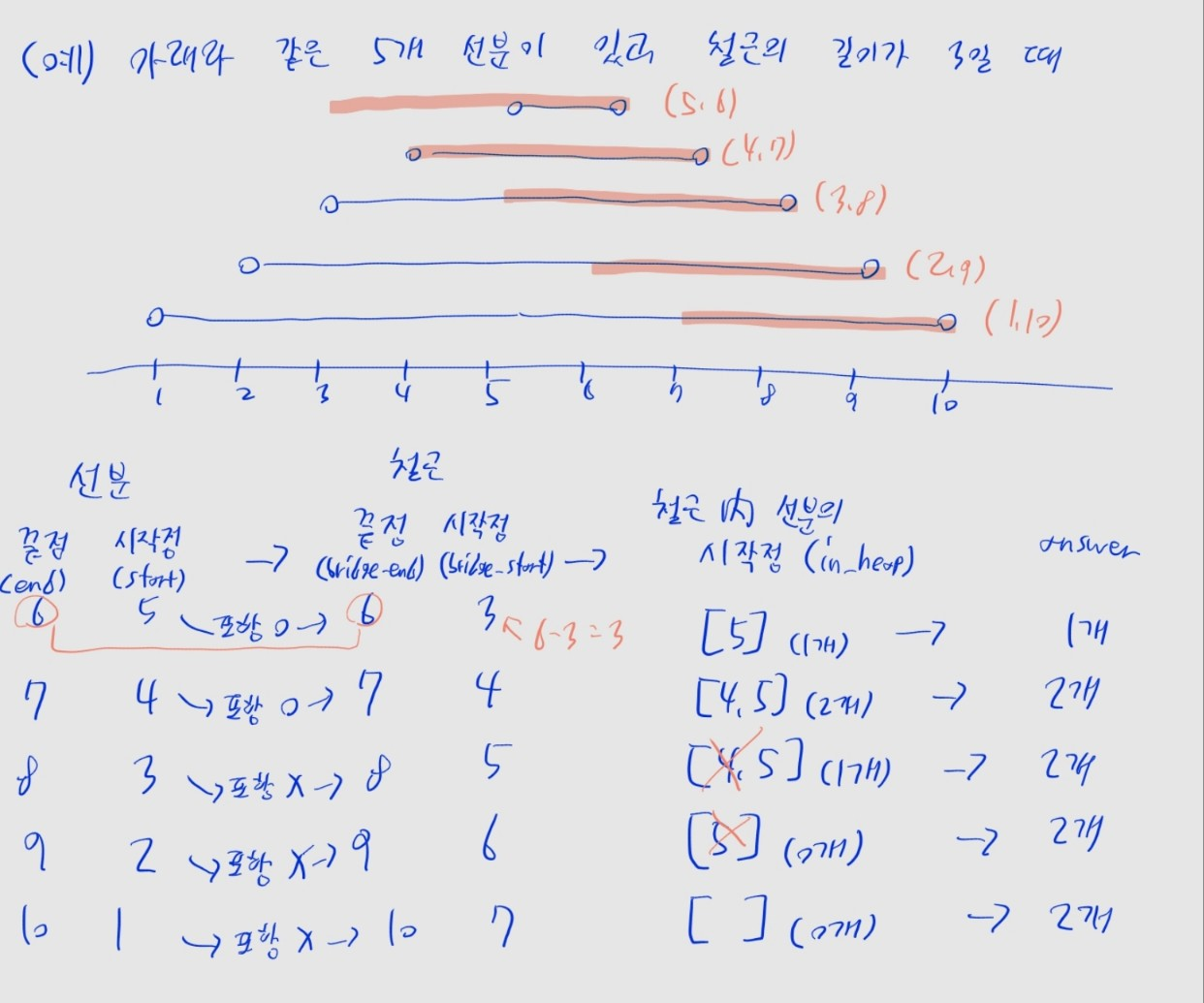
• 철로의 끝점이 각 선분들의 끝점인 경우만 고려하기로 했죠?
• 각 선분의 끝점(end)과 시작점(start)을 순회합니다.
  • 철로의 끝점(bridge_end)는 선분의 끝점(end)와 동일하게 설정합니다.
• 이후 철로의 끝점(bridge_end) - 철로의 길이(d)로 철로의 시작점 bridge_start을 계산합니다.
• bridge_start <= start인 경우엔 철로 안에 선분이 들어갈 수 있겠죠?
  • 이 경우 in_heap에 선분의 시작점인 start를 푸시해 줍니다.
• 이후 in_heap의 최솟값을 확인해, 현재 철로의 시작점보다 더 앞에 시작점이 있는 선분이 in_heap에 있는지 확인합니다.
  • 존재하는 경우, 해당 선분은 더 이상 현재 철로 범위에 포함되지 않으므로 heappop으로 제거해 줍니다.
  • 여러 개 존재할 수 있으니 while문을 사용합니다. 최소 힙 특성상 최솟값부터 반환되니, 제일 앞에 등장한 시작점부터 삭제됩니다.
• in_heap의 크기는 현재 철로에 포함되는 선분의 수입니다.
  • 즉 len(in_heap)이 answer보다 크면, answer를 갱신하면 됩니다.

풀이

import sys
import heapq

input = sys.stdin.readline
n = int(input())

lines = []               # 각 선분의 좌표
in_heap = []             # 각 선분의 시작점을 저장할 힙

for _ in range(n):
    h, o = map(int, input().split())
    # (종료점 좌표, 시작점 좌표)
    lines.append((max(h, o), min(h, o)))

lines.sort()

d = int(input())   # 철근의 거리


# 철근에 포함되는 사람들의 최대 수
answer = 0

for end, start in lines:
    bridge_end = end
    bridge_start = bridge_end - d  # 철근의 시작점
    
    if bridge_start <= start:
        heapq.heappush(in_heap, start)
       
    while in_heap and in_heap[0] < bridge_start:
        heapq.heappop(in_heap)

    answer = max(answer, len(in_heap))
    
print(answer)

시간 복잡도

• 선분의 개수가 $N$개일 때
• 선분들을 정렬하는 과정에서 $O(N \log N)$
• $N$개의 선분을 for문으로 순회할 때
  • 각 선분마다 heappush 및 heappop 연산 -> $O(\log N)$
  • 즉 $O(N \log N)$
• 최종 $O(N \log N)$, $N \leq 100,000$이므로 1초 안에 가능

기억할 점

• 이 문제처럼 위치를 이동하면서 구간 내 생기는 변화를 파악하는 알고리즘 문제를 슬라이딩 윈도우라고도 부른다.