백준 / 플래티넘 5 / 6549. 히스토그램에서 가장 큰 직사각형

생각해봅시다!

• 들쭉날쭉한 히스토그램에서 가장 큰 직사각형의 넓이를 구하라... 쉽진 않아 보입니다.
• 문제를 다시 한 번 읽어 볼까요? 히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다... 라고 써져 있네요.
• 밑변의 길이가 1인 직사각형의 넓이를 구하는 건 쉽죠! 그냥 1에다 높이만 곱해주면 되잖아요.
• 분할 정복을 이용해 풀어보도록 하죠...! 한번 히스토그램을 직사각형 하나하나로 쪼개봅시다.

넓이 계산 함수 만들기

# 인덱스 start부터 end까지 히스토그램의 최대넓이
def get_area(hist, start, end):
    
    # 종료조건 - 밑변의 길이가 1일 때
    if start == end:
        return hist[start]
    
    mid = (start + end) // 2
    
    # 왼쪽 영역 최댓값
    left = get_area(hist, start, mid)
    
    # 오른쪽 영역 최댓값
    right = get_area(hist, mid + 1, end)

	# 이후 풀이에 계속

• 히스토그램 hist의 start번째부터 end번째까지 직사각형의 넓이를 구하는 함수 get_area(hist, start, end)를 만들어 봅시다.
  • hist에는 각 직사각형의 높이가 리스트로 저장되어 있습니다.
• 일단 start == end (밑변의 길이가 1일 때)인 경우, 면적은 $1 \times 높이$이므로, 바로 hist[start]로 높이를 반환하면 됩니다.
• 문제는 밑변의 길이가 2 이상일 때입니다.
  • 일단 히스토그램을 절반으로 쪼갠 뒤, 각 영역에 대해 get_area 함수를 실행합니다.
  • 그러면 왼쪽 / 오른쪽 히스토그램 내 가장 큰 직사각형의 넓이를 구할 수 있습니다. 각각 left, right에 저장합시다.

• left, right 중에 최댓값을 반환하면 끝...? 이라고 생각했으면 크나큰 오산입니다.

나눈 두 영역을 가로지르는 영역 구하기

# get_area 함수 계속
# 왼쪽, 오른쪽을 가로지르는 영역 최댓값
l = mid
r = mid + 1

cross = 0 # 가로지르는 영역 중 최댓값을 저장
height = min(hist[l], hist[r]) # 현재 탐색한 막대기 중 최저높이
# 이후 풀이에 계속

탐색 준비

• start ~ mid번째 막대기, mid + 1 ~ end번째 막대기로 영역을 나누었을 때
  • 두 영역을 가로지르는 곳에 최대 직사각형이 존재할 수 있습니다. 가운데 영역도 살펴봐야겠죠.
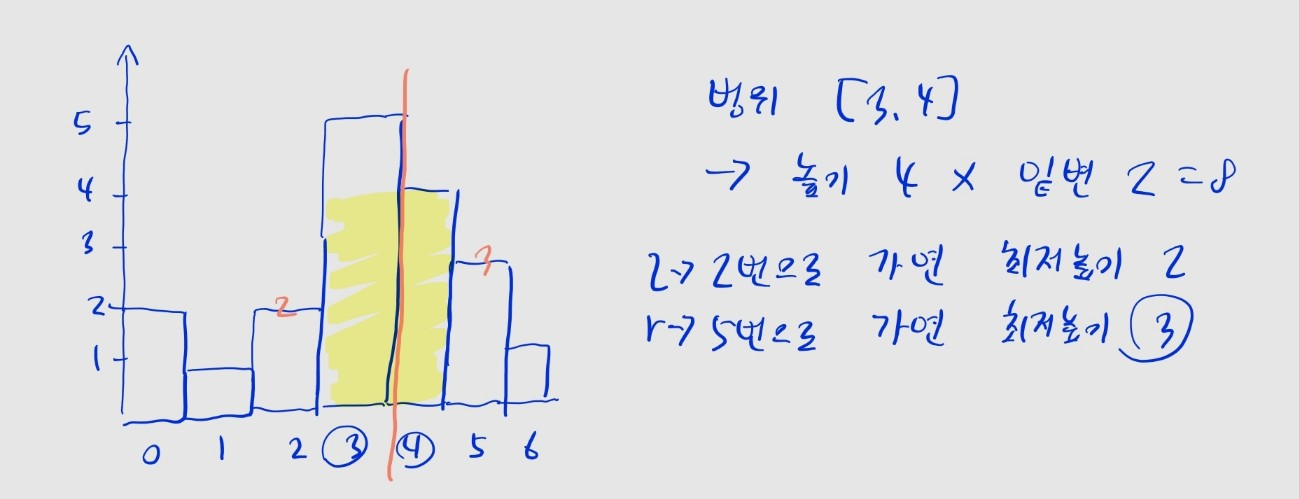
• 탐색할 첫 막대기를 l번째, 마지막 막대기를 r번째로 둘 때, 가운데부터 탐색하기 위해 l = mid, r = mid + 1로 둡니다.
• 가로지르는 영역의 넓이는 (밑변) * (막대기 높이 중 최솟값)이므로, 높이를 뜻하는 height 변수에는 앞으로 현재 탐색한 막대기들 중 최소 높이를 저장하겠습니다.
  • 일단 l, r 두 막대기만 확인했으니, hist[l]와 hist[r] 중 최솟값으로 초기화합니다.
• 공간을 넓혀 탐색하면서, 가로지르는 영역의 넓이의 최댓값을 cross 변수에 저장하고, 계속 갱신하겠습니다. 초깃값은 0으로 둡니다.

# get_area 함수 계속
while True:
    area = (r - l + 1) * height		# 현재 탐색한 막대기 넓이
    cross = max(area, cross)
    
    if l <= start and end <= r: # 모든 칸을 다 탐색
        break
    elif l <= start:    # j를 우측으로 이동
        height = min(height, hist[r + 1])
        r += 1
    elif end <= r:      # i를 좌측으로 이동
        height = min(height, hist[l - 1])
        l -= 1
    else: # 왼쪽을 이동할지, 오른쪽을 이동할지 판단
        r_height = min(height, hist[r + 1])
        l_height = min(height, hist[l - 1])
        if l_height > r_height:
            height = l_height
            l -= 1
        else:
            height = r_height
            r += 1
     return max(left, right, cross)
# get_area 함수 종료

탐색

• l번째부터 r번째 막대기까지의 넓이인 area로 (r - l + 1) * height를 구하고, 현재 cross보다 크면 갱신합니다.
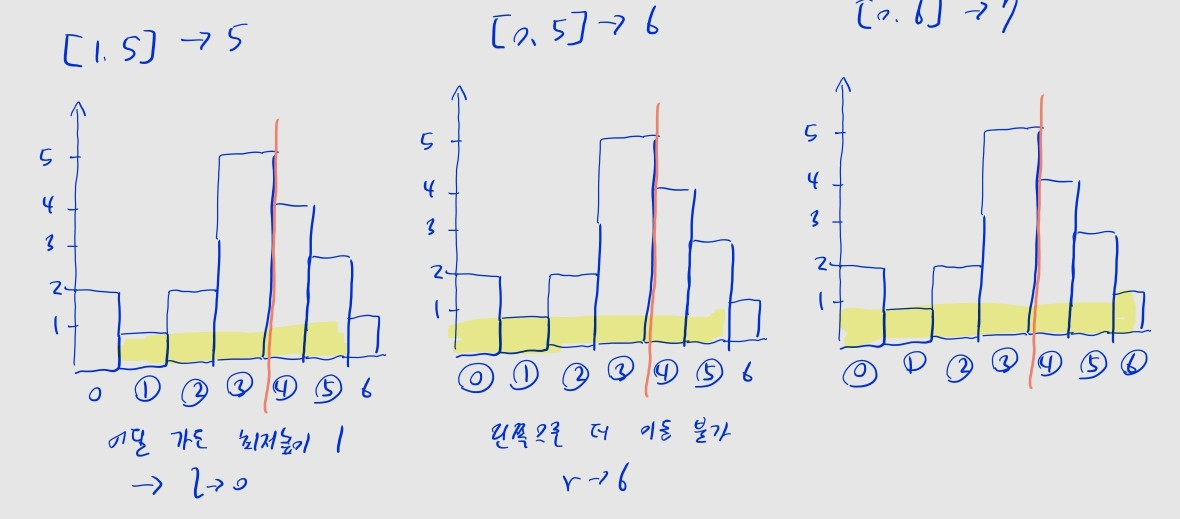
• 이후 l을 l-1로 이동해서 왼쪽 칸을 탐색하거나, r을 r+1로 이동해서 오른쪽 칸을 탐색합니다.
  • 이동을 하면 범위에 막대기 하나가 추가되어, 막대기들 중 최소 높이가 낮아질 수 있습니다.
  • 이동했을 때, height (막대기들 중 최소 높이)가 더 높게 유지되는 쪽으로 이동합니다.
  • 더 왼쪽으로 못 가면 무조건 r을, 더 오른쪽으로 못 가면 무조건 l을 이동합니다.
• 이 과정을 모든 막대기를 탐색할 때까지 반복합니다. (while True)
• 최종적으로 left, right, cross 중 최댓값을 반환하면 됩니다.

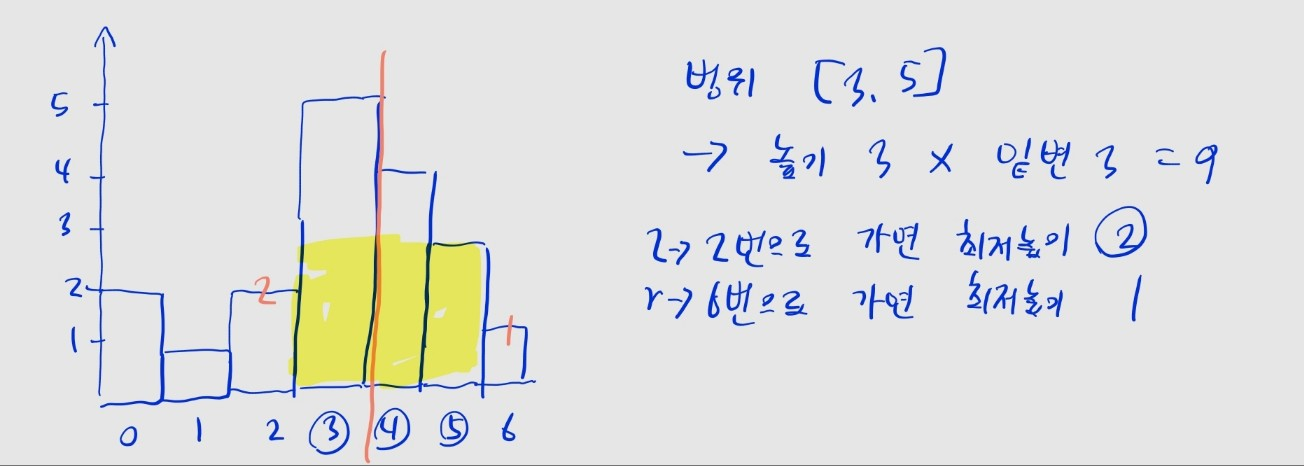
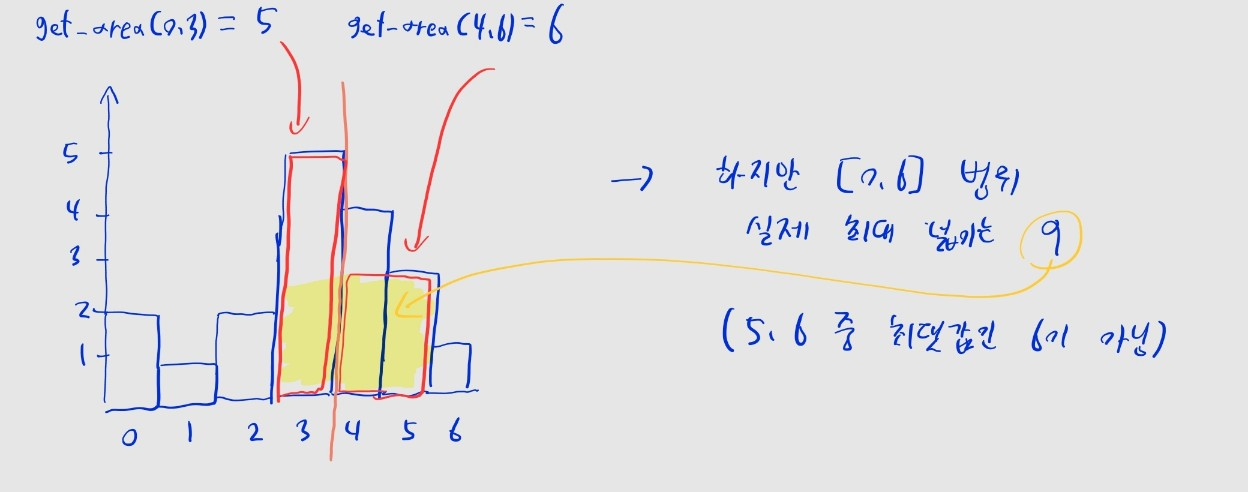
• 위 과정대로 넓이를 구하면 cross의 값은 9가 됩니다.
• 왜 굳이 이렇게 탐색하냐고요? for문 2개 이용해서 넓이의 모든 경우의 수 구하면 되지 않냐고요? 시간 초과... 하하...

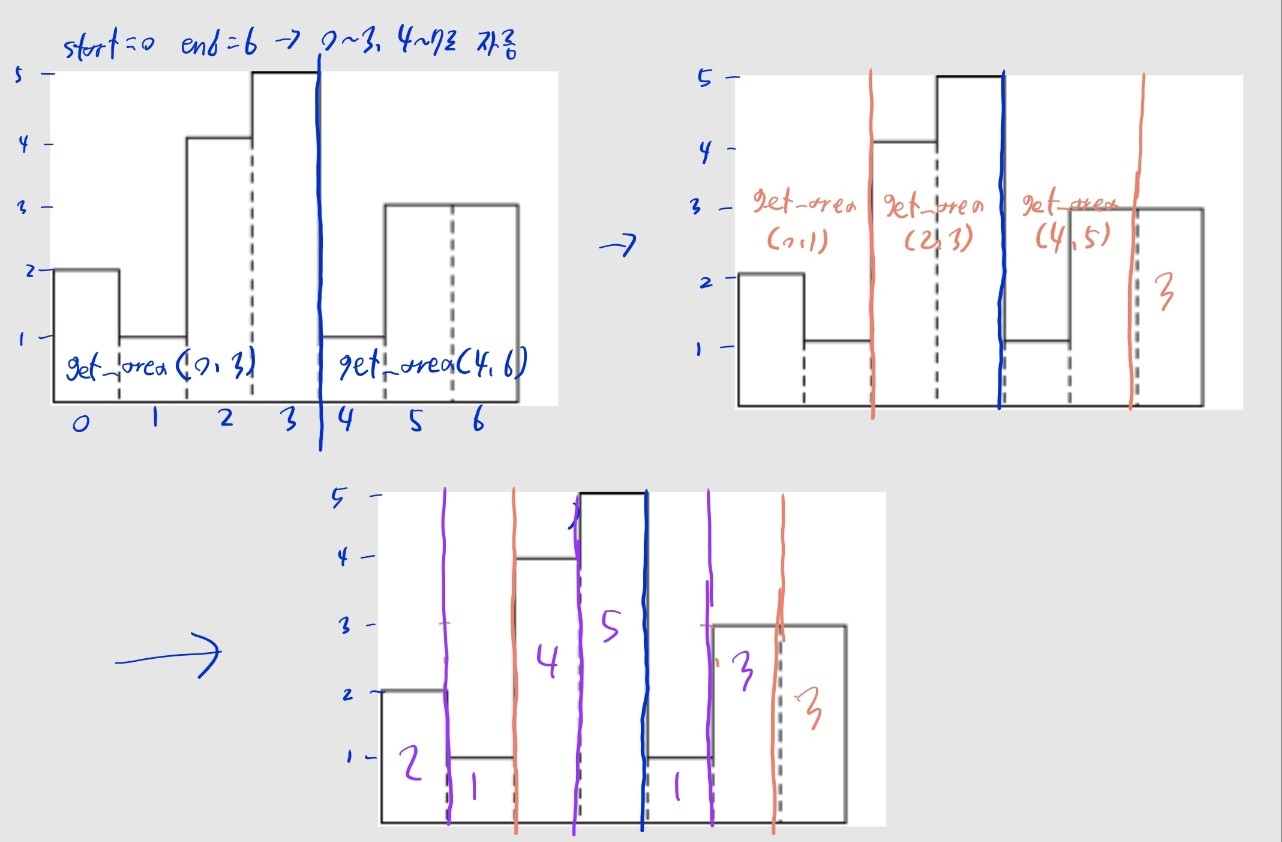
전체 동작 과정

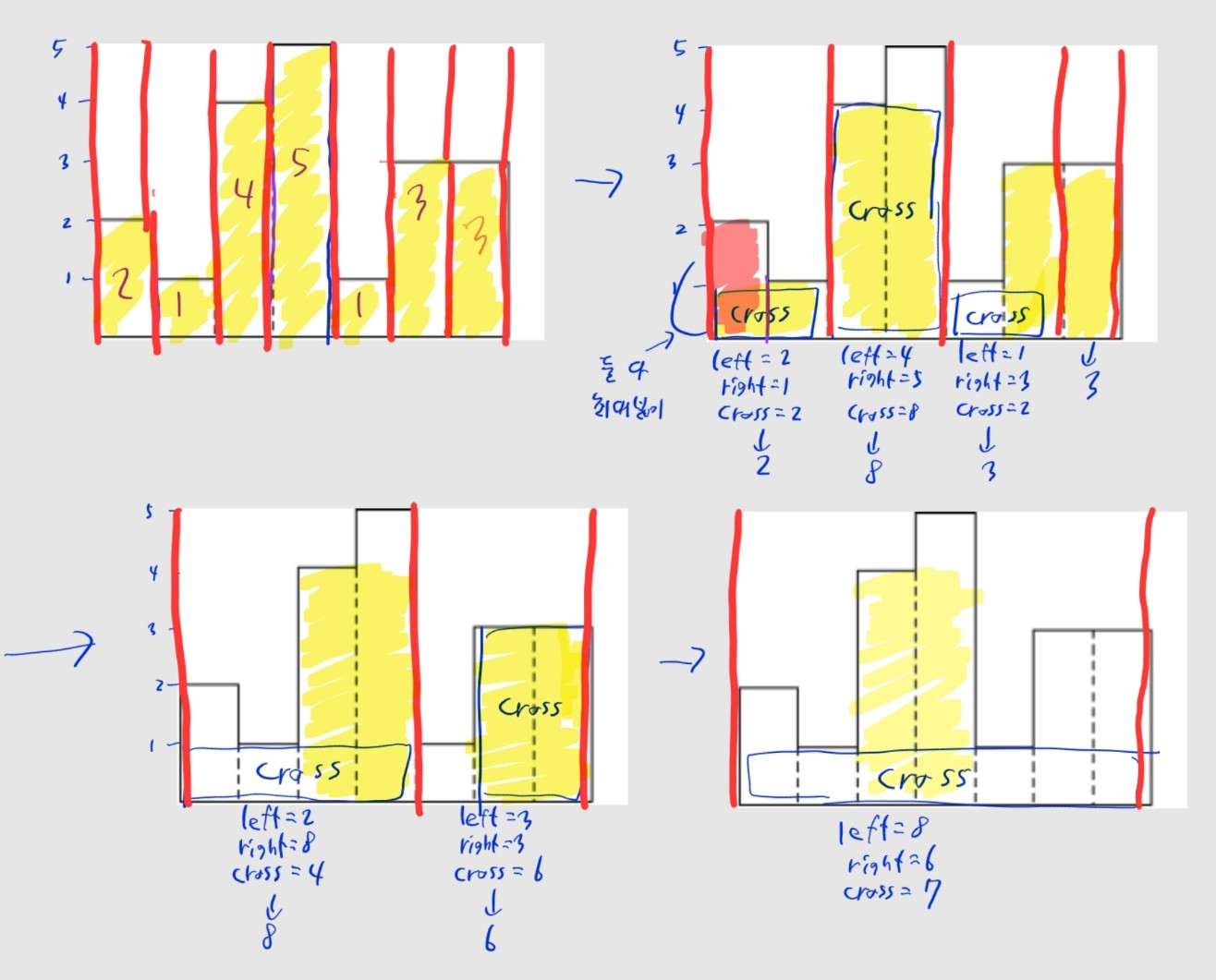
• 주인장이 실성을 해 풀이를 날림으로 쓴 감이 있어, 대신 동작 과정을 보여드리겠습니다.
• 각 재귀함수에서 계산된 최고 넓이는 노란색으로, 각 재귀함수 내 가로지르는 최대 영역(cross)은 파란색으로 표시했으니 참고 바랍니다.
  

풀이

# 인덱스 start부터 end까지 히스토그램의 최대넓이
def get_area(hist, start, end):
    
    # 종료조건 - 밑변의 길이가 1일 때
    if start == end:
        return hist[start]
    
    mid = (start + end) // 2
    
    # 왼쪽 영역 최댓값
    left = get_area(hist, start, mid)
    
    # 오른쪽 영역 최댓값
    right = get_area(hist, mid + 1, end)
    
    # 왼쪽, 오른쪽을 가로지르는 영역 최댓값
    l = mid
    r = mid + 1
    
    cross = 0
    height = min(hist[l], hist[r])
    
    while True:
        area = (r - l + 1) * height
        cross = max(area, cross)
        
        if l <= start and end <= r:
            break
        elif l <= start:    # j를 우측으로 이동
            height = min(height, hist[r + 1])
            r += 1
        elif end <= r:      # i를 좌측으로 이동
            height = min(height, hist[l - 1])
            l -= 1
        else:
            r_height = min(height, hist[r + 1])
            l_height = min(height, hist[l - 1])
            if l_height > r_height:
                height = l_height
                l -= 1
            else:
                height = r_height
                r += 1

    return max(left, right, cross)

while True:
    num_input = input()
    if num_input == "0":
        break
    hist = list(map(int, num_input.split()))[1:]
    print(get_area(hist, 0, len(hist) - 1))

시간 복잡도

• 히스토그램의 막대기 수가 $N$개일 때
• 전체 구간을 반씩 분할하므로, 재귀 깊이는 약 $\log N$
  • 각 재귀 깊이마다, 가로지르는 영역의 넓이를 구하기 위해 모든 막대기를 한번씩 확인, $O(N)$
• 최종 $O(N \log N)$

기억할 점

• 위 문제처럼 두 개의 인덱스 변수를 이동시켜 범위를 탐색하는 방법을 "투 포인터"라고도 부른다.