백준 / 골드 4 / 2617. 구슬 찾기

오징어게임 시즌 3 빨리 보고 싶습니다... 풀리면 숙소동에서 정주행할 예정입니다.

생각해봅시다!

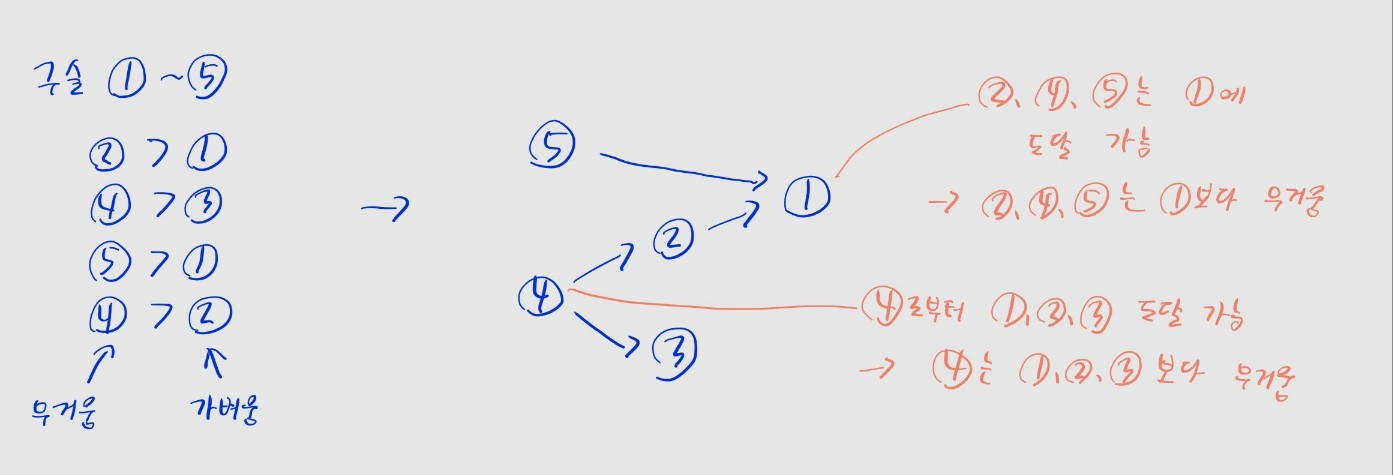
• 각 구슬을 노드로 생각하고, 무거운 구슬에서 가벼운 구슬로 간선이 존재한다고 생각합시다.
  • e.g., "구슬 2번이 구슬 1번보다 무겁다"라는 정보가 주어지면
  • 노드 2번 -> 1번으로 향하는 간선이 있다고 생각합시다.
• 이렇게 만들어진 방향성 그래프에서,
  • 노드 A에 도달할 수 있는 노드들은, 노드 A보다 무거운 구슬,
  • 노드 B로부터 도달할 수 있는 노드들는, 노드 B보다 가벼운 구슬이 됩니다.
• 즉 이러한 그래프에서, 각 노드 간 경로가 존재하는지 확인할 방법이 있음 좋겠군요.
  • 각 노드 간?? -> 여러 노드 간 경로 유무를 한 번에 파악 가능한 플로이드-워셜을 써 봅시다.

플로이드-워셜 알고리즘

• 플로이드-워셜 알고리즘은 원래 노드 쌍 간 최단 거리를 구할 때 사용하지만, 각 노드 쌍간 경로가 존재하는지 역시 확인할 수 있습니다.
  • 이를 통해, 각 노드에 도달할 수 있는 노드 수 / 각 노드로부터 도달할 수 있는 노드 수를 계산할 수 있습니다.
  • 즉 각 노드보다 무거운 구슬 수와, 각 노드보다 가벼운 구슬 수를 계산할 수 있습니다.

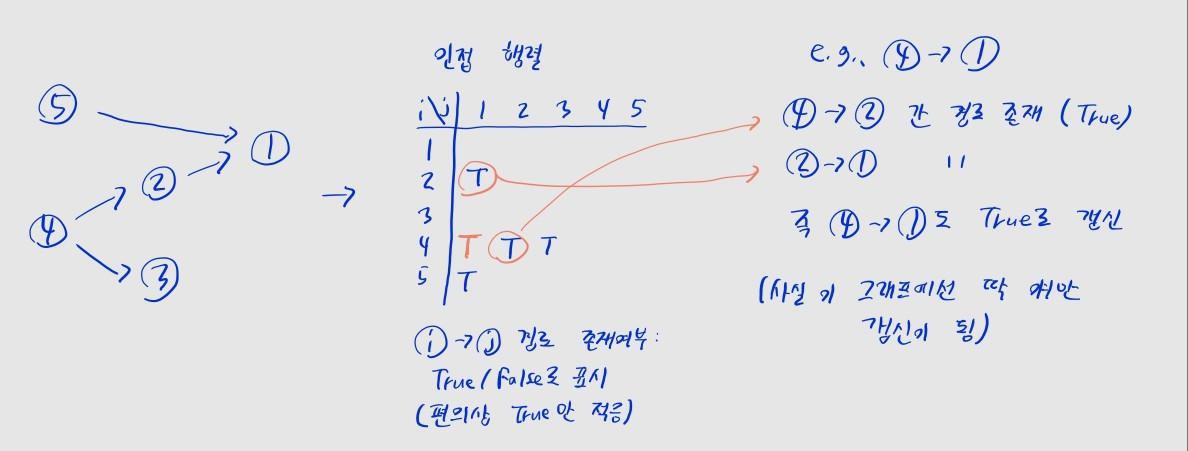
• 단 실제 경로를 계산하지는 않고, 경로가 존재하는지만 인접 행렬로 True/False로 확인하면 됩니다.
  • 임의의 노드 k에 대해 노드 i -> k로 향하는 경로와, 노드 k -> j로 향하는 경로가 모두 존재하면
  • i -> j로도 이동할 수 있다고 간주합니다.
• 예를 들어, 위 그래프에서 4번에서 1번으로 향하는 경로가 있는지 확인할 때
  • 4->2 방향의 경로가 있고, 2->1 방향의 경로가 있으니
  • 4->1 역시 경로가 존재한다고 볼 수 있습니다.

import sys
N, M = map(int, input().split())
input = sys.stdin.readline

# 인접 행렬 표현
# i행 j열 -> 노드 i에서 j로 가는 경로가 존재하는지 True, False로 저장
graph = [[False] * (N + 1) for _ in range(N + 1)]

# 거리 비교 정보를 통해 간선 표시
for _ in range(M):
    heavy, light = map(int, input().split())
    graph[heavy][light] = True 

# 플로이드 워셜: 경로가 존재할 시 갱신 (i->k 경로, k->j 경로가 모두 존재할 때)
for k in range(1, N + 1):
    for i in range(1, N + 1):
        for j in range(1, N + 1):
            if not graph[i][j]:    # 이미 경로가 존재할 시 확인할 필요 없음
                graph[i][j] = graph[i][k] and graph[k][j]

• 플로이드-워셜 이후엔 위와 같이 i행 j열에 노드 i -> j로 이동 가능한지를 True, False로 표시한 행렬을 구할 수 있습니다.

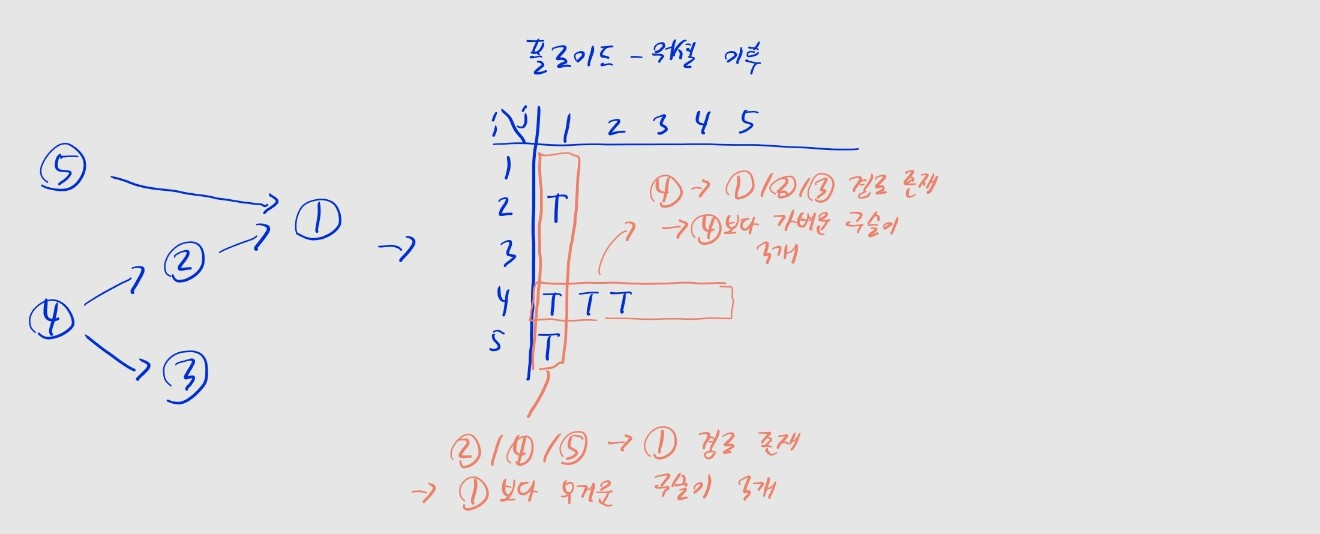
• 무거운 구슬 -> 가벼운 구슬 방향으로 이동 가능하다는 점을 다시 기억합시다.
• 이때 i행의 True 개수는, 노드 i로부터 도달할 수 있는 노드의 개수입니다.
  • 즉 i보다 가벼운 구슬이 몇 개인지를 뜻합니다.
• 또한 j열의 True 개수는, 노드 j에 도달할 수 있는 노드의 개수입니다.
  • 즉 j보다 무거운 구슬이 몇 개인지를 뜻합니다.보다 무거운 구슬이 몇 개인지를 뜻합니다.
• 구슬이 $N$개일 때 가운데 순서는 $(N + 1) // 2$번째 입니다.
  • 즉 자신보다 가볍거나 무거운 구슬이 $(N + 1) // 2$개 이상이면 해당 구슬은 가운데에 올 수 없습니다.

answer = 0
for i in range(1, N + 1):
    # 더 가벼운 게 몇 개?
    row_check = sum(graph[i][j] for j in range(1, N + 1))
    
    # 더 무거운 게 몇 개?
    col_check = sum(graph[j][i] for j in range(1, N + 1))
    
    if row_check >= (N + 1) // 2 or col_check >= (N + 1) // 2:
        answer += 1

print(answer)

풀이

import sys
N, M = map(int, input().split())
input = sys.stdin.readline

# 인접 행렬 표현
# i행 j열 -> 노드 i에서 j로 가는 경로가 존재하는지 True, False로 저장
graph = [[False] * (N + 1) for _ in range(N + 1)]

# 거리 비교 정보를 통해 간선 표시
for _ in range(M):
    heavy, light = map(int, input().split())
    graph[heavy][light] = True 

# 플로이드 워셜: 경로가 존재할 시 갱신 (i->k 경로, k->j 경로가 모두 존재할 때)
for k in range(1, N + 1):
    for i in range(1, N + 1):
        for j in range(1, N + 1):
            if not graph[i][j]:    # 이미 경로가 존재할 시 확인할 필요 없음
                graph[i][j] = graph[i][k] and graph[k][j]
            
answer = 0
for i in range(1, N + 1):
    # 더 가벼운 게 몇 개?
    row_check = sum(graph[i][j] for j in range(1, N + 1))
    
    # 더 무거운 게 몇 개?
    col_check = sum(graph[j][i] for j in range(1, N + 1))
    
    if row_check >= (N + 1) // 2 or col_check >= (N + 1) // 2:
        answer += 1

print(answer)

시간 복잡도

• 구슬의 수가 $N$개일 때, 플로이드 워셜 알고리즘을 사용했으므로 $O(N^3)$
• $N \leq 99$이므로, 1초 만에 가능

기억할 점

• 모든 요소 / 성분 / 대상 사이 관계를 한 번에 알고 싶을 땐 플로이드 워셜을 사용한다. 다만 시간 복잡도가 높으니까, 사용하기 전에 문제의 크기는 반드시 고려한다.