백준 / 골드 4 / 3055. 탈출

생각해봅시다!

• 매 분마다 인접한 칸으로 물이 찬다는 점이 중요합니다.
• 고슴도치는 현재 물이 찬 칸과, 1분 후에 물이 찰 칸으로는 이동할 수 없습니다.
• 즉 시간이 흐르면서 지나갈 수 없는 칸이 증가한다는 점을 잘 구현해야 합니다.
• 풀이방법이 여러 개 있겠지만, 저는 이렇게 접근했습니다.
  • (1단계): 각 칸에 언제 물이 차는지 계산한다.
  • (2단계): 앞선 물이 찰 시간 정보를 활용하여, 고슴도치가 비버의 굴로 이동하는데 필요한 시간을 구한다.

입력

from collections import deque
import sys
input = sys.stdin.readline

R, C = map(int, input().split())
graph = []

for _ in range(R):
    graph.append(list(input()))
    
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]

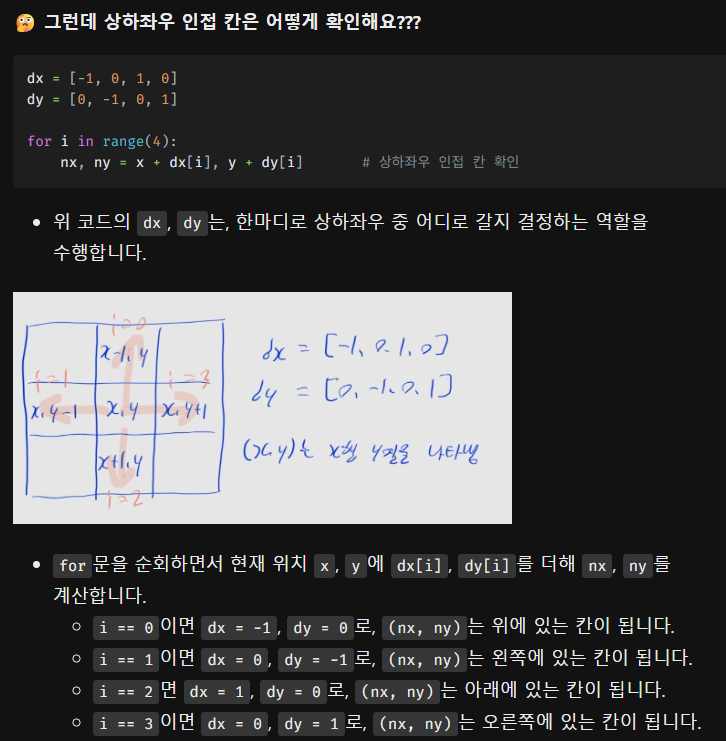
• 이제는 많이 익숙해지셨을 2차원 배열 문제입니다~
• dx, dy 리스트로 상하좌우 이동 하는 것도 익숙해지셨으리라 믿습니다...

1단계. 각 칸에 언제 물이 찰지 계산

# N초부터 물이 차 있음
# 물이 차지 않은 칸은 INF로 초기화
INF = float('inf')
water = [[INF] * C for _ in range(R)]
water_queue = deque()

for x in range(R):
    for y in range(C):
        if graph[x][y] == "S":
            sx, sy = x, y       # 고슴도치 시작 좌표
        elif graph[x][y] == "*":	# 처음부터 물이 차 있는 칸
            water_queue.append((x, y))
            water[x][y] = 1			# 1분째부터 차 있음

• BFS를 통해 물을 채울 거니까 큐를 사용하겠습니다.
• water[i][j]에는 i행 j열 칸에 물이 시작하는 시간을 저장할 겁니다.
  • 물이 차지 않는 칸은 무한대 값으로 초기화합니다.
• 고슴도치의 이동이 시작되는 좌표 ("S")는 미리 기록해 둡니다.
• 물이 존재하는 좌표("*")는 큐에 삽입하고, 1분째부터 물이 차 있다고 표시합니다.

# water 채우기 위해 BFS
while water_queue:
    x, y = water_queue.popleft()
    for i in range(4):
        # 상하좌우 인접 칸
        nx, ny = x + dx[i], y + dy[i]
        # 좌표 범위를 안 벗어나는가?
        if 0 <= nx < R and 0 <= ny < C:
        	# 아직 물이 안 찬 칸인가? + 돌('X')이나 비버('D')의 굴이 아닌가?
            if water[nx][ny] == INF and graph[nx][ny] not in {"X", "D"}:
            	# 현재 칸보다 1분 후에 물이 참
                water[nx][ny] = water[x][y] + 1
                water_queue.append((nx, ny))

• BFS로 인접 칸이 돌(X)이나 비버의 굴(D)이 아니고, 아직 물이 차지 않았다면(water[nx][ny] == INF), 물이 차는 시간을 현재 칸의 물 시간 + 1로 갱신합니다.

2단계. 고슴도치의 이동 시간 계산

# 각 칸의 고슴도치 도착 여부
visited = [[False] * C for _ in range(R)] 

# 고슴도치의 이동
def move_dochi():

	# 고슴도치의 (행 위치, 열 위치, 경과 시간(분))
    dochi_queue = deque([(sx, sy, 1)])
    visited[sx][sy] = True
    while dochi_queue:
        x, y, time = dochi_queue.popleft()
        for i in range(4):
        	# 상하좌우 인접 칸
            nx, ny = x + dx[i], y + dy[i]
            
            # 격좌 범위를 안 벗어나는가?
            if 0 <= nx < R and 0 <= ny < C:
            	# 아직 안 방문했는가? 돌이 없는가? 물로 차 있거나 찰 예정이 아닌가?
                if not visited[nx][ny] and graph[nx][ny] != "X" and water[nx][ny] > time + 1:
                	# 비버의 굴에 도착하면, 현재 시간을 반환
                    if graph[nx][ny] == "D":
                        return time
                    visited[nx][ny] = True
                    dochi_queue.append((nx, ny, time + 1))
    
    # 비버의 굴에 도착하기 전에, 이동할 칸이 없어 BFS가 끝난 경우
    return "KAKTUS"

print(move_dochi())       

• 이제 각 칸에 물이 언제 차는지를 water 리스트에 저장해 두었으므로, 이 정보를 바탕으로 고슴도치를 움직일 수 있습니다.
• 고슴도치의 움직임 역시 BFS로 구현했습니다. 큐에는 (x좌표, y좌표, 경과시간) 꼴로 삽입해서 경과시간 흐름을 관리합니다.
• 움직일 칸을 확인할 때, 아직 방문하지 않았는지(if not visited[nx][ny], 돌(X)이 없는지 확인합니다.
• 또한 물이 이미 찾거나, 1분 후에 찰 예정이 아닌 칸만 확인합니다.
  • 1분 후에 찰 예정인 칸으로도 이동할 수 없으므로, water[nx][ny] > time + 1로 조건을 설정합니다.
• 비버의 굴(D)에 도착하면 경과 시간을 반환합니다.
• 모든 가능한 이동 경로를 탐색했지만 비버의 굴에 도달하지 못해 BFS가 끝난 경우 "KAKTUS"를 반환합니다.

풀이

from collections import deque
import sys
input = sys.stdin.readline

R, C = map(int, input().split())
graph = []

for _ in range(R):
    graph.append(list(input()))
    
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]

# N초부터 물이 차 있음
# 물이 차지 않은 칸은 INF로 초기화
INF = float('inf')
water = [[INF] * C for _ in range(R)]
water_queue = deque()

for x in range(R):
    for y in range(C):
        if graph[x][y] == "S":
            sx, sy = x, y       # 고슴도치 시작 좌표
        elif graph[x][y] == "*":	# 처음부터 물이 차 있는 칸
            water_queue.append((x, y))
            water[x][y] = 1			# 1분째부터 차 있음

# water 채우기 위해 BFS
while water_queue:
    x, y = water_queue.popleft()
    for i in range(4):
        # 상하좌우 인접 칸
        nx, ny = x + dx[i], y + dy[i]
        # 좌표 범위를 안 벗어나는가?
        if 0 <= nx < R and 0 <= ny < C:
        	# 아직 물이 안 찬 칸인가? + 돌('X')이나 비버('D')의 굴이 아닌가?
            if water[nx][ny] == INF and graph[nx][ny] not in {"X", "D"}:
            	# 현재 칸보다 1분 후에 물이 참
                water[nx][ny] = water[x][y] + 1
                water_queue.append((nx, ny))

# 각 칸의 고슴도치 도착 여부
visited = [[False] * C for _ in range(R)] 

# 고슴도치의 이동
def move_dochi():

	# 고슴도치의 (행 위치, 열 위치, 경과 시간(분))
    dochi_queue = deque([(sx, sy, 1)])
    visited[sx][sy] = True
    while dochi_queue:
        x, y, time = dochi_queue.popleft()
        for i in range(4):
        	# 상하좌우 인접 칸
            nx, ny = x + dx[i], y + dy[i]
            
            # 격좌 범위를 안 벗어나는가?
            if 0 <= nx < R and 0 <= ny < C:
            	# 아직 안 방문했는가? 돌이 없는가? 물로 차 있거나 찰 예정이 아닌가?
                if not visited[nx][ny] and graph[nx][ny] != "X" and water[nx][ny] > time + 1:
                	# 비버의 굴에 도착하면, 현재 시간을 반환
                    if graph[nx][ny] == "D":
                        return time
                    visited[nx][ny] = True
                    dochi_queue.append((nx, ny, time + 1))
    
    # 비버의 굴에 도착하기 전에, 이동할 칸이 없어 BFS가 끝난 경우
    return "KAKTUS"

print(move_dochi()) 

시간 복잡도

• 지도를 $R$행 $C$열로 둘 때, 두 번의 BFS로 모든 칸을 순회하므로 $O(R \times C)$.
• $R \leq 50, C \leq 50$이므로 칸 수는 최대 $2500$개에 불과. 시간초과가 뜰 일은 없음.

기억할 점

• 고슴도치는 귀엽다.