백준 / 골드 4 / 8983. 사냥꾼

국카스텐 - 사냥꾼
들으면서 보시면 집중이 더 잘 될겁니다

생각해봅시다!!

• 사대의 위치와 동물들의 위치가 주어졌을 때, 잡을 수 있는 동물의 수를 세면 됩니다.
• 이때 어떤 동물이 하나 이상의 사대로부터 사정거리 내 있으면, 그 동물은 잡을 수 있습니다.
• 그러므로 사대를 하나씩 확인하면서, 쏠 수 있는 동물들을 확인하기보단...
  • 동물을 하나씩 확인하면서, 그 동물을 맞출 수 있는 사대가 하나라도 존재하는지 확인하는 게 효율적이겠죠.
  • 동물을 잡을 수 있는 사대가 몇 개인지는 상관없습니다. 단 하나만 존재해도 됩니다!!

사정거리 계산

• 동물의 위치를 $(x, y)$, 사정거리를 $L$로 둡시다.
  • 사대는 $y = 0$에, 모든 동물은 $y \geq 1$에 존재한다는 점을 기억합시다.
• 해당 동물을 구할 수 있는 사대의 범위를 구할 건데, 사대의 위치는 $(a, 0)$으로 두겠습니다.

식 세우기

• 사대와 동물 간의 거리는 $|a - x| + y$이며, 이 값은 사정거리 $L$ 이하여야 합니다.
  • $|a - x| + y \leq L$
  • $|a - x| \leq L - y$
  • $-L + y \leq a - x \leq L - y$
  • $-L + x + y \leq a \leq L + x - y$
• 즉 동물의 위치가 $(x, y)$일 때, $-L + x + y \leq a \leq L + x - y$ 사이에 사대가 1개라도 있으면 그 동물을 맞출 수 있습니다.

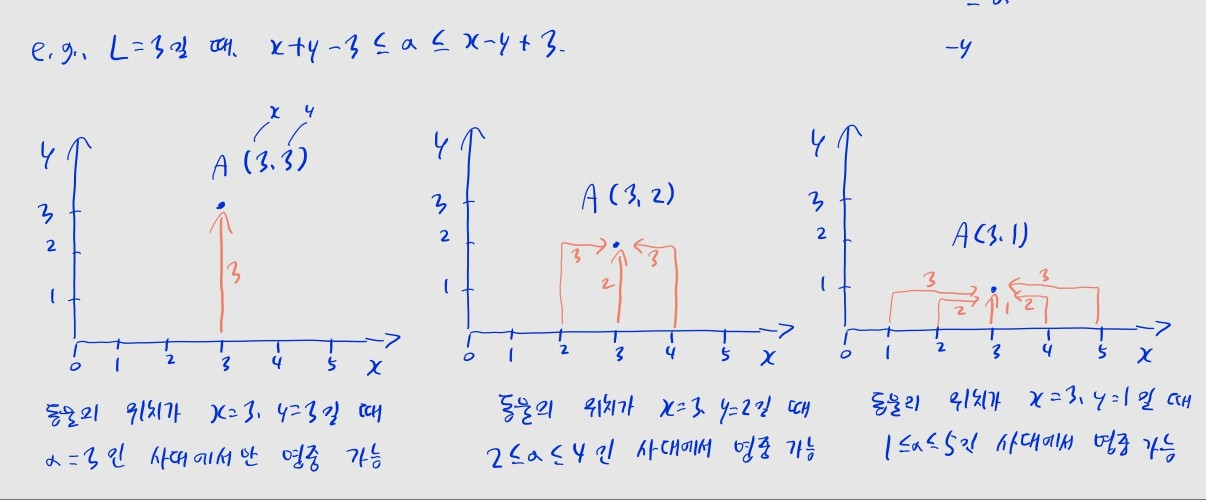
예제

• e.g., 사정거리가 $3$일 때, $x + y - 3 \leq a \leq x - y + 3$ 사이에 사대가 있어야 합니다. 자세한 건 아래 그림을 보세요
  

동물을 쏠 수 있는 사대 찾기

• 그러면 이제 동물의 좌표 (x, y)가 주어질 때, $-L + x + y \leq a \leq L + x - y$ 사이에 위치한 사대가 있는지 확인하면 됩니다.
• 하지만 각 사대가 범위 안에 들어오는지 일일이 체크하면...
  • 사대의 수가 $M$개일 때 $O(M)$... 사대의 수 $M$은 $M \leq 100,000$...
  • 더군다나 동물의 수가 $N \leq 100,000$개...
  • $O(N \times M)$.. 대충 시간초과가 뜨는 소리가 들리죠?
• 앗? 탐색을 하는데 시간이 너무 오래 걸린다? 그러면 빠른 이분 탐색을 이용해봅시다!

import sys
input = sys.stdin.readline

# 사대의 수, 동물의 수, 사정거리
M, N, L = map(int, input().split())

# 사대의 위치
sadaes = list(map(int, input().split()))
sadaes.sort()

# 이분탐색: 쏠 수 있는 사대가 있나요?
def binary_search(fire_a, fire_b): 
    l = 0
    r = M - 1
    
    while l <= r:
        m = (l + r) // 2
        if fire_a <= sadaes[m] <= fire_b:
            return True
        elif sadaes[m] < fire_a:
            l = m + 1
        else:   # fire_b < sadaes[m]
            r = m - 1
    return False

• binary_search 함수는 fire_a <= (사대) <= fire_b 범위에 위치한 사대가 있는지, 이분 탐색을 합니다.
• 우선 정상적인 이분 탐색을 위해, 사대의 위치가 담긴 리스트 sadaes을 정렬해야 합니다.
  • 사대 영어로 뭐라고 하는지 찾기 귀찮았어요 이해 좀...
• 그리고 이분 탐색을 진행하며, 찾은 사대의 위치에 따라 탐색 범위를 좁힙니다.
  • 사대의 위치가 fire_a, fire_b 사이에 있는 경우, 바로 True를 반환합니다.
  • 사대의 위치가 fire_a 이전인 경우, 더 오른쪽을 찾아봐야 하니 l = m + 1로 설정합니다.
  • 사대의 위치가 fire_b 이후인 경우, 더 왼쪽을 찾아봐야 하니 r = m - 1로 설정합니다.
  • 끝내 못 찾으면 False를 반환합니다.
• 이분 탐색의 시간 복잡도는, 사대의 수가 $M$개일 때 $(O \log M)$입니다.

동물 수 세기

# 동물 수 세기
count = 0
for _ in range(N):
    x, y = map(int, input().split())
    fire_a = max(sadaes[0], -L + x + y)      
    fire_b = min(sadaes[-1], L + x - y)
    
    # 해당 동물을 쏠 수 있는 사대가 있는지 확인
    if binary_search(fire_a, fire_b):
        count += 1
        
print(count)

• 이제 각 동물의 좌표 (x, y)가 주어지면, 해당 동물을 쏠 수 있는 사대가 fire_a, fire_b범위 내 존재하는지 이분 탐색으로 확인하면 됩니다.
  • $-L + x + y \leq a \leq L + x - y$ 였죠?
  • 단 여기선 fire_a = max(sadaes[0], -L + x + y)), fire_b = min(sadaes[-1], L + x - y)로 설정했습니다.
  • 사대 위치를 담은 리스트를 정렬했던 거 기억하시죠? 그러니까 sades[0]는 맨 왼쪽 사대의 위치, sadaes[-1]은 맨 오른쪽 사대의 위치가 됩니다.
  • 굳이 맨 왼쪽 사대 이전 위치나, 맨 오른쪽 사대 이후 위치는 찾아볼 필요가 없겠죠?
• 범위 내 사대가 존재해서 True를 반환하므로 count가 1 증가합니다. 최종 count가 정답이 되겠습니다.

풀이

import sys
input = sys.stdin.readline

# 사대의 수, 동물의 수, 사정거리
M, N, L = map(int, input().split())

# 사대의 위치
sadaes = list(map(int, input().split()))

# 이분탐색을 위한 정렬
sadaes.sort()

# 이분탐색
# fire_a <= (사대) <= fire_b 범위에 사대가 있나요?
def binary_search(fire_a, fire_b): 
    l = 0
    r = M - 1
    
    while l <= r:
        m = (l + r) // 2
        # 사대가 범위 내에 있음
        if fire_a <= sadaes[m] <= fire_b:
            return True
        
        # 사대가 범위 왼쪽에 있음
        elif sadaes[m] < fire_a:
            l = m + 1
            
        # 사대가 범위 오른쪽에 있음
        else:
            r = m - 1
    return False

# 동물 수 세기
count = 0
for _ in range(N):
    x, y = map(int, input().split())
    fire_a = max(sadaes[0], -L + x + y)
    fire_b = min(sadaes[-1], L + x - y)
    
    # 해당 동물을 쏠 수 있는 사대가 있는지 확인
    if binary_search(fire_a, fire_b):
        count += 1
        
print(count)      

시간 복잡도

• $M$개의 사대 정렬 -> $O(M \log M)$
• $N$개의 동물에 대해 각각 시간 복잡도 $O(\log M)$의 이분탐색 진행 -> $O(N \log M)$
• 최종 $O((M + N) \log M)$
• $M \leq 100,000$, $N \leq 100,000$... 차피 $O(A \log A)$꼴이므로, 이정도면 1초만에 통과 가능

기억할 점

• 이분 탐색은 빠르다. 한 문제에서 여러 번 이분 탐색을 사용하는 것에 부담을 갖지 말자.