선형 자료구조는 자료를 순차적으로 나열한 형태이고, 많이 사용된다.

• 배열
• 연결 리스트
• 스택/큐

이와 반대로 비선형 자료구조는 하나의 자료 뒤에 다수의 자료가 올 수 있는 형태이다. 예를 들어 파일 탐색, 길 찾기 등은 일대일관계가 아니므로 비선형 자료구조를 활용해야 한다.

• 트리
• 그래프

이번 포스트에서는 트리, 우선순위 큐, 그래프에 대해 살펴본다.

---

트리

• 계층적 구조를 갖는 데이터를 표현하기 위한 자료구조

• 노드 : 데이터를 표현

• 간선 : 노드의 계층 구조를 표현하기 위해 사용

노드, 간선은 그래프에서도 활용되는 개념이다. 연결리스트는 앞뒤로만 연결할 수 있기 때문에 이렇게 트리처럼 여러 항목을 동시에 가리키지는 못한다!

트리는 양파같다. 까도까도 나오기 때문! 그래서 재귀함수와 잘 어울린다.

우선순위 큐, 탐색 용도의 레드블랙 트리로 활용되므로 아래처럼 기초적인 것은 잘 쓰이지 않는다.

#include <iostream>
using namespace std;
#include <vector>

class Node
{
public:
	Node(const char* data) : data() {}
public:
	const char* data;
    vector<Node*> children;
};

Node* CreateTree()
{
	Node* root = new Node("우리 동아리");
    {
    	Node node = new Node("컴퓨터공학부");
        root->childrem.push_back(node);
        {
        	Node* leaf = new Node("모바일");
            node->children.push_back(leaf);
        }
        {
        	Node* leaf = new Node("백엔드");
            node->children.push_back(leaf);
        }
        {
        	Node* leaf = new Node("프론트엔드");
            node->children.push_back(leaf);
        }
    }
    {
    	Node node = new Node("디자인학부");
        root->childrem.push_back(node);
        {
        	Node* leaf = new Node("2D 일러스트");
            node->children.push_back(leaf);
        }
        {
        	Node* leaf = new Node("3D 아트");
            node->children.push_back(leaf);
        }
        {
        	Node* leaf = new Node("영상");
            node->children.push_back(leaf);
        }
    }
    {
    	Node node = new Node("기타학부");
        root->childrem.push_back(node);
        {
        	Node* leaf = new Node("기획");
            node->children.push_back(leaf);
        }
        {
        	Node* leaf = new Node("회계");
            node->children.push_back(leaf);
        }
    }
    
    return root;
}

// 깊이 (depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 개수
void PrintTree(Node* root, int depth = 0)
{
	for (int i=0; i<depth; i++)
    	cout << "-";

	cout << root->data << endl;
    int size = root->children.size();
    for (int i=0; i<size; i++) // 간접적인 기저사항 !!!
    {
    	Node* node = root->children[i];
        PrintTree(node, depth + 1); // 재귀 함수 !!!
    }
}

// 높이
int GetHeight(Node* root)
{
	int ret = 1;
    int size = root->children.size();
    for (int i=0; i<size; i++)
    {
    	Node* node = root->children[i];
        int h = GetHeight(node) + 1;
        
        if (ret < h)
        	ret = h;
    }
    
    return ret;
}

int main()
{
	Node* root = CreateTree();
    
    PrintTree(root);

	int h = GetHeight(root);
}

---

우선순위 큐

시간복잡도는 아래 코드 참고 ⭐️

왜 필요한가?

• 가장 좋은 케이스 하나 (최솟값 혹은 최댓값) 를 추출해야할 때 유용하다.

이진 트리

• 각 노드가 최대 두 개의 자식 노드를 가지는 트리

이진 검색 트리

• 왼쪽으로 가면 현재값보다 작고,
• 오른쪽으로 가면 현재값보다 크다.
• 검색이 빠를 수 있다는 이점이 있다.

이진 검색 트리의 문제 ✔️

• 그냥 막~ 추가하면, 한쪽으로 기울어져서 균형이 깨지고

  • 연결리스트와 다를 것이 없어져서
  • 탐색이 O(N)이 될 수 있다.

• 트리 재배치를 통해 균형을 유지하는 것이 과제이다. (AVL, Red-Black)

힙 트리 ⭐️

• [1 법칙]

  • 부모 노드가 가진 값은 항상 자식 노드가 가진 값보다 크다.
  • 왼쪽, 오른쪽 값 중 어떤 값이 더 커야 하는지는 정해져있지 않다.

• [2 법칙]

  • 노드 개수를 알면, 트리 구조는 무조건 확정할 수 있다.

힙 트리 구조

• 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있다. (완전 이진 트리)

• 마지막 레벨에 노드가 있을 때는, 항상 왼쪽부터 순서대로 채워야 한다.

힙 트리 구현

• 배열(vector) 을 이용해서 힙 구조를 바로 표현할 수 있다.
  1) i 번 노드의 왼쪽 자식은 [(2*i) + 1]번
  2) i 번 노드의 오른쪽 자식은 [(2*i) + 2]번
  3) i 번 노드의 부모는 [(i-1) / 2]번
  
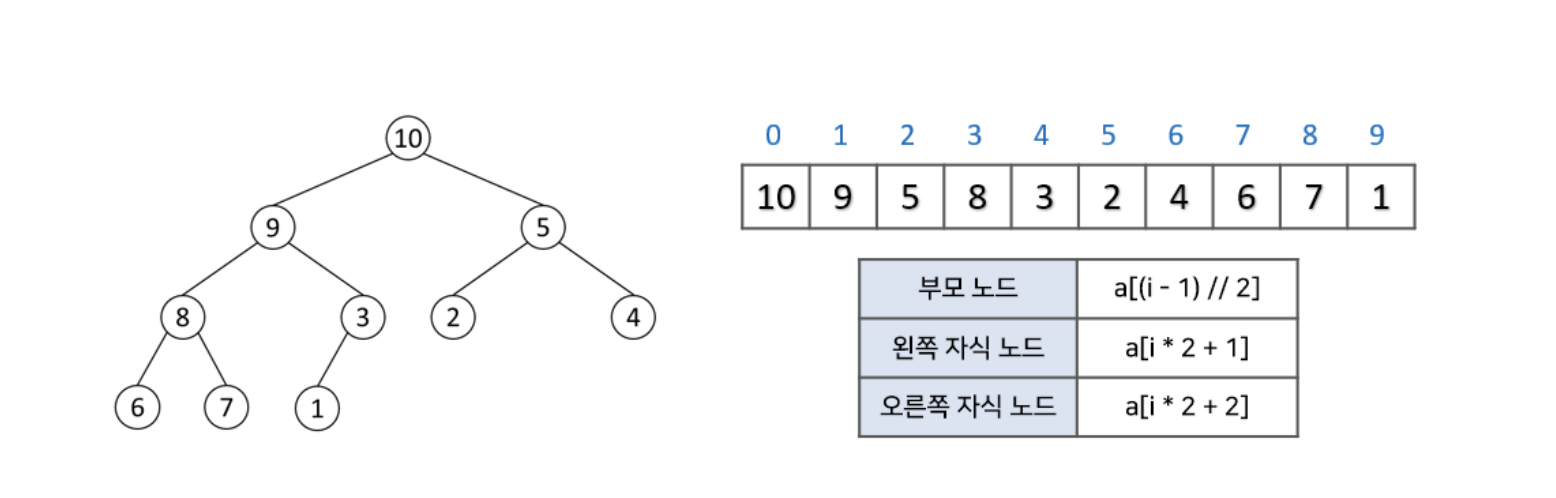
  이미지 출처

힙 트리에서 임의의 값을 추가하기

• [2 법칙] 으로 일단 마지막에 추가

• [1 법칙] 으로 도장깨기 (쿠데타 or 실패)

힙 트리에서 최대값 꺼내기

• 힙 트리 특성상 최대값은 무조건 루트 노드에 있는 값이다

• 최댓값 (루트노드) 을 먼저 제거한다

• [2 법칙] 으로, 제일 마지막에 위치한 데이터를 루트로 옮긴다

• 역 도장 깨기를 시작한다

우선순위 큐를 구현한 아래 코드를 보며 자세히 살펴보자!

#include <iostream>
using namespace std;
#include <vector>
#include <queue>

template<typename T, typename Predicate = less<T>>
class PriorityQueue
{
public:
	// O(logN) 트리의 높이에 의존적이기 때문이다
    /* 삽입, 재배치 */
	void push(const T& data)
    {
    	// 우선 힙 구조부터 맞춰준다
        _heap.push_back(data);
        
        // 도장깨기 시작
        int now = static_cast<int>(_heap.size()) - 1; // 마지막 인덱스
        
        // 루트 노드까지
        while (now > 0)
        {
        	// 부모 노드와 비교해서 더 작으면 패배
        	int next = (now - 1) / 2; // next 는 now 의 부모 노드
            // if (_heap[now] < _heap[next])
            // break;
            if (_predicate(_heap[now], _heap[next]))
            	break;
                
            // 데이터 교체
            ::swap(_heap[now], _heap[next]);
            // 현재 노드의 인덱스를 부모 노드의 인덱스로 업데이트
            now = next;
        }
    }
    
    // O(logN) 트리의 높이에 의존적이기 때문이다
    /* 최댓값 추출, 그 다음 최댓값을 [0]에 놓기 위해 재배치 */
    void pop()
    {
    	_heap[0] = _heap.back(); // 마지막 데이터를 맨 앞에 넣어주고
        _heap.pop_back(); // 마지막을 제거
        
        int now = 0; // 꼭대기부터 내려온다
        
        while(true)
        {
        	int left = 2 * now + 1;
            int right = 2 * now + 2;
            
            // 경우 1 : 리프에 도달한 경우.. 도망쳐!
            if (left >= (int)_heap.size())
            	break;
                
            int next = now;
            
            // 경우 2 : 왼쪽 비교
            if (_heap[next] < _heap[left])
            	next = left;
                
            // 경우 3 : 둘 중 숫자를 오른쪽과 비교
            // if (right < _heap.size() && _heap[next] < _heap[right])
            if (right < _heap.size() && _predicate(_heap[next], _heap[right]))
            	next = right;
                
            // 경우 4 : 왼쪽, 오른쪽 둘 다 현재 값보다 작으면 종료
            if (next == now)
				break;
            
            ::swap(_heap[now], _heap[next]);
            now = next;
        }
    }
    
    // O(1)
    T& top()
    {
    	return _heap[0];
    }

	// O(1)
	bool empty()
    {
    	return _heap.empty();
    }
    
private:
	vector<T> _heap;
    Predicate _pred; // 판별해주는 것 자체를 하나의 객체로 만들어준다
};

int main()
{
	vector<int> v;
    // less 이면 큰 값이 먼저 튀어나오고, greater 로 해주면 작은 값이 먼저 튀어나와요 (방향성)
    PriorityQueue<int, vector<int>, less<int>> pq; 
    
    pq.push(10);
    pq.push(40);
    pq.push(30);
    pq.push(50);
    pq.push(20);
    
    int value = pq.top();
    pq.pop();
}

now = next 를 왜 해주는 것일까?

• 힙은 각 노드의 값이 자식 노드보다 작은 최소 힙(Min Heap) 또는 각 노드의 값이 자식 노드보다 큰 최대 힙(Max Heap)으로 구성된다. 따라서, 새로운 요소를 추가한 후에도 힙의 특성을 유지하기 위해 부모 노드와의 비교 및 교환 작업이 필요하다.

위 코드에서 break 를 하게 되면 어떤 반복문을 빠져나오는 것일까?

• break 문은 현재 실행 중인 가장 가까운 반복문을 빠져나오게 된다.
  위 코드에서는 while 반복문을 빠져나온다.

거꾸로 하고 싶다면?

• predicate 또는 - 로 음수 처리

---

그래프

트리가 그래프의 일종이다.
그래프는 트리와 달리 딱히 계층 구조는 없고 수평적인 관계이다.

그래프란 현실 세계의 사물이나 추상적인 개념 간의 연결 관계를 표현한다.

• 정점: 데이터를 표현 (사물, 개념 등)
• 간선: 정점들을 연결하는데 사용

가중치 그래프 (weighted graph)

• 간선에 수치를 줘서 비용이나 가치를 부여할 수 있다.
• 단방향, 양방향 모두 가능하다.

게임에서는 그래프를 언제 이용할까?

• 맵에서 길찾기로 제일 많이 쓰인다

아래처럼 만들면 직관적이지만 탐색 속도가 느리고 복잡해서 잘 쓰이지 않는다.

#include <iostream>
using namespace std;
#include <vector>
#include <queue>

void CreateGraph_1()
{
	struct Vertex
    {
    	vector<Vector> edges; // 다른 Vertex 객체들의 주소를 저장하겠다
	};
    
    // vector<int> v2(10, -1); // 10개의 원소를 모두 -1로 초기화하겠다
    // vector<int> v3{1,2,3,4,5,6,7}; // 또다른 초기화 방법
    
    vector<Vertex> v(6); // 아래 resize 와 아주 똑같은 의미이다
    // v.resize(6); // size
    // v.reserve(6); // capacity 아직 데이터는 없지만 이사비용 최소화를 위해 영역 확보를 하겠다!
    
    v[0].edges.push_back(&v[1]); // v 벡터의 두 번째 Vertex 객체의 주소를 추가. 이렇게 하면 그래프에서 v[0]과 v[1]의 간선(edge)이 연결됨
    v[0].edges.push_back(&v[3]);
    
    v[1].edges.push_back(&v[0]);
    v[1].edges.push_back(&v[2]);
    v[1].edges.push_back(&v[3]);
    // ...
    
    // Q) 0번 -> 3번이 연결되어 있나요?
	bool connected = false;
    
    int size = v[0].edges.size();
    for(int i = 0; i < size; i++)
    {
    	Vertex* vertex = v[0].edges[i];
        if (vertex == &v[3])
        {
			connected = true;
		}
    }
}

int main()
{

}

대신 아래와 같이 그래프를 만든다.

인접 리스트, 인접 행렬

• 인접 리스트는 각 정점마다 연결된 간선의 정보를 저장하는 자료구조이다.

• 인접 행렬은 2차원 배열을 사용하여 정점 간의 연결 정보를 나타내는 자료구조이다. 정점의 개수를 V라고 할 때, VxV 크기의 배열을 사용하여 각 위치의 값이 1이면 연결되어 있음을 나타내고, 0이면 연결되어 있지 않음을 나타낸다.

• 인접 행렬을 사용하면 정점 간의 연결 상태를 배열로 표현하기 때문에 간선의 추가 및 검색이 상수 시간O(1) 에 이루어진다. 또한, 그래프의 크기가 작거나 밀집 그래프(간선의 수가 정점의 수에 비해 많은 경우)인 경우에 유리하다.

• 하지만 인접 행렬은 정점의 개수에 비례하는 공간을 사용하기 때문에 그래프의 크기가 큰 경우 메모리를 많이 차지하게 된다. 또한, 간선이 많이 없는 희소 그래프의 경우 불필요한 메모리 낭비가 발생할 수 있다. 따라서, 그래프의 크기와 구조에 따라 적절한 자료구조를 선택하는 것이 중요하다.

#include <iostream>
using namespace std;
#include <vector>
#include <queue>

// 인접 리스트: 실제로 연결 애들'만' 넣어준다. 
void CreateGraph_2()
{
	// 정점은 여기서 관리하고
	struct Vertex
    {
    	int data;
    };
    
    vector<Vertex> v(6);
    
    // 연결 여부는 여기서 관리한다
    vector<vector<int>> adjacent; // 이중 벡터
    adjacent.resize(6);
    
    //[v][v][][v][][v]
    // adjacent[0].pusg_back(1);
	// adjacent[0].pusg_back(3);    
    adjacent[0] = {1, 3};
    adjacent[1] = {0, 2, 3};
    adjacent[3] = {4};
    adjacent[5] = {4};
    
    // Q) 0번 -> 3번이 연결되어 있나요?
    bool connected = false;
    
    int size = adjacent[0].size();
    for (int i=0; i<size; i++)
	{
		int vertex = adjacent[0][i];
        if (vertex == 3)
        {
        	connected = true;
        }
	}
    
}

// 인접 행렬
void CreateGraph_3()
{
	struct Vertex
    {
    	int data;
    };
   	
    vector<Vertex> v(6);
    
    // 연결된 목록을 행렬로 관리
    // [X][O][X][O][X][X] // vector<bool>(6, false) 이것이당
    // [O][X][O][O][X][X]
    // [X][X][X][X][X][X]
    // [X][X][X][X][O][X]
    // [X][X][X][X][X][X]
    // [X][X][X][X][O][X]
    
    // 행렬을 이용한 그래프 표현
    // 메모리 소모 심하지만, 빠른 접근
    vector<vector<bool>> adjacent(6, vector<bool>(6, false));
    adjacent[0][1] = true;
    adjacent[0][3] = true;
    adjacent[1][0] = true;
    adjacent[1][2] = true;
    adjacent[1][3] = true;
    adjacent[3][4] = true;
    adjacent[5][4] = true;
    
    // Q) 0번->3번이 연결되어 있나요?
    bool connected = adjacent[0][3];
    
    // 또는 이렇게
    vector<vector<int>> adjacent2 = 
    {
    	{-1, 15, -1, 35, -1, -1},
        {15, -1, +5, 10, -1, -1},
        {-1, +5, -1, -1, -1, -1},
        {35, 10, -1, -1, +5, -1},
        {-1, -1, -1, +5, -1, +5},
        {-1, -1, -1, -1, -+5, -1}
    };
}


int main()
{
	vector<int> v;
    
}

• 여기서 재귀 함수를 쓰지 않는 이유는 그래프는 무한루프가 생길 수도 있기 때문이다
  그래서 이제 그래프 탐색 방법론이 중요한데, 가장 기본 중의 기본이 DFS, BFS 이다.