이번에는 DFS, BFS, 다익스트라, A* 알고리즘 에 대해서 살펴본다.
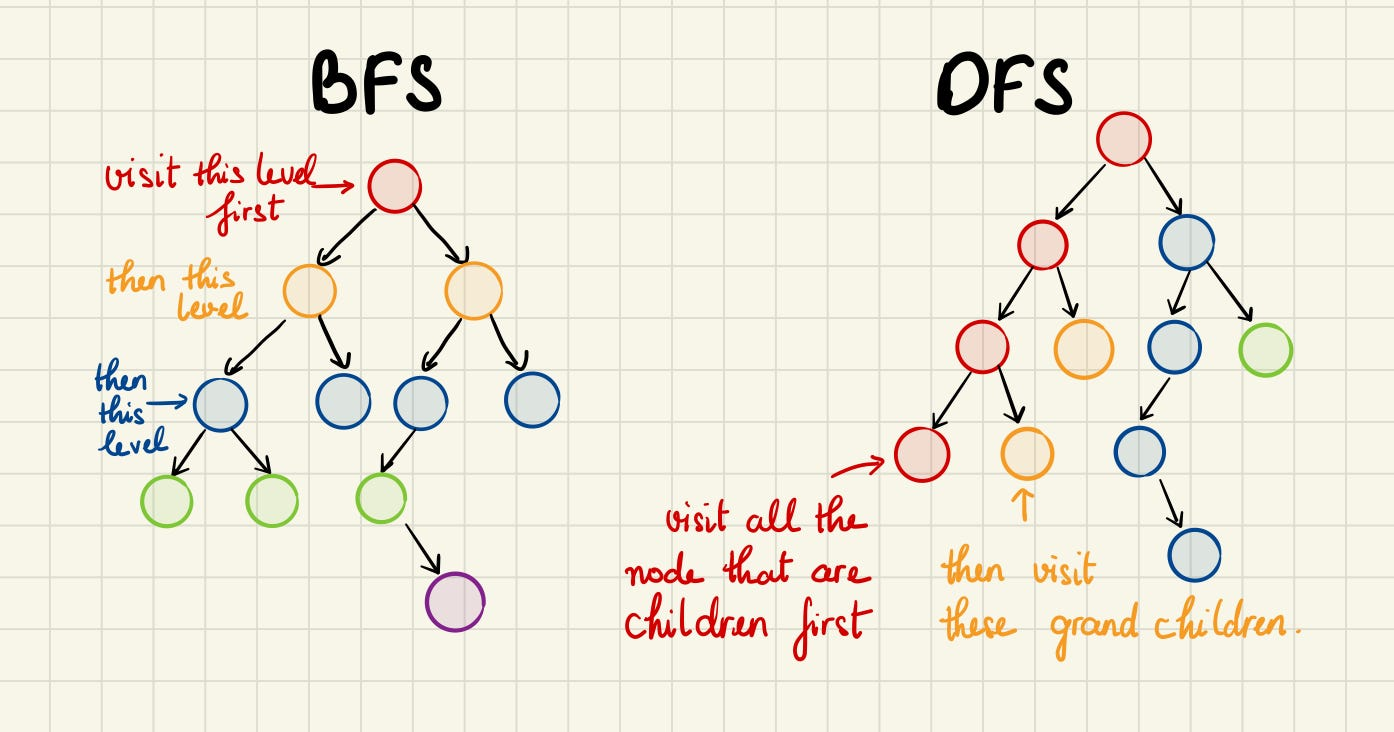
DFS와 BFS의 차이는 탐색 순서 에 있다.
DFS는 한 정점에서 시작하여 가능한 한 깊게 탐색하고, 더 이상 갈 수 없을 때 다시 이전 정점으로 돌아가서 다른 경로를 탐색한다. DFS는 재귀적인 구현이 가능하며, 그래프에서 경로를 찾거나 그래프의 구조를 분석하는 데 사용된다.
BFS는 한 정점에서 시작하여 해당 정점과 인접한 정점들을 모두 탐색한 후, 그 다음으로 인접한 정점들을 탐색한다. BFS는 최단 경로 문제나 상태 공간 탐색 등에서 활용된다.
DFS (Depth First Search)
DFS는 싸이클 여부, 끊겨있는지 여부 등등에 대해 알아볼 수 있다는 점에서 BFS 보다 할 수 있는 것이 더 많다.
DFS의 구현방법에서 인접리스트, 인접행렬 중 무엇이 더 빠를까?
정답은 없다. 데이터가 희소하지 않다면 인접행렬이 더 적합하겠다.
#include <iostream>
using namespace std;
#include <vector>
#include <queue>
struct Vertex
{
// ...
};
vector<Vertex> vertices;
vector<vector<int>> adjacent;
// 내가 방문한 목록
vector<bool> visited;
void CreateGraph()
{
vertices.resize(6);
// 인접 리스트 : 나랑 인접한 애들만 쏙쏙 들고 있겠다!
adjacent = vector<vector<int>>(6);
adjacent[0] = {1, 3};
adjacent[1] = {0, 2, 3};
adjacent[3] = {4};
adjacent[5] = {4};
// 인접 행렬
adjacent = vector<vector<int>>
{
{0, 1, 0, 1, 0, 0},
{1, 0, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0},
};
}
void Dfs(int here) // 시작점을 here 로 잡아준다
{
// 내가 어디까지 방문했는지 계속 추적해줘야 한다
// 인접리스트 버전 O(V+E)
/*
visited[here] = true;
cout << "Visited : " << here << endl;
// 인접한 길을 다 체크해서
int size = adjacent[here].size();
for (int i=0; i < size; i++)
{
int there = adjacent[here][i];
if (visited[there] == false)
Dfs(there);
}
*/
// 인접행렬 버전 O(V^2)
for (int there = 0; there < 6; there++)
{
// 길은 있는지
if (adjacent[here][there] == 0)
continue;
// 아직 방문하지 않은 곳에 한해서 방문
if (visited[there] == false)
Dfs(there);
}
}
void DfsAll()
{
visited = vector<bool>(6, false);
for (int i=0; i<6; i++)
if (visited[i] == false)
Dfs(i);
}
int main()
{
CreateGraph();
// visited = vector<bool>(6, false);
// Dfs(0);
DfsAll();
}
추가 예
#include <iostream>
#include <vector>
using namespace std;
// 기본 dfs 함수 정의
// 그래프에 포함되어 있는 노드의 개수가 8개라고 한다면
bool visited[9];
vector<int> graph[9]; // 인접리스트로 만들 때
void dfs(int x)
{
visited[x] = true; // 현재 노드를 방문 처리
cout << x << ' ';
// 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for (int i = 0; i < graph[x].size(); ++i)
{
int y = graph[x][i];
if (false == visited[y])
{
dfs(y);
}
}
}
// dfs를 응용한 문제
// N x M 배열에서 1은 칸막이, 0은 공간
// 칸막이로 나눠지는 구간의 개수는?
int n, m;
int visited[1001][1001];
bool dfs(int x, int y)
{
// 범위 체크
if (x < 0 || y < 0 || n <= x || m <= y)
{
return false;
}
if (0 == visited[x][y])
{
// 방문 처리
visited[x][y] = 1;
// 상하좌우 재귀적 호출
dfs(x - 1, y);
dfs(x, y - 1);
dfs(x + 1, y);
dfs(x, y + 1);
return true;
}
return false;
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
scanf("%1d", &graph[i][j]);
}
}
int result = 0;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
// 처음 방문하는 구역만 count 측정
if (true == dfs(i, j))
{
++result;
}
}
}
cout << result;
return 0;
}BFS (Breadth First Search)
"Breadth"는 영어로 "너비"를 의미한다. BFS에서 "Breadth"는 탐색을 너비(수평 방향)로 진행한다는 의미를 가지고 있다. 즉, BFS는 시작 정점에서부터 인접한 정점들을 먼저 탐색하는 방식으로 동작한다. 그리고 해당 단계의 탐색이 끝나면 다음 단계에서는 이전 단계에서 방문되지 않은 인접 정점들을 탐색한다. 이런식으로 너비(수평 방향)로 정점을 탐색하면서 그래프나 트리를 탐색하는 알고리즘을 BFS라 한다.
#include <iostream>
using namespace std;
#include <vector>
#include <queue>
struct Vertex
{
};
vector<Vertex> vertices;
vector<vector<int>> adjacent;
void CreateGraph()
{
vertices.resize(6);
// 인접 리스트 : 나랑 인접한 애들만 쏙쏙 들고 있겠다!
adjacent = vector<vector<int>>(6);
adjacent[0] = {1, 3};
adjacent[1] = {0, 2, 3};
adjacent[3] = {4};
adjacent[5] = {4};
// 인접 행렬
adjacent = vector<vector<int>>
{
{0, 1, 0, 1, 0, 0},
{1, 0, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0},
};
}
void Bfs(int here)
{
}
int main()
{
CreateGraph();
Bfs(0);
}
추가 예
#include <iostream>
#include <queue>
using namespace std;
// 기본 bfs 함수 정의
// 그래프에 포함되어 있는 노드의 개수가 8개라고 한다면
bool visited[9];
vector<int> graph[9];
void bfs(int start)
{
queue<int> q;
q.push(start);
visited[start] = true; // 현재 노드를 방문 처리
while (false == q.empty()) // 큐가 빌 때까지 반복
{
int x = q.front(); // 큐에서 하나의 원소를 뽑아 출력
q.pop();
cout << x << ' ';
for (int i = 0; i < graph[x].size(); ++i) // 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
{
int y = graph[x][i];
if (false == visited[y])
{
q.push(y);
visited[y] = true;
}
}
}
}
// bfs를 응용한 문제
// N x M 배열에서 1은 벽, 0은 길
// (1,1)에서 시작하여 (n,m)까지의 최소거리는?
int n, m;
int graph[201][201];
// 이동할 4가지 방향 정의 (상, 하, 좌, 우)
int dx[] = { -1, 1, 0, 0 };
int dy[] = { 0, 0, -1, 1 };
int bfs(int x, int y)
{
queue<pair<int, int>> q;
q.push(make_pair(x, y));
while (false == q.empty())
{
int x = q.front().first;
int y = q.front().second;
q.pop();
// 현재 위치에서 4가지 방향 확인
for (int i = 0; i < 4; ++i)
{
int nx = x + dx[i];
int ny = y + dy[i];
// 범위를 넘어간 경우
if (nx < 0 || ny < 0 || n <= nx || m <= ny)
{
continue;
}
// 벽인 경우
if (0 == graph[nx][ny])
{
continue;
}
// 첫 방문한 경우 최단거리 기록
if (1 == graph[nx][ny])
{
graph[nx][ny] = graph[x][y] + 1;
q.push(make_pair(nx, ny));
}
}
}
// 도착 지점 최단거리 반환
return graph[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
scanf("%1d", &graph[i][j]);
}
}
cout << bfs(0, 0);
return 0;
}
/*
// 기본 bfs에 대한 main()
int main(void) {
// 노드 1에 연결된 노드 정보 저장
graph[1].push_back(2);
graph[1].push_back(3);
graph[1].push_back(8);
// 노드 2에 연결된 노드 정보 저장
graph[2].push_back(1);
graph[2].push_back(7);
// 노드 3에 연결된 노드 정보 저장
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);
// 노드 4에 연결된 노드 정보 저장
graph[4].push_back(3);
graph[4].push_back(5);
// 노드 5에 연결된 노드 정보 저장
graph[5].push_back(3);
graph[5].push_back(4);
// 노드 6에 연결된 노드 정보 저장
graph[6].push_back(7);
// 노드 7에 연결된 노드 정보 저장
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);
// 노드 8에 연결된 노드 정보 저장
graph[8].push_back(1);
graph[8].push_back(7);
bfs(1);
}
*/다익스트라
왜 필요한가? BFS의 한계를 극복하기 위해 가중치를 더한 것이다.
더 좋은 경로를 찾아서 가는 것이 BFS 와 다익스트라의 유일한 차이이다.
예약시스템에서 먼저 등록된 것을 꺼내는 것이 BFS 이고 -> QUEUE
예약시스템에서 점수가 제일 좋을 것 같은 베스트 케이스를 꺼내는 것이 다익스트라이다. -> PRIORITY QUEUE
#include <iostream>
using namespace std;
#include <vector>
#include <queue>
struct Vertex
{
};
vector<Vertex> vertices;
vector<vector<int>> adjacent;
void CreateGraph()
{
vertices.resize(6);
adjacent = vector<vector<int>>(6, vector<int>(6, -1));
adjacent[0][1] = adjacent[1][0] = 15;
adjacent[0][3] = adjacent[3][0] = 35;
adjacent[1][2] = adjacent[2][1] = 5;
adjacent[1][3] = adjacent[3][1] = 10;
adjacent[3][4] = adjacent[4][3] = 5;
adjacent[5][4] = adjacent[4][5] = 5;
}
struct VertexCost
{
VertexCost(int cost, int vertex) : cost(cost), vertex(vertex) { }
bool operator<(const VertexCost& other) const
{
return cost < other.cost;
}
bool operator>(const VertexCost& other) const
{
return cost > other.cost;
}
int cost;
int vertex;
};
//std::pair<int, int>
void Dijikstra(int here)
{
priority_queue<VertexCost, vector<VertexCost>, greater<VertexCost>> pq;
vector<int> best(6, INT32_MAX);
vector<int>parent(6, -1);
pq.push(VertexCost(0,here)); // 0번 cost로 here점이 등장할 것
best[here] = 0;
parent[here] = here;
while(pq.empty() == false)
{
// 제일 좋은 후보를 찾는다
VertexCost v = pq.top();
pq.pop();
int cost = v.cost;
here = v.vertex;
// 더 짧은 경로를 뒤늦게 찾았다면 스킵
if (best[here] < cost)
continue;
// 방문
cout << "방문!" << here << endl;
for (int there = 0; there < 6; there++)
{
// 연결되지 않았다면 스킵
if (adjacent[here][there] == -1)
continue;
// 더 좋은 경로를 과거에 찾았으면 스킵
int nextCost = best[here] + adjacent[here][there];
if (nextCost >= best[there])
continue;
// 지금까지 찾은 경로 중에서는 최선의 수치라면 갱신
best[there] = nextCost;
parent[there] = here; // 나중에 갱신될 수 있음
pq.push(VertexCost(nextCost, there));
}
}
}
int main()
{
CreateGraph();
Dijikstra(0);
}
A* 길찾기 알고리즘
BFS, 다익스트라의 아쉬운 점? 목적지(출구)의 부재.
목적지를 아는 다익스트라가 A* 이다.
채점 (일단 이렇게 간주하겠다! 채점 방식은 케바케입니다)
- 입구에서부터 얼마나 떨어져 있는지?
- 출구에서부터 얼마나 떨어져 있는지?
- F = G + H
- F = 최종 점수 (작을 수록 좋음)
- G = 시작점에서 해당 좌표까지 이동하는데 드는 비용
- H = (휴리스틱) 목적지에서 해당 좌표까지 이동하는데 드는 비용
정리해보자!
그래프는 정점과 간선이 연결되어있는 것이고 탐색하는 방법이 여러 가지가 있는데
전체를 순회할 때 깊이를 우선적으로 할 것인지 너비를 우선적으로 할 것인지에 따라서 DFS, BFS 로 나뉘는데 BFS는 너비 우선 탐색이다. 그리고 구현을 할 때는 큐를 기반으로 구현하는 것이 일반적일 것이다. 그 이유는 발견한 순서대로 방문하는 것이므로 큐가 합리적일 것이다.
내가 발견한 순서대로 방문하다보니까 즉 너비가 우선되어 가다보니까 길찾기랑 관련이 있는 것이
가장 가까운 점부터 서칭하니, 목적지 발견했을 때 경로를 보면 그것이 최단 거리가 될 수 있다.
단점은 목적지 없이 쭉 간다는 것이다.
다익스트라도 목적지가 없는 것은 마찬가지다. 그래서 특정 방향으로 향하지 않기 때문에 여전히 뒤로 서칭하는 것이 유효하다. 다익스트라는 가중치를 둬서 나중에라도 더 좋은 길을 선택할 수 있게 해준다. 가중치가 생김으로써 물,불이 있을 다양한 상황을 추가할 수 있다.
마지막으로 A* 는 현재 내 좌표를 기준으로 목적지를 바라보고 이동하려고 시도하므로 어지간해서는 DFS, BFS 보다는 옳은 확률로 향할 수 있다. 결과는 비슷할지언정 계산한 히스토리를 보면 뒤를 가더라도 막혀서 가는 것이지 목적지를 '향해서' 간다는 장점이 있다.
