시계열 데이터의 가장 큰 특징은 관측값들간에 서로 연관성이 있다는 것이다. 시계열 데이터에서 관측값들간 연관이 있다는 것은 현재의 값이 과거의 값에 영향을 받고, 미래의 값이 현재의 값에 영향을 받는다는 의미이다.
이렇게 시간의 흐름에 따라 독립적이지 않은 시계열이 비정상성 시계열이다. 이후에 공부하지만 시계열 데이터를 분석하기 위해서 비정상성 시계열을 정상성 시계열로 변환해야 한다. 그전에 주어진 데이터가 정상성 시계열인지 확인하는 방법으로 ACF가 있다.
ACF(AutoCorrelation Function)는 자기상관함수로, 자기상관이란 서로 다른 두 시점과의 상관관계이다. 시계열 데이터의 상관관계를 도표를 통해 관측값들간 서로 연관성이 있는지 확인할 수 있다. ACF는 보통 과거 관측치와의 비교를 통해 계절성 판단을 주로 한다.
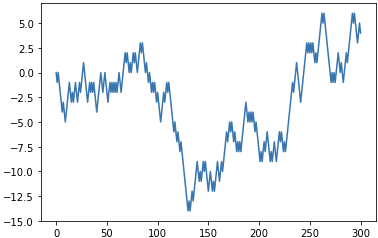
이전에 공부한 비정상성 시계열 데이터인 확률보행 코드에 ACF를 적용해보자.
# 확률보행 데이터 생성
import numpy as np
import matplotlib.pyplot as plt
probability = [0.5, 0.5]
start = 0
rand_walks = [start]
rand_point = np.random.random(300)
down_probability = rand_point < probability[0]
up_probability = rand_point >= probability[1]
for down, up in zip(down_probability, up_probability):
rand_walks.append(rand_walks[-1]-down+up)
plt.plot(rand_walks)
plt.show()<출력>
# ACF 적용
from statsmodels.graphics.tsaplots import plot_acf
from pandas import Series
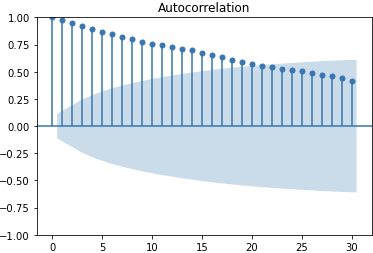
plot_acf(Series(rand_walks), lags=30, alpha=0.05)
# plot_acf(데이터의 columns, 어디 시차까지 나타낼지, alpha=0.05일때 Bartlett의 공식을 사용하여 95%의 신뢰구간으로 추정된 표준편차)
plt.show()
<출력>
x축은 lag(시점 차이)이고, y축은 두 시점의 상관관계(ACF)가 된다. lag가 2라는 것은 현시점(t)과 현 시점에서 두 시점 전(t-2)의 상관관계가 된다.
최근에 가까울수록 ACF는 1에 가깝고, 시차가 커질수록 상관관계가 떨어지므로 ACF는 0에 가까워진다. 따라서 시차가 0인경우 ACF는 1이 된다.
또 배경이 파란색인 구간은 자기상관이 0이라는 주장에 대한 95% 신뢰구간을 나타낸다. 이 구간 안에 있는 자기상관은 통계적으로 0을 의미한다. 즉, 연관성이 없다는 의미이다.
정상성 acf
정상성 시계열은 ACF를 적용했을 때 시점에 관계 없이 급격하게 변화하며 ACF가 나타나지만, 비정상성 시계열의 경우 ACF가 시점이 멀어질수록 점점 줄어든다.
정상성 데이터에 acf 적용한것도 곧 추가,,
참고 : https://velog.io/@ljs7463/%EC%8B%9C%EA%B3%84%EC%97%B4-%EB%8D%B0%EC%9D%B4%ED%84%B0-%EC%A0%95%EC%83%81%EC%84%B1%EC%95%88%EC%A0%95%EC%84%B1-stationary-AR-MR-ACF-PACF
참고 : 조신섭&황선영.(1995).시계열분석.한국방송대학교출판부
참고 : https://datalabbit.tistory.com/112
참고 : https://www.youtube.com/watch?v=abOIK40QvDA
참고 : https://www.youtube.com/watch?v=ma_L2YRWMHI&list=WL&index=1
참고: https://han-py.tistory.com/351
참고 : https://signature95.tistory.com/24