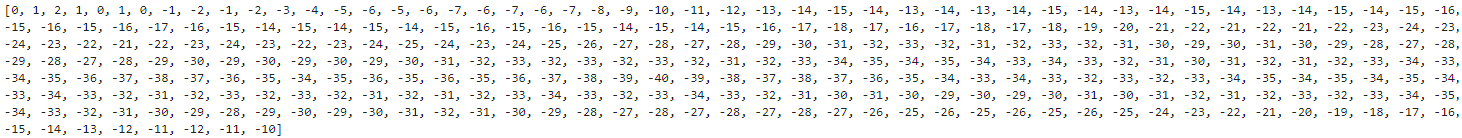시계열 데이터

---

시계열 데이터는 어떤 사건에 대한 관측치가 시간에 따라 일정 간격으로 기록되어 정렬된 데이터이다. 이러한 특징을 통해 과거의 데이터가 미래의 데이터에 영향을 주는지 확인해 볼 수 있다.

시계열 데이터는 관측값이 관측된 시점에 의존하는지에 따라 정상성(stationary) 데이터와 비정상성(non-stationary) 데이터로 나눌 수 있다.

비정상성(Non-stationary)

---

비정상성 데이터는 시간에 따라 통계적 특성이 변하는 데이터이다.
비정상 시계열은 정상 시계열에 자료의 특성인 추세성(trend) 또는 계절성(seasonality)이 내포되어 있어 데이터가 시간의 흐름에 따라 불규칙적으로 변동된다. 시계열 데이터는 현재의 상태가 과거와 미래의 상태에 밀접한 연관을 지니는 자기상관(autocorrelation)이 있는 비정상성 데이터가 많다.

비정상 시게열의 특징을 정리하면,

• 평균수준이 변하면서 추세 또는 계절성을 보인다.
• 분산이 상수가 아니면서 증가하거나 감소한다.
• 현재 관측치는 이전 관측치의 영향을 받는다.

불규칙한 자료에서 나타나는 특성을 단순화하여 불규칙하게 만드는 요인을 정리하면 다음과 같다.

• 추세성
  장기적으로 데이터에 상승이나 하강 경향성이 존재하는 것을 의미한다.

• 계절성
  일정한 빈도로 반복되는 패턴으로, 해마다 규칙적이고 주기적으로 나타나는 것을 의미한다.
  일 년 이하의 주기로 관찰했을 때 자연의 조건, 사회적 관습, 제도 등으로 인해 주기적 패턴을 갖고 계절적인 차이를 보이는 것이다.

• 주기성
  고정된 빈도가 아닌 형태로 증가나 감소의 형태를 보이는 것이다.
  계절성으로 설명되지 않는 장기적 변동이다.
  참고 : https://sodayeong.tistory.com/m/19

  예시)
  <캐나다 북서부의 맥킨지 강 지역에서 연간 포획된 스라소니의 전체 수>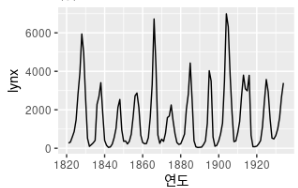

  위 그래프에서 주기가 보이기에 비정상 시계열로 생각할 수 있지만, 주기가 불규칙적이기 때문에 정상성 시계열이다. y축 값이 변하는 이유를 살펴보면, 먹이를 구하기 힘들만큼 살쾡이 개체수가 너무 많이 늘어나 번식을 멈춰서 개체수가 작은 숫자로 줄어들게 되고, 그후에 먹이를 구할 수 있게 되어 개체수가 다시 늘어나는 식이다. 장기적으로 볼 때, 이러한 주기의 시작이나 끝은 예측할 수 없기에 정상성 시계열이다.
  참고 : https://otexts.com/fppkr/stationarity.html

  y축의 주기가 예측 가능한 기간에 맞춰 규칙적으로 나타나는지, 불규칙적으로 나타나는지를 통해 주기성과 계절성을 구분하면 될 것 같다.

• 불규칙성
  사전적으로 예상할 수 없는 특수한 사건에 의해 변동되는 것이다.

비정상성 시계열 예시로는 확률보행(random walk)이 있다. 확률보행이란 임의의 방향으로 움직이는 연속적인 값으로, 시간에 따른 편차의 평균은 0이고 분산은 시간에 비례해서 증가한다. 앞/뒤로 움직일 확률이 동일해도 시간의 흐름에 따라 평균에서 점차 벗어나는 경향을 보인다. 이것이 확률보행이 비정상성인 이유가 될까.
참고 : https://codetorial.net/articles/python_random_walk.html

확률보행을 파이썬으로 구현해보자.

<확률보행 1>

import numpy as np
import matplotlib.pyplot as plt

probability = [0.5, 0.5]
# up, down일 확률

start = 0
rand_walks = [start]

rand_point = np.random.random(300)
down_probability = rand_point < probability[0]
#random 300개의 실수들이 앞으로 갈 확률(0.5)보다 작으면 True로 저장
up_probability = rand_point >= probability[1]
#random 300개의 실수들이 뒤로 갈 확률(0.5)보다 크거나 같으면 True로 저장

print(down_probability)
print(up_probability)

<출력>(생략)

for down, up in zip(down_probability, up_probability):
    rand_walks.append(rand_walks[-1]-down+up)
    #down, up이 True/False로 저장되어 있지만 
	#숫자와 연산할 땐 False->0, True->1로 취급되는것 같다. 
    
print(rand_walks)

<출력>

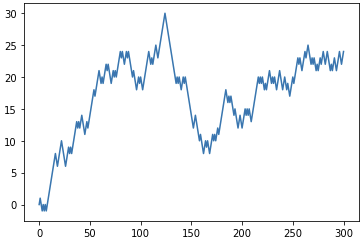
plt.plot(rand_walks)
plt.show()

<출력>

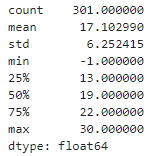
from pandas import Series

series = Series(rand_walks)
print(series.describe())

<출력>