INDEX
1. 정상성이란?
2. 정상성을 만족하는 데이터 시각화
3. 정상성 만족 여부 판별하기
4. AR? MR? ACF? PACF?
정상성(stationary)이란?
먼저 정상성에는 강한 정상성과 약한 정상성이 존재하는데 일반적으로 약한 정상성만 만족해도 된다고 보기때문에 앞으로 말하는 정상성을 약한정상성으로 보면된다.
정상성이란 시간의 흐름에 따라 평균과 분산이 일정한것(변하지않는것)을 말한다.
시계열 데이터를 예측을 하는데 있어서 데이터의 분산이 모두 제각각이고, 계절성과 추세가 있다고 가정했을때 우리는 이러한 데이터를 학습시켰을때 정확도는 매우 높게 나올 수 있다. 왜냐하면 overfitting이 되기 쉽기때문이다.
사실상 시계열데이터는 매우높은 정확도를 가지기 힘들기 때문에 너무 높은 수치가 나온다면 이러한것을 의심해 볼 수 있다.
그렇다면 어떻게해야 하는것일까??
시간의 흐름에 따라 일정한 분산과 일정한 평균을 가지고 있으면(데이터가 정상성을 가지고 있다), 평균과 분산이 안정화되어 있기때문에 분석하기 쉬울것이다.
만약에 시계열이 안정적이지 않다면 현재의 패턴이 미래에 똑같이 재현되지 않기때문에, 그대로 예측기법을 적용해서는 안된다.
따라서 정상성(안정성, stationary)는 시계열 분석에 있어서 중요하고, 나중에 소개할 ARIMA모델의 경우 이 정상성을 만족함을 가정으로 한다.
그렇다면, 자연스럽게 정상성을 만족하는 데이터와 그렇지 않은 데이터를 살펴보자
정상성을 만족하는 데이터 시각화
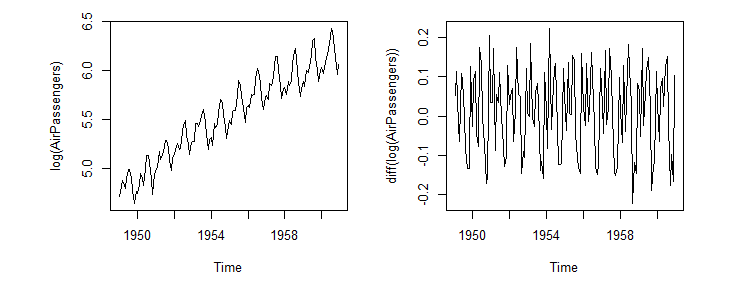
왼쪽 도표의 경우 추세가 있으며(시간이 지남에 따른 상승추세), 계절성이 있어보입니다. 즉, 정상성을 만족하지 않습니다.
반면, 오른쪽 도표의 경우 평균이0정도이며 분산 역시 위아래로 비슷한 모습입니다. 즉 오른쪽 도표가 정상성을 만족하는 데이터입니다.
그렇다면, 눈으로 확인하는 것보다 확실한 방법으로 정상성을 만족하는지 여부를 확인해 보겠습니다.
정상성 만족 여부 판별하기
1. "Dickey Fuller Test"
2. ACF 도표, PACF 도표- "(Augmented)Dickey Fuller Test"
이 방법은 통계적으로 귀무가설의 기각여부를 확인하는 방법이다.
귀무가설 : 원계열은 안정적이지 않다.(p-value > 0.05)
대립가설 : 원계열은 안정적이다.(p-value < 0.05)
( 귀무가설, 대립가설, p-value설명은 오른쪽 단어클릭 -> 귀무가설 이란? , p-value 란?)
- "ACF(Auto Correlation Function), PACF(Partial Auto Correlation Function)"
이 방법은 상관관계를 도표를 통해 확인해봄으로서 정상성 만족여부를 파악하는 방법입니다.
< 실습해보기 >
데이터불러오기
# 환율데이터 불러오기
df = pd.read_csv(****,parse_dates = ['DATE'], index_col = 'DATE')
# 일단위 데이터 -> 월단위 데이터로 변경
df = df.resample('M').last()
# 시각화
df.plot(figsize = (12, 5)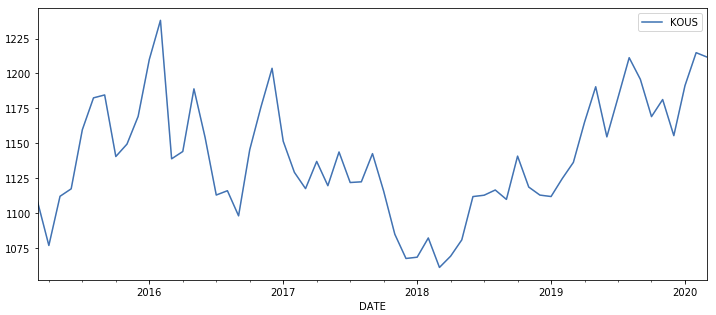
먼저 시계열 환율 데이터를 불러와서 확인해보니, 눈으로 대충 보아도 정상성이 있어 보이지 않습니다.
그렇다면 실제로 정상성 테스트를 진행해보겠습니다.
테스트 진행
- ADF Test(Augemented Dickey Fuller Test)
# stats모델의 adfuller 불러오기
from statsmodels.tsa.stattools import adfuller
# Test( KOUS : 환율 수치를 담고있는 컬럼명)
adfuller(df['KOUS'])
>>>
(-2.6235188039221238,
0.08823317575724848,
0,
1305,
{'1%': -3.4353708501743654,
'10%': -2.56795049999266,
'5%': -2.8637572934525286},
8358.34690710183)간단하게 ADF Test 를 진행하게되면 출력 결과가 나오는데 여기서 두번째 것을 확인하면 된다.
두번째 원소에는 0.08823...이 나오는데 이것이 바로 p-value가 0.088이 나온것이다.
즉, 귀무가설이 채택될 가능성이 높다는것이다. 따라서 안정성을 뛰고있지 않을가능성이 매우높다는 결론이 나온것이다.
- ACF, PACF
(ACF, PACF 설명은 아래.)
from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 시각화
# subplot생성
fig, ax = plt.subplots(1,2 , figsize = (12,4))
# acf plot
plot_acf(df, ax = ax[0])
# pacf plot
plot_pacf(df, ax= ax[1])
plt.show()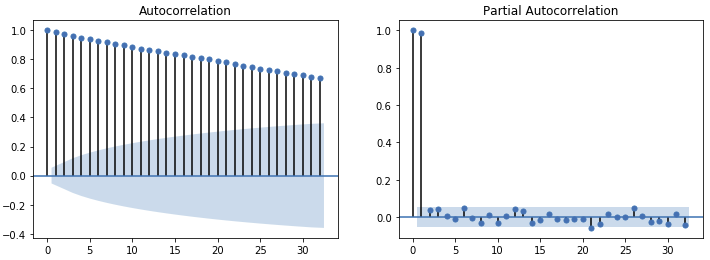
ACF 도표를 보면 매우천천히 correlation이 내려가고 신뢰구간 안에 들어가지도 못하는 모습입니다. 즉, 안정적이지 않음을 보여주고 있습니다.
또한 PACF 역시 시차 차이가 1인 것까지 correlation이 높은것 을 볼수있습니다.
이렇게 두가지 방법을 통해서 정상성 여부를 파악할 수 있습니다.
AR? MR? ACF? PACF?
지금까지의 이해와 앞으로의 내용의 이해를 위해 위 제목의 단어들을 정리해보겠습니다.
AR (Auto Regression, 자기회귀)
- AR은 시계열상의 과거 관측값을 이용하여 예측모델을 생성하는 방법이다.
- 즉, 시계열 데이터 자신의 과거 데이터를 통해서 미래를 예측하는 방법이다.
- 과거 P개의 관측값과 선형결합으로 예측하는 모델을 P차 AR모델이라고 하고 AR(P)라고 표현한다.
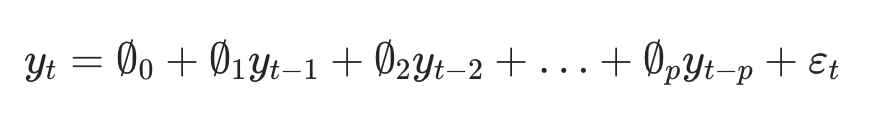
- 수식은 위와같은 모습이고 y앞에 붙은것을 자기회귀계수를 나타낸다, 맨 뒤에 있는 것은 오차 로 볼 수 있다. 그리고 t는 시차를 의미한다.
- 수식을 풀어보면 특정시차 t는 그시차의 이전시차, 그이전시차 들의 합에서 오차를 더한것과 같다.
MA (Moving Average, 이동평균)
- MA는 과거 예측 오차를 기반하여 예측하는 것이다.
- 과거 q개의 예측오차의 선형결합으로 예측하는 모델을 q차 MA모델이라 하고 MA(q)라고 표현한다.
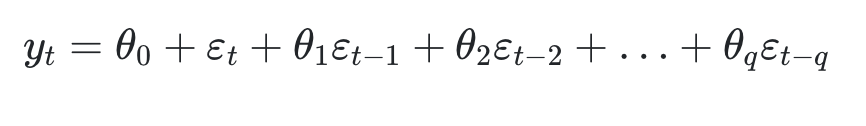
- 수식을 보면 예측오차가 더해지는것을 볼 수 있다.
ARMA(P, q)
- AR(P) 와 MA(q)를 결합 한 것으로서, 시계열의 각 값을 과거 P개의 관측값과 q개의 오차를 이용하여 예측하는 방법이다.
ARIMA(P, d, q)
- ARIMA 모형은 시계열데이터 예측에 있어서 Baseline으로도 많이 사용하고 실제로도 종종 사용하기 때문에 가장 많이알려져 있고 기본이 된다.
- ARMA모델과 다르게 중간에 I가 있는데 이것은 차분과정을 추가한 것이다.
차분이란, 현시점 데이터에서 d시점 이전에 데이터를 뺀것으로서 정상성을 만족하지 않을때 만족하게 바꾸기 위한 방법중 하나이다.
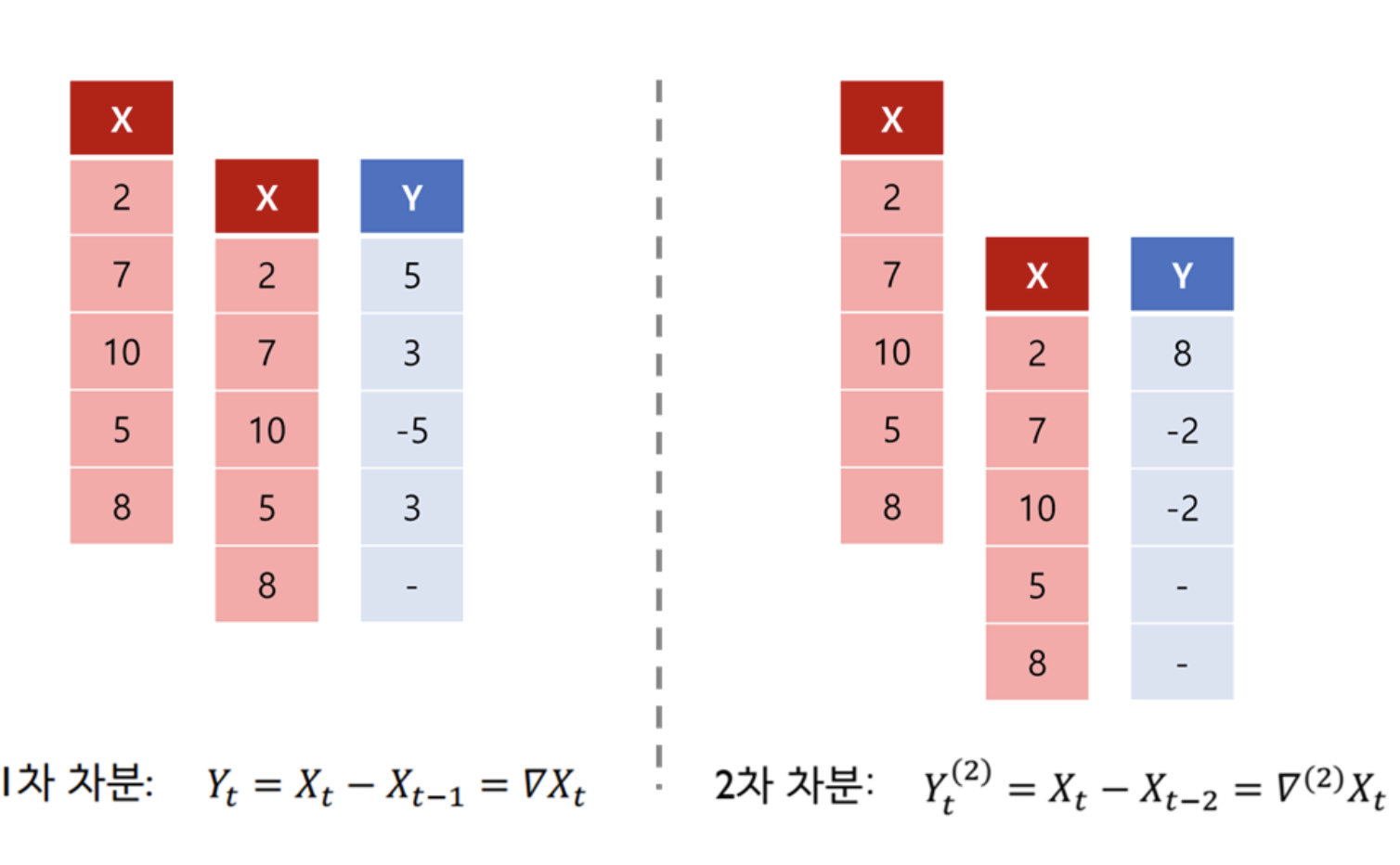이해가 잘 안된다면 정상성데이터를 만드는 방법에서 다룰때 보면 이해에 도움이 될것같다.
자료 출처: https://velog.io/@euisuk-chung/머신러닝시계열-AR-MA-ARMA-ARIMA의-모든-것-개념편
- 시계열 데이터를 d회 차분하고, 결과값은 과거 p개 관측값과 q개 오차에 의해 예측되는 모델이다.
- 결과값은 비차분화 과정을 거쳐 최종 예측값으로 변환한다. 당연하지만 차분을 통해서 정상성을 가진 데이터로 만들었으면 실제 예측시 비차분화 과정을 통해야한다. 이를테면 로그변환을 통해서 예측모델을 만들면 예측시 지수화 시켜서 예측값을 찾는것과 같은 것이라고 보면된다.
ACF, PACF
먼저 ACF, PACF를 들어가기전 자기상관(Auto Correlation)을 이해하고 가면 좋다.
자기상관(Auto Correlation)
자기 상관은 자기자신의 다른시점과의 상관관계를 말하는 것으로 시차를 적용한 상관관계를 의미한다. 즉, t시점(2000년도)의 데이터와 t-1시점(1999년도)시점의 데이터의 상관관계를 의미한다.
즉, 시차가 커지면 당연히 상관관계가 떨어질수 밖에없는데 위에서 ACF도표를 통해 정상성을 평가할때 시차가 계속 멀어져도 상관관계가 높은것으로 보여서 정상성이 없는것으로 평가할 수 있었던것이다.
ACF(Auto Correlation Function)
- 시차에 따른 일련의 자기상관을 자기상관함수(ACF)라고 한다.
- ACF는 시차에 따른 관측값 간의 연관 정도를 보여주며, 시차가 커질수록 ACF는 점차 0에 가까워진다.(시차가 멀어질수록 당연히 상관관계는 떨어지게 된다. 물론 seasonal한 데이터의 겨우 특정주기에 따라 다시 튀어오르는 구간이 있다.)
- ACF는 시계열의 정상성을 평가할 때 유용하다.
- 정상 시계열의 경우 ACF는 상대적으로 빨리 0(상관관계가 0)으로 접근한다.
- 비정상 시계열의 경우 ACF는 천천히 감소하며 종종 큰 양의 값을 가진다.
PACF(Partial Auto Correlation Function)
- 시차가 다른 두 시계열 데이터 간의 순수한 상호 연관성을 나타낸다.
- 즉, t시점과 t-1의 연관성, 그리고 t와 t-2의 연관성(이때 t-1와의 연관성은 제외한다. 순수하게 특정 시점간의 연관성(correlation)만 생각하고 사이에 있는 시점들의 연관성은 제외한다.)
- 시차에 따른 일련의 편자기 상관을 편자기 상관함수(PACF)라고 한다.
ACF도표와 PACF도표
- 시계열 데이터의 정상성 평가
- ARIMA 모델 파라미터 결정 및 모델의 적합도 평가
시계열 데이터의 정상성평가는 정상성 만족여부 판별하기에서 사용한것을 생각하면된다.
또다른 하나인 ARIMA모델의 파라미터 결정 및 모델의 적합도 평가가 있다. 이는 나중에 다룰것이다.
다음 포스팅에서는 지금까지 올린 시계열 데이터 포스팅을 기초로 정말 간단한 인사이트를 얻어보겠습니다.
