시계열 데이터
시계열 데이터는 어떤 사건에 대한 관측치가 시간에 따라 일정 간격으로 기록되어 정렬된 데이터이다. 이러한 특징을 통해 과거의 데이터가 미래의 데이터에 영향을 주는지 확인해 볼 수 있다.
시계열 데이터는 관측값이 관측된 시점에 의존하는지에 따라 정상성(stationary) 데이터와 비정상성(non-stationary) 데이터로 나눌 수 있다.
정상성(Stationary)
정상성 데이터는 해당 시계열 데이터가 관측된 시간과 무관한 데이터이다. 즉, 시간이 변해도 시계열 데이터의 통계적 특성이 일정한 특징을 가진다는 의미이다. 통계적 특성이란 주로 평균, 분산/공분산을 뜻하지만 이를 포함한 모든 분포적 특성을 총칭한다.
통계치를 구할 때는 시간의 흐름에 따른 데이터이기 때문에 구간에 대한 통계치를 확인한다.
참고 : https://velog.io/@pkb0126/%EC%8B%9C%EA%B3%84%EC%97%B4Time-Series%EC%A0%95%EC%83%81%EC%84%B1
정상성 시계열의 조건을 정리하면
- 평균수준과 진폭은 시간의 흐름에 따라 변하지 않는다
- 두 시점 사이의 공분산은 시차에만 의존한다.
공분산은 원래 두 개의 확률 변수의 선형관계를 나타내지만, 시계열({Z_1, ..., Z_n})에서는 오직 한 개의 변수(Z)만을 고려한다.
참고 : 조신섭&황선영.(1995).시계열분석_.한국방송대학교출판부
참고 : https://sodayeong.tistory.com/m/34
정상성 데이터 예시로 백색 잡음(white noise)이 있다. 백색잡음이란 평균이 0이고 분산이 일정한 상수인 정규분포를 따르며, 시간의 흐름에 따른 다른 백색잡음들과 상관관계가 0인 잡음이다. 백색 잡음은 아무런 패턴이 남아있지 않고 무작위한 진동이다.
참고 : https://direction-f.tistory.com/64
정규분포(normal distribution)는 가우스 분포(gaussian distribution)라고도 하며, 독립적이고 랜덤으로 생성된 변수를 표현한 분포이다.
참고 : https://m.blog.naver.com/with_msip/221808512417
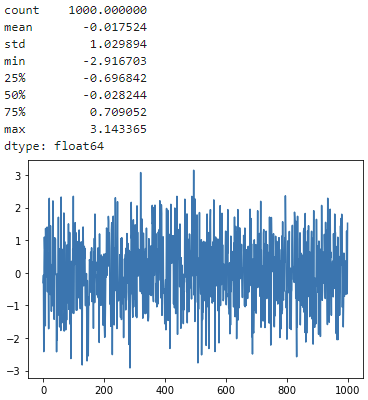
백색잡음을 파이썬으로 구현해보자. 구현 방법은 여러가지이다.
<백색잡음 1>
from random import gauss
from pandas import Series
import matplotlib.pyplot as plt
series = [gauss(0.0, 1.0) for i in range(1000)]
# random.gauss(평균, 표준편차) : 가우스 분포의 난수 반환.
series = Series(series)
# Series : 데이터프레임 하위 자료형. 1개 열->시리즈, 시리즈 모임->데이터프레임
print(series.describe())
series.plot()
plt.show()
#참고 : https://aliencoder.tistory.com/3
<출력>
계속 관찰하여도 평균이 노란선에 가깝게 위치하여 일정하고, y값이 한쪽으로 더 치우치는 모양이 되지 않는다.
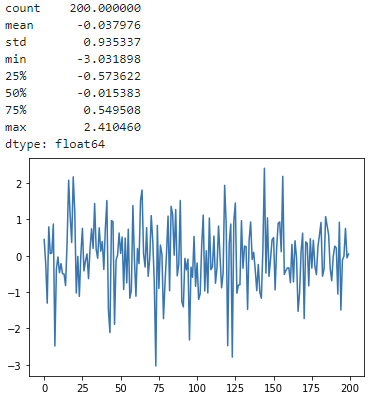
<백색잡음 2>
import numpy as np
from pandas import Series
import matplotlib.pyplot as plt
x1 = np.random.normal(0, 1, 200)
# random.normal(평균, 표준편차, 생성데이터개수)
x1 = Series(x1)
print(x1.describe())
x1.plot()
plt.show()
#참고 : https://rfriend.tistory.com/691<출력>
평균이 0, 분산이 1인 정규분포로부터 200개의 백색잡음 샘플을 추출한다.