DL Basics

2. CNN

Introduction

1) Convolution

• Convolution이라는 개념은 CNN에서 처음 나온 개념은 아니고,
  Signal processing에서 두 개의 함수가 있을 때 두 개의 함수(신호)를 잘 섞어주는 방법으로서 정의가 된다.
  
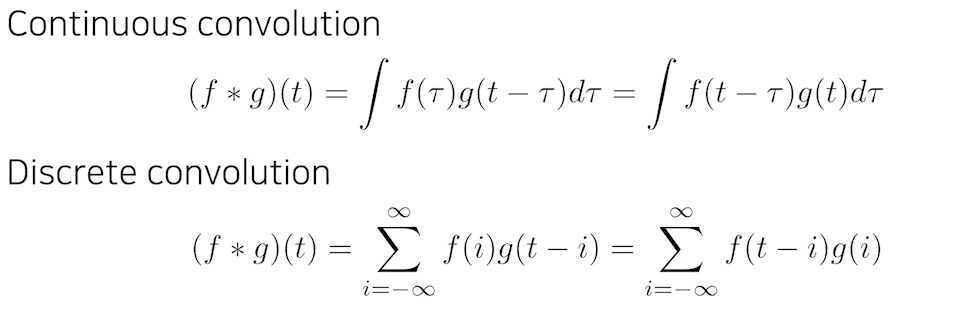
• 우리가 실제로 많이 알고 있는 2D image Convolution은 아래와 같은 수식으로 표현될 수 있다.
• I가 전체 이미지 공간을 의미하고, K가 우리가 사용하고자 하는 필터를 의미한다.
  
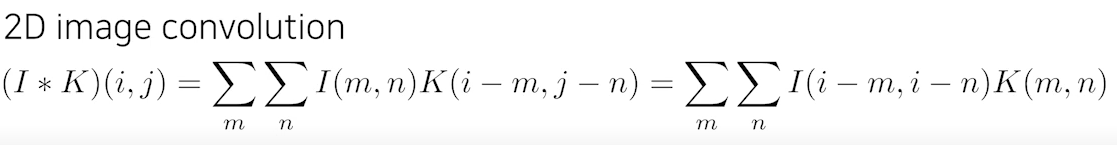
• 이제 CNN에서 convolution이 어떻게 이루어지는지를 보자.
• stride나 padding을 고려하지 않은 convolution과정을 보면,
  다음과 같이 3 x 3 필터를 7x7 이미지에 convolution을 하면 5 x 5 output이 나오게 된다.
  
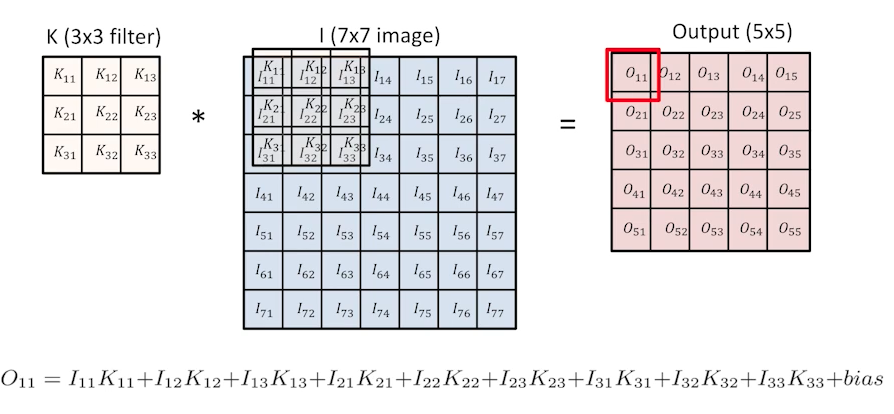
• 이 때 output의 한 칸의 값은 filter와 image의 각 위치별 값을 곱한 것의 합으로 구해지게 되고, filter가 옆으로 한 칸씩 이동하면서 값이 채워진다.
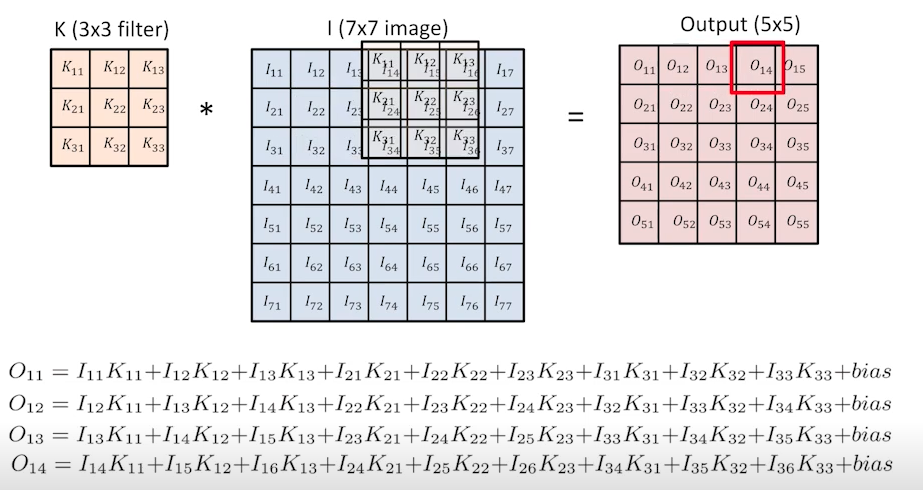
• 우리가 적용하고자 하는 필터에 따라서 같은 이미지 데이터를 집어 넣더라도 다른 결과가 나오게 된다.
• 예를 들어 3 x 3 필터의 값을 모두 1/9로 하면 output 한 칸의 값은 input 이미지의 3x3 영역 값의 평균값이 되기 때문에 blur된 이미지가 결과로 나온다.
  

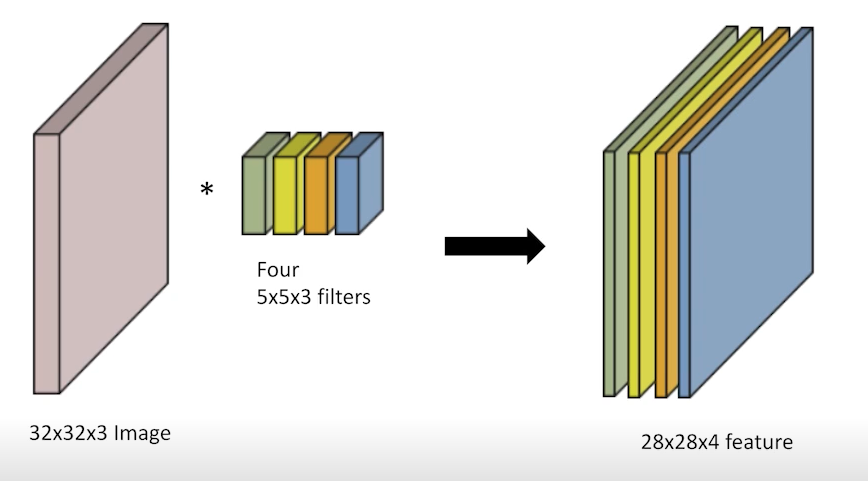
2) RGB Image Convolution

• Output, 즉 feature map의 채널을 늘리려면 어떻게 해야 할까? filter의 개수를 늘리면 된다.

3) Convolutional Arthmetic

• 당연히 CNN도 레이어를 여러개 쌓을 수 있다.

• 또한 레이어를 쌓을 때, MLP에서 배운 것과 동일하게 한 번 convolution을 거치고 나면 non linear activation을 통과하도록 설계한다.
  

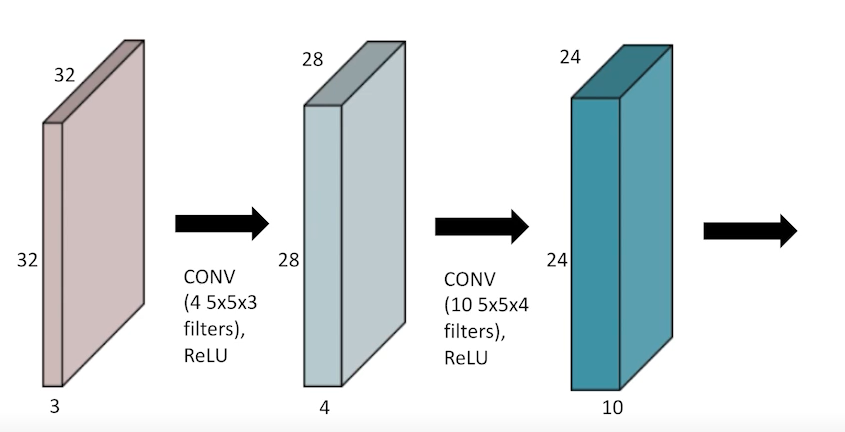
• CNN의 장점은 레이어를 여러 개 쌓더라도 Fully Connected Layer에 비해 파라미터 수를 엄청나게 적게 사용할 수 있다는 것이다.

• 파라미터 수가 너무 많으면 학습이 어렵고 generalization performance가 떨어진다.
  반대로 같거나 더 깊은 네트워크에 대해 파라미터 수가 적을수록 학습이 용이하고 generalization performance가 높다.

• 따라서 제안된 모델에서는 파라미터의 개수를 파악하는 것이 중요하다.

• CNN 파라미터 개수 계산하기

  • CNN에서, filter의 한 개의 shape은 다음과 같다.
    kernel size x kernel size x (num of input channels(입력채널 수))
  • 또한 filter의 개수는 num of output channels(출력 채널 수)와 같다.
  • 위의 두 개, 즉 filter의 shape과 개수가 파라미터 수를 결정한다.
  • 이미지의 크기와 같은 spacial dimension은 파라미터 수에 영향을 주지 않는다.
  • 해당 경우에 파라미터의 개수는 몇 개일까?
    
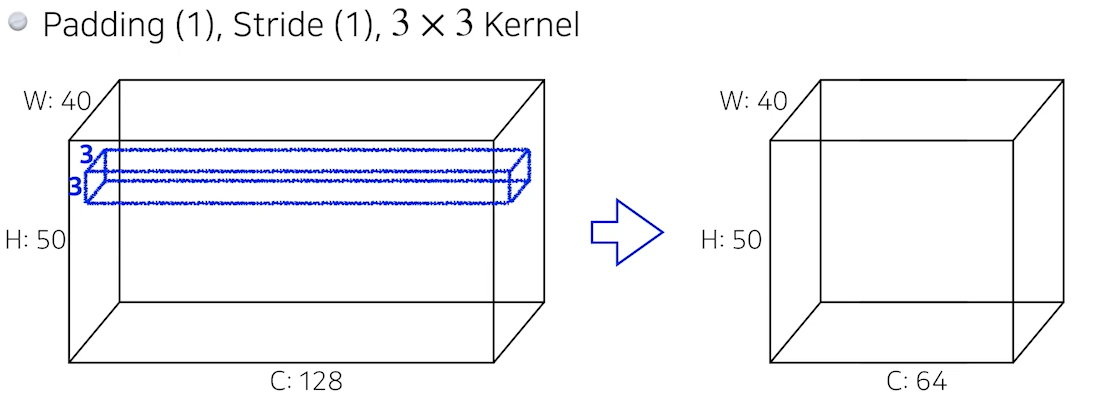
    필터(filter, kernel)의 shape은 3x3x128이고,
    출력 채널 수가 64이므로 필터는 64개가 있다.
    따라서 한 필터 당 파라미터의 개수는 3x3x128 = 1152이고,
    이러한 필터가 64개 있으므로
    총 파라미터의 개수는 1152 x 64 =73728이다.
  
  
  • Alexnet에서 파라미터 개수는 몇 개일까?
    
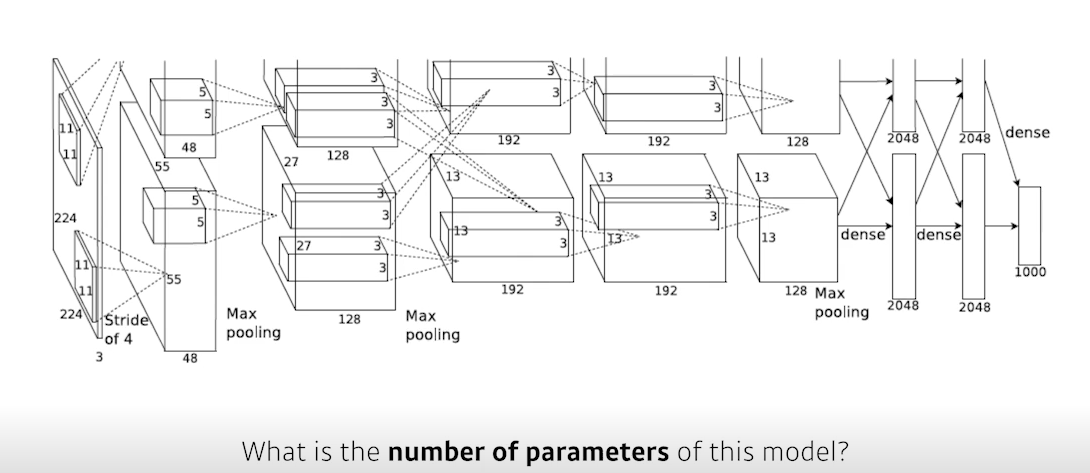
    • 참고로 AlexNet의 경우 GPU를 사용하기 위해 모델을 2개로 쪼개서 각각 다른 GPU에서 학습을 시켰기 때문에 모델이 2개로 쪼개져 있다. 그림 그대로 두 덩어리의 부분 모델로 보고 그대로 파라미터 수를 계산해주면 된다.
    • 첫번째 레이어 : 모양이 11 x 11 x 3인 필터가 출력 채널 수(=다음 feature map의 채널 수)인 48개만큼 있고, 이게 두 덩어리가 있기 때문에 총 파라미터 수는
      (11 x 11 x 3) x 48 x 2이다.
    • 두번째 레이어: 모양이 5 x 5 x 48인 필터가 출력 채널 수인 128개만큼 있고, 이게 두 덩어리가 있기 때문에 총 파라미터 수는
      (5 x 5 x 48) x 128 x 2
    • 세번째 레이어: 모양이 3 x 3 x 128인 필터가 출력 채널 수인 192개만큼 있고, 이번에는 교차를 하기 위해 4 덩어리가 있기 때문에 총 파라미터 수는
      (3 x 3 x 128) x 192 x 4
    • 네번째 레이어: 모양이 3 x 3 x 192인 필터가 출력 채널 수인 192개만큼 있고, 이게 두 덩어리가 있기 때문에 총 파라미터 수는
      (3 x 3 x 192) x 192 x 2
    • 다섯번째 레이어: 같은 원리로 직접 해보자.
      참고로 다섯번째 레이어의 총 파라미터 개수는
      (3 x 3 x 192) x 128 x 2이다.
    • 여섯번째 레이어: 여기부터는 convolution layer가 아닌 dense layer이다. dense layer의 파라미터 개수는 (입력 차원) x (출력 차원)이다. 바로 앞의 feature map을 flatten해준 뒤 2048차원으로 변환할 때 총 파라미터 개수는 (4번 mapping = 화살표 개수)
      (입력) x (출력) x (화살표 개수) = (13 x 13 x 128) x (2048) x (4)
    • 일곱번째 레이어: 총 파라미터 수 2048 x 2048 x 4
    • 여덟번째 레이어: 총 파라미터 수 2048 x 1000 x 2

4) Stride & Padding

• Stride
  • 걸음 수를 의미한다.
  • stride=1이면 filter가 한 칸씩 이동하고, stride=2이면 filter가 2칸씩 이동한다.
• Padding
  • CNN layer를 거치더라도 이미지 크기(spacial demension)가 유지될 수 있게 양 옆에 테두리를 추가하는 방법이다.
• 3x3 filter를 사용한다고 했을 때, 아래 그림에서 padding과 stride를 각각 어떻게 사용했을지 생각해보자.
  
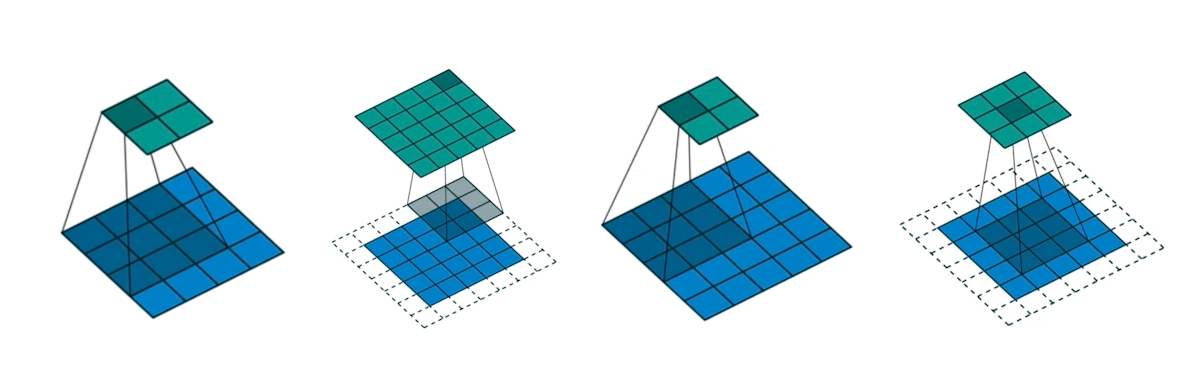
  • 첫 번째는 padding은 없고, stride=1
  • 두 번째는 padding=1, stride=1
  • 세 번째는 padding은 없고, stride=2
  • 네 번째는 padding=1, stride=2

5) Modern CNN

• 집중해야 할 부분

  • 어떻게 네트워크를 더 깊게 쌓으면서도 파라미터를 줄였는지?

• ILSVRC(ImageNet Large-Scale Visual Recognition Challenge)

  • 이미지 인식 대회
  • classification / detection / localization / segmentation 등의 task가 있다.
  • 다음과 같은 특징이 있다.
    • 1,000 different categories
    • Over 1 million images
    • Traning set : 456,567 images
      
      

• AlexNet

  • ILSVRC에서 처음으로 딥러닝을 이용하여 우승을 한 모델

  • Key ideas(사실 지금은 당연하게 사용하고 있는 요소들이 많다)

    • ReLU activation
    • GPU implementation
    • Local response normalization, Overlapping pooling
    • Data Augmentation
    • Dropout

  • AlexNet은 바로 위에서 파라미터를 계산하기 위해 우리가 구조를 미리 봤다.

    
    

• VGGNet

  • Dropout(p=0.5)
  • VGG16, VGG19
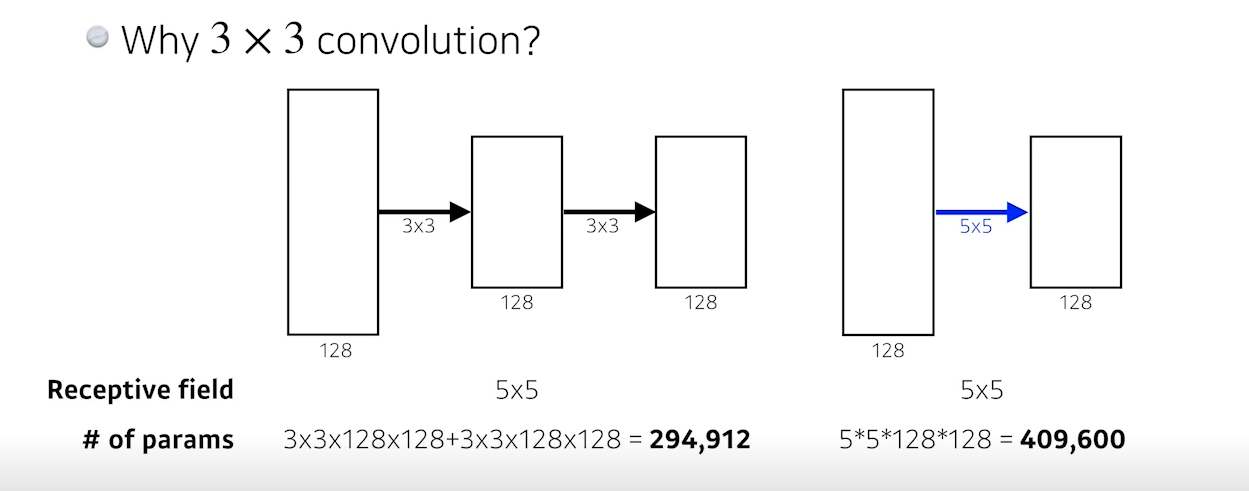
  • 5 x 5 대신에 3 x 3 Convolution을 사용(stride=1)해서 네트워크를 깊게 하면서 파라미터 수를 줄였다 -> 왜 3 x 3이 5 x 5보다 좋은가?
    • * receptive field : 하나의 feature map을 얻기 위해서 고려할 수 있는 입력의 spacial dimension
    • 3 x 3 을 2번 사용하는 것과 5 x 5를 1번 사용하는 것이 receptive field가 동일하다.(나오는 결과,즉 feature map의 크기(=spacial dimension)가 동일하다.)
    • 같은 결과를 내보내는데 3 x 3 을 2번 사용하는 것이 5 x 5 를 1번 사용하는 것보다 파라미터 수가 훨씬 적다.
      

• GoogleNet
  • Inception Block
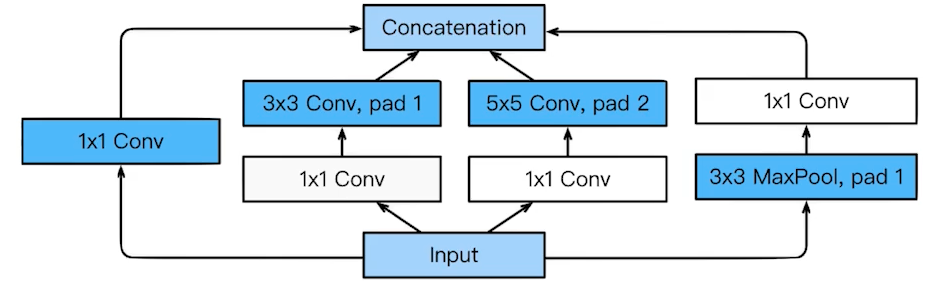
    • 하나의 입력이 들어왔을 때, 여러개로 퍼졌다가 다시 하나로 합쳐지게 된다.
      
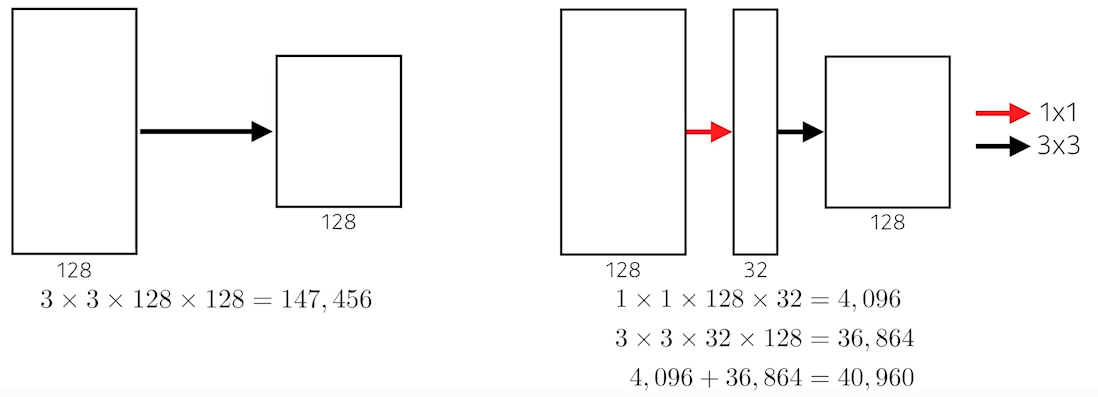
  • 1 x 1 Convolution을 도입하여 파라미터 수를 더 줄임
    • 1 x 1 convolution can be seen as channel-wise dimension reduction.
    • 파라미터 수를 계산하면, 그냥 바로 3 x 3 convolution을 한 것보다 1 x 1을 하고 나서 3 x 3을 한 경우가 파라미터 수가 더 적다.
  • 실제로 AlexNet과 VGGNet, GoogleNet의 레이어와 파라미터 수를 비교하면 다음과 같다.
    (GoogleNet이 AlexNet보다 훨씬 깊지만 파라미터 수가 훨씬 적다.)
    • AlexNet(8-layers) : 60M parameters
    • VGGNet(19-layers) : 110M parameters
    • GoogleNet(22-layers) : 4M parameters
      
      
• ResNet
  • 네트워크가 깊어질수록 Generalization performance가 떨어지는 문제를 해결하고자 제안된 방법
  • Overfitting은 아니지만 깊은 네트워크의 test error가 얕은 네크워크의 test error보다 오히려 더 크다는 문제가 있었고, 이를 해결하고자 하였다.
    
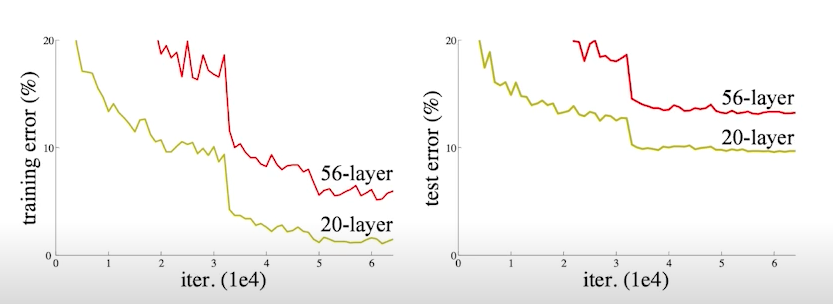
  • 네트워크에 Identity map을 추가해줌
  • skip connection을 이용하여 입력과 출력의 차이를 학습
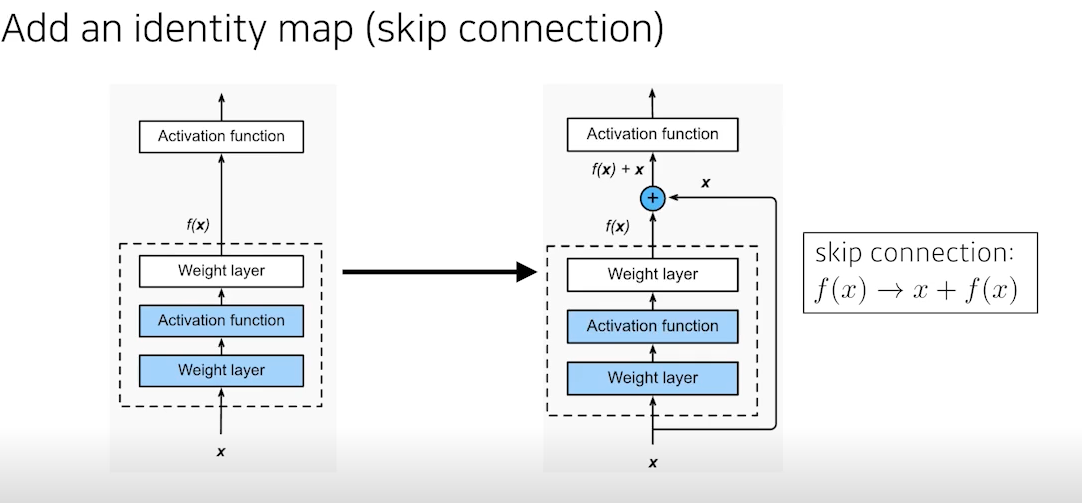
  • resnet에서도 GoogleNet의 Inception Block처럼
    파라미터를 줄이기 위해 bottleneck architecture에서 1x1 conv를 사용하여 입력 채널을 줄였다가 나중에 다시 늘려줌
    
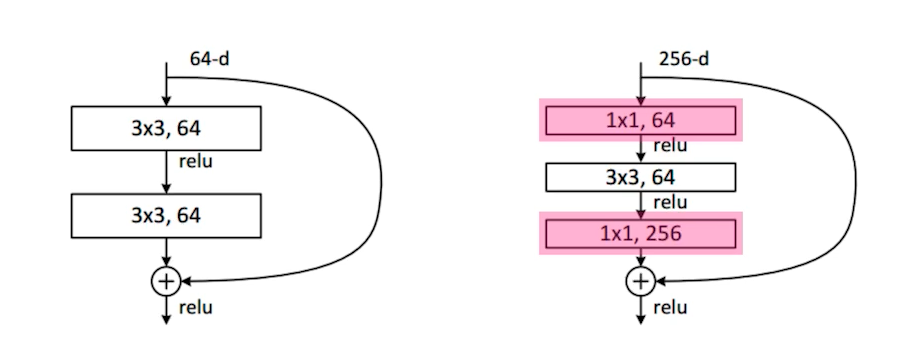
  • 네트워크를 더 깊게 쌓을 수 있게 해 줌
    
    
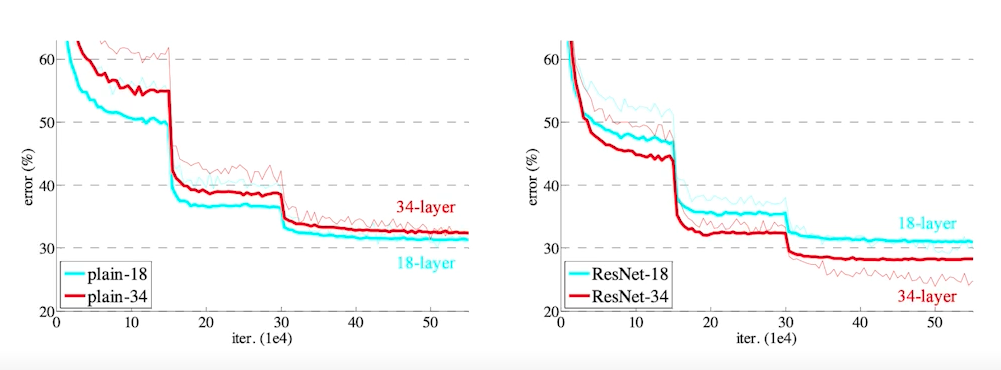
• DenseNet
  • resnet은 입력을 그대로 더하는 반면, densenet에서는 concatenate을 해줌
  • 문제는 concatenate을 하게 되면 채널이 점점 커지고, 이에 따라 파라미터 수도 같이 커지기 때문에, 중간에 한 번씩 채널을 줄여 주어야 한다.
  • 그래서 Dense Block 뒤에 Transition Block을 붙여주었다.
    • Transition Block : BatchNorm -> 1x1 Conv -> 2x2 AvgPooling
    • Transition Block을 통해 중간에 한번씩 채널을 줄일 수 있다.(dimension reduction)
  • 많은 task에서 DenseNet이 state of the art가 되는 경우가 많다.

6) CV Applications

Semantic Segmentation

• 픽셀단위로 물체, 사람을 구분하는 task
• FCN(Fully Convolutional Network)
  • 마지막에 dense layer가 있는 일반적인 CNN 네트워크와 다르게, 모든 레이어가 convolution layer로 되어 있는 구조를 가진다. 즉, dense layer를 없앴다.
    
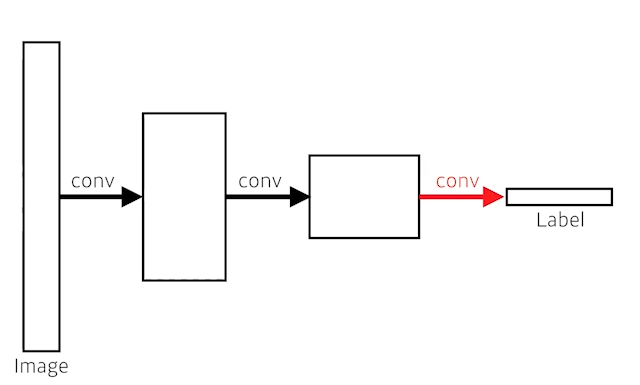
  • 사실 dense를 conv로 대체해도 전체 파라미터 수는 변하지 않는다.
    
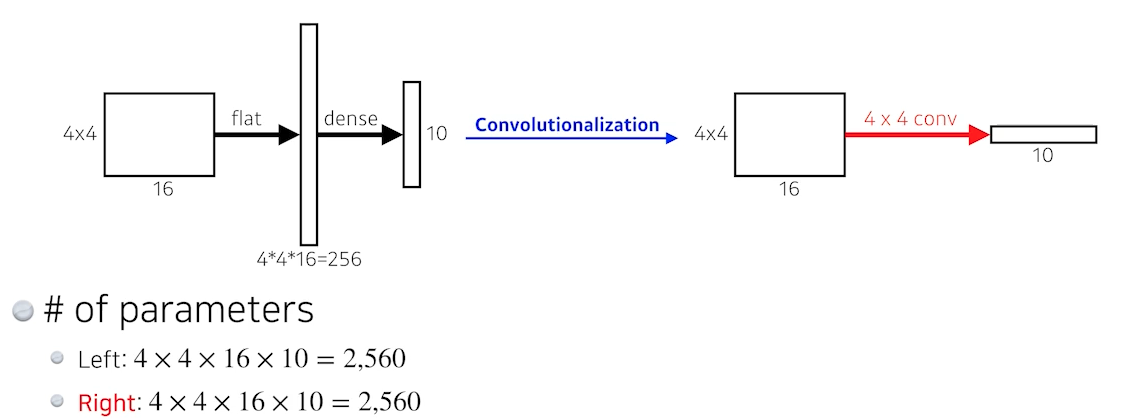
  • 그럼 왜 사용하는가?
    • dense layer와 달리 입력 이미지의 크기에 상관없이 작동할 수 있고, 출력으로 heatmap과 같은 형태가 출력된다.
    • 따라서 이를 복원하면 semantic segmentation task도 가능할 것이다.
    • 이 때, 출력을 원래의 dense picture로 바꿔줘야 한다.
    • 이렇게 차원을 다시 늘리는 방법들이 이후에 나오게 된다.
      ( 바로 다음에 소개한다)

• Deconvolution (conv transpose)
  • 직관적으로 말하면 convolution의 역연산
  • spacial dimension을 키워줌
  • 엄밀하게 들어가면 convolution은 역으로 계산할 수 없다.즉 convolution 계산한 결과를 다시 역으로 복원할 수는 없다.
    • 2 + 8 은 10이다.
    • 3 + 7 도 10이다.
    • 하지만 10만 가지고 2+8이나 3+7로 다시 복원할 수는 없다.
  • 하지만 convolution의 역이라고 생각하면 파라미터 개수나 네트워크 크기를 계산할 때 편하다.
• Results
  
  

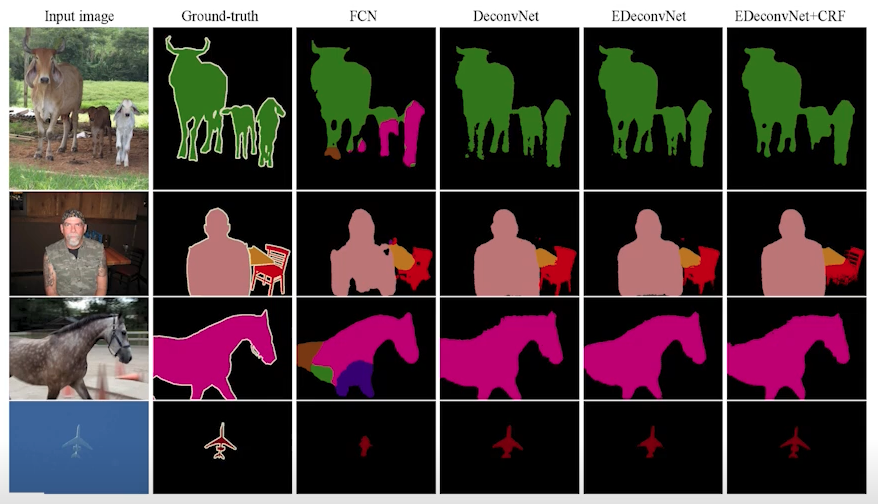
Detection

• bounding box를 통해 이미지 내에서 객체를 구별하는 task
• R-CNN
  • 1) 이미지를 입력 받는다.
  • 2) 이미지 안에서 영역의 후보들을 엄청 뽑는다.(2000개 정도)
  • 3) 영역의 후보들(bounding boxes)의 크기가 다 다르니까 크기를 똑같이 맞춘다.
  • 4) 그 다음 분류를 한다.(linear SVM으로)
  • 매우 brute force적인 방식이고, 시간이 오래 걸린다.
  • 하나의 이미지를 학습하기 위해 2000개의 이미지를 모두 CNN에 다 통과 시켜야 한다. 즉 CNN을 2000번 돌려야 한다.
  • 한 이미지 당 학습하는데 1분 정도 걸린다.
    
    
    
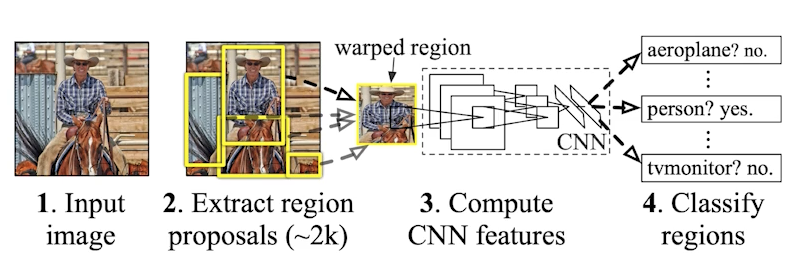
• SPPNet
  • R-CNN과 아이디어는 똑같은데, CNN을 한 번만 돌린다.
  • 먼저 이미지 안에서 bounding box를 뽑고,
  • 이미지 전체에 대해 CNN을 한 번 돌려서 convolution feature map을 만든 다음에,
  • 뽑힌 bounding box 위치에 해당하는 convolution feature map의 일부 텐서만 가져오자

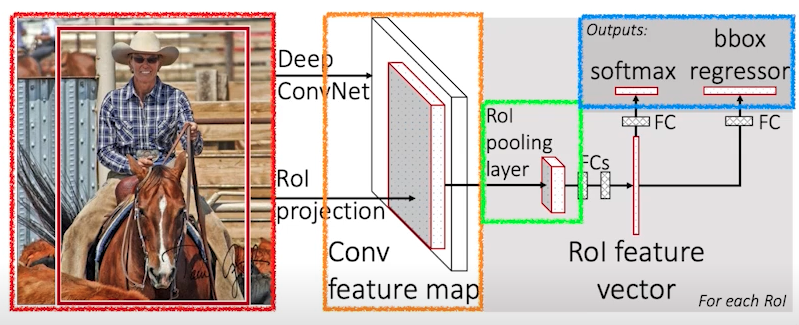
• Fast R-CNN

  • 입력 이미지를 가져오고
  • bounding box를 2000개 정도 뽑는다.
  • 그 뒤 convolution feature map을 한 번 얻는다.(SPPNet과 동일)
  • 그 다음 각각의 영역에 대해서 고정된 길이의 feature를 뽑는다.(ROI Pooling) (SPPNet과 거의 동일)
  • 마지막으로 뉴럴 네트워크를 통해서 내가 얻어낸 bounding box를 어떻게 움직이면 좋을지(bounding box regression)와 bounding box에 대한 label을 찾게 됨

• Faster R-CNN

  • Bounding box를 뽑아내는 region proposal 과정도 학습을 하자
  • Region Proposal Network + Fast R-CNN
    
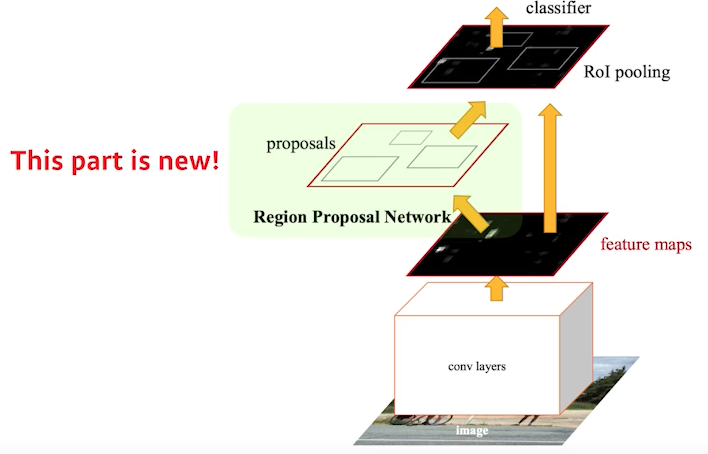
  • Region Proposal Network
    • 이미지에서 특정 영역이 bounding box로서의 의미가 있을지 없을지, 여기 안에 물체가 있을 것 같은지 아닌지 판단
    • anchor boxes : 미리 정해놓은 bounding box의 크기
      
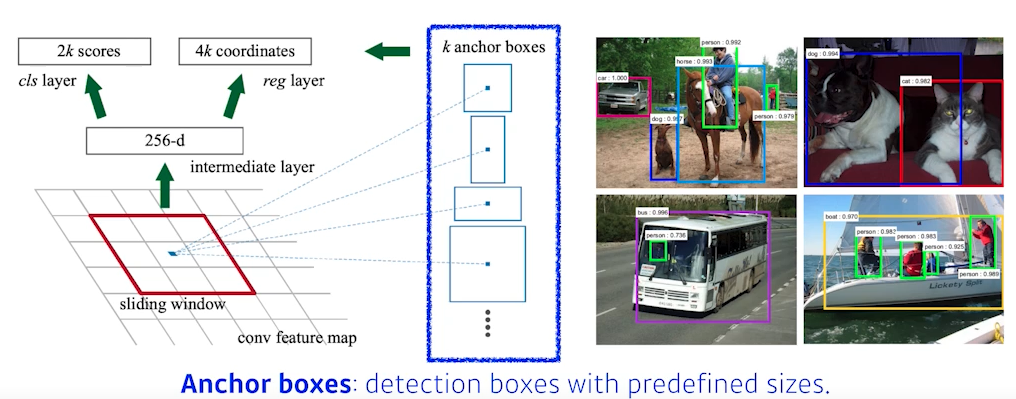
    • 파라미터
      • 9 : 3개의 region size(128, 256, 512)와 3개의 비율 (1:1, 1:2, 2:1)
      • 4: 하나의 네모 박스의 width, height, offset x, offset y
      • 2: 해당 bounding box가 쓸모가 있는지 없는지
      • 총 9 x (4 + 2) = 54
        
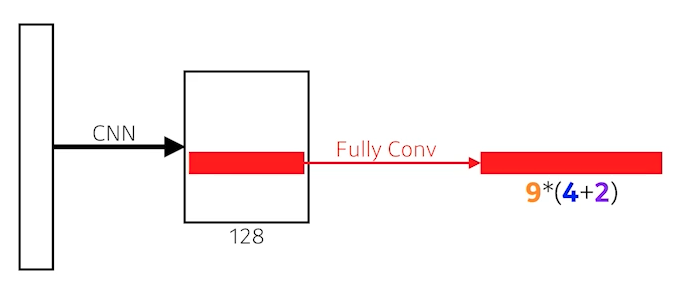
  • 이전 모델들에 비해 결과가 잘 나오는 것을 볼 수 있다.
    
  
  

YOLO

• extremely fast object detection algorithm
• baseline : 45fps, smaller version : 155fps
• 여러 개의 bounding box도 예측하는 동시에, 분류도 진행하기 때문에 빠름
  
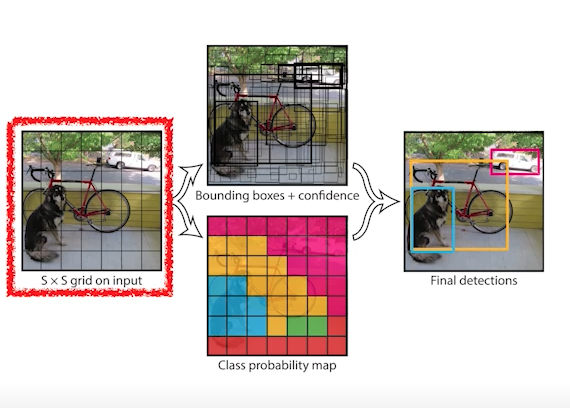
• 1) 이미지가 들어오면 이미지를 S x S grid로 나누게 된다.
• 2) 내가 찾고 싶은 물체 중앙이 해당 그리드 안에 들어가면 그 그리드 셀이 해당 물체에 대한 bounding box와, 그 해당 물체가 무엇인지를 동시에 예측해줌.
  • 각각의 셀은 B(ex.5)개의 bounding box를 예측하게 되고, 그 box가 쓸모있는지도 같이 예측한다.(가운데 위의 그림)
  • 그 와 동시에, 이 그리드 셀에 속하는 물체가 어떤 클래스에 속하는지 예측한다.(가운데 아래 그림)
  • 두 개의 정보 취합
• 최종적으로,
  • S x S : grid 에 있는 셀의 개수
  • B x 5 : 한 box 당 (x, y, w, h) 그리고 쓸모있는지 없는지에 대한 confidence까지 총 5개 & 이러한 box가 B개 있음
  • C : Number of classes
  • 종합적으로 크기 S x S , 채널 (B x 5 + C) 의 텐서를 만들면 YOLO가 된다.
• YOLO 결과
  

회고 및 질문

이전에는 원리까지 이해하지 못하고 가져다만 썼던 YOLO에 대해 제대로 알게 되었다. 이번 기회에 논문도 제대로 읽어봐야 겠다.
참고: yolo 정리
https://bkshin.tistory.com/entry/%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0-YOLOYou-Only-Look-Once

1. 왜 kernel의 size는 항상 홀수일까?
   https://datascience.stackexchange.com/questions/23183/why-convolutions-always-use-odd-numbers-as-filter-size