DL Basics

1-2. Multi-Layer Perceptron

Neural Networks

1) Neural Networks의 의미

Neural networks are computing systems vaguely inspired by the biological neural networks that constitute animal brains.

• 위 문장은 우리가 많이 들어본 AI 에 대한 정의와 비슷하게, 뉴럴 네트워크가 동물의 뇌를 모방한 컴퓨터 시스템이라고 표현한다.
• 하지만 이렇게만 표현하기에는 딥러닝은 뇌를 모방하는 분야 외의 분야로 이미 많이 갈라졌다.
• 또한 동물의 뇌를 모방한다고 해서, 꼭 메커니즘까지 같아야 하는 것은 아니다. 따라서 뉴럴 네트워크 또한 동물의 뇌와 비슷한 기능을 하는 것을 목표로 하는 것이지, 뇌의 메커니즘을 모방했다고 하기에는 비약이 있다.
• 좀 더 담백하고 오해가 없을만한 표현은 다음과 같다.

Neural networks are function approximator that stack affine transformations followed by nonlinear transformations.

• 즉, 선형 변환과 비선형 변환을 쌓아서 만든 function approximators(어떤 함수에 근사하는 것)를 Neural Networks라 한다.

2) Linear Neural Networks

• 가장 간단한 선형 변환부터 보자
• 학습의 과정은 다음과 같다.
  • 먼저 Data가 있을 때, 선형 모델을 설정하고 Loss를 정한다.
    
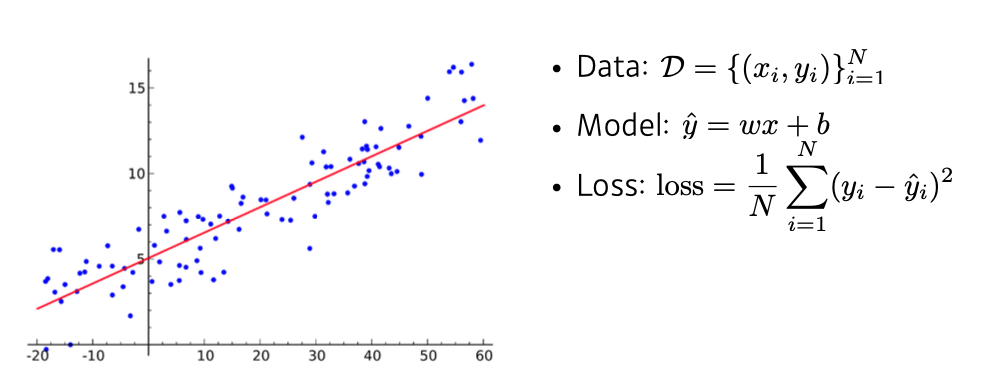
  • 그 뒤 loss를 파라미터에 대해 편미분한다.
    
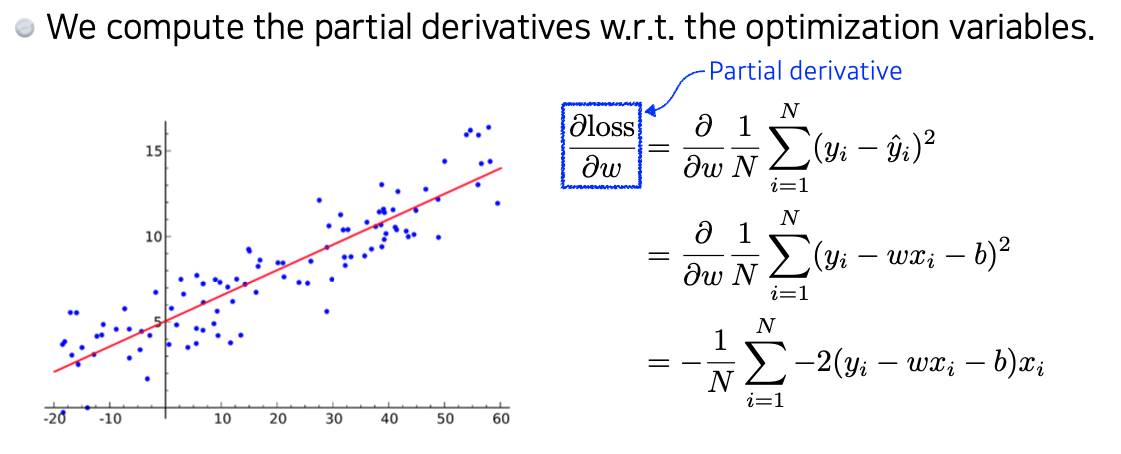
  • 여기에서는 파라미터가 W, b 두 개이므로 두 개에 대해 각각 편미분한다.
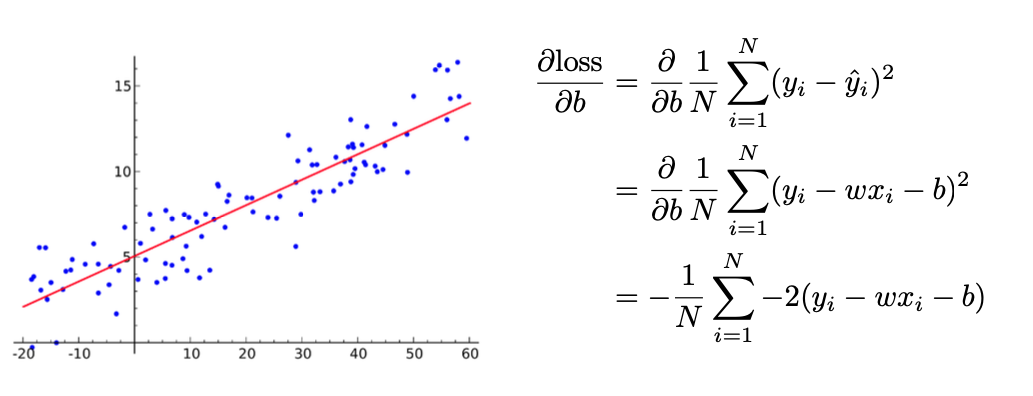
  • 이렇게 미분한 값을 이용하여 파라미터를 업데이트 한다.
• 당연히 여러 차원을 가진 input, output에 대해서도 행렬 연산을 통해 동일하게 학습을 진행할 수 있다.
  
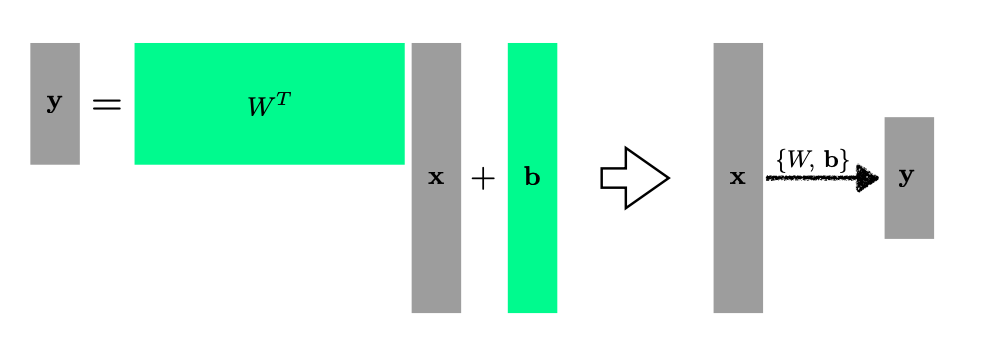
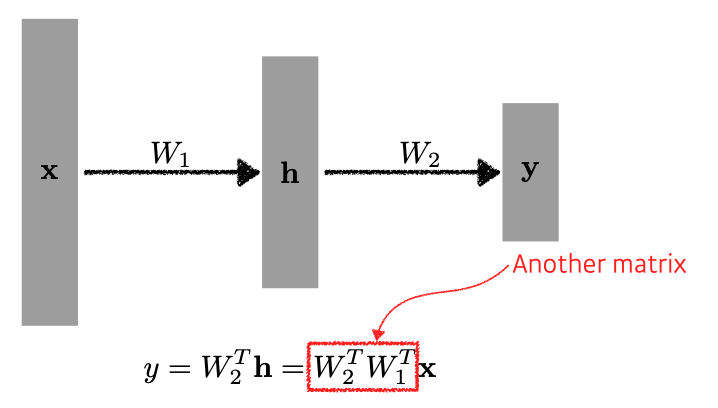
• 만약에 여기에서 layer를 더 쌓고 싶다면? 또 다른 weight matrix를 가져와서 한 번 더 선형 변환을 해주면 된다.

Multi Layer Perceptron

1) Multi-Layer Perceptron

• Linear layer의 한계점은 표현력이 늘지 않는다는 것이다. 선형 변환에 다시 선형 변환을 하면 그대로 선형만 되기 때문이다.

• 이해하기 쉽게 설명을 하자면, 합성함수를 만들려고 하는데,
  두 직선 함수 f(x) = 2x, g(x)=3x에 대해 합성함수 g(f(x))는 3(2x) = 6x이므로 직선이다.
  f(g(x))도 동일하게 직선이고, f(x)와 g(x)를 아무리 합성해도 결국 표현할 수 있는 것은 직선밖에 없다.

• 같은 이유로, 선형 layer만 계속 쌓는다면 표현력이 좋아지기 않기 때문에 비선형 함수를 사이에 넣어서 표현력을 높일 수 있다.

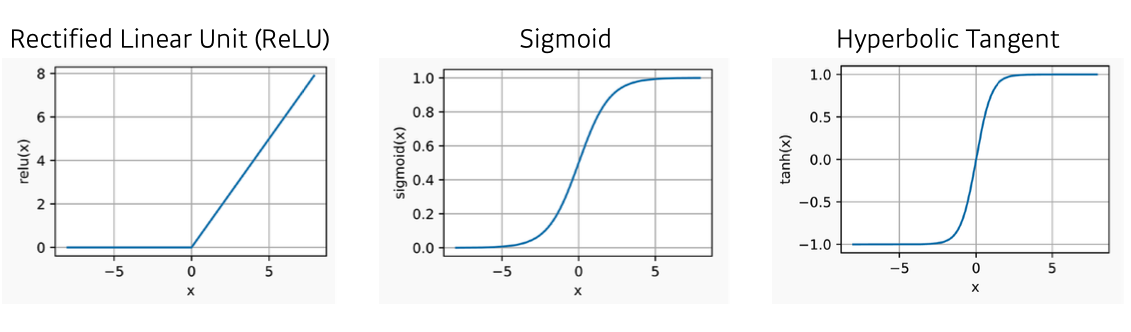
• 대표적인 비선형 함수는 다음과 같다.
  

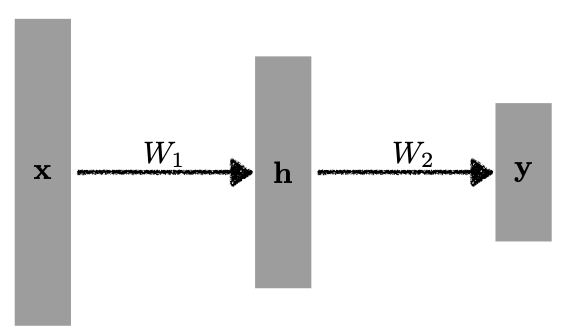
• 이렇게 사이 사이에 비선형 함수를 추가하여 레이어를 쌓은 구조를 Multi Layer Perceptrons이라고 한다.
  

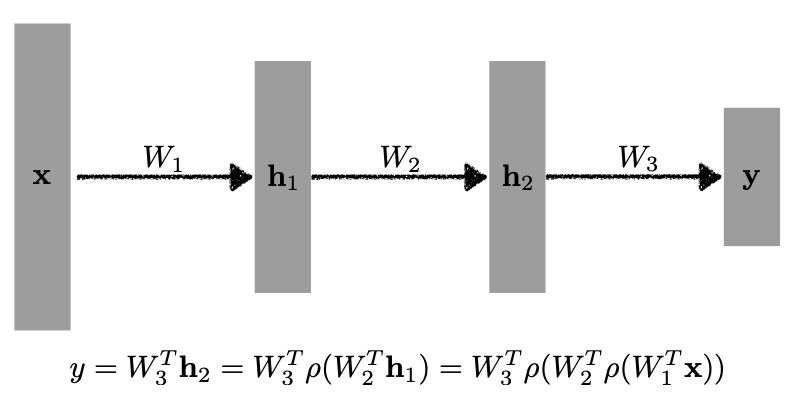
• 물론, 더 깊게 쌓을 수도 있다.

2) Loss function

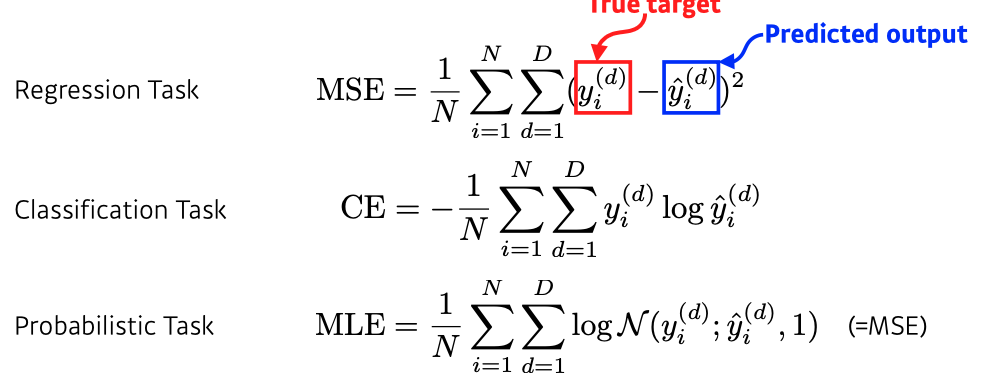
• Regression Task
  • 주로 Mean Square Error를 사용
• Classification Task
  • 정답 클래스가 다른 값에 비해 값이 높기만 하면되고, 값 자체는 크게 상관 없는 경우
  • 주로 Cross Entropy를 사용
• Probabilistic Task
  • 주로 Maximum Likelihood Estimation 사용
• 각 loss function의 성질과 왜 해당 loss function이 특정 Task의 목적을 달성할 수 있는지를 알고 있어야 한다.
  
  

회고 및 과제

• 왜 regression task에서는 주로 MSE를 쓰고,
• 왜 Classification task에서는 CE, Probabilistic에서는 MLE를 사용하는지에 대한 내용 정리하기