<Reference>
https://www.youtube.com/watch?v=odpjk7_tGY0
Generative Model의 Goal
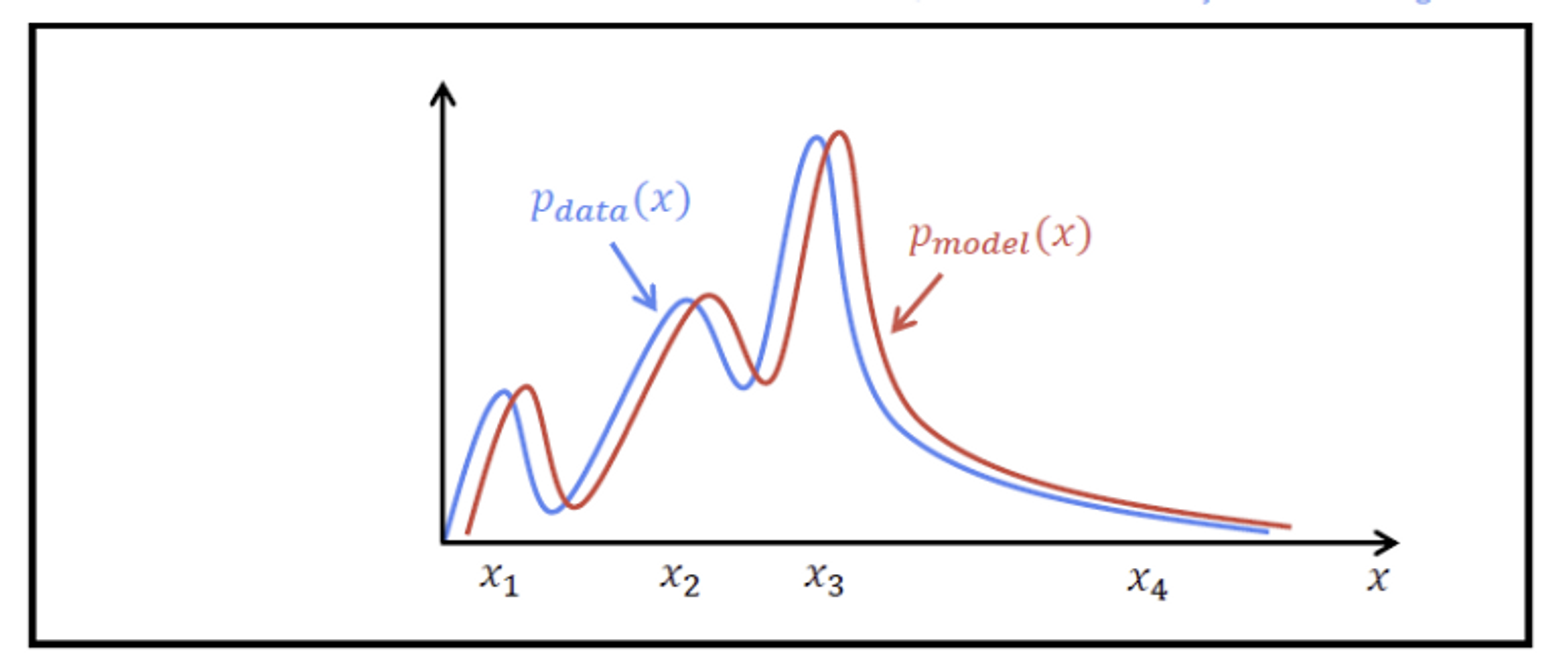
- 에 근사하는 를 찾기
- : 실제 학습 데이터의 분포
- : 모델이 생성한 데이터의 분포
- 두 분포의 차이를 최소화하기
Brief Introduction - GAN(Generative Adversarial Networks)
- (Discriminator Model)
- (Generator Model)
최종 목표는 를 학습하는 것, 이를 위해 를 먼저 학습시킬 필요가 있음
STEP 1) 학습시키기
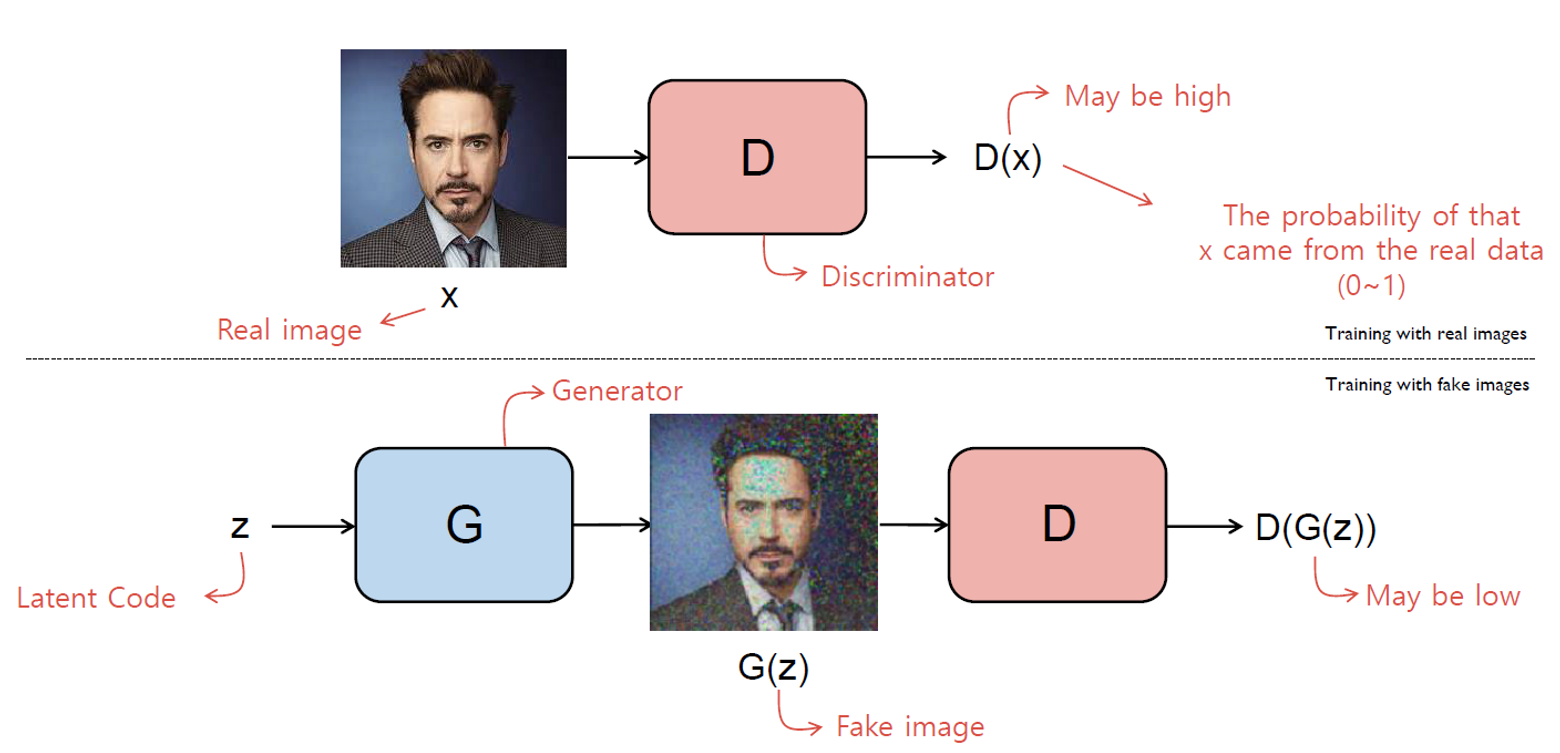
- 진짜 이미지는 1, 가짜 이미지는 0 라벨로 분류하는 것이 학습 목적
- Input : 고정 이미지 벡터
- Output : Binary, 1dim, sigmoid(0.5)
STEP 2) 학습시키기
- 랜덤한 코드(latent code )를 받아 이미지를 생성
- 생성한 이미지로 를 속이는 것이 목표 → 의 output이 1이 되도록
- 학습할 수록 진짜같은 가짜이미지를 생성하게됨
Objective(Loss) Function of GAN
A. Discriminator 관점
- 목적함수를 최대화하는 것이 목적
- Left Term :
- : 확률 밀도 함수, 실제 데이터에서 샘플링,
- 최대화 : 실제 데이터에서 받은 데이터를 입력으로 받으면, 는 1에 가까운 값을 출력해야함, 는 0~1사이 값을 출력
- Right Term :
- : z는 Generator로 들어가는 입력, 표준 정규 분포/uniform 분포에서 랜덤하게 추출된 100차원의 벡터
- : Random 하게 생성한 벡터를 입력으로 받아 Generate한 이미지, 출력은 가짜 이미지
- : 이를 다시 Discriminator에 넣어 Fake, Real Binary classification
- : 값이 0일때 최대 = 로 부터 생성된 가짜 이미지를 가짜로 분류하였을때 최대값을 가짐 = 학습 목표
B. Generator 관점
- 목적함수를 최소화하는 것이 목적
- Left Term :
- 실제이미지를 discriminate하는 것과 Generator는 독립
- Right Term :
- 가짜이미지를 입력으로 받았을 때 Discriminator가 진짜 이미지로 분류하도록 하는 것이 목적
- 값이 1일때 최소 = z로 부터 생성된 가짜 이미지를 진짜로 분류하였을때 최소값을 가짐 = 학습 목표
Pytorch Implementation
DCGAN Tutorial - PyTorch Tutorials 1.13.1+cu117 documentation
import torch
import torch.nn. as nn
D = nn.Sequential(
nn.Linear(784 ,128),
nn.ReLU(),
nn.Linear(128, 1),
nn.Sigmoid())
G = nn.Sequential(
nn.Linear(100, 128),
nn.ReLU(),
nn.Linear(128, 784),
nn.Tanh()) # 생성된 값이 -1 ~ 1
criterion = nn.BCELoss() # Binary Cross Entropy Loss(h(x), y)
d_optimizer = torch.optim.Adam(D.parameters(), lr=0.01) #maximize
g_optimizer = torch.optim.Adam(G.parameters(), lr=0.01) #minimize
# 충돌하기에 2개의 optimizer를 설정
while True:
# train D
loss = criterion(D(x), 1) + criterion(D(G(z)), 0)
loss.backward() # 모든 weight에 대해 gradient값을 계산
d_optimizer.step()
# train G
loss = criterion(D(G(z)), 1)
loss.backward()
g_optimizer.step() # generator의 파라미터를 학습Binary Cross Entropy Loss
criterion = nn.BCELoss()Loss function
loss = criterion(D(x),1) + criterion(D(G(x)),0)criterion(D(x),1):criterion(D(G(x)),0):
**Note : Gradient Descent로 학습되기 때문에 기존 loss function에 -를 붙여준 형태
**Train 에서 주의할 점
- Generator를 학습할 때 Discriminator는 고정이어야함.
- optimizer를 파라미터에 대해 각각 설정해두고, genrator학습 시
g_optimizer.step()만 수행
Non-Saturating GAN Loss
의 objective Function
- 그래프
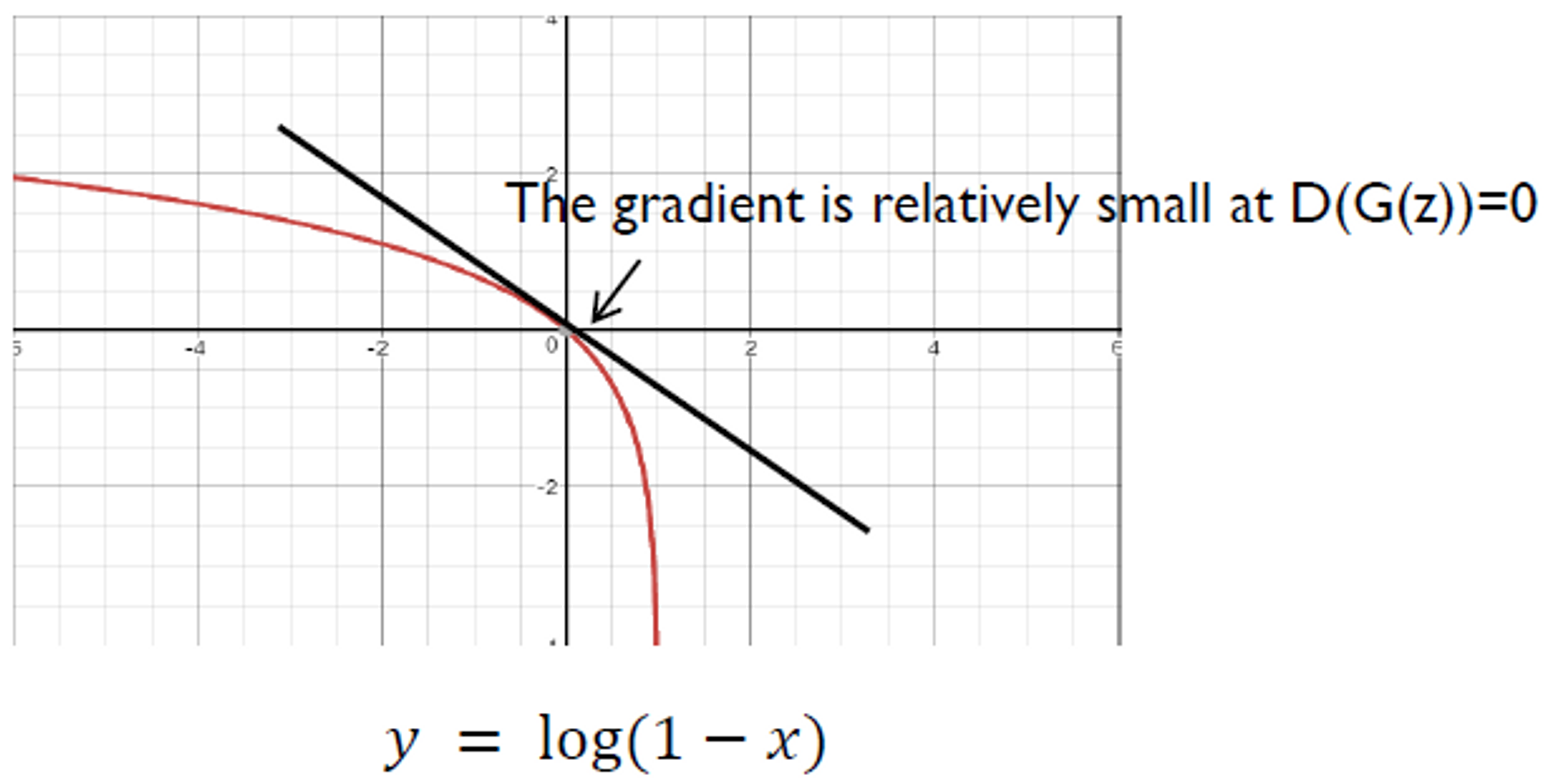
는 학습 초반에 매우 평편없는 이미지를 생성하게 되고, 는 이를 가짜 이미지라고 확신하게됨 → 가 0에 매우 가까운 값을 출력
⚠️ 이때의 gradient가 상대적으로 작다
💡 를 최소화 하는 대신 를 최대화 하자
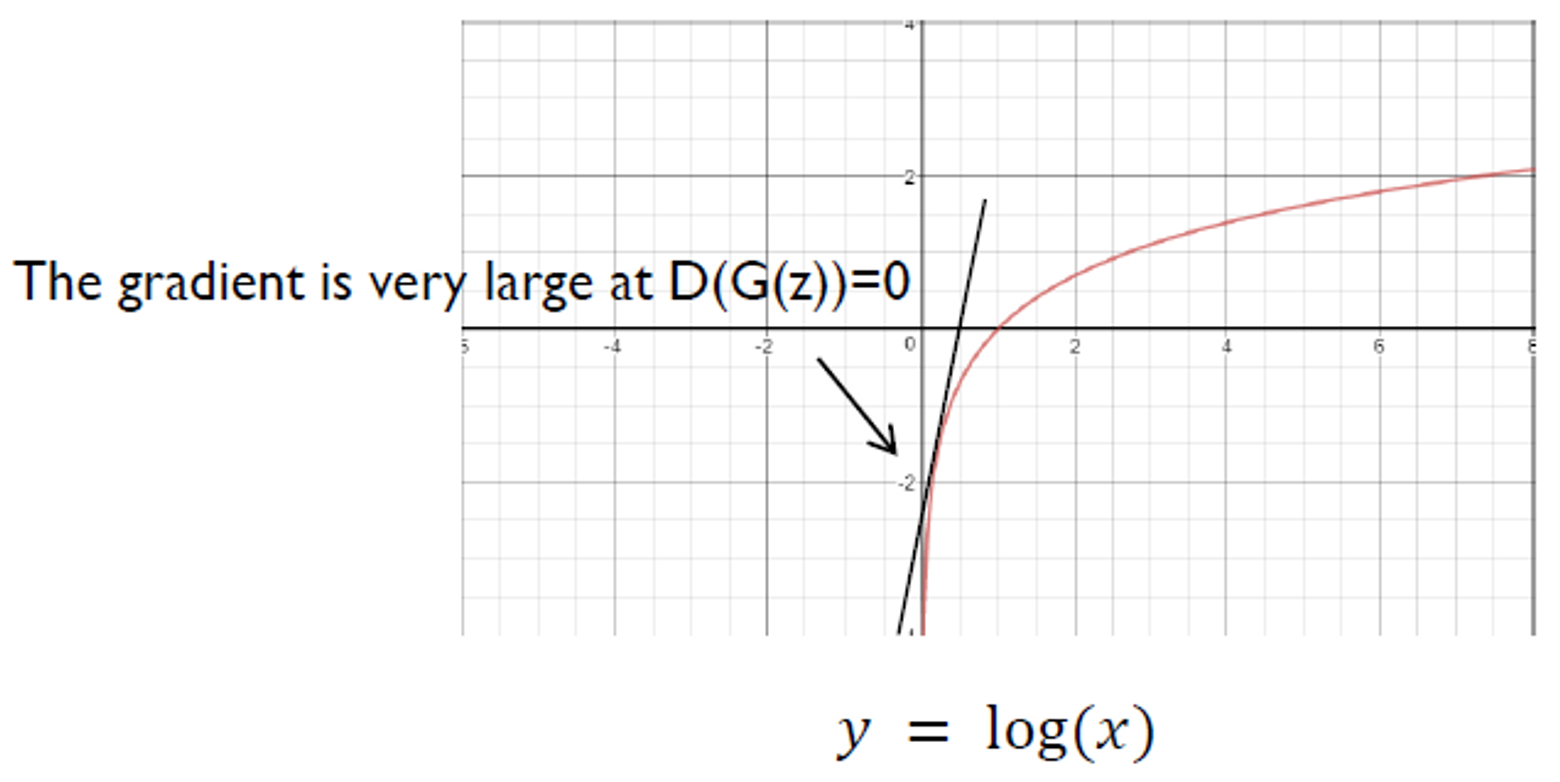
→ 상대적으로 큰 graident
⇒ 초반에 Generator가 매우 안좋은 상황을 최대한 빠르게 벗어날 수 있게됨
Implementation
loss = criterion(D(G(z)), 1)Why does GANs work?
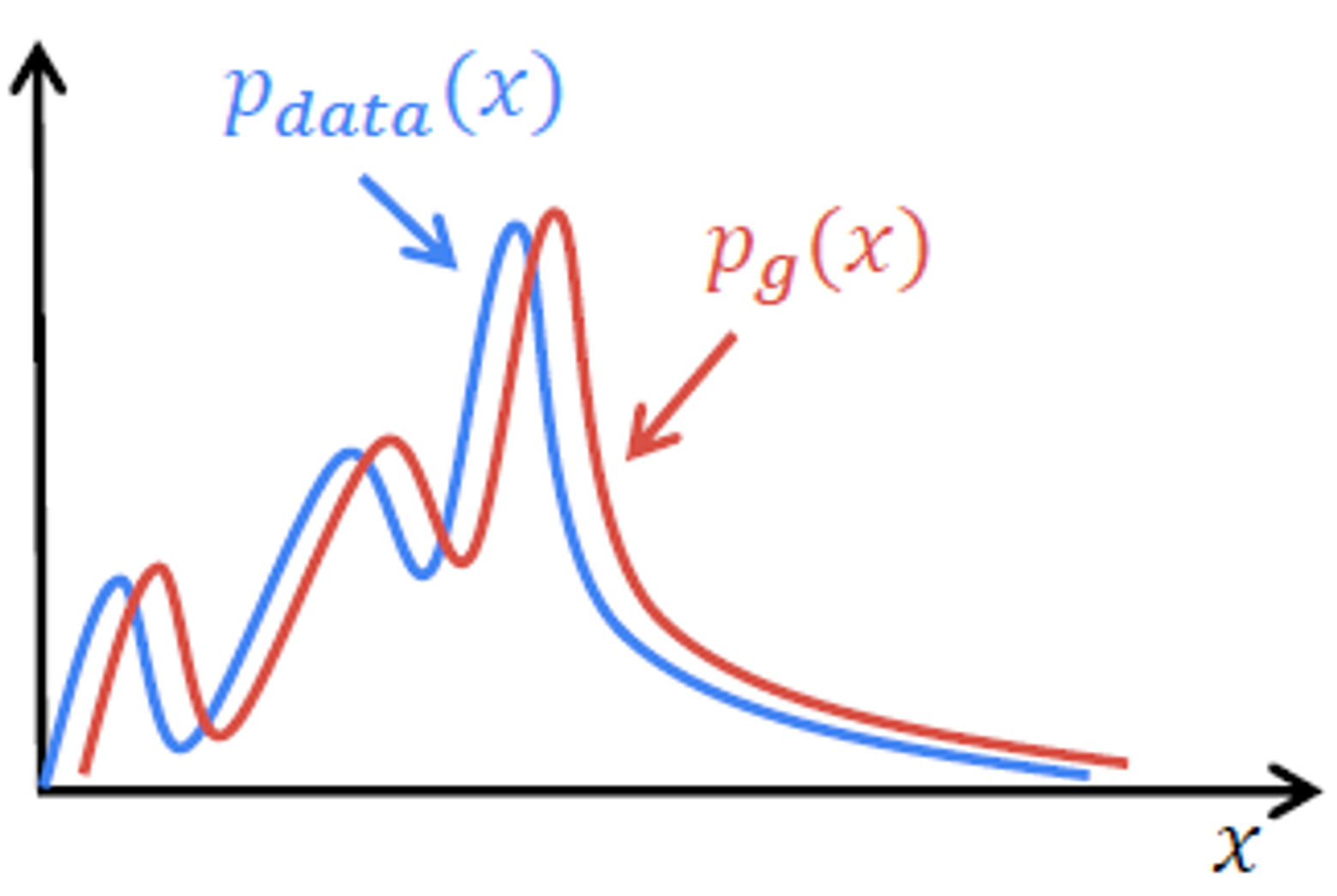
GAN의 loss function을 최대화 하는 것이 실제 데이터와 가짜 데이터의 분포 차이를 줄이는 것이 맞는가? → O
어떤식으로 GAN이 학습되는지 돌아보고 다시 아래에서 증명을 이어서 해보자!
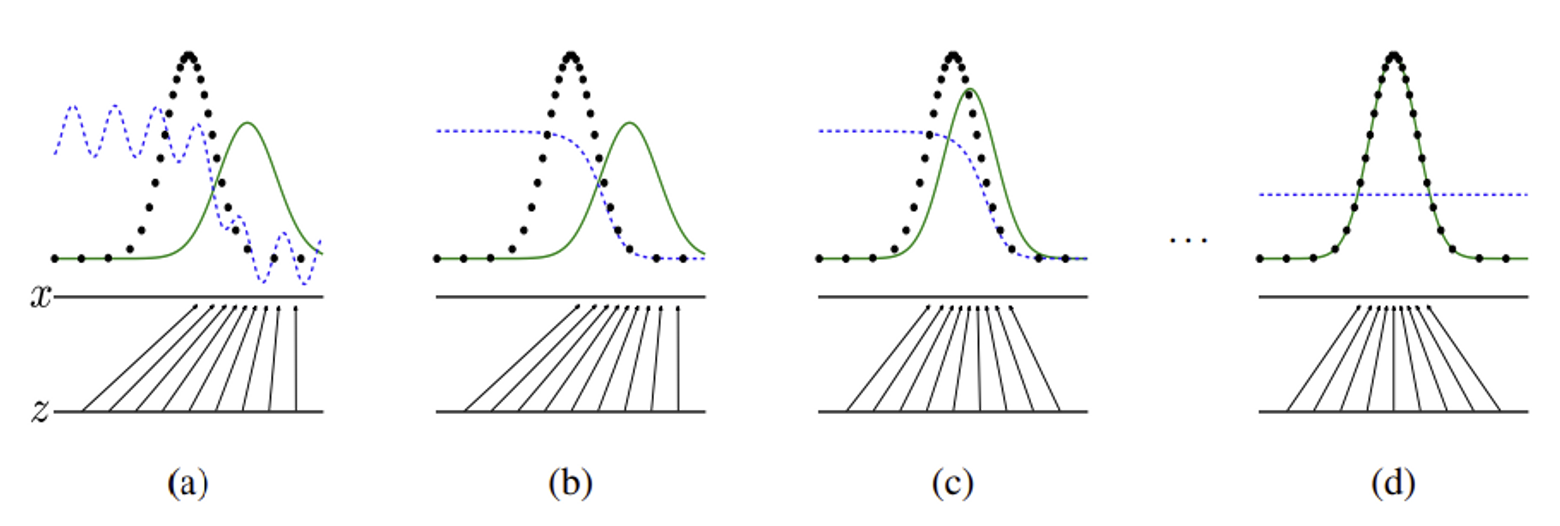
- 파란색 점선 : , discriminative distribution (판별 모델의 분포)
- 검정색 점선 : , 데이터에서 생성된 분포 (원본 데이터의 분포)
- 초록색 실선 : , generative distribution (생성 모델의 분포)
- z 실선 : uniformly sampling된 z의 domain
- z → x 화살표 : 매핑, non-uniform 분포 로 변환되는 과정
- x 실선 : 매핑/변환된 x
GAN은 Discriminative distribution과 동시에 실제 데이터에서 샘플링하여 생성된 분포 와 Generator를 통해 생성된 분포에서 샘플링한 를 구분하도록 학습
contracts in regions of high density and expands in regions of low density of .
(a) 매핑을 통해 만들어진 가짜 분포
(b) 을 통해 판별 모델 확률 분포 업데이트
(c) 가 에 가깝도록 업데이트
(d) 학습을 계속 반복하여 가 되면 두 분포를 구분할 수 없어져 로 수렴
-
어떻게 가 로 수렴할 수 있게 될까?
- Proof. Global Optimality
-
G가 고정되어있는 상황에서 D의 optimal point
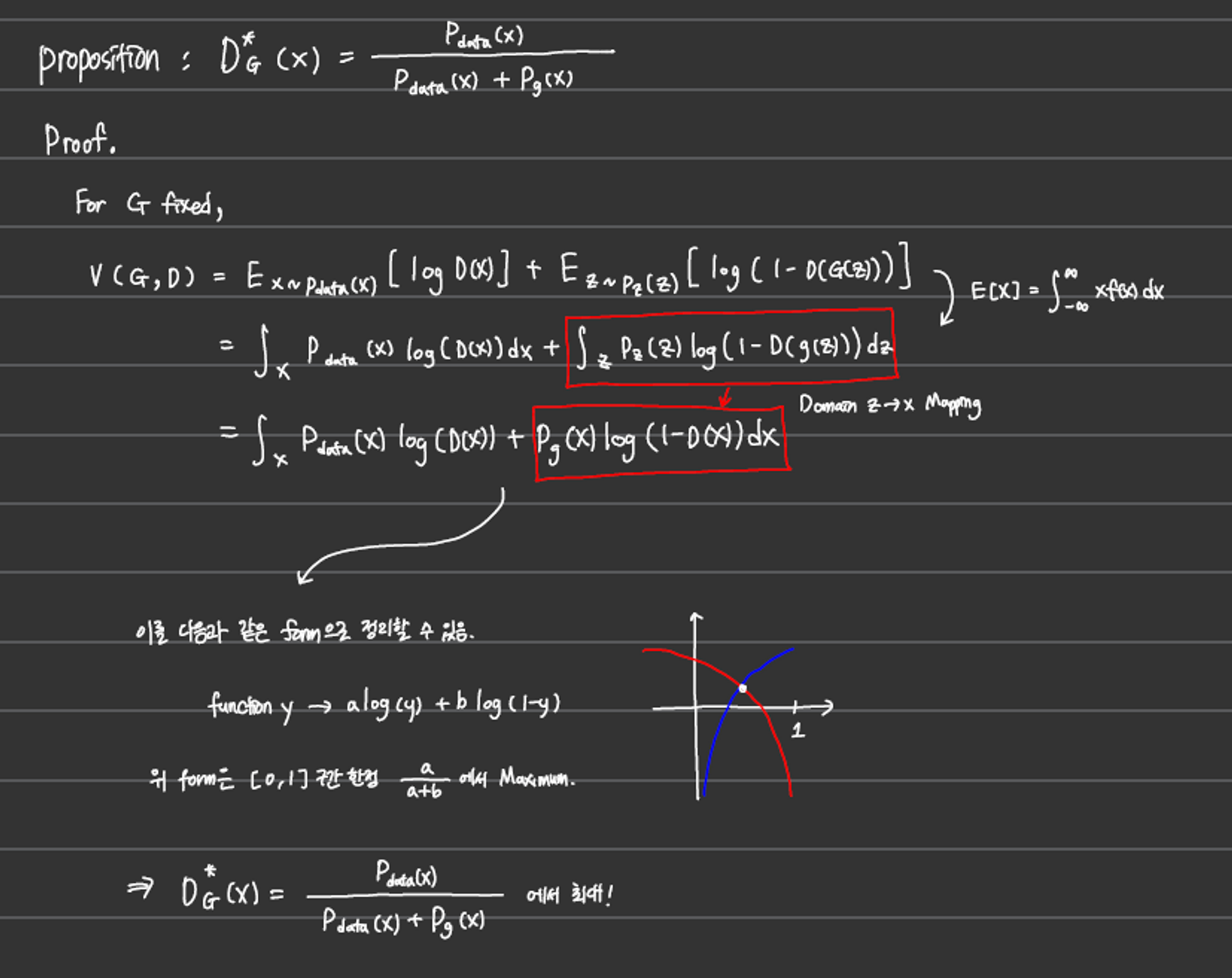
-
G의 global optimum은 에 있다.

-
KL divergence
Note. BCE
- = 희망하는 타겟에 대한 결괏값
- = 모델에서 출력한 출력값
- Q라는 모델의 결과에 대해 P라는 이상적인 값을 기대했을 때 그와 실제 결과의 차이에 대한 감각
확률분포 를 모델링한다고 할때, 이산 확률 분포 와 가 동일한 샘플 공간 에서 정의된다고 하면 KL divergence는 다음과 같다.
이를 기댓값()으로 치환하면
*여기서 는 라는 확률 분포에 대한 기댓값 연산임을 의미
이를 전개하면
*여기서 는 를 기준으로 봤을 때 에대한 cross entropy, 는 에 대한 정보 엔트로피
: 어떠한 확률분포 P가 있을 때, 샘플링 과정에서 확률분포 Q를 P 대신 사용할 경우 엔트로피
: 위에서 를 빼주게 되면, 기존에서의 엔트로피의 변화를 의미하게됨
- 항상 0이상
- aysymmetric : distance개념이 아니다.
-
JSD(Jensen-Shannon Divergence)
KL divergence를 distance metric으로 쓸 수 있는 방법은 없을까
을 확률 분포 와 의 평균이라고 할 때
- symmetric → distance개념
Algorithm

Variations of GAN
1. DCGAN(Deep Convolutional GAN)
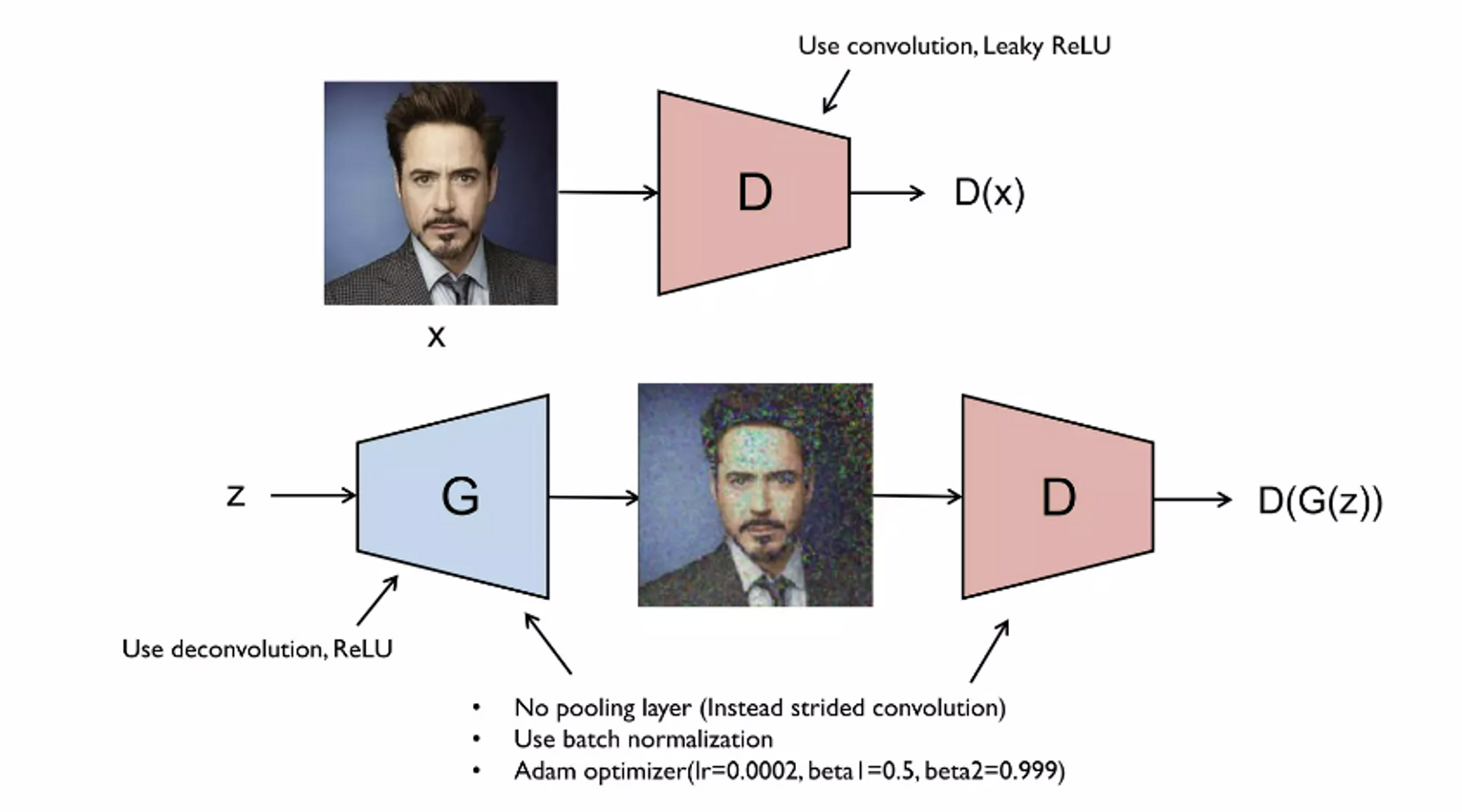
- Discriminator
- CNN
- Generator
- deep convolutional NN
- deconvolution, transpose convolution → upsampling
- No pooling layer
- stride size>2 의 convolution,deconvolution
- BN
- Adam optimizer
- Momentum = 0.5, 0.999
- 64x64이미지를 사용할때 실험적으로 위 숫자들을 사용할 때 성능이 좋은 것을 확인
- Generator의 입력인 Latent vector 간의 산술적 연산이 가능! (선형적 관계)
- ex. man with glasses - man without glassed + woman without glasses ⇒ woman with glasses
2. LSGAN(Least Squares GAN)
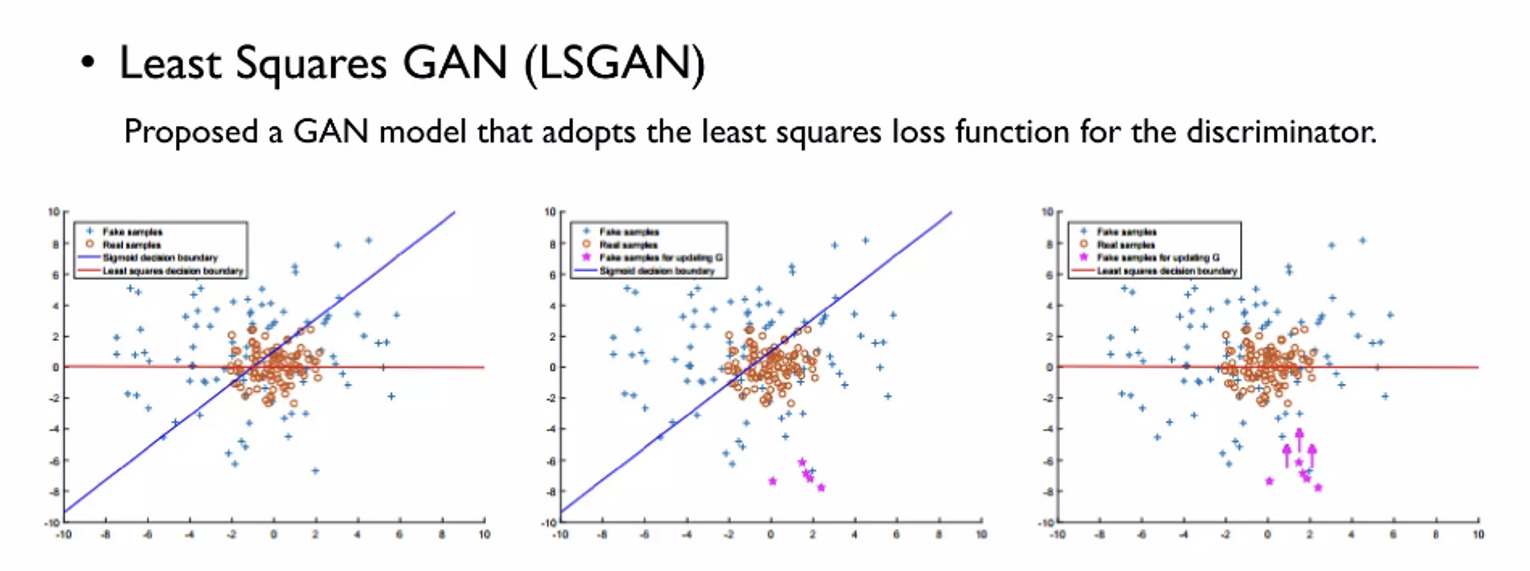
- 기존의 GAN Loss → 를 속이기만 하면 됨
- 파란색 선 = 의 decision boundary → 낮으면 진짜, 높으면 가짜
- 빨간색 점들 → 진짜 이미지
- 파란색 점들 → 가짜 이미지
- ⇒ 빨간점에 가까이 있는 파란 점들은 잘만든 가짜 이미지
- 핑크색 점들 → discriminator를 완벽히 속인 가짜 이미지 (Decision boundary완전 안쪽에 있어서)
💡 그렇다고 핑크색 점들이 잘 만들어진 이미지인가? ⇒ NO
🤷 why? ⇒ 실제 이미지에 가깝게 만들어진게 잘 만들어진 이미지, discriminator를 완벽히 속였어도, 실제와 비슷하다는 보장을 할 수가 없다.
⇒ LSGAN에서는 핑크색 점들을 decision boundary근처로 끌어 올린다.
Vanilla GAN → LSGAN
- 의 마지막 레이어 sigmoid 제거
- 는 동일
- Cross entropy loss ⇒ Least squeares loss
- LSGAN - loss of D
- (D(x)-1)**2 → 진짜 이미지 D(x)는 1에 가깝게
- (D(G(z))**2 → 가짜 이미지 D(G(z))는 0에 가깝게
- LSGAN - loss of G
- (D(G(z))-1)**2 → 가짜 이미지 D(G(z))는 1에 가깝게
- cross entropy loss와의 차이 :
- 1에 최대한 가까운 값이 나오도록 조정하게됨
*Note. 코드로 비교해보자~!
- Vanilla GAN
import torch
import torch.nn. as nn
D = nn.Sequential(
nn.Linear(784 ,128),
nn.ReLU(),
nn.Linear(128, 1),
nn.Sigmoid())
G = nn.Sequential(
nn.Linear(100, 128),
nn.ReLU(),
nn.Linear(128, 784),
nn.Tanh())
#Loss of D
D_loss = -torch.mean(torch.log(D(x))) - torch.mean(torch.log(1-D(G(z))))))
#Loss of G
G_loss = -torch.mean(torch.log(D(G(z))))- LSGAN
import torch
import torch.nn. as nn
D = nn.Sequential(
nn.Linear(784 ,128),
nn.ReLU(),
nn.Linear(128, 1)) #1. Remove sigmoid
G = nn.Sequential(
nn.Linear(100, 128),
nn.ReLU(),
nn.Linear(128, 784),
nn.Tanh())
#Loss of D
D_loss = -torch.mean((D(x)-1)**2) - torch.mean(D(G(z))**2))
#Loss of G
G_loss = -torch.mean((D(G(z))-1)**2)3. SGAN(Semi-Supervised GAN)
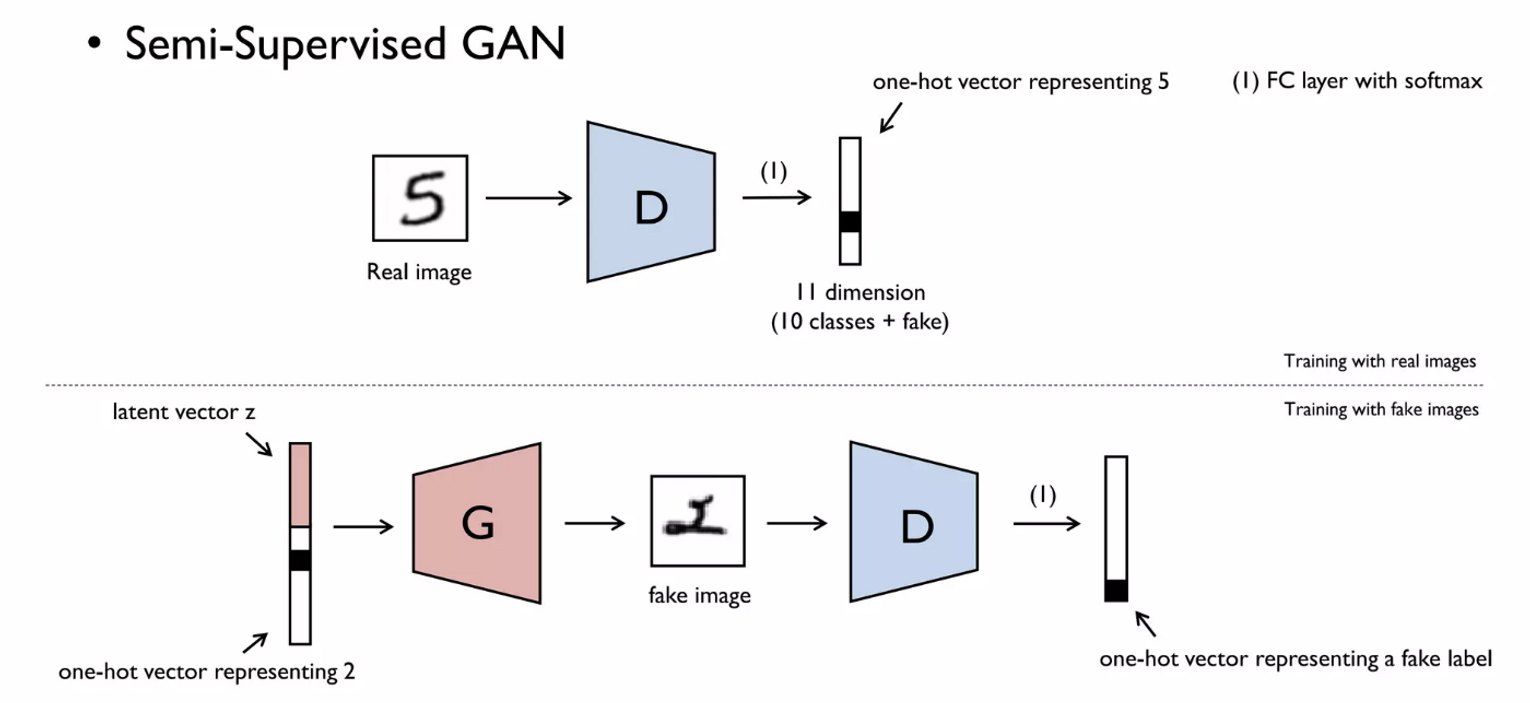
- MNIST data
- 가 진짜/가짜를 구분하는 것이 아닌 class를 구분(0~9) + Fake class를 추가해 11개의 class ⇒ softmax ⇒ one-hot vector
- 는 one-hot vector + latent vector 를 input으로 받아 fake image생성
- 는 이 이미지는 fake로 분류해야함
- 는 라벨이 있어야 하는 supervised learning, 는 generator가 만든 이미지로 분류하는 unsupervised learning ⇒ Semi-Supervised GAN
4. ACGAN(Auxiliary Classifier GAN)
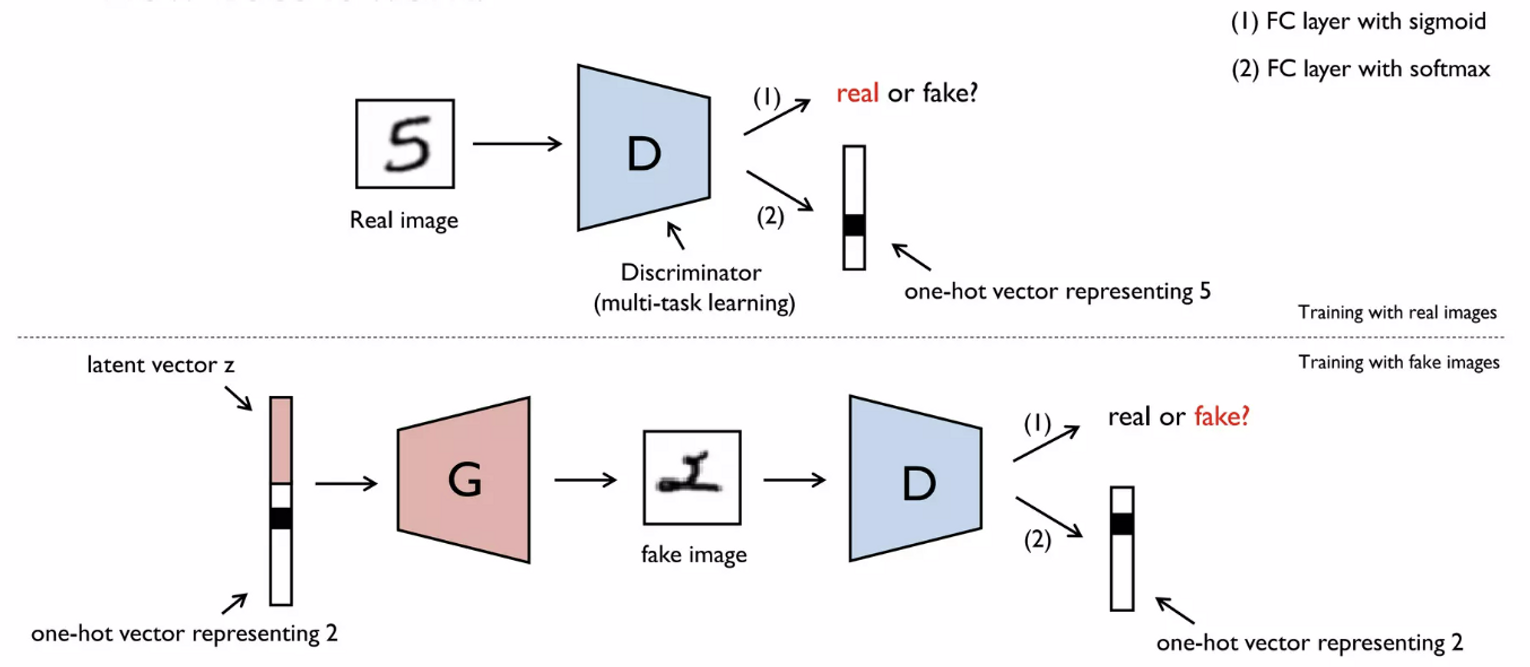
- → Multi-task learning
- 진짜이미지 vs 가짜이미지 (0 or 1) → sigmoid
- 이미지의 진위 여부와 관계 없이 0~9중 어떤 숫자에 해당하는지 → softmax
- 노이즈가 포함된 이미지의 분류에 집중
- input = one-hot vector + latent vector
- 여기서 생성한 가짜 이미지로 는 다음 두가지 task 시행
- 진짜이미지 vs 가짜이미지 (0 or 1)
- 이미지의 진위 여부와 관계 없이 0~9중 어떤 숫자에 해당하는지
- Data augmentation의 효과 (Noise가 포함된 이미지)
⇒ Loss의 경우 두가지 task의 loss합한 것을 사용
Extensions of GAN
1. CycleGAN : Unpaired Image-to-Image Translation
- 이미지의 style, domain을 바꾸는 task
💡 Pair image가 없는 unsupervised 상태에서도 이러한 task의 학습이 가능하지 않을까?
⇒ How does it work?
ex. 얼룩말 이미지를 말로 변환하기
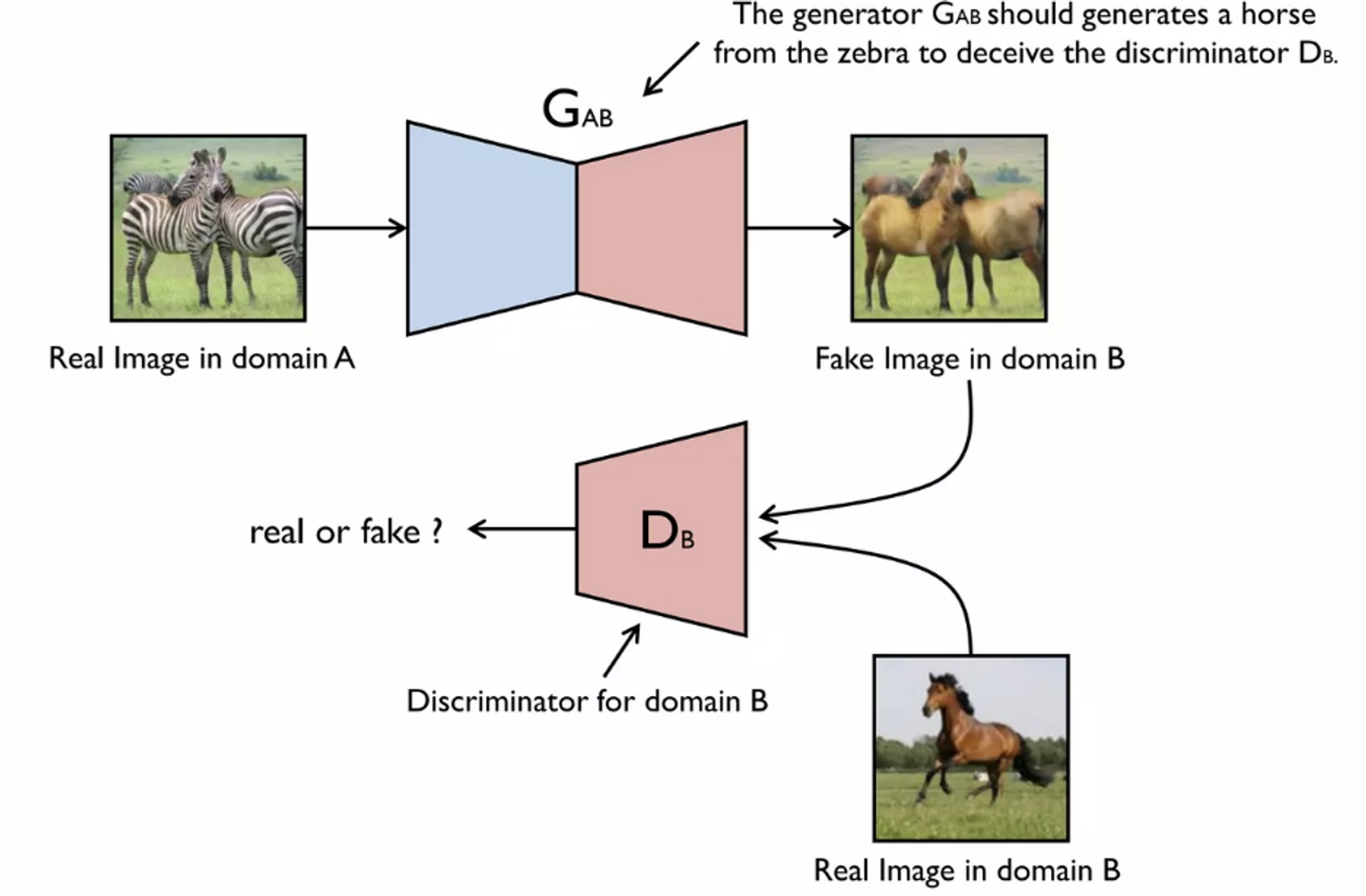
- 말 이미지만 받게 되고, 진짜라고 학습
- latent code 대신 Real image입력을 받게됨
- 차원을 줄였다가 다시 복구하는 encoder decoder 구조
- 얼룩말 이미지를 받아 를 속이기 위해 말 모양으로 변환
**Note. 얼룩말 이미지를 말로 변환하되, 이미지의 형태는 유지해야함!
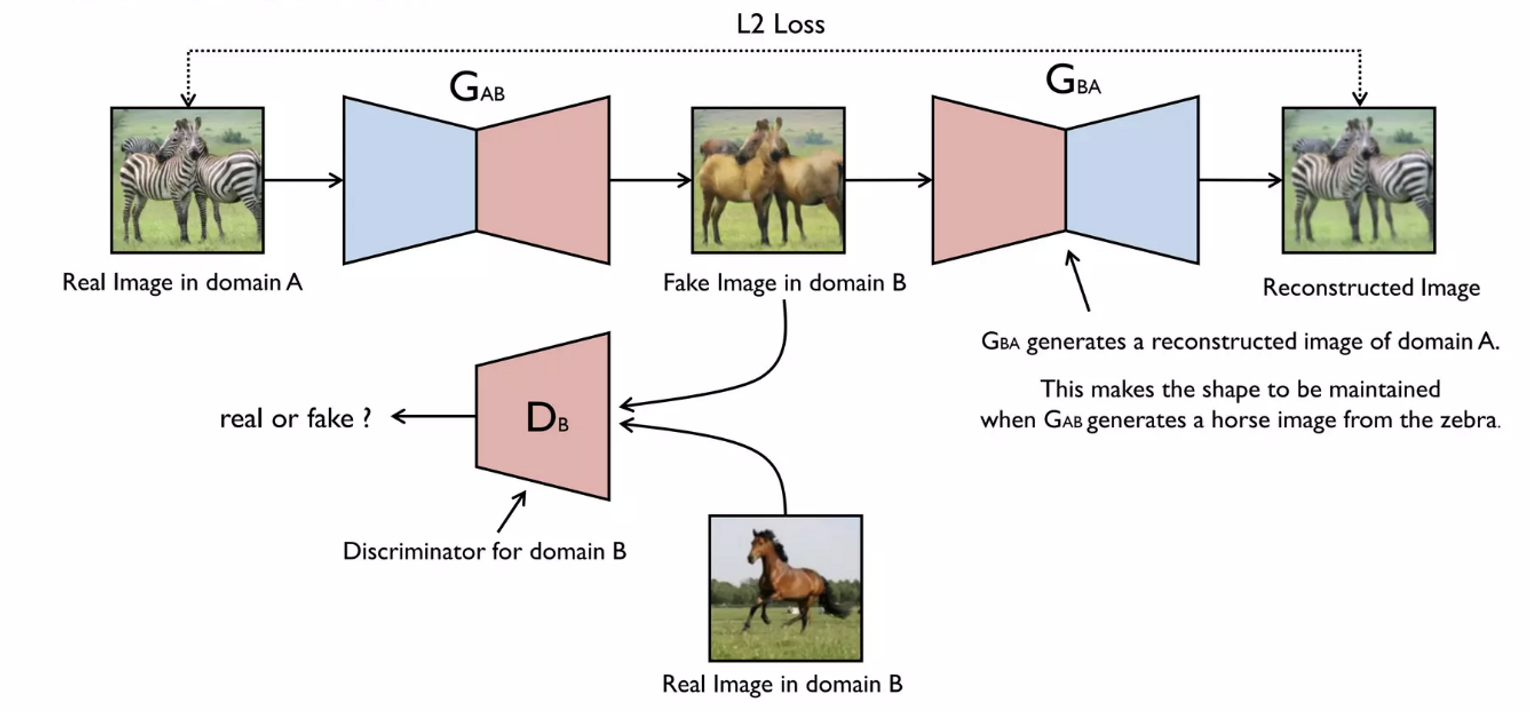
- 로 다시 원래 이미지로 복원하려면 모양이 최대한 적게 바뀌어야함 → reconstrunction error를 줄이는 방향
Implementation
https://github.com/yunjey/mnist-svhn-transfer
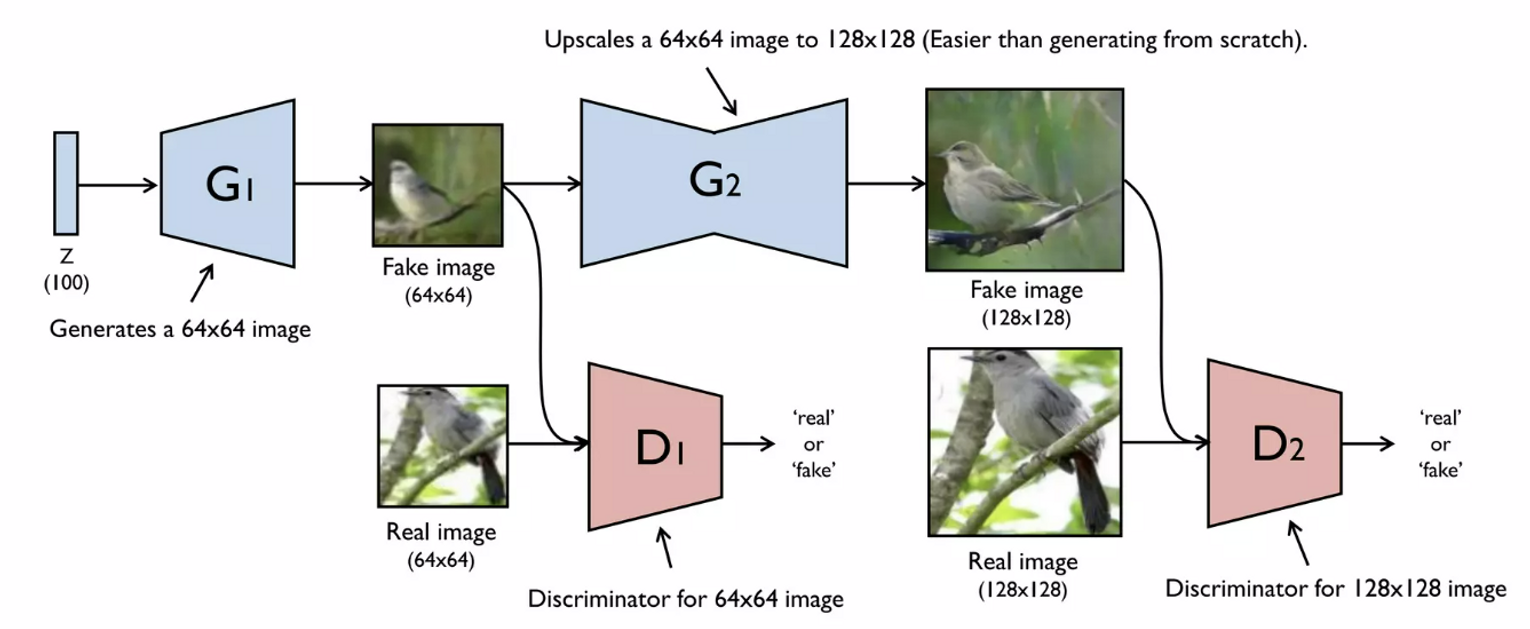
2. StackGAN : Text to Photo-realistic Image Synthesis
- text를 주고 그에 해당하는 이미지 생성
⚠️ 128x128, 256x256 고해상도 이미지를 벡터에서 바로 생성하기 어렵다는 문제
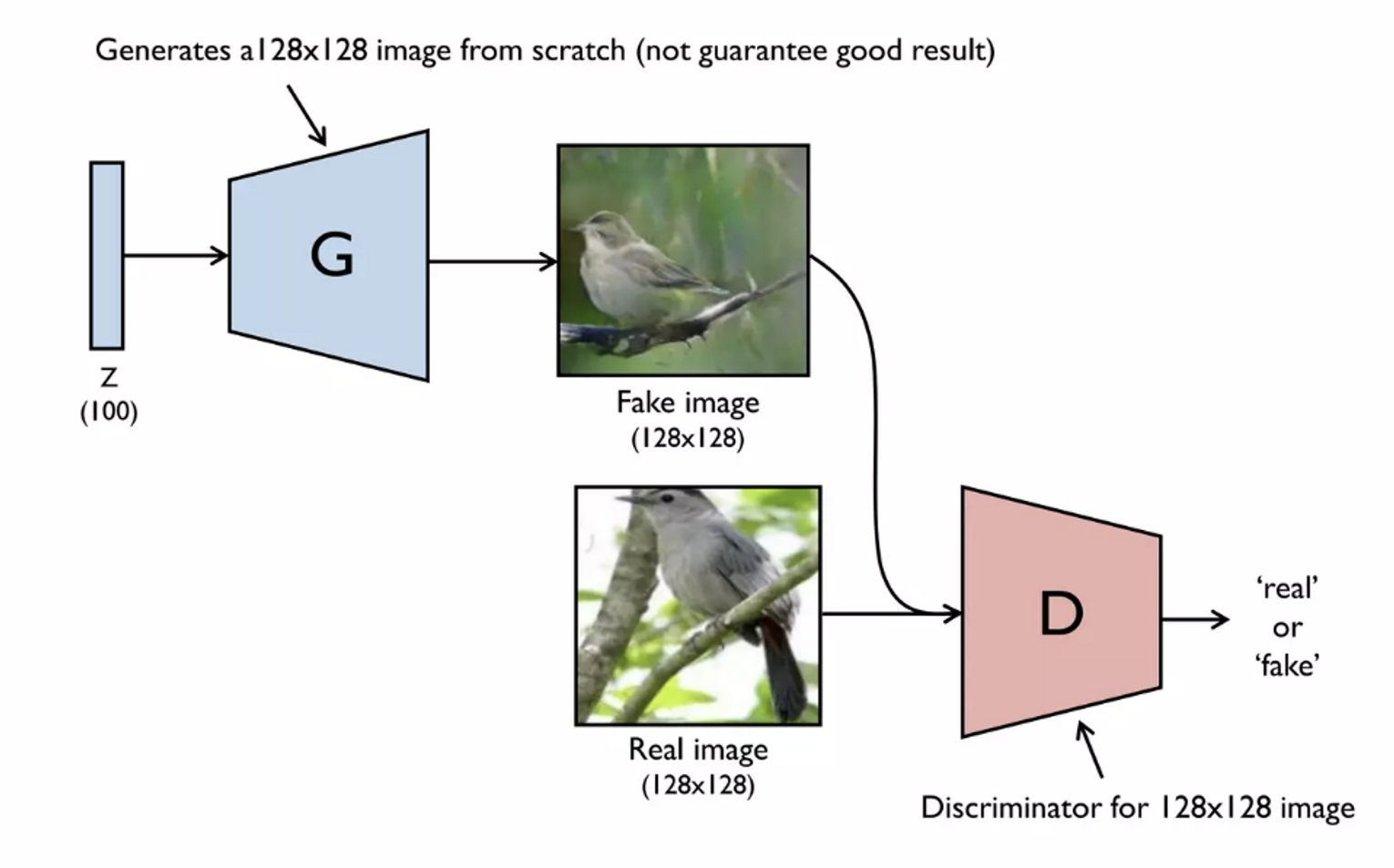
💡 64x64 저해상도 이미지를 먼저 생성한 후 이를 기반으로 또다른 Generator로 upsampling하기