[Python] 머신러닝 완벽 가이드 # 13. 다항 회귀, 편향-분산 트레이드 오프

✏️ 13. 다항 회귀, 편향-분산 트레이드 오프

다항 회귀(Polynormial Regression)

• 다항 회귀는 𝑦 = 𝑤0 + 𝑤1𝑥1 + 𝑤2𝑥2 + 𝑤3𝑥1𝑥2 + 𝑤4𝑥1**2 + 𝑤5𝑥2**2과 같이 회귀식이 독립변수의 단항식이 아닌 2차, 3차 방정식과 같은 형태로 표현되는 것을 지칭한다

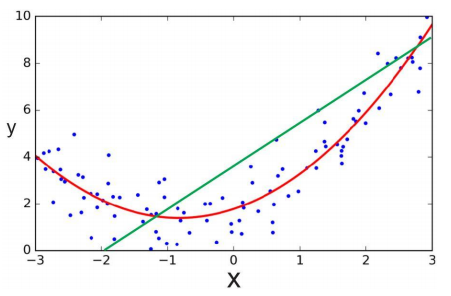
• 데이터 세트에 대해서 Feature에 대해 Target 값의 관계를 단순 선형 회귀 직선으로 표현한 것 보다 다항 회귀 곡선으로 표현한 것이 더 예측 성능이 높다.

선형 회귀와 비선형 회귀의 구분

• 선형 회귀

  • 𝑦 = 𝑤0 + 𝑤1𝑥1 + 𝑤2𝑥2 + 𝑤3𝑥1𝑥2 + 𝑤4𝑥1**2 + 𝑤5𝑥2**2 에서 만약 새로운 변수인 𝑍를 𝑍 = [𝑥1, 𝑥2, 𝑥1𝑥2, 𝑥1**2, 𝑥2**2]로 정의한다면 𝑦 = 𝑤0 + 𝑤1𝑧1 + 𝑤2𝑧2 + 𝑤3𝑧3 + 𝑤4𝑧4 + 𝑤5𝑧5 로 표현되기 때문에 다항 회귀가 곡선으로 표현된다고 해서 비선형 회귀인 것은 아니다.

  • 즉 다항 회귀는 선형 회귀 이며 회귀에서 선형 회귀 / 비선형 회귀를 나누는 기준은 회귀 계수가 선형 / 비선형인지에 따른 것이지 독립 변수의 선형 / 비선형 여부와는 무관하다.

• 비선형 회귀

  • 𝑦 = 𝑤1 cos 𝑥 + 𝑤4 + 𝑤2 cos(2𝑥 + 𝑤4) + 𝑤3 cos 함수를 이용해 각각의 계수 𝑤가 묶여 있기 때문에 비선형 회귀이다

사이킷런 다항회귀

• 사이킷런에는 다항회귀 API가 존재하지는 않기 때문에 PolynomialFeatures 클래스를 이용해 원본 단항 피처를 단항 피처로 변환해 LinearRegression을 적용시켜야 한다.

• 단항 피처 [𝑥1, 𝑥2]의 차수(degree)를 2차 다항 피처로 변환시키면 (𝑥1 + 𝑥2)**2의 식 전개에 대응되는[1, 𝑥1, 𝑥2, 𝑥1𝑥2, 𝑥1**2, 𝑥2**2]의 다항 피처로 변환된다.

  • 1차 단항 피처가 𝑥1, 𝑥2 = [0, 1]이라면 2차 다항 피처는 [1, 𝑥1 = 0, 𝑥2 = 1, 𝑥1𝑥2 = 0,𝑥1 2 = 0, 𝑥22 = 1] 형태인 [1, 0, 1, 0, 0, 1]이 된다.

과대적합, 과소적합

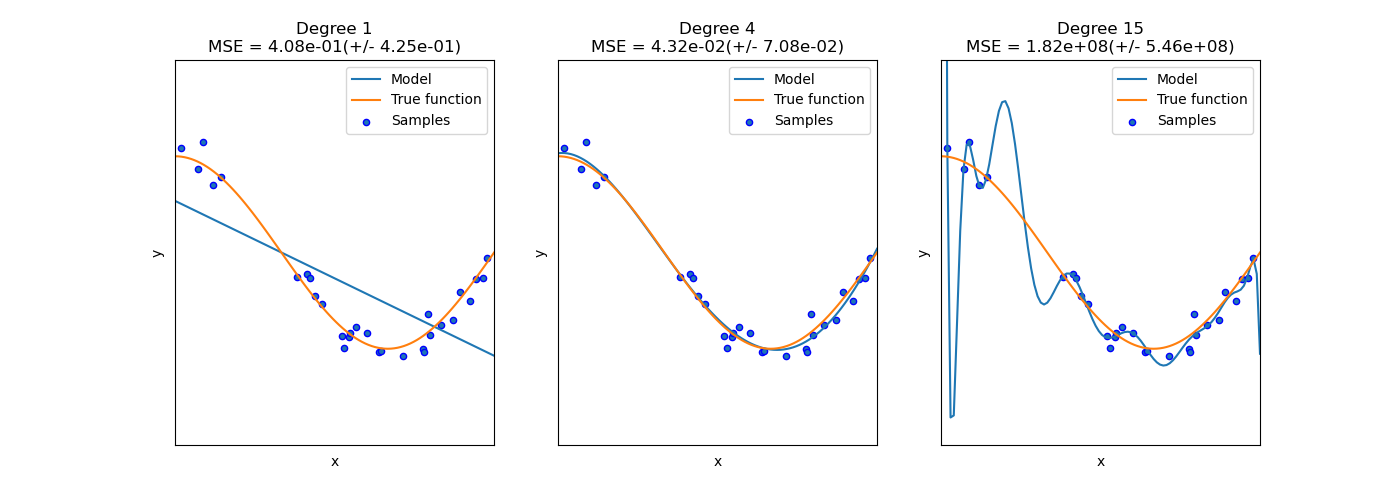
• Degree 1: 그림은 방향성만 고려하고, 실제 데이터를 고려하지는 못한다. (과소적합)

• Degree 4: 그림은 데이터의 방향성과 실제 데이터를 적절히 고려한다. (일반화)

• Degree 15: 그림은 모델의 변동성이 매우 심하다. 즉 데이터를 너무 과하게 해석한다. (과대적합)

• 과소적합은 문제를 굉장히 단순하게 보기 때문에 약간만 문제가 복잡해져도 해결하지 못한다.

• 과대적합은 단순한 문제를 고차원으로 풀기 때문에 훈련 데이터에 대해서는 잘 맞을지 모르나, 테스트 데이터에 대한 성능은 매우 떨어질 수 있다

편향-분산 트레이드 오프

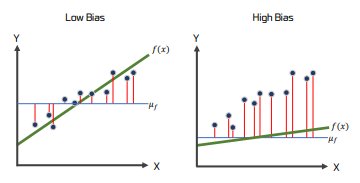
• Bias(편향)는 훈련 데이터에 대한 방향성, 예측이 정확하게 방향성을 잘 잡고 가고 있는가를 의미한다.

• 훈련 데이터와 모델 예측의 차이. 즉 에러를 의미한다.

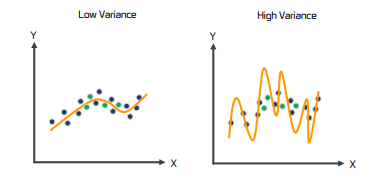
• Variance(분산)은 테스트 데이터를 예측 할 때 마다 초점에서 얼마만큼 벗어나는가를 의미한다.

• 즉 훈련 데이터 예측에 대한 분산이 커지면, 테스트 세트의 예측이 잘 안된다.

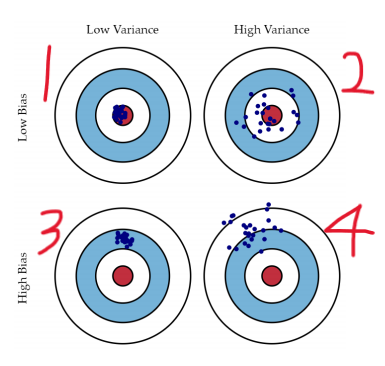
1. Best인 상황. 방향성과 예측하고자 하는 초점이 정확하게 맞는다

2. 머신러닝 모델을 만들었을 때 많이 만나볼 수 있는 상황이다. 방향성은 괜찮지만 예측 시 이리저리 산만하게 분산되는 것을 알 수 있다. 이 상태가 바로 과대적합 상태이다.

3. 예측 방향이 잘못 됐으나, 테스트 할 때마다 비슷하게 값이 모여 있는 경우이다. 예측 전 세팅이 잘못 되어 있는 경우이다

4. 방향성, 예측의 초점이 모두 엉망이다. 즉 데이터를 하나도 반영하지 못하는 과소적합 상태라고 볼 수 있다

• 일반적으로 편향이 높으면 분산은 낮아지고 편향이 낮아지면 분산이 높은 경향이 많다.

• Degree 1: 1차원 직선으로 예측했기 때문에 예측의 분산이 낮다. 하지만 편향이 높다. (과소적합)

• Degree 4: 데이터의 방향성과 실제 데이터를 적절히 고려한다. (일반화)

• Degree 15: 모든 데이터 포인트를 예측을 하였기 때문에 편향은 낮으나 모델 예측의 분산은 높다 (과대적합)

모델 복잡도에 따른 편향-분산 트레이드 오프

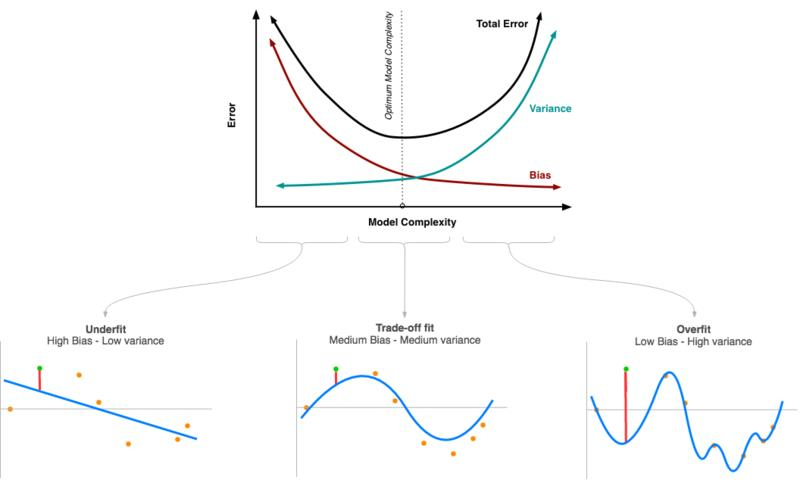
1. Underfit: 모델의 복잡도가 낮은 상태. 모델이 훈련 데이터를 잘 파악하지 못하고 있는 상태이다. 편향이 크고(방향성이 맞지 않고) 분산은 낮은(모델은 단순한) 과소적합 상태를 뜻한다.

2. Trade-off fit: 모델이 최적의 편향과 분산을 찾은 상태이다.

3. Overfit: 모델이 훈련 데이터를 과하게 해석한 상태이다. 편향은 낮으나(방향성은 제대로) 분산이 매우 높아(모델이 매우 복잡함) 과대적합 상태를 뜻한다.

📌 참고 문헌

• 책

  • 📕 파이썬 머신러닝 완벽 가이드 / 권철민

• 참조 자료

  • 🔗 https://scikit-learn.org/stable/modules/linear_model.html

• 해당 챕터의 실습 및 예제 코드는 아래 링크의 Machine Learning 참조 해주시면 됩니다.

  • ✍️ DataSci-Notes