알고 있는 것을 정리해놓지 않으니까 수학적인 것을 계속 잊는 문제가 발생해서 정리의 필요성이 느껴져서 쭉 정리해보려고 한다.
고윳값(eigenvalue)
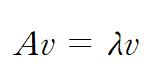
위 식을 만족하는 실수 λ를 고유값이라하고, 벡터 v를 고유 벡터라고 한다. 이러한 고윳값과 고유벡터를 찾는 작업을 eigen-docomposition이라 한다. 이에 대한 것은 너무 잘 알려져 있기 때문에 생략한다.
대각화(diagonalization) / 고유값 분해 (eigenvalue decomposition)
대각화란 주어진 행렬을 대각행렬로 만드는 것을 얘기하며 일반적으로 square matrix(정방행렬)에서 사용된다.
이러한 대각화를 하는 방법 중 하나가 고유값 분해이다.
고유벡터행렬 V는 고유 벡터를 열 벡터로 옆으로 쌓아서 만든 행렬이며, 고윳값 행렬 Λ은 고윳 값을 대각 성분으로 가지는 대각 행렬이다. 일반적으로 가장 큰 값이 Λ_ii에서 i가 작은 위치에 위치한다. 또한 고유벡터 행렬은 normalize해서 나타낸다.
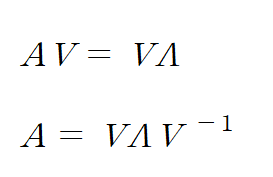
고유벡터 행렬 V의 역행렬이 존재한다면 다음과 같이 대각화가 가능하다고 한다.
이러한 역행렬이 존재하기 위해서는 고유벡터가 선형독립이어야 한다. (고유벡터가 항상 선형독립x, 고윳값이 모두 다를 경우에는 항상 선형 독립)
대칭행렬의 고유 분해
https://deep-learning-study.tistory.com/414
- 행렬 A가 대칭이면 서로 다른 eigenspace에 있는 어떤 두 고유 벡터는 직교 증명
- 행렬 A가 대칭이면 digonalizable(대각화 가능)에 대한 증명
앞으로 표기를 A가 아닌 M으로 표기하며
M은 m * n의 non-singular matrix이다.
∑ 는 특잇값 행렬, Λ 는 고윳값 행렬이다.
SVD
SVD는 Singular Value Decomposition으로 행렬을 특정한 구조로 분해하는 방식 중 하나이다.
고유값 분해의 일반화 버전으로 정방행렬이 아닌 non-singular matrix를 분해할 때 자주 사용한다.
Notation
https://ko.wikipedia.org/wiki/%ED%8A%B9%EC%9E%87%EA%B0%92_%EB%B6%84%ED%95%B4
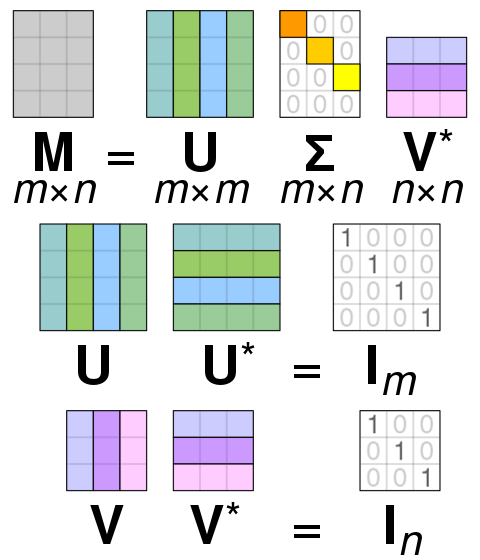
M이라는 행렬이 있을 때 다음과 같이 분해하는 것이 목표이다.
이는 Computer Vision 분야에서 Rotation이나 Translation이 결합된 Matrix M으로부터 Rotation과 Translation을 구하기 위해서 주로 사용된다. (혹은 데이터 압축이나)
이때 u와 v를 각각 좌측 특이벡터와 우측 특이벡터라고 부른다.
여기서 M*의 경우 켤레 전치를 의미한다. 실수 행렬의 경우에는 단순히 전치를 의미한다. 따라서 일반적인 경우 전치 행렬이라고 생각하면 된다.
특잇값 분해(SVD)에서 ∑(diagonal matrix)의 대각선 성분들은 M의 특잇값이 되고 U와 V의 열들은 각각의 특잇값에 해당하는 좌측 특이 벡터와 우측 특이벡터가 된다.
∑은 특이값이 큰 순서대로 낮은 i 순서대로 (∑ _ ii)에 들어간다.
U와 V는 특잇값에 해당하는 벡터들은 Orthogonal matrix로 normal vector이며 dot 연산시 0이라는 특징을 갖는다.
또한 transpose의 결과가 inverse matrix가 된다.
Singular Value (특이값)
m x n 행렬 M의 특이값은 아래와 같이 구한다.
이는 M가 non-singular matrix이기 때문이다.
이러한 M^T M의 사용하는 이유에 대해서 조금 정리하면
- 정방행렬이며, 대칭 행렬(대각화)의 특성을 이용하기 위해서이다.
- 이러한 행렬을 만들면 선형 근사를 진행할 수 있다.
- non singular 행렬에서도 특이값 분해를 할 수 있기 때문이다.
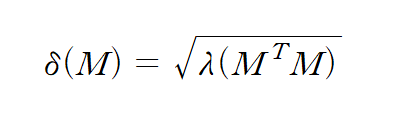
https://math.stackexchange.com/questions/465799/is-matrix-ata-always-symmetric
M^T M가 항상 symmetric matrix에 대한 증명
고윳값과 특잇값을 헷갈리지 말자!
좌측 특이값과 우측 특이값
위에서 설명한 U는 MM^T를 고유값 분해로 직교대각화하여 얻은 m*m 직교 (고유벡터)행렬이며, 이러한 열들을 좌측 특이벡터라고 부른다. (MM^T에서는 u는 동시에 고유 벡터이기도 함)
반대로 V는 M^T M을 고유값 분해로 직교대각화하여 얻은 n*n 직교 (고유벡터)행렬이며, 이러한 열들을 우측 특이벡터라고 부른다. (M^T M에서는 v는 동시에 고유 벡터이기도 함)
이러한 직교 행렬이 성립하는 것은 M^T M과 MM^T가 대칭행렬이므로 고유분해 시 고유 벡터는 직교하기 때문이다. (위의 증명 참고)
SVD의 존재 증명
번외) 특이값 분해와 고유값 분해의 관계
M에서 A로 표기를 잘못 바꿔 작성했다. 여기서 A를 M으로 생각하면 된다.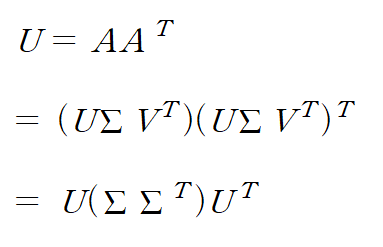

U와 V는 orthogonal matrix이므로 U^T U = V^T = I 이다.
또한 ∑^T∑ = ∑∑^T는 A^TA와 AA^T의 고유값과 같다.
즉, SVD를 계산하는 것은 A^TA와 AA^T의 고유 벡터와 고유값을 구하는 것과 같다는 뜻이다.



