Essential Matrix, Fundamental Matrix

Essential Matrix

컴퓨터 비전에서 Essential Matrix는 3x3 matrix로, pinhole camera model을 만족한다고 가정할 때 유사성을 가지는 두 이미지 사이의 matching feature들을 연결하는, epipolar constraint를 만족하는 행렬이다.

여기서 Essential Matrix는 카메라 사이의 회전과 거리 값에 대한 정보를 담고 있다.
이는 거리 값(t)를 cross product의 Matrix 형태에 Rotation Matrix를 곱한 형태와 같다. 역으로 Essential Matrix를 SVD 분해하면 Rotation과 t를 구할 수 있다.

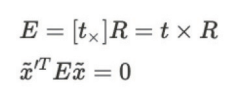
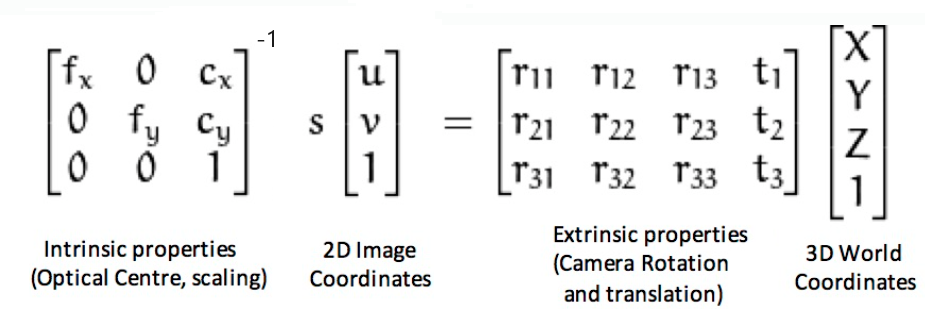
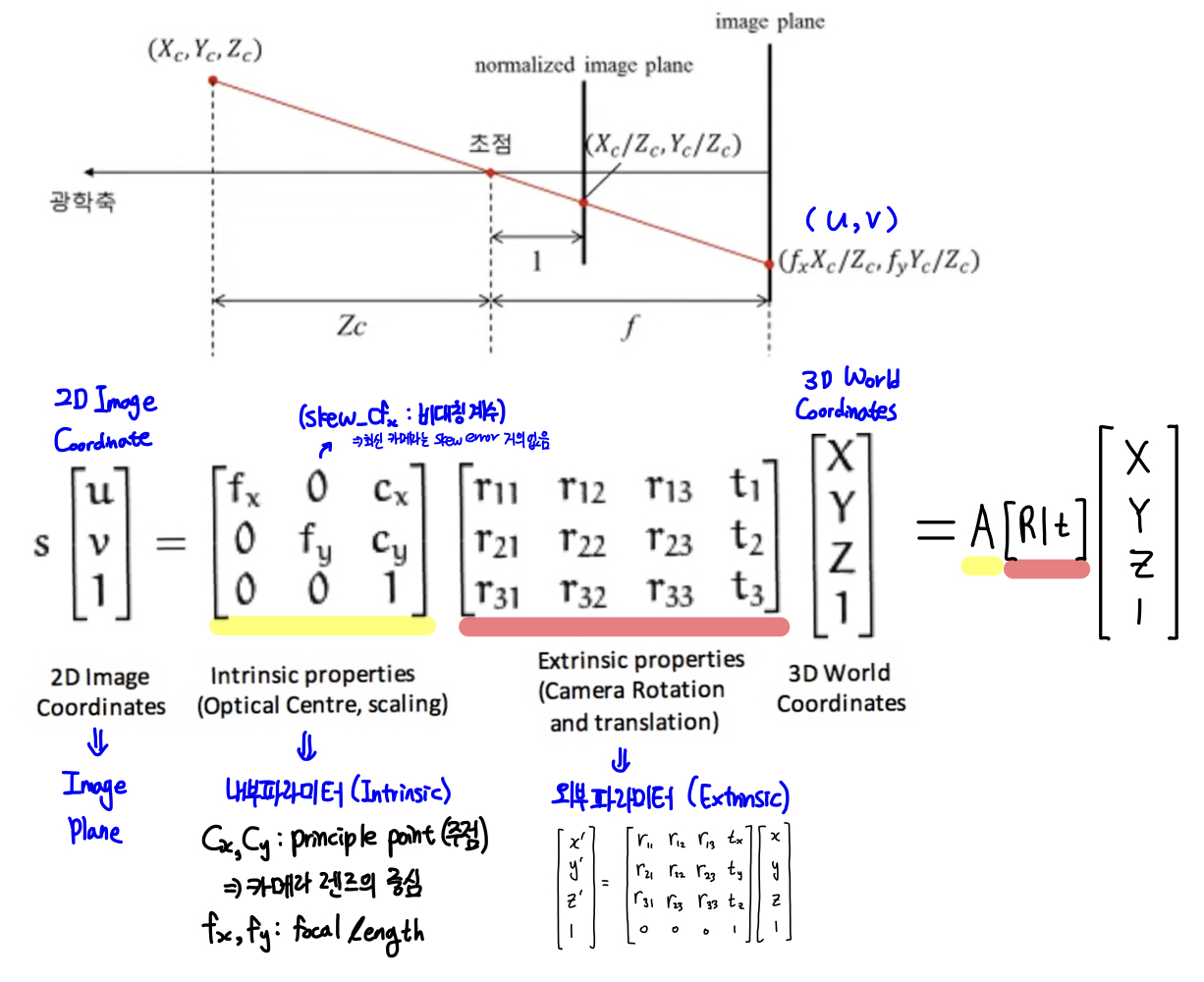
Essential Matrix에서 x는 픽셀 좌표계가 아니라, homogenous normalized image coordinates (-1~1으로 이뤄진 평면 값)을 이용하기 때문에 각 x에 intrinsic matrix, K의 역수를 곱해줘서 픽셀 좌표계에서 homogenous normalized image coordinates로 만들어줘야 한다.

Fundamental Matrix

이러한 내부 파라미터의 역행렬과 Essential Matrix를 포함하고 있는 것이 Fundamental Matrix이다.

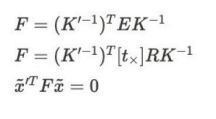
Essential Matrix가 normalized image coordinates 간의 매칭된 점들에 대한 Matrix라면, Fundamental Matrix의 경우 매칭된 필셀 점들에 대한 Rotation과 Translation에 대한 Matrix로 변경되게 된다.

특정 픽셀의 위치를 Fundamental Matrix에 곱하게 되면 반대편 이미지에서의 epipolar line이 나오게 되는데 line에 대한 벡터에 픽셀 벡터를 곱하면 0이 나오게 된다.

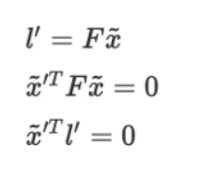
이러한 결과가 나오게 되는 이유는 이미지에서는 깊이 값이 없기 때문에 Fundamental Matrix를 곱하는 과정에서 특정 점이 아닌 line이 나오게 된다.

Coordinates

좌표계를 정리하면 다음과 같다.

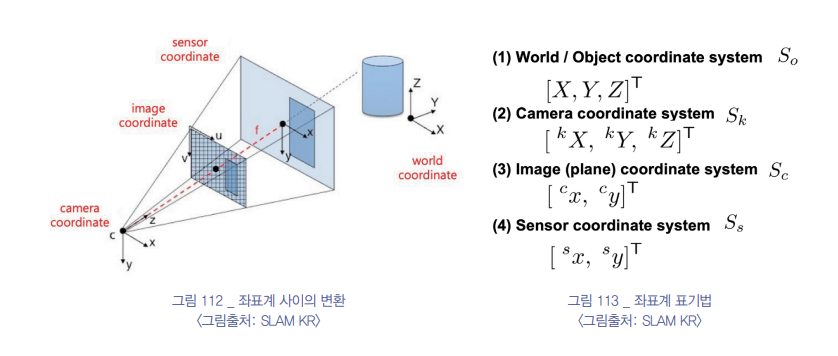
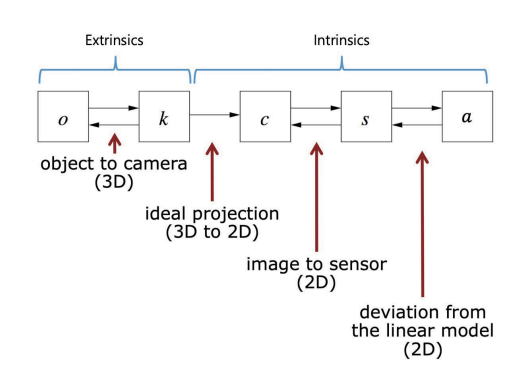
object to camera : world space to camera space
ideal projection : 원근 사영 변환 (Projection) / (-1~1 평면)
image to sensor : 중앙 원점에서 좌측 상단을 원점으로 변환
deviation from the linear model : 렌즈 왜곡 변환

정리하면 intrinsic matrix의 역행렬을 픽셀에 곱한다는 것은, 렌즈 왜곡을 취소하고, 원점을 다시 중앙으로 두는 것을 얘기한다.
원근 사영 변환의 경우 2d->3d로 depth 정보가 없으므로 불가능하다.

Epipolar Constraint

Fundamental Matrix에 픽셀 값을 곱하면 line이 나온다고 했다. (epipolar line) 이러한 line이 나올 수 있게 epipolar constraint를 만든다.

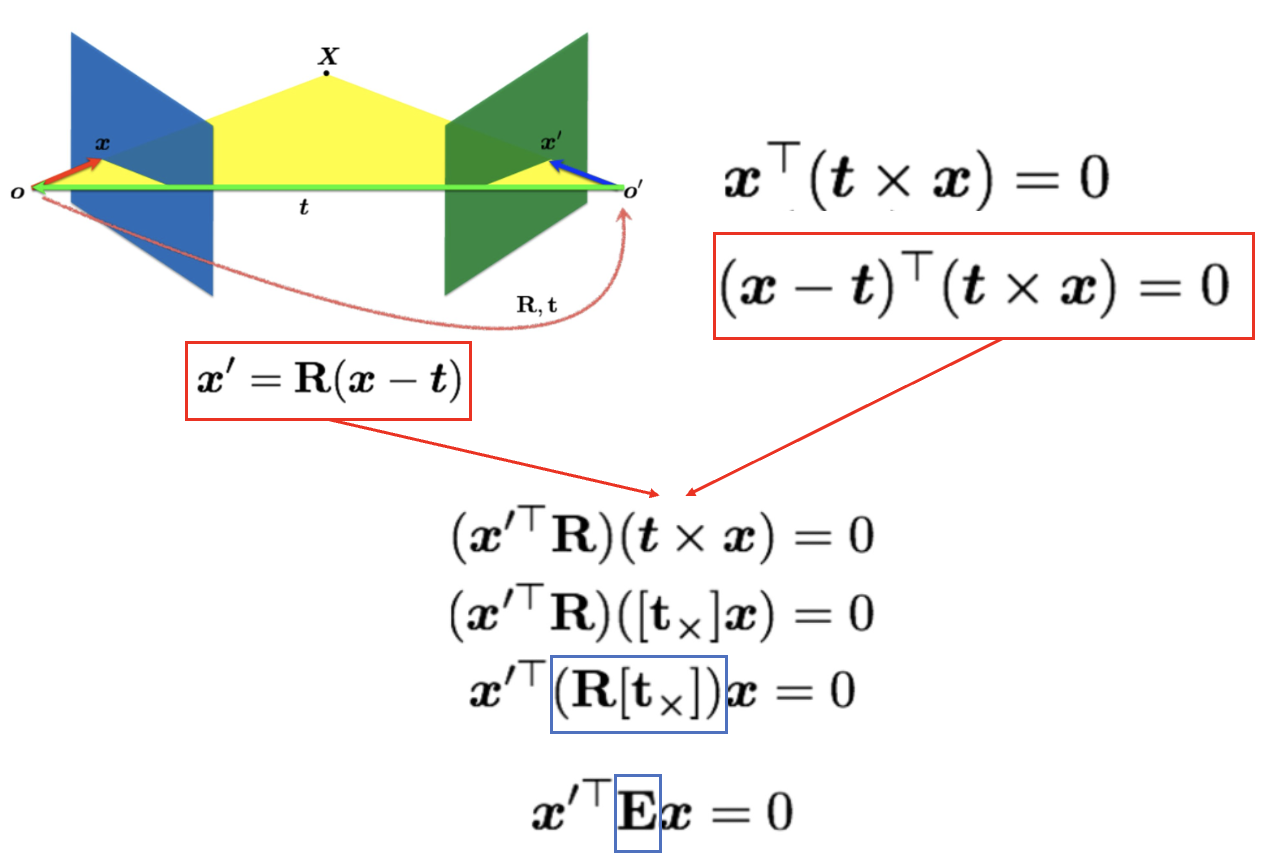
o를 왼쪽 카메라, o'를 오른쪽 카메라라고 했을 때,
1) x'은 왼쪽(o) 카메라에서 특징점 x를 left camera coordinate to right camera coordinate로의 Matrix를 곱한 것과 같다는 점.
2) x와 t가 같은 평면(Epipolar plane)에 있다는 점

1), 2)를 이용해서 Essential Matrix를 구성하고, intrinsic matrix의 역행렬을 양 옆에 곱함으로써 Fundamental Matrix를 구성할 수 있다.

여기서 [t_x]는 다음과 같이 유도되었다.

Estimate Essential Matrix

SVD on Essential Matrix

E를 SVD를 통해서 나타낼 수 있을 것이다. (SVD는 항상 가능)

U와 V는 orthogonal 3x3 matrix이고, Σ는 아래와 같이 3x3 diagonal matrix일 것이다. (RANK 2)

s는 E의 singular value이며, 내재적 constraint에 의해서 다음과 같이 정의된다.

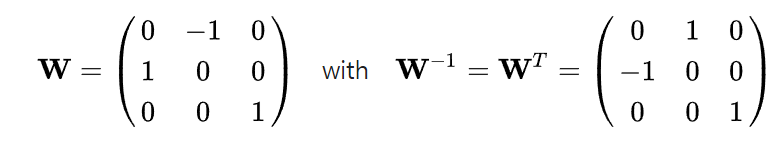
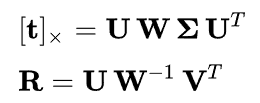
실제 카메라 데이터는 constraint를 완전히 지키지 못하기 때문에 다음과 같이 사용된다.

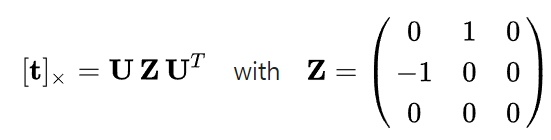
증명

먼저 성립한다는 것을 보여주는 등식이다.

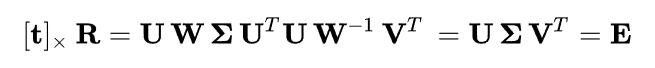
[t_x]는 skew-symmetric이다. 위에서 [t_x]의 유도에서 보여주었 듯이 cross product의 matrix form은 skew-symmetric이고, 따라서 SVD를 진행하여 [t_x]를 얻을 때도 마찬가지로 skew-symmetric을 지켜야 한다.

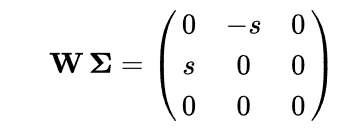
skew-symmetric은 transpose 결과가 음수로 나와야 한다.

따라서 해당 등식이 성립함이 보인다. (마찬가지로 U도 봐야하는데 transpose시 그대로 유지되는 것을 볼 수 있다.)

또한 R은 Rotation matrix가 되어야 한다.

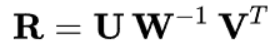
로 설정 시 총 3개의 Matrix가 나온다.
모두 orthogonal 하거나 det(R)=±1 이다.
이중 적절한 matrix는 det(R)=1 인 것이다.

그런데 이게 또 항상 가능한 방법은 아니라고 한다...
아래 링크에서 Essential Matrix에 대한 survey로 증명들이 자세하게 적혀있다. 나중에 다시 정복을 해야겠다.

https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.64.7518

Openvslam에서의 essential solver

https://github.com/zm0612/openvslam-comments/blob/main/src/openvslam/solve/essential_solver.cc

bool essential_solver::decompose(const Mat33_t& E_21, eigen_alloc_vector<Mat33_t>& init_rots, eigen_alloc_vector<Vec3_t>& init_transes) {
    // https://en.wikipedia.org/wiki/Essential_matrix#Determining_R_and_t_from_E

    const Eigen::JacobiSVD<Mat33_t> svd(E_21, Eigen::ComputeFullU | Eigen::ComputeFullV);

    Vec3_t trans = svd.matrixU().col(2);
    trans.normalize();

    Mat33_t W = Mat33_t::Zero();
    W(0, 1) = -1;
    W(1, 0) = 1;
    W(2, 2) = 1;

    Mat33_t rot_1 = svd.matrixU() * W * svd.matrixV().transpose();
    if (rot_1.determinant() < 0) {
        rot_1 *= -1;
    }

    Mat33_t rot_2 = svd.matrixU() * W.transpose() * svd.matrixV().transpose();
    if (rot_2.determinant() < 0) {
        rot_2 *= -1;
    }

    init_rots = {rot_1, rot_1, rot_2, rot_2};
    init_transes = {trans, -trans, trans, -trans};

    return true;
}

Eigen::jacobiSVD로 행렬을 SVD 분해를 한다.
(Jacobi는 여러 수학적 방법과 알고리즘에 사용되는 이름으로, 여기에는 Jacobi 반복법을 얘기한다.)

Essential matrix E에 대한 SVD의 특징 중 하나는 특이값이 두 개는 동일하고 하나는 0이다.

t_skew 행렬은 자기 자신의 전치행렬과 음수가 같으므로, 고유값이 0이 되는 고유벡터를 가진다. (실제로는 0이 안 되므로 가장 작은 고윳값에 해당하는 것으로)
(혹은 t_skew 행렬의 고유값을 구하면 항상 0임을 볼 수 있다.)
나머지 두 고유값은 t 벡터에 수직인 평면 상에서의 회전을 표현한다.

수학적으로, 이동 벡터 t는 E의 null space에 있다.
이동 벡터 t가 nullspace에 있는 이유는 Et = 0인데, E가 R*(t_skew)이기 때문에 cross(t,t) = 0으로 t가 nullspace에 있음이 증명된다.
(Σ의 특잇값 2개는 s, 1개는 0이므로 U의 마지막 열은 E의 null space에 해당하며, 이동 벡터 t의 방향을 결정한다.)

SVD에서 U 행렬의 마지막 열은 E의 null space의 기저를 제공합니다. 이는 t의 방향을 나타내지만, 그 크기는 결정하지 않는다. 이러한 이유로 U의 마지막 열을 추출하여 정규화한 것이 실제 이동 벡터 t의 방향을 나타내는 것으로 사용된다.

특잇값 2개가 같은 이유는 다음과 같다.

Skew-symmetric 행렬의 성질로 인해, E의 특이값은 R의 영향을 받는다. 두 스테레오 카메라 시스템이 동일한 장면을 캡처할 때, 필수 행렬 E는 한 카메라에서 본 점을 다른 카메라의 에피폴라 선으로 매핑한다. 이 매핑은 스케일이 지정되지 않은 이동 벡터 t와 회전 R의 결합된 효과인데 이동은 에피폴라 평면에 수직인 방향으로는 측정되지 않는다. 결과적으로, SVD에서 Σ의 대각선 상의 특이값은 두 개가 R에 의해 결정되는 값이 되고, 나머지 하나는 0이 된다.
(t의 크기는 전혀 알 수 없고, 오직 방향만 알 수 있다.)

일반적인 R의 모든 고유값(eigenvalues)은 크기가 1이다. 이는 회전이 벡터의 길이를 보존한다는 것을 의미한다. 회전 행렬의 특이값(singular values)도 고유값과 같은 특성을 가지며, 모두 +1이다.
두 개의 특이값이 같은 값 s를 갖는 이유는 실제 이동 t의 크기가 알려져 있지 않기 때문에 실제 이동 벡터 t의 크기를 알 수 없어서 발생한다. 따라서 임의의 스케일 s로 특잇값이 갖게 된다.

R의 determinant < 0으로 -1을 하는 이유는 다음과 같다.
특별한 경우에는 -1이 될 수 있으나, 이는 좌표계의 방향을 뒤집는 반사(reflection)를 나타내며 일반적인 물리적 회전을 나타내지 못한다. 따라서 determinant > 0으로 통일시켜준다.

R 2개와 translation 2개가 나오는데
(R1,t1), (R1,t2), (R2,t1), (R2,t2)
4가지 조합이 될 수 있다. 이는 물리적으로는 1개만 타당하지만, 수학적으로는 4가지 모두 나올 수 있다.

Rotation이 2개가 나오는 경우를 직관적으로 보면, 두 대의 카메라가 한 장면을 본다고 하자.
이때 두 카메라의 상대적 배치를 "왼쪽에서 오른쪽으로 본 것"과 "오른쪽에서 왼쪽으로 본 것"은 epipolar geometry 상 동일하게 보인다. 즉, 점 대응만으로는 두 배치가 구분되지 않는다.
마찬가지로 trnslation도 카메라가 "앞으로 이동"했는지 똑같은 장면을 "뒤로 이동"하면서 본 건지 한 쌍의 이미지 대응 만으로는 구분 할 수 없다.

3. 최종 해 결정
   그래서 실제로는 cheirality check (positive depth constraint)를 추가로 해야 한다.
   후보 (R, t) 조합으로 3D 점을 복원(triangulation). 모든 점이 카메라 앞에 있으면 올바른 해이고,
   점 일부가 카메라 뒤에 있으면 잘못된 해로 이 검사를 통해 최종 하나의 (R, t)을 확정한다.

모든 4가지 조합에 대해:

• 3D point triangulation 수행
• 두 카메라 좌표계에서의 Z값 (depth)이 양수인지 체크
• 가장 많은 점에서 양의 depth가 나오는 조합 선택

위 방법을 통해서 물리적으로 타당한 값 1개의 조합만 구하면 된다.

참고로 foundamental matrix에서는 바로 decomposition으로 relative pose를 추정할 수 없다.
Essential Matrix는 이미 카메라의 내부 파라미터로 정규화된 좌표계를 기반으로 하여, 기하적으로 "실제 3D 공간에서의 relative pose 정보"를 담고 있기 때문에 가능한 반면, Fundamental Matrix는 정규화되지 않은 픽셀 좌표계 기반으로, 기껏해야 epipolar constraint만 보장할 뿐, rotation과 translation을 분리해낼 수 없다. (카메라 내부 파라미터를 알면 상관없음)

픽셀 좌표는 물리적인 거리나 방향을 보존하지 않는 반면 정규화된 좌표(normalized image coordinates)는 카메라 중심 기준의 방향 벡터이므로, 이들 간의 기하학적 관계(회전/이동)를 3D 공간 상에서 정의 가능하다.

((1000,500) 픽셀이 10∘ 방향인지, 1∘ 방향인지 알 수 없음)

---

Essential matrix (E): 두 카메라가 캘리브레이션(calibration) 되어 있을 때 쓰임. 여기서 복원할 때는 회전(R)과 평행이동(t)을 찾아야 하는데, 수학적으로 4가지 해가 가능하다. (즉 여러 해)

Fundamental matrix (F): 카메라 내부 파라미터를 몰라도 되는 좀 더 일반적인 행렬. 그러나 실제로는 F 자체가 유일하게 결정된다. E를 분해할 때 생기는 모호성이 없고, “두 평면이 교차하는 유일한 직선”처럼 기하적으로 constraint가 더 약해도 행렬 자체는 하나로 수렴한다.
$x_i^T F x_j = 0$
이 제약식은 두 뷰의 대응점 집합으로부터 선형적으로 구할 수 있고, 최소 8쌍의 대응점이 있으면 (8-point algorithm) F는 유일하게 결정된다. 여기서 F는 E와 달리 카메라의 내부 파라미터를 몰라도 되는 관계이기 때문에, “분해(decomposition)” 과정에서 모호성이 발생하지 않는다. 하지만 Essential matrix로 바꿔서 Translation과 Rotation을 구하는 과정에서 똑같은 문제가 발생한다.

Reference

https://nuggy875.tistory.com/168 -> Camera Calibration Image
https://www.cv-learn.com/20230616-slam-book-kr/
https://en.wikipedia.org/wiki/Essential_matrix
https://velog.io/@kimkj38/3D-Geometry-StudyWeek2Epipolar-geometry
http://www.vision.jhu.edu/teaching/vision05/Lecture-D.pdf