트리

Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
(sibling 끼리는 연결될 수 없다)

트리 구성요소

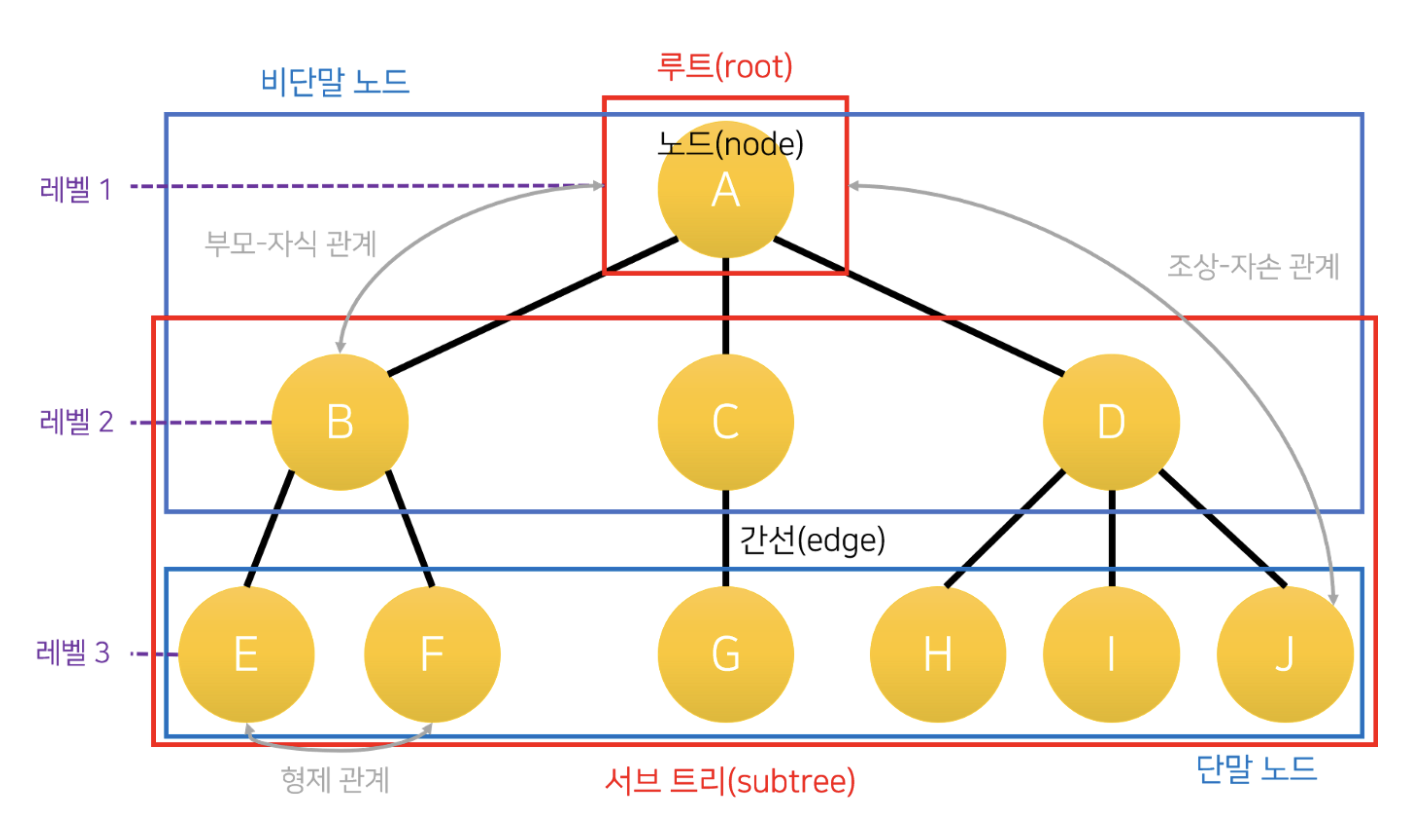
• Node : 트리에서 데이터를 저장하는 기본 요소
• Root Node: 트리 맨 위에 있는 노드
• Level: 최상위 노드를 Level 0 으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
• Parent Node : 어떤 노드의 다음 레벨에 연결된 노드
• Child Node : 어떤 노드의 상위 레벨에 연결된 노드
• Leaf Node(Terminal Node): Child Node가 하나도 없는 노드
• Siblings (Brother Node): 동일한 Parant Node를 가진 노드
• Depth : 트리에서 Node가 가질 수 있는 최대 Level
  (최상단의 레벨는 0 또는 1이 될 수 있다)

이진트리와 이진탐색트리(Binary Search Tree)

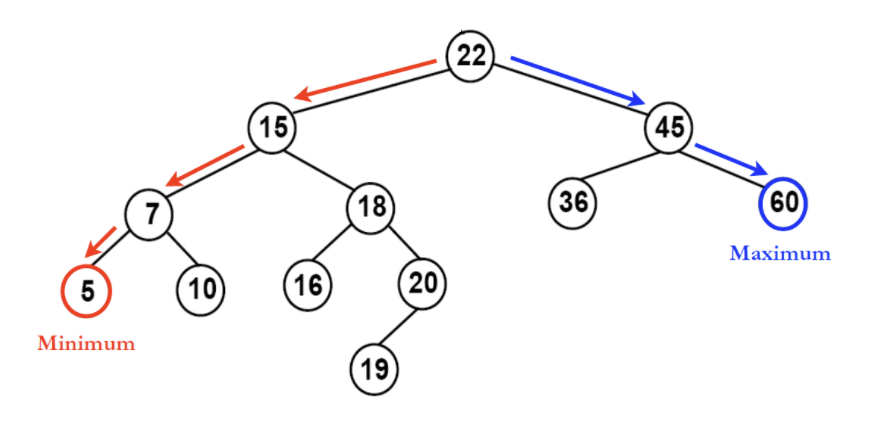
이진트리 (Binary Tree)

• 트리 중에서도 이진트리 형태로, 탐색(검색) 알고리즘 구현에 많이 사용되는 자료구조이다.
• 최대 Branch가 2개인 트리

이진탐색트리 (Binary Search Tree) 가 나오게 된 이유

이진탐색의 경우 탐색에 소요되는 계산복잡성은 𝑂(log𝑛)으로 빠르지만 자료 입력, 삭제가 불가능하다,반면 연결리스트의 경우 자료 입력, 삭제에 필요한 계산복잡성은 𝑂(1)로 효율적이지만 탐색하는 데에는 𝑂(𝑛)의 계산복잡성이 발생한다 이를 해결하기 위해 나온것이 바로 이진탐색트리

• 이진탐색트리란 이진탐색(binary search)과 연결리스트(linked list)를 결합한 자료구조의 일종
• 이진트리에 추가적인 조건이 있는 트리
• 위에있는 이미지와 같이 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있는 트리
• 빈번한 자료 입력과 삭제를 가능하게 함

이진탐색트리의 주 용도

• 데이터 검색(탐색)에 많이 사용
• 탐색 속도를 개선할때 사용

이진트리 vs 정렬된 배열탐색

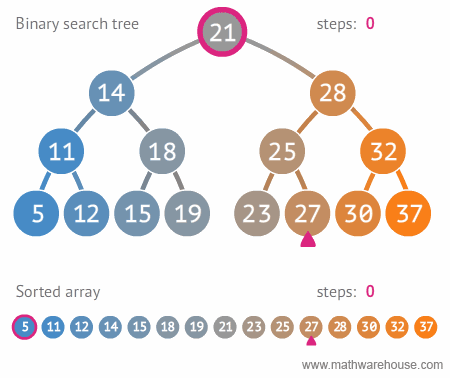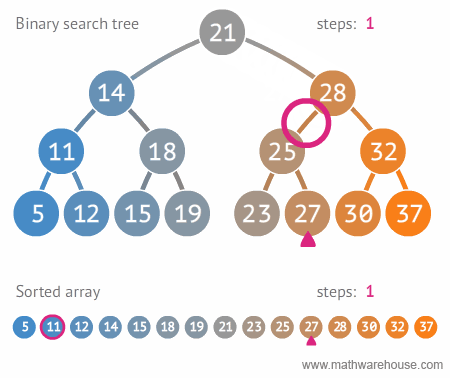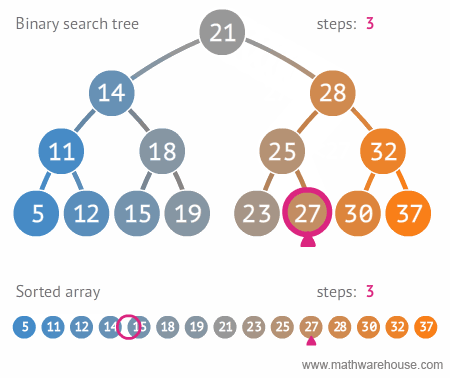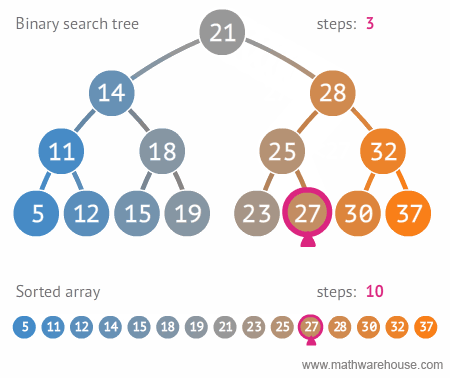
힙(Heap)

트리를 기반으로 변형된 형태의로 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.

데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
완전 이진 트리라는 말은 아니다

완전 이진 트리 : 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리

특정노드는 자식노드보다 크거나 최소한 같은 값을 갖는다.

힙을 사용하는 이유

• 배열에 데이터를 넣고, 최대값 최소값을 찾으려면 O(n)이 걸리지만 힙에 데이터를 넣고 최대값 최소값을 찾으려면 O(logn)이 걸림
• 우선순위 큐와 같이 최대값, 최소값을 빠르게 찾아야 하는 자료구조, 알고리즘에 활용될 수 있음
• 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않음)

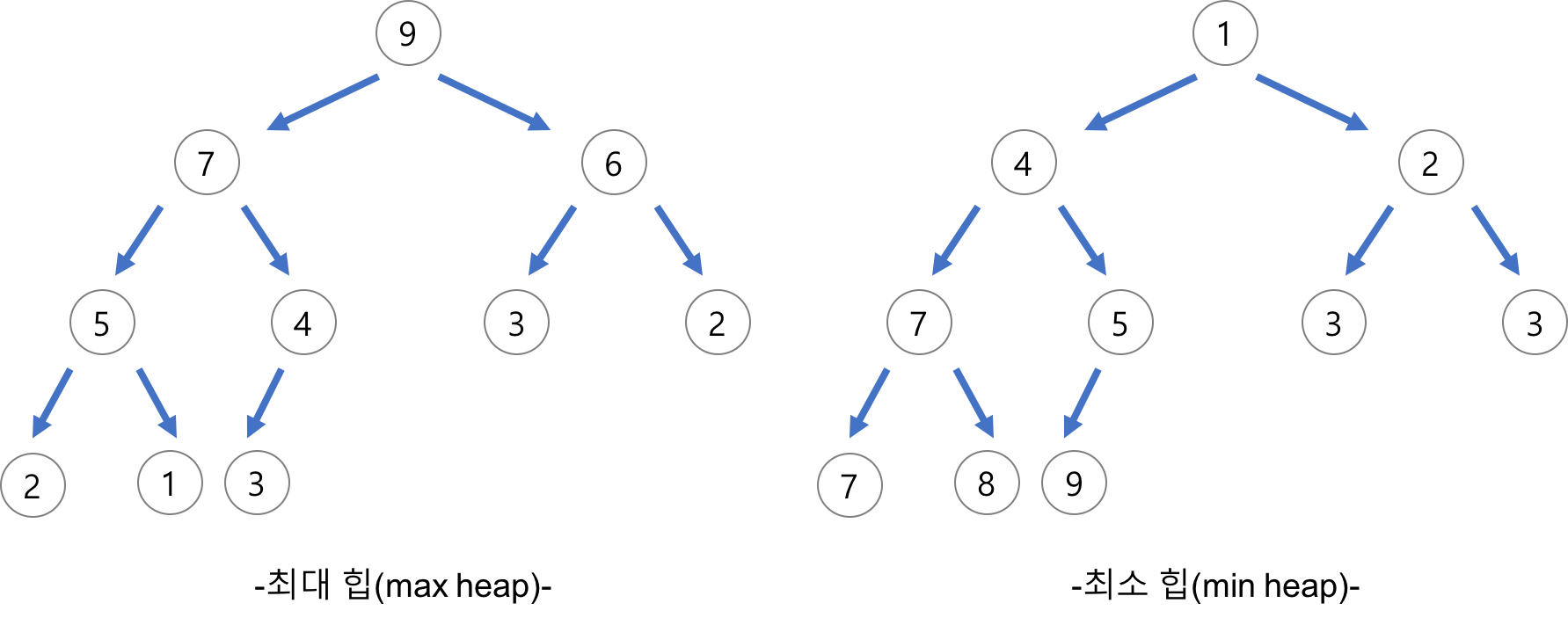
힙의 구조

• 힙은 최대값을 구하기 위한 구조(Max Heap), 최소값을 구하기 위한 구조(Min Heap)으로 분류할 수 있다.
• 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다.(최대힙)
  최소힙의 경우 그 반대
• 완전 이진 트리 형태를 갖는다.

힙 구현

일반적으로 힙 구현은 배열 자료구조를 활용한다.

Reference

https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/
https://blog.penjee.com/5-gifs-to-understand-binary-search-tree/
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
https://medium.com/quantum-ant/%ED%8A%B8%EB%A6%AC-tree-cec69cfddb14