[python] 백준 2342 : Dance Dance Revolution

문제 링크
https://www.acmicpc.net/problem/2342

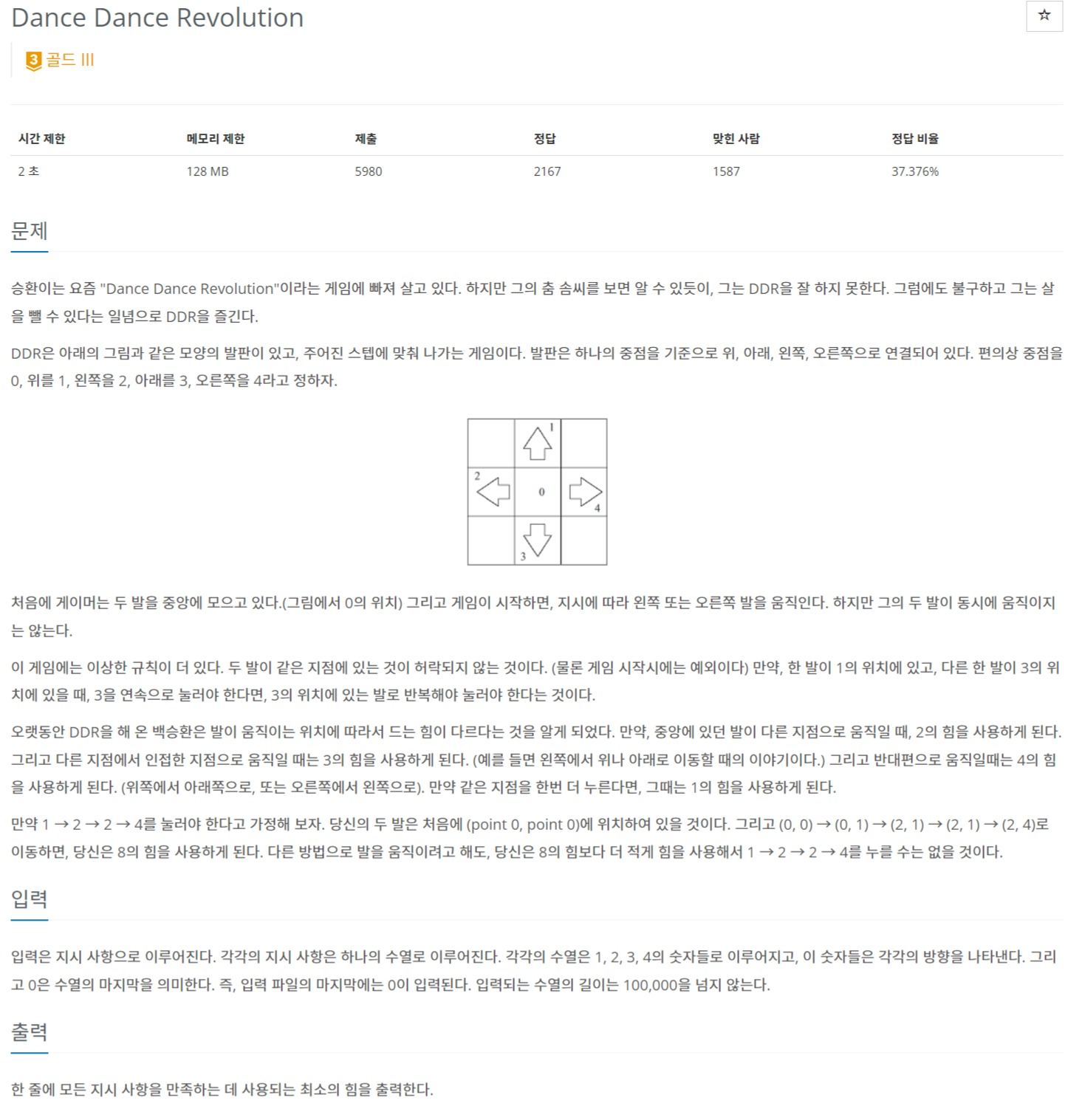
문제 조건

1. 같은 지점 한 번 더 누를 때: 비용 == 1
2. 중앙에서 다른 지점으로 움직일 때: 비용 == 2
3. 중앙이 아닌 곳에서 인접한 지점으로 (ex. 왼쪽 -> 위쪽 or 아래쪽) 움직일 때: 비용 3
4. 반대편으로(ex. 위쪽 -> 아래쪽) 움직일 때: 비용 == 4

• 단, 맨 처음 상황을 제외하고, 두 발이 같은 지점에 있을 수 없음

주어진 움직임을 최소 비용으로 구하라.

접근 1

완전 탐색을 할 수는 없었기(지수 시간 복잡도)에 그 다음에 든 생각은 그리디로 푸는 것이었다.

조건만 잘 따져준다면 풀릴 것 같았기 때문에 자신감을 가지고 그리디로 풀어보고자 하였다. 이때 한 생각으로는, 일단 무조건 가까운 발을 먼저 이동시키는 것이었다(비용이 적게 드는 움직임 먼저!).

고려한 예외 조건으로는 쫙 벌린 상태(1,3 또는 2,4에 발이 있는 상태)에서 그 사이에 있는 위치로 이동하는 경우이다. 예를 들어 지금 현재 발이 1,3 에 있다고 치고, 다음 위치가 2인 경우이다. 1번에 있는 발을 2로 옮기는 것과 3번에 있는 발을 2로 옮기는 것의 비용이 같기 때문에, 이후에 어떤 것이 나오냐에 따라 2번으로 옮길 발을 정하는 것이다.

말로 설명하니 어려운데
(1,3) 인 상황에서 다음 위치가 2라고 치자.
아래처럼 두가지 경우가 생기는데, 이 이후의 위치를 살피자는 것이다.

(1,3) -> (2,3)
(1,3) -> (1,2)

먼저 2 이후에 3이 나오는 경우, 즉 (1,3) -> 2 눌러야함 -> 3 눌러야함 이러한 경우에는 (1,3) -> (2,3) -> (2,3) 이 유리할 것이며,
반대로 2 이후에 1이 나오는 경우, 즉 (1,3) -> 2 눌러야함 -> 1 눌러야함 이러한 경우에는 (1,3) -> (1,2) -> (1,2) 가 유리할 것이다.

그리고 2 이후에 2가 또 나오는 경우에는 어차피 중복처리를 하면 되므로 다음 위치가 다른 위치(1,3,4)가 될때까지 순회한다.
마지막으로 2 이후에 4가 나오는 경우 어떤 선택을 해도 결과가 같으므로 (최종적으로 (1,3) 에서 (2,4)가 됨) 고려하지 않았다.

모든 예외를 처리했다고 생각했지만...
첫두번을 한쪽발로만 밟는 경우를 생각하지 못했다.
입력: 1 2 3 2 0
답: 8
내 결과: 10

그래서 dp를 이용하기로 마음먹었다...

접근 2

dp[i][l][r] = i번째 움직임을 (l,r)의 발 위치로 수행했을 때 드는 힘의 총 합 (이 때 l 또는 r 중 하나는 반드시 i번째 움직임을 포함).

점화식은 다음과 같다.

dp = [[[MAX + 1 for _ in range(5)] for _ in range(5)] for _ in range(n + 1)]
dp[-1][0][0] = 0

for i in range(n):
    # l = move[i], 왼발로 이번 위치 누를 때, 즉 이번에 왼발이 움직일 것
    for r in range(5):  # 왼발이 움직이니 오른발은 고정
        for k in range(5):  # k 는 왼발의 이전 위치.
            add = get_add(move[i], k)  # 왼발이 k에서 move[i]로 움직일 때 드는 비용
            dp[i][move[i]][r] = min(dp[i][move[i]][r], dp[i - 1][k][r] + add)

    # r = move[i], 오른발로 이번 위치 누를 때, 즉 이번에 오른발이 움직일 것
    for l in range(5):  # 오른발이 움직이니 왼발은 고정
        for k in range(5):  # k는 오른발의 이전 위치.
            add = get_add(move[i], k)  # 오른발이 k에서 move[i]로 움직일 때 드는 비용
            dp[i][l][move[i]] = min(dp[i][l][move[i]], dp[i - 1][l][k] + add)

조금 복잡해보이는데...
왼발을 이동하는 것만 생각해보자면, 어쨋든 i번째 움직임에서 왼발은 move[i]의 위치로 이동해야 한다.
그러면 오른발은 움직이지 않았다는 얘기이므로, 임의의 오른발 위치에 대해 왼발의 이전 위치 k 의 값을 변화시켜주면서 값을 갱신하면 된다는 것이다. 임의의 오른발 위치 또한 0,1,2,3,4 다섯가지 경우 모두 생각해주면 된다.

최대 100000 * 5 * 5 * 2 = 500만 번 정도 연산하므로 충분히 시간 내에 돌릴 수 있다고 판단했다.

정답 코드

import sys

sys.setrecursionlimit(10 ** 8)
input = lambda: sys.stdin.readline().rstrip()

MAX = 400000


def get_add(lr, k): # 어떤 발이 k->lr 발로 갈 때 드는 비용
    if k == 0:
        if lr == 0:
            return 0
        else:
            return 2
    elif k == lr:
        return 1
    elif abs(k - lr) == 1 or abs(k - lr) == 3:
        return 3
    else:
        return 4


move = list(map(int, input().split()))
move.pop()
n = len(move)
if n == 0:
    print(0)
    exit()

dp = [[[MAX + 1 for _ in range(5)] for _ in range(5)] for _ in range(n + 1)]
dp[-1][0][0] = 0

for i in range(n):
    # l = move[i], 왼발로 이번 위치 누를 때, 즉 이번에 왼발이 움직일 것
    for r in range(5):  # 왼발이 움직이니 오른발은 고정
        for k in range(5):  # k 는 왼발의 이전 위치.
            add = get_add(move[i], k)  # 왼발이 k에서 move[i]로 움직일 때 드는 비용
            dp[i][move[i]][r] = min(dp[i][move[i]][r], dp[i - 1][k][r] + add)

    # r = move[i], 오른발로 이번 위치 누를 때, 즉 이번에 오른발이 움직일 것
    for l in range(5):  # 오른발이 움직이니 왼발은 고정
        for k in range(5):  # k는 오른발의 이전 위치.
            add = get_add(move[i], k)  # 오른발이 k에서 move[i]로 움직일 때 드는 비용
            dp[i][l][move[i]] = min(dp[i][l][move[i]], dp[i - 1][l][k] + add)

m = MAX + 1
for l in range(5):
    for r in range(5):
        m = min(m, dp[n - 1][l][r])
print(m)