[R] Queueing System

A Single Server Queueing System

서비스 스테이션에서 고객이 Nonhomogeneous Poisson Process에 따라 대기열에 도착하고,
강도 함수 $\lambda(t)$를 따른다고 가정하자.

지금 우리가 제공할 수 있는 서버는 1개이다. 고객이 도착했을 때 시스템 내에 아무도 없으면 고객이 서비스를 받게 되고, 시스템 내 서비스를 받고 있는 고객이 있으면 대기열에 들어간다.

서버가 고객을 처리하고 나면 대기열에서 가장 오래 기다린 고객부터 처리한다. >> (Queue)
만약 대기 중인 고객이 없으면 그대로 서버는 비어있게 되는 것이다. 이 시스템을 시뮬레이션으로 구현해보자.

• Time variable
  $t$ : 현재 시각
• Counter variable
  $N_A$ : $t$까지 도착한 고객의 수
  $N_D$ : $t$까지 서비스 완료된 고객의 수
• System State Variable
  $n$ : 시각 $t$에 시스템 안에 있는 고객의 수 (현재 서비스 중인 고객 1명 + 대기 고객 수. 0일 수 있음.)
• Event List
  $t_A$ : 현재 시각 $t$ 이후에 다음 고객이 도착하는 시각. $t_A>T$인 고객은 마감 시각 이후에 도착했으므로 시스템에 들어오지 못함. 즉 $n$을 증가시키지 않음.
  $t_D$ : 현재 시각 $t$에 서비스 받고 있는 고객의 서비스 완료 시각. 현재 서비스 중인 고객이 없으면 $t_D=\infin$ 로 초기화

• Output Variable
  $A(i)$ : $i$번째 고객의 도착시각
  $D(i)$ : $i$번째 고객의 서비스 완료 시각
  $T_p$ : 직원의 초과근무 시간 (마지막 고객의 서비스 완료시각이 $T$를 넘을 경우 서비스 완료시각에서 $T$를 뺀 시간)
  

Simulation Logic

Initialize

$t=t_A=t_D=0,\ n=0$
첫 고객의 도착시간을 $T_0$라고 할 때, $\ t_A=T_0, \ t_D=\infin$

Event List인 $t_A$와 $t_D$ 값에 따라 갱신하고 저장해야 할 정보가 달라진다.

Case 1 : $t_A\leq t_D$ 이고 $t_A\leq T$

기존 고객의 서비스가 끝나기 전에 새 고객이 먼저 도착했으며 도착시각은 마감 전이다.

• 현재 시각을 $t_A$로 갱신.
• 고객이 추가로 도착했으므로 $N_A=N_A+1.$
• 시스템 내 고객 수 $n = n + 1$
• 만약 $n=1$이면 시스템이 빈 것이므로 새로 온 고객의 서비스 소요 시간($Y$)을 생성하여 $t_D=t+Y$로 설정. $N_A$번째 고객의 도착시간 저장 $A[N_A] = t$

Case 2 : $t_A< t_D$ 이고 $t_D\leq T$

새 고객이 도착하기 전에 한 고객에 대한 서비스가 끝났으며 끝난 시각이 마감 전이다. 대기 중인 고객이 있다면 다음 고객에 대한 서비스를 바로 시작한다. 대기 중인 고객이 없다면 $t_D=\infin$로 초기화한다.

• 현재시각을 $t_D$로 설정.
• 시스템 내 고객 수 $n$을 $n-1$로 감소.
• 서비스 완료 고객 수($N_D$)를 $N_D+1$로 증가.
• 만약 $n=0$이면 시스템 내 고객이 없기에 $t_D=\infin$로 설정하고, 그렇지 않으면 다음 서비스 시간($t_D=t+Y$) 생성
• $N_D$번째 서비스 완료시간 저장 $D[N_D]=t$

Case 3 : $min(t_A,t_D)>T$ 이고 $n>0$

마감 시간이 지났지만 서비스해야 할 고객이 아직 있다.

• 현재 시각을 $t_D$로 설정 (마감 후에는 신규 고객이 없음.)
• 시스템 내 고객 수 $n$을 $n-1$로 감소.
• 서비스 완료 고객 수($N_D$)를 $N_D+1$로 증가.
• 만약 $n>0$이면 다음 서비스 시간$(t_D=t+Y)$ 생성
• $N_D$번째 서비스 완료시간 저장 $D[N_D]=t$

Case 4 : $min(t_A,t_D)>T$ 이고 $n=0$

마감 시간이 지났고 시스템에 고객이 없으므로 시뮬레이션을 종료한다.

• 마지막 고객이 떠난 이후 소요된 시간을 기록한다. (초과근무 계산을 위해)

위 절차를 순서도로 표현하면 다음과 같다.

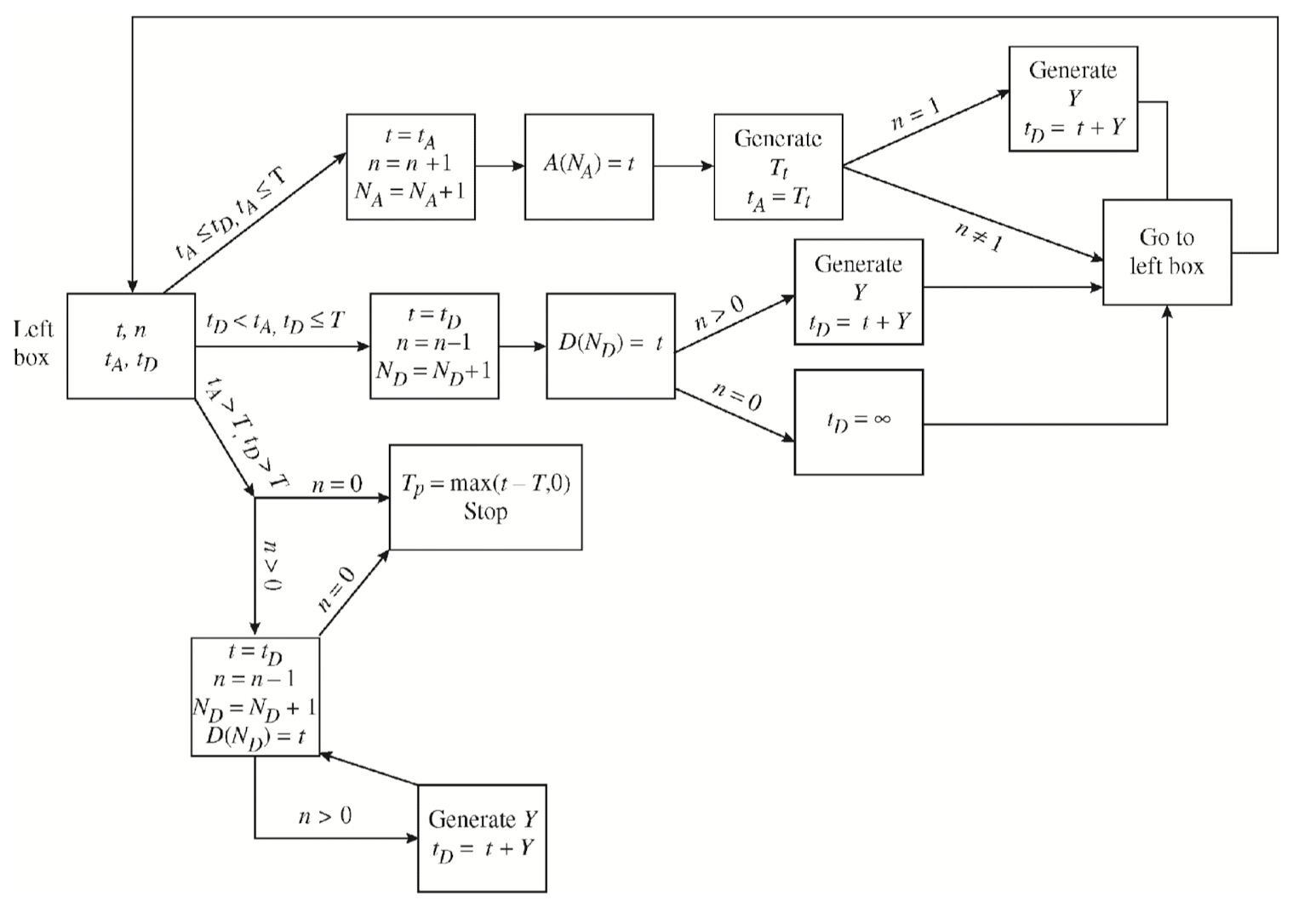
이 로직을 적용할 수 있는 예제를 풀어보자.

Single Server Queueing System에서 고객이 시스템 내에서 보내는 평균 체류시간과
직원의 평균 초과 근무시간을 추정하라. 여기서 고객 도착 간격은 Rate이 10인 지수 분포, 서비스 완료시간 간격은 shape이 3, Scale이 1/40인 감마분포를 따른다. 그리고 마감시간은 $T=9$이다.

위 시뮬레이션을 100번 실행하는 코드를 구현해보자.

> n.sim = 100
> rate = 10
> shape = 3; scale = 1/40
> T = 9
> time.over = time.spend = numeric(n.sim) # 고객들의 평균체류시간과 직원(server)의 초과근무시간
> for (i in (1:n.sim)) {
+   t = NofA = NofD = 0
+   n = 0
+   tA = rexp(1,rate)
+   tD = Inf
+   A = D = numeric()
+   repeat {
+     if (tA <= tD & tA <= T){
+       t = tA; NofA = NofA + 1; n = n + 1
+       tA = t + rexp(1,rate)
+       if (n == 1) tD = t + rgamma(n=1,shape,scale=scale)
+       A[NofA] = t
+     }
+     if (tD < tA & tD <= T){
+       t = tD; n = n - 1; NofD = NofD + 1
+       if (n == 0) tD = Inf else tD = t + rgamma(n=1,shape,scale=scale)
+       D[NofD] = t
+     }
+     if (min(tA,tD) > T & n > 0){
+       t = tD; n = n - 1; NofD = NofD + 1
+       if (n > 0) tD = t + rgamma(n=1,shape,scale=scale)
+       D[NofD] = t
+     }
+     if (min(tA,tD) > T & n == 0) break
+   }
+   time.spend[i] = mean(D-A); time.over[i] = max(t-T,0); 
+ }
> cat("고객 한 명이 시스템에 체류하는 시간의 평균 =",mean(time.spend),"\n직원의 초과근무시간의 평균 =",mean(time.over))
고객 한 명이 시스템에 체류하는 시간의 평균 = 0.2048746 
직원의 초과근무시간의 평균 = 0.1358676

time.over와 time.spend에 시뮬레이션에서 출력된 고객 평균 체류시간과 직원의 초과근무시간을 저장했다.
최종적으로 두 벡터에 저장된 값들의 평균을 출력하는 식으로 마무리했다.

그럼 서버의 휴식시간(Idle time)의 총합은 어떻게 계산할 수 있을까?

> n.sim = 100
> rate = 10
> shape = 3; scale = 1/40
> T = 9
> time.idle = numeric(n.sim)
> for (i in (1:n.sim)) {
+   t = NofA = NofD = 0
+   n = 0
+   tA = rexp(1,rate)
+   tD = Inf
+   A = D = numeric()
+   repeat {
+     if (tA <= tD & tA <= T){
+       t = tA; NofA = NofA + 1; n = n + 1
+       tA = t + rexp(1,rate)
+       if (n == 1) tD = t + rgamma(n=1,shape,scale=scale)
+       A[NofA] = t
+     }
+     if (tD < tA & tD <= T){
+       t = tD; n = n - 1; NofD = NofD + 1
+       if (n == 0) tD = Inf else tD = t + rgamma(n=1,shape,scale=scale)
+       D[NofD] = t
+     }
+     if (min(tA,tD) > T & n > 0){
+       t = tD; n = n - 1; NofD = NofD + 1
+       if (n > 0) tD = t + rgamma(n=1,shape,scale=scale)
+       D[NofD] = t
+     }
+     if (min(tA,tD) > T & n == 0) break
+   }
+   gap = c(A, T) - c(0, D)
+   #time.idle[i] = sum(gap[gap > 0])
+   time.idle[i] = sum(pmax(gap, 0))
+ }
> cat(mean(time.idle), "+/-", 2*sd(time.idle)/sqrt(n.sim),"\n")
2.36555 +/- 0.1479931 

고객들의 도착시간과 서비스 완료시간을 이미 알고 있다는 점을 생각해 기존 코드를 조금 수정했다.

우선 (도착시간 - 서비스 완료시간)을 계산하기 위해 D의 가장 첫 인덱스에 0을 추가했다.
이 값이 양수라면 $k$번째 고객의 서비스 완료 시간에 비해 $k+1$번째 고객의 도착시간이 늦다는 의미로, 그만큼의 공백이 발생했다는 것이다.

따라서 그 시간들의 합을 구하면 서버 휴식시간의 총합을 얻을 수 있다.