10주차-ADAS(1)

detection, tracking

객체 디텍션만하면 다음 프레임에서 객체의 위치가 바뀌어도 같은 객체인지 인식하지 못함
따라서 객체 트래킹이 필요

image processing / computer vision 차이

이미지 프로세싱: 이미지 input - 이미지 output
컴퓨터 비전: 이미지 input - 디지털 데이터 output

자율주행 현실적인 문제들

lane detection 문제들
1. 도로 위 가드레일 그림자가 져서 차선으로 오해해 검출될 수도 - HSV 모델로 그림자 필터링 가능
2. 카메라에 들어오는 정보 다 받아들이면 컴퓨테이팅 파워가 넘 많이 듬 - roi 선정으로 버드아이-뷰(탑뷰)를 만들어서 필요한 데이터 선별
3. 곡선 도로 주행에서, 직선 앞의 휘는 가드레일을 철판으로 인식해서 속도를 못내거나, 철판 맨홀뚜껑 보고 스탑할 수도 있음 - 차선 디텍션으로 곡률값을 알고 곡률 내에 있는 철판만 인식하도록 함
4. 허프라인으로는 곡선 검출 불가 - 실무에서는 바이너리 이미지로 버드아이 뷰를 만들고 3d line fitting을 함

센서의 한계
카메라, 레이더, 라이다 센서는 각각의 장단점을 가지고 있음, 각각의 장점을 이용해 센서퓨전을 해서 가장 정확한 정보를 인지해야함

관련 법 제정 한계
사고났을 때 책임문제

센서 퓨전의 장점

데이터 판별 범위가 늘어남(카메라로 객체 RGB 데이터, 라이다로 객체 인식 및 거리, 인식 범위
센서퓨전하면 데이터 범위가 혼합되어서 객체가 붙어있을 때, 또는 차량이 가드레일 근처에 가까이 있을 때, 모호성이 생김 - 불필요한 고려, 계산을 줄이기 위해 객체에 범위를 설정하는 gating 작업이 필요함

Sensor Circle

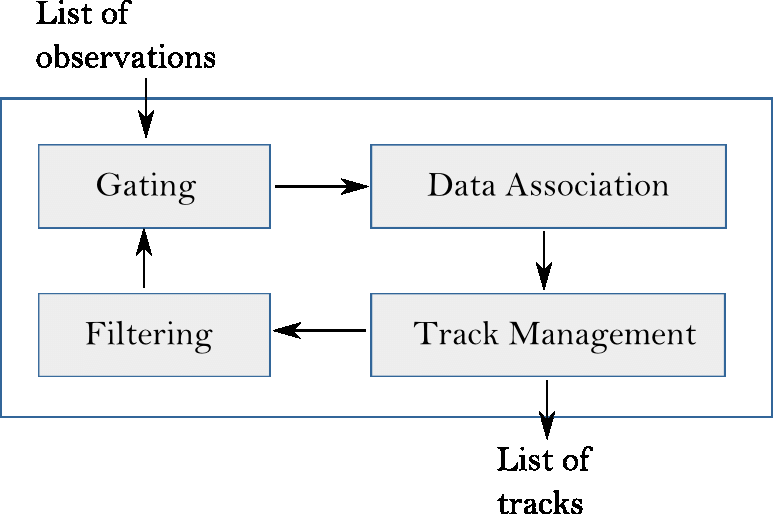
filtering엔 칼만필터...

---

베이지안 이론

어떤 사건의 확률을 구할 때 두가지 방법론이 있음 - 빈도론, 베이지안 이론
베이지안 이론은 반복적으로 시행가능한 빈도론과 다르게 일어나지 않은 일에 대한 확률을 구하는 방법
베이지안 이론에 따르면, 가능도(likelihood)와 사전확률(prior belief), 증거확률(evidence)을 알면 사후확률(posterior)을 구할 수 있음

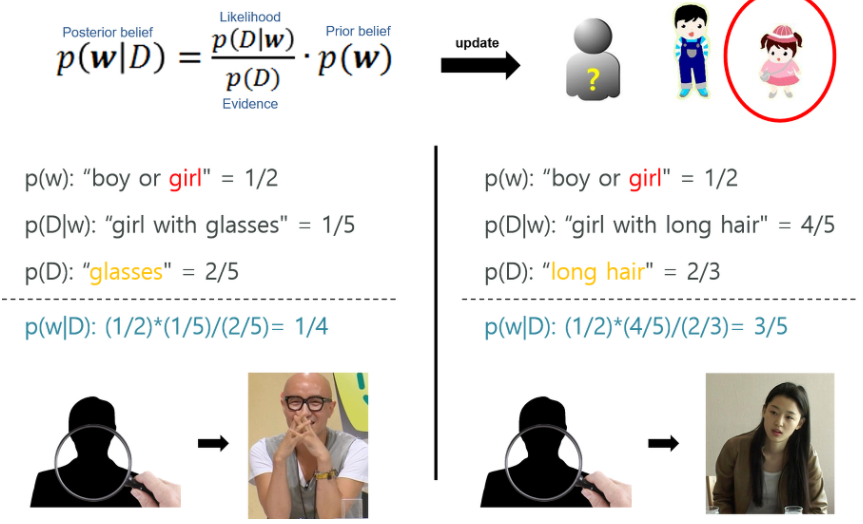
예를 들면, 형체를 파악하지 못한 인물 형상 데이터에 대해,
여성일 확률 1/2 (prior)
머리가 길고 여성일 확률 4/5 (likelihood)
머리가 길 확률 2/3 (evidence)
머리가 긴 사람이 여성일 확률(posterior)
= prior x (likelihood/evidence) = 0.5 x (0.8 / 0.66) = 0.6

베이지안 확률은 머신러닝 이해에 굉장히 중요!
머신 러닝은 데이터셋이 주어졌을 때, 특정 사건 혹은 가설의 확률을 높여줄 수 있는 최적의 모델을 찾는 것을 목적으로 한다. 따라서 베이지안 모델이 주어진 정보를 업데이트 해나가면서, 최적의 사후확률을 계산하는 방식과 일맥상통한다.

마코프 체인

마코프 체인 이론에 의하면 한 상태(state)의 확률은 단지 그 이전 상태에만 의존. 즉 한 상태에서 다른 상태로의 전이(transition)는 그동안 상태 전이에 대한 긴 이력(history)을 필요로 하지 않고 바로 직전 상태에서의 전이로 추정 가능.

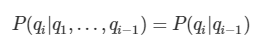
로봇의 동작을 예로 들면, 100번째 상태의 위치를 예측하기 위해서 1번째부터 99번째까지를 고려할 필요없이 99번째 상태만 고려하면 된다는 것 - computation power 대폭 절약

베이즈 필터

1. 베이즈 필터 정의 : 확률 기반의 recursive 한 filter
   베이지안 이론을 이용하면 prior, likelihood을 가지고 posterior를 구할 수 있음, 구한 posterior을 다음 스텝에 prior로 넣어서 recursive함

2. 베이즈 필터 목적 :
   

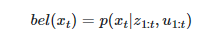
xt는 t시점의 상태값, zt는 센서 입력값, ut는 제어 입력값
위 수식 해석하면 알고리즘의 시작부터 현재 시점 t까지의 센서 입력값과 제어 입력값을 이용하여 현재 상태를 확률적으로 추정하는 것, 즉 베이즈 필터는 센서값, 제어값을 이용하여 현재 상태를 추정하는 알고리즘이고 칼만 필터 등에 적용 가능

3. 베이즈 필터 역할
   1) motion model을 통한 예측, 제어값 이용 - 이전 상태값과 물리 수식(거=속x시)을 통해 현재 위치 예측
   2) observation model을 통한 예측, 센서값 이용 - GPS와 같은 센서 장치로 현재 위치 예측

• 베이즈 필터는 위 값 중 하나만을 사용하는 것이 아니라 두 가지 값을 모두 사용하여 하나의 값으로 퓨전하여 사용, 예를 들면 모션 모델로 위치값을 먼저 구하고 그 위치에 센서값을 통해 보완함, 하나만 사용하는 것 보다 더 정확한 위치 예측 가능

4. 베이즈 필터 로봇 예시

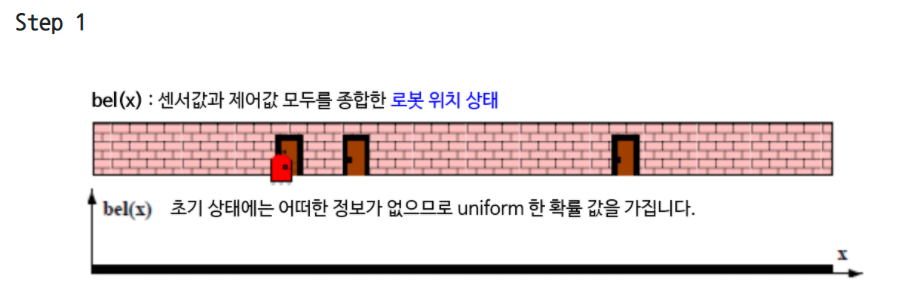
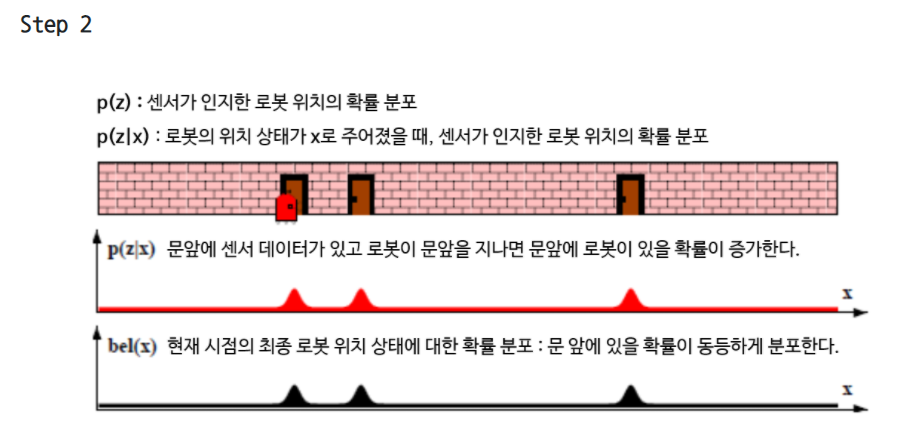
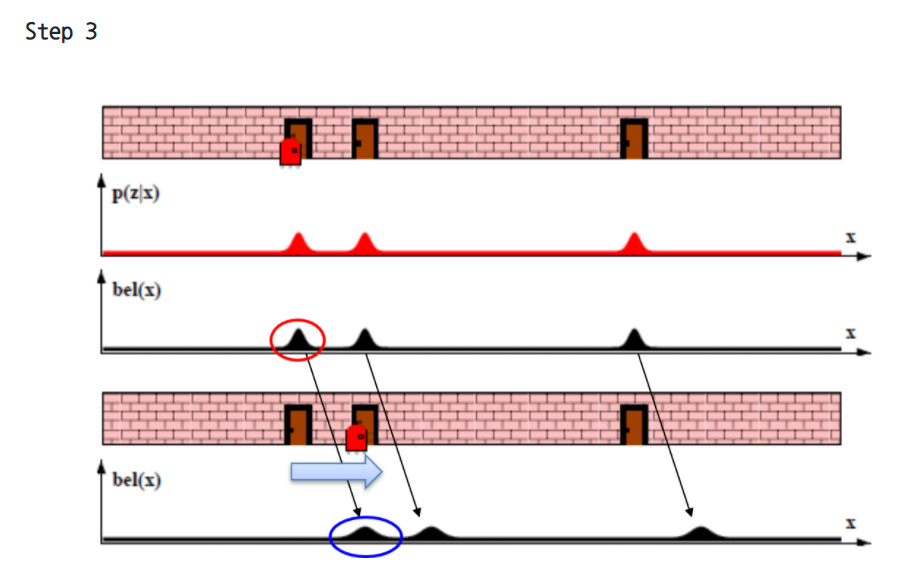
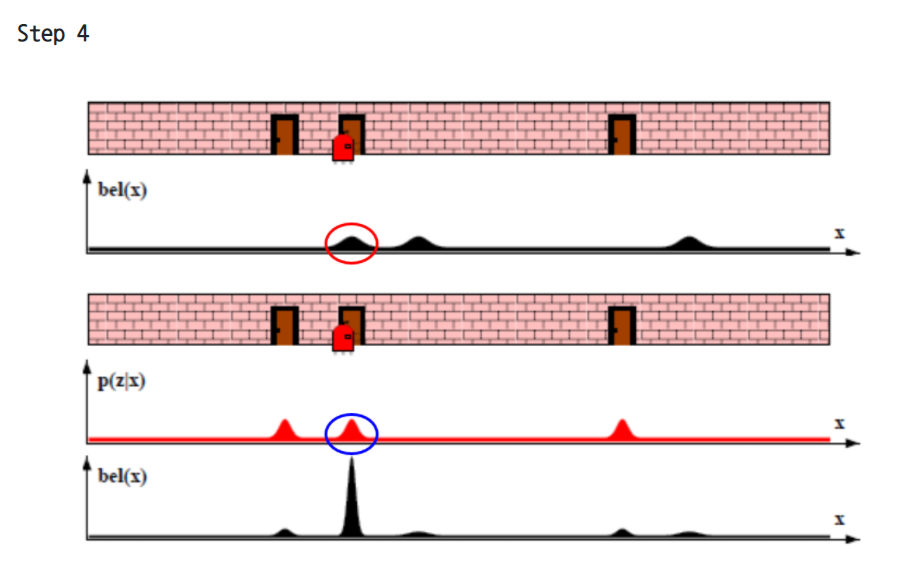
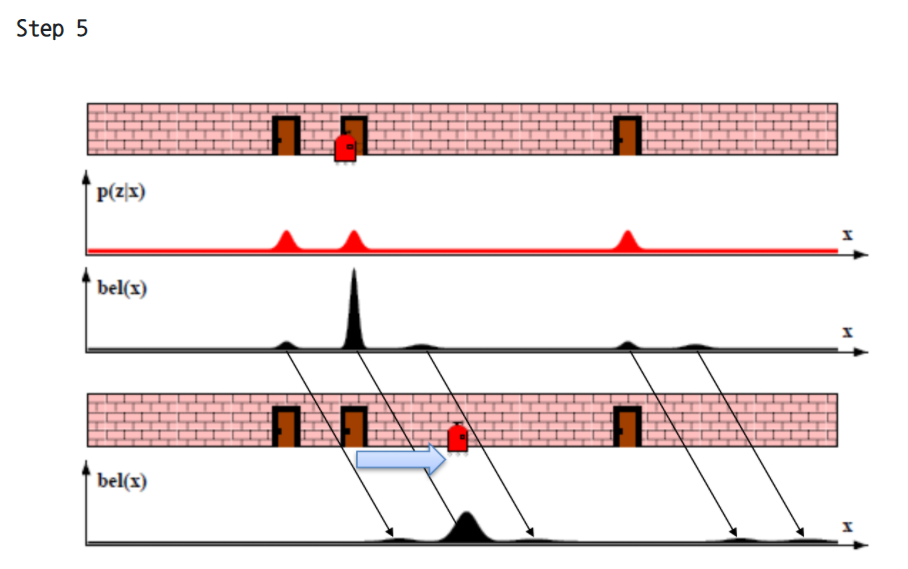
자세한 설명 아래 출처에, 그림 그리면서 설명 가능하게!

베이지안 이론 출처 : https://bioinformaticsandme.tistory.com/47

베이즈 필터 출처 : https://gaussian37.github.io/autodrive-ose-bayes_filter/