10주차-ADAS(2)

칼만 필터

1. 칼만 필터 정의: x_t를 우리가 관심을 가지는 시스템의 상태 벡터(위치, 속도로 이루어짐)라고 할 때, 가장 높은 확률의 추정값 x_t(hat)을 찾아내는 알고리즘

ex) 로봇을 예로 들면, 로봇의 센서를 통해 얻은 자신의 상태벡터 측정값 z_k를 칼만 필터에 입력하면 가장 높은 확률의 상태벡터 추정값 x_k를 출력한다.

// 2. 칼만 필터 목적: 알고싶은 변수를 직접적으로 확인할 수 없고 간접적인 방법으로 유도해서 알아내야 할 때, 센서 퓨전으로 값을 측정했는데 노이즈가 발생할 때 노이즈 문제를 개선하기 위해

3. 칼만 필터 동작방법

칼만필터 사용하기 전 가정
1. 상태값을 예측할 때 위치, 속도와 같은 랜덤한 변수는 가우시안 분포를 띈다고 가정한다.
2. 상태방정식은 선형적이다.

우선, 칼만필터는 1. 상태값 예측, 2. 측정값 업데이트 두 단계로 동작함

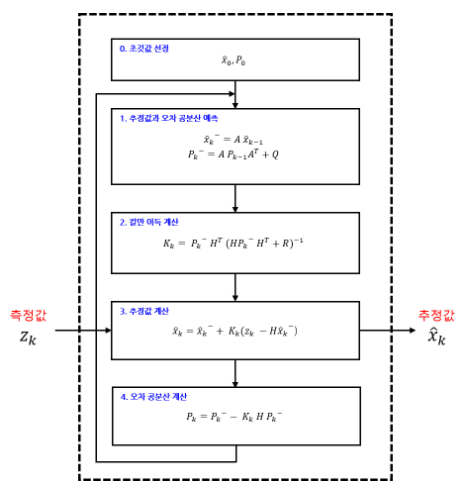
1. 상태값 예측
   첫번째 단계인 예측 과정에서는 이전 단계에서 계산한 추정값()을 사용하여 시스템 모델()과의 계산을 통해 새로운 추정값을 예측합니다.
   이때, 예측한 값이 평균을 기준으로 어느 정도로 분포되어 있는지 이전 오차 공분산()을 사용하여 새로운 오차 공분산()도 함께 예측하게 됩니다.
   예측 과정이 끝나게 되면, 칼만 이득을 계산하게 됩니다.
   칼만 이득을 계산할 때는 예측 과정에서 계산한 오차 공분산의 예측값()과 측정값의 노이즈()를 사용합니다.

중간. 칼만 이득 계산

2. 측정값 업데이트
   추정 과정에서는 추정값과 오차 공분산을 최종적으로 계산하게 됩니다.
   추정 과정에서 추정값을 계산할 때는 예측 과정에서 계산했던 (추정값의 예측값)과 입력으로 받은 (측정값)을 이용합니다.
   추정값의 계산식은 예측 과정에서 구한 에 와 의 차이를 보상하여(더하여) 계산하게 됩니다.
   이때, 칼만 이득이 사용되는데 바로 와 의 차이()의 결과에 영향을 미칩니다.
   칼만 이득은 와 같은 추정값의 계산식에서 값을 조절하여 에 더해주게 됩니다.

칼만필터 모델링을 위해 중요한 인자 -> A, H, Q, R
A: 상태방정식에 들어있는 상태전이 행렬
H: 가우시안 분포 합성할 때 위치도메인, 시간도메인 등 다른 도메인을 통일시켜주는 스케일링 인자
Q: 오차공분산 P_k 식에 들어있는 프로세스 노이즈의 분산, Q가 높으면 오차공분산도 높아져서 분포의 오차가 커짐
R: 칼만 이득 K 식에 들어있는 센서 노이즈, R이 높으면 K가 작아져서 센서 측정값 Z_k의 비중이 작아지고, 위치 예측값 X_k의 비중이 커진다. 반대로 R이 작으면 K가 높아지고 그에 따라 측정값, 예측값 비중이 달라진다.

버드아이 뷰 코드 분석

import numpy as np
import math
import cv2


### Camera coordinate to vehicle coordinate(ISO)
def RotX(Pitch):
      Pitch = np.deg2rad(Pitch)
      return [[1, 0, 0], [0, math.cos(Pitch), -math.sin(Pitch)], [0, math.sin(Pitch), math.cos(Pitch)]]

def RotY(Yaw):
      Yaw = np.deg2rad(Yaw)
      return [[math.cos(Yaw), 0, math.sin(Yaw)], [0, 1, 0], [-math.sin(Yaw), 0, math.cos(Yaw)]]

def RotZ(Roll):
      Roll = np.deg2rad(Roll)
      return [[math.cos(Roll), -math.sin(Roll), 0], [math.sin(Roll), math.cos(Roll), 0], [0, 0, 1]]      

### Camera parameter setting
ImageSize = (480, 640)
FocalLength = (309.4362, 344.2161)
PrinciplePoint = (318.9034, 257.5352)
IntrinsicMatrix = ((FocalLength[0], 0, 0), (0, FocalLength[1], 0), (PrinciplePoint[0], PrinciplePoint[1], 1))
Height = 2.1798
Pitch = 14
Yaw = 0
Roll = 0

### Bird's eye view setting
DistAhead = 30
SpaceToOneSide = 6
BottomOffset = 3.0

OutView = (BottomOffset, DistAhead, -SpaceToOneSide, SpaceToOneSide)
OutImageSize = [math.nan, 250]

WorldHW = (abs(OutView[1]-OutView[0]), abs(OutView[3]-OutView[2]))

Scale = (OutImageSize[1]-1)/WorldHW[1]
ScaleXY = (Scale, Scale)

OutDimFrac = Scale*WorldHW[0]
OutDim = round(OutDimFrac)+1
OutImageSize[0] = OutDim

### Homography Matrix Compute

#Translation Vector
Rotation = np.matmul(np.matmul(RotZ(-Yaw),RotX(90-Pitch)),RotZ(Roll))
TranslationinWorldUnits = (0, 0, Height)
Translation = [np.matmul(TranslationinWorldUnits, Rotation)]

#Rotation Matrix
RotationMatrix = np.matmul(RotY(180), np.matmul(RotZ(-90), np.matmul(RotZ(-Yaw), np.matmul(RotX(90-Pitch), RotZ(Roll)))))

#Camera Matrix
CameraMatrix = np.matmul(np.r_[RotationMatrix, Translation], IntrinsicMatrix)
CameraMatrix2D = np.r_[[CameraMatrix[0]], [CameraMatrix[1]], [CameraMatrix[3]]]

#Compute Vehicle-to-Image Projective Transform
VehicleHomo = np.linalg.inv(CameraMatrix2D)

AdjTransform = ((0, -1, 0), (-1, 0, 0), (0, 0, 1))
BevTransform = np.matmul(VehicleHomo, AdjTransform)

DyDxVehicle = (OutView[3], OutView[1])
tXY = [a*b for a,b in zip(ScaleXY, DyDxVehicle)]

#test = np.array([[1.,0.,0.],[0.,1.,0.],[0.,0.,1.]])
ViewMatrix = ((ScaleXY[0], 0, 0), (0, ScaleXY[1], 0), (tXY[0]+1, tXY[1]+1, 1))

T_Bev = np.matmul(BevTransform, ViewMatrix)
T_Bev = np.transpose(T_Bev)



### Main
src = cv2.imread("testImage.png", cv2.IMREAD_COLOR)

BirdEyeView = cv2.warpPerspective(src, T_Bev, (OutImageSize[1], OutImageSize[0]))

'''cv2.imshow("BEV", BirdEyeView)
cv2.waitKey(0)
cv2.destroyAllWindows()'''
 

### Distance

#Vehicle to Image
'''toOriginalImage = np.linalg.inv(np.transpose(T_Bev))
Trans = np.linalg.inv(np.matmul(toOriginalImage, VehicleHomo))
VehiclePoint = [[20, 0]]
XV = np.r_[VehiclePoint[0], np.shape(VehiclePoint)[0]]
UV = np.matmul(XV, Trans)

UV[0:2] = UV[0:2]/UV[2]
ImagePoints = list(map(int, UV[0:2]))

print(ImagePoints)
annotatedBEV1 = cv2.drawMarker(BirdEyeView, ImagePoints, (0,0,255))
cv2.putText(annotatedBEV1, "20 meters", ImagePoints, cv2.FONT_HERSHEY_DUPLEX, 0.5, (0,255,0))

cv2.imshow("BEV", annotatedBEV1)
cv2.waitKey(0)
cv2.destroyAllWindows()'''

#Image to Vehicle
toOriginalImage = np.linalg.inv(np.transpose(T_Bev))
Trans = np.matmul(toOriginalImage, VehicleHomo)
ImagePoint = [[120, 400]]

UI = ImagePoint
UI = np.r_[ImagePoint[0], np.shape(ImagePoint)[0]]
XI = np.matmul(UI, Trans)

XI[0:2] = XI[0:2]/XI[2]
XAhead = XI[0]

annotatedBEV2 = cv2.drawMarker(BirdEyeView, ImagePoint[0], (0,0,255))
cv2.putText(annotatedBEV2, str(round(XAhead, 2))+" meters", ImagePoint[0], cv2.FONT_HERSHEY_DUPLEX, 0.5, (0,255,0))

cv2.imshow("BEV", annotatedBEV2)
cv2.waitKey(0)
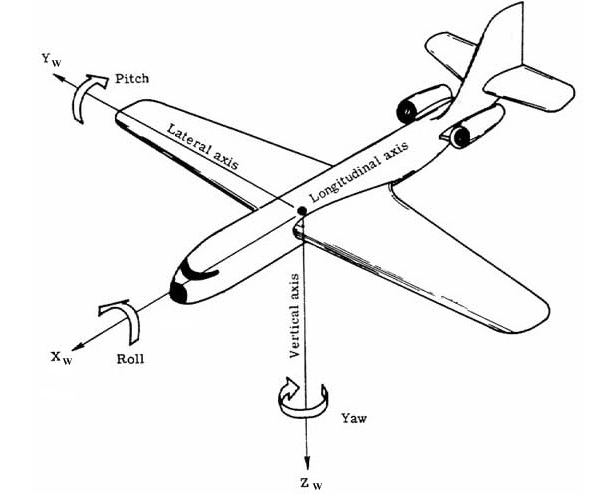
cv2.destroyAllWindows()

물체가 이동할 때, x,y,z축 기준 회전에 따라 오차 발생
x축 기준 회전오차 - 갸우뚱갸우뚱 roll
y축 기준 회전오차 - 끄덕끄덕 pitch
z축 기준 회전오차 - 도리도리 yaw

x축이 포함된 면에서 회전값은 pitch, y축이 포함된 면에서 회전값은 yaw, z축이 포함된 면에서 회전값은 roll이기 때문에, 코드에서 RotX(), RotY(), RotZ() 함수에 들어가는 인자가 각각 pitch, yaw, roll임
이 함수들은 카메라 좌표계에서 차량 좌표계로 이동하기 위해 사용될 것임

좌표계 이동?
동차좌표계 : 차원의 좌표를 1차원 증가시켜 표현하는 방법
(카메라좌표계 2차원 -> 차량좌표계 3차원)
반대로 차원을 낮춰서 표현하는건 투영 변환이라고 함

코드에서,
1. testImage.png가 2차원 행렬로 src에 저장
2. warpPerspective(image, matrix, (width, height))