딥러닝 과정
- 데이터 종류 파악 (데이터 종류에 따른 모델 설정 위해서)
- 가설 수립 (regression model - hx 설정)
- 비용함수 계산 (cost function - cost 설정)
- 경사하강법 (optimizer - opt 설정)
1. 데이터 종류 파악
통계학에서 자료는 구성하는 값의 특성에 따라 4종류로 나눌 수 있다.
- 명목 척도(nominal scale) : 속성을 분류하는 척도
- 순위 척도(ordinal scale) : 순서 관계를 밝혀주는 척도
- 간격 척도(interval scale) : 순서 사이의 간격이 균등한 척도
- 비율 척도(ratio scale) : 순서 사이의 간격이 균등하고, 절대값(0)이 존재하는 척도
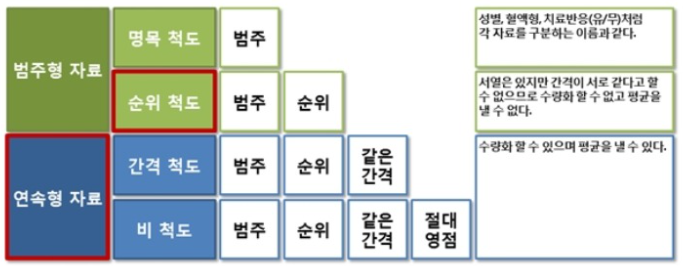
명목척도 예시) 성별(남자1, 여자2), 학년(1학년, 2학년, 3학년), 선수번호(9번, 10번, 11번) 등
순위척도 예시) 시험 성적 순위(1위,2위,3위), 키 순서(183cm, 177cm, 170cm)
간격척도 예시) 온도계(-10,0,10도), 월드컵 연도(1998,2002,2006)
비율척도 예시) 숫자로 표현되고, 영점 있는 자료 다 가능
위의 데이터들을 분석하는 방법 - 상관관계 분석, 회귀분석
상관관계분석은 정비례, 반비례 정도
회귀분석은 모델이 많음
2. 가설 수립
회귀 모델: 어떤 자료에 대해서 그 값에 영향을 주는 조건을 고려하여 구한 평균
회귀 분석: 평균을 구하는 함수 h()라 할 때, 이 h() 함수를 찾는 과정
사용 목표: 최대한 실제 h()에 가깝게 회귀 모델을 만들어서 어떤 작업의 과정을 딥러닝 시키는 것
데이터가 가진 특징이나 모델링 목적 등에 따라 적절한 회귀 모델을 사용하는 것이 중요하기 때문에 다양한 회귀 분석 기법을 알아 두는 것은 중요, 완벽한 모델 만드는 것은 불가능, 우리가 수행하려는 작업에 사용해도 괜찮은 정도의 모델을 만드는게 목표
회귀모델 종류
-
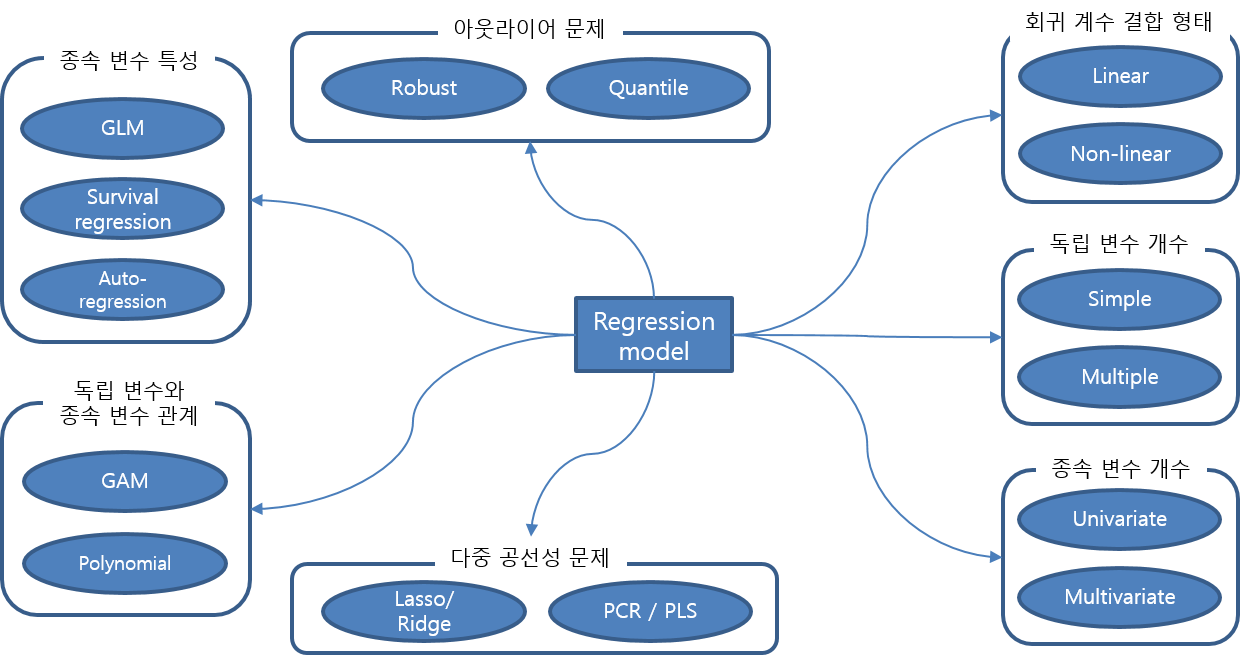
회귀 모델 특징에 따라 분류
-
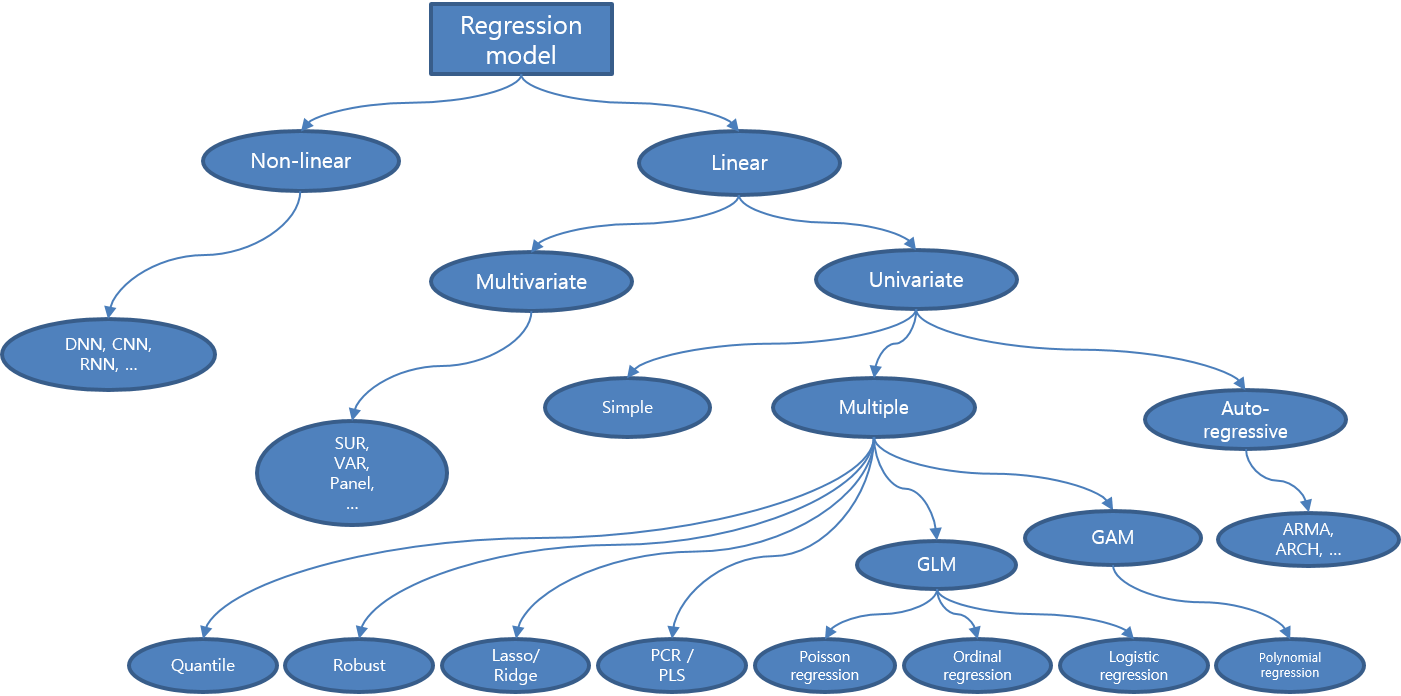
회귀 모델 계층구조
-
회귀 모델링 기준
- 선형성 / 비선형성 : 모델을 회귀 계수의 선형 결합만으로 표현할 것인지 결정
- 단변량 / 다변량 : 종속 변수 개수에 따라 결정
다변량은 패스, 단변량에 대해서 - 단순 / 다중 : 독립 변수 개수에 따라 결정
독립 변수와 종속 변수가 선형 관계가 아닌 경우: Polynomial regression, Generalized Additive Model (GAM)
오차항의 확률분포가 정규분포가 아닌 경우: Generalized Linear Model (GLM)
오차항에 자기 상관성이 있는 경우: Auto-regression
데이터에 아웃라이어가 있는 경우: Robust regression, Quantile regression
독립변수 간에 상관성이 있는 경우(다중공선성): Ridge regression, Lasso regression, Elastic Net regression, Principal Component Regression (PCR), Partial Least Square (PLS) regression
각 자세한 설명은 아래 링크
출처: https://danbi-ncsoft.github.io/study/2018/05/04/study-regression_model_summary.html
3. 비용함수 계산
비용함수 : 예측한 값과 실제 결과 값의 차이를 나타내는 함수, loss라고도 함, cost 최솟값 나오는 hx가 젤 좋은 가설
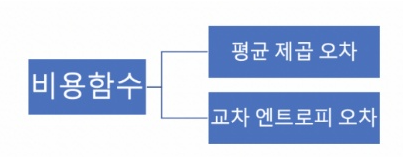
linear regression 경우) cost func (평균 제곱 오차)
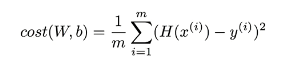
~ 경우) cost func (교차엔트로피 오차)
여기서 y_k는 소프트맥스 함수, 원 핫 인코딩으로 정답 표시

logistic regression 경우) cost func (이진 교차엔트로피 오차)
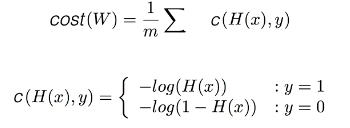
4. 경사하강법
경사하강법(GD, Gradient Descent)은 대표적인 optimizer임
- optimizer의 계보
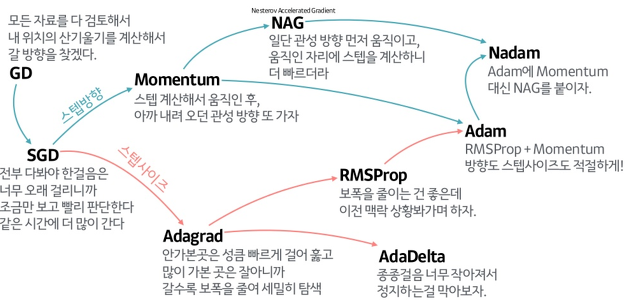
optimizer 역할?
activation func - reLU?
