이제서야 코딩테스트 준비를 하고 있는데 Heap문제만 나오면 벌벌 떨고 있어서 이번기회에 한번 제대로 파악을 해보기로 하였다! 또한 우선순위 큐에 대해서도 자세하게 파악을 해보고 갈려고 한다!
트리란?
- 비선형 계층적 자료구조?
- 재귀적 자료구조
- 하나의 루트 노드와 0개 이상의 하위 트리
- 단순 순환을 가지지 않고 연결된 무방향 그래프 구조
트리용어
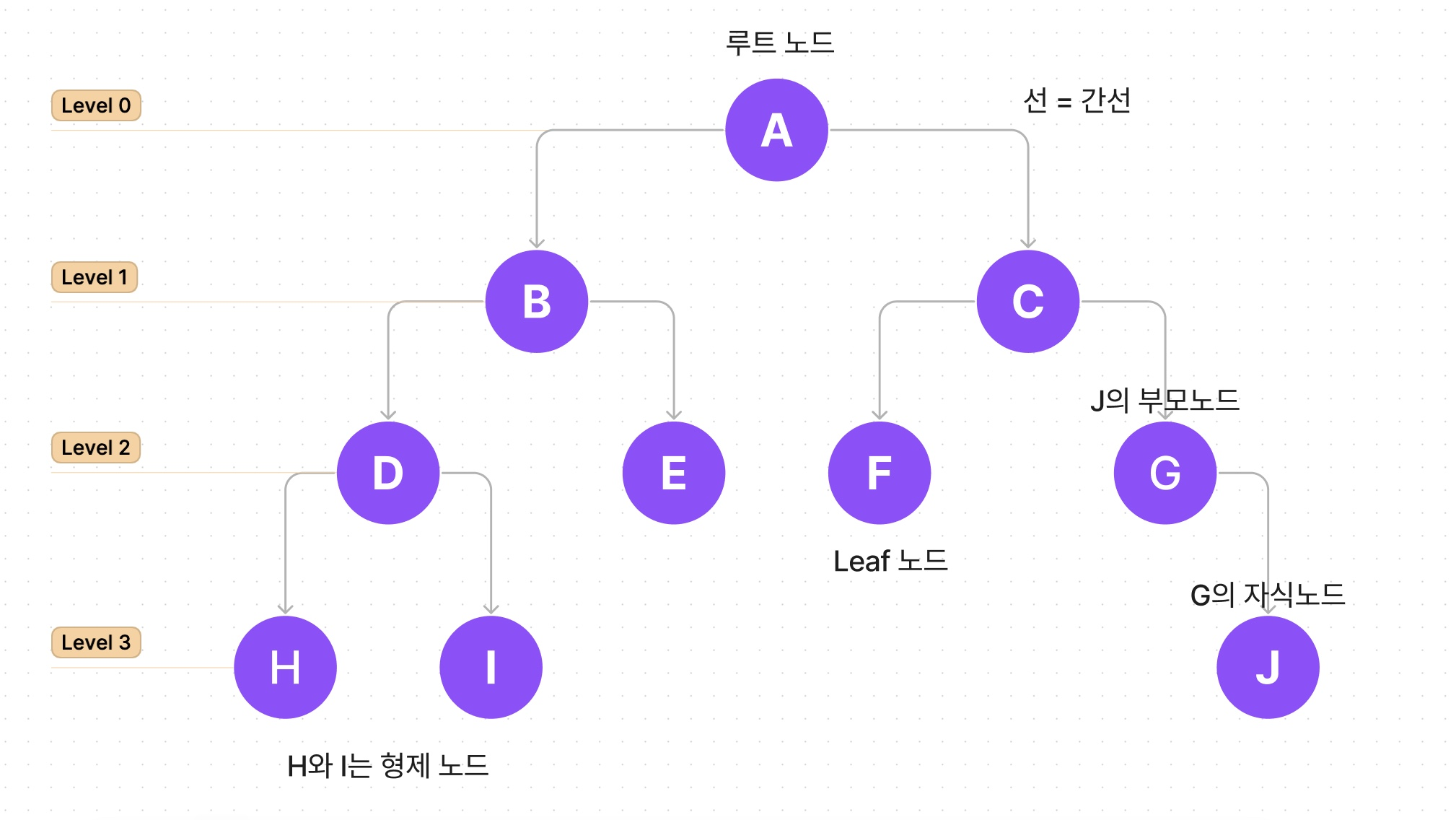
트리의 종류
이진트리
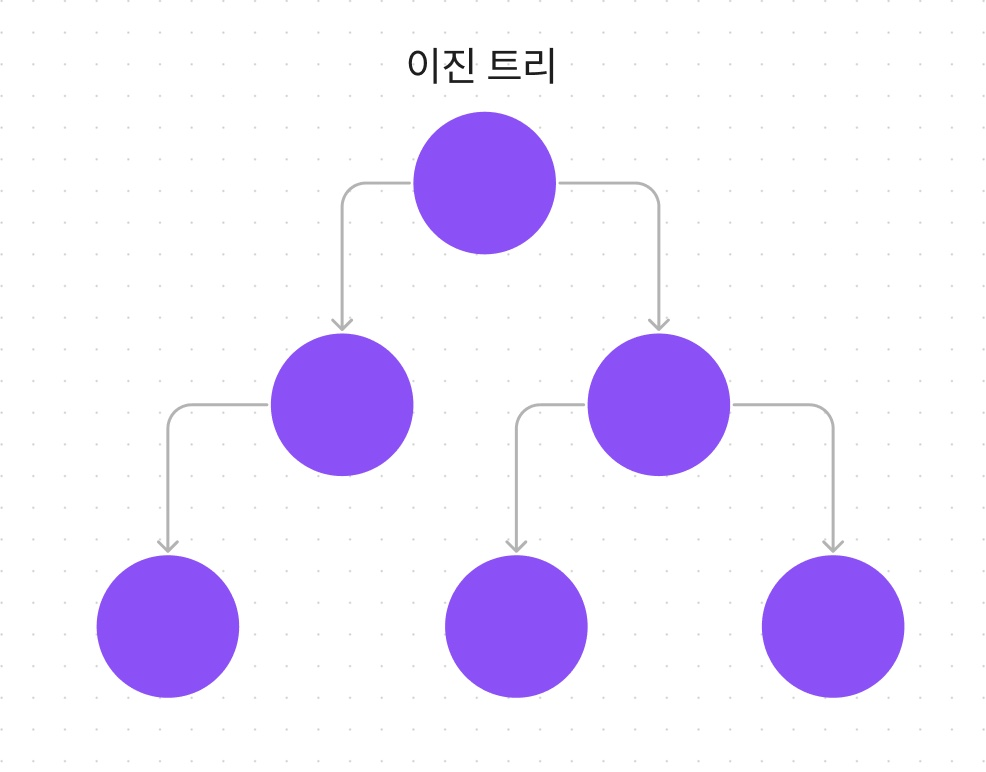
자식 노드가 최대 2개까지만 허용하는 트리
모든 트리가 이진트리는 아닙니다.
완전 이진트리
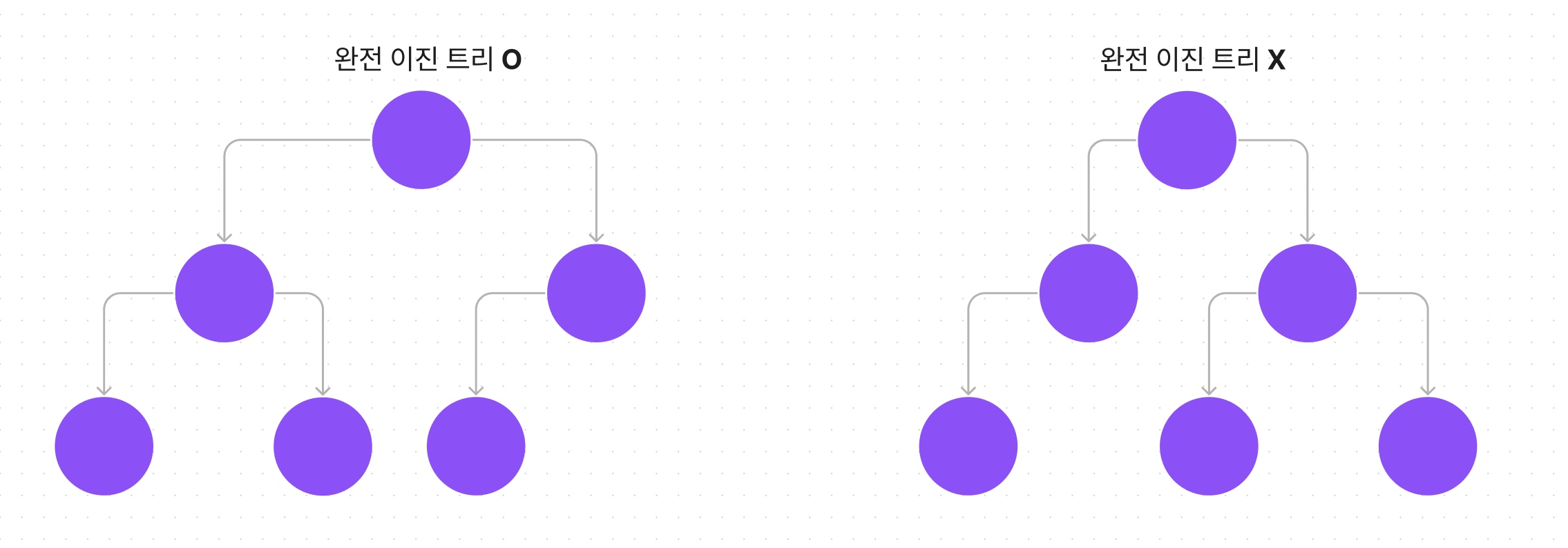
마지막 레벨을 제외한 모든 노드는 완전히 채워져 있어야 하며, 왼쪽에서 오른쪽으로 순서대로 차곡차곡 채워져있는 이진 트리
포화 이진 트리
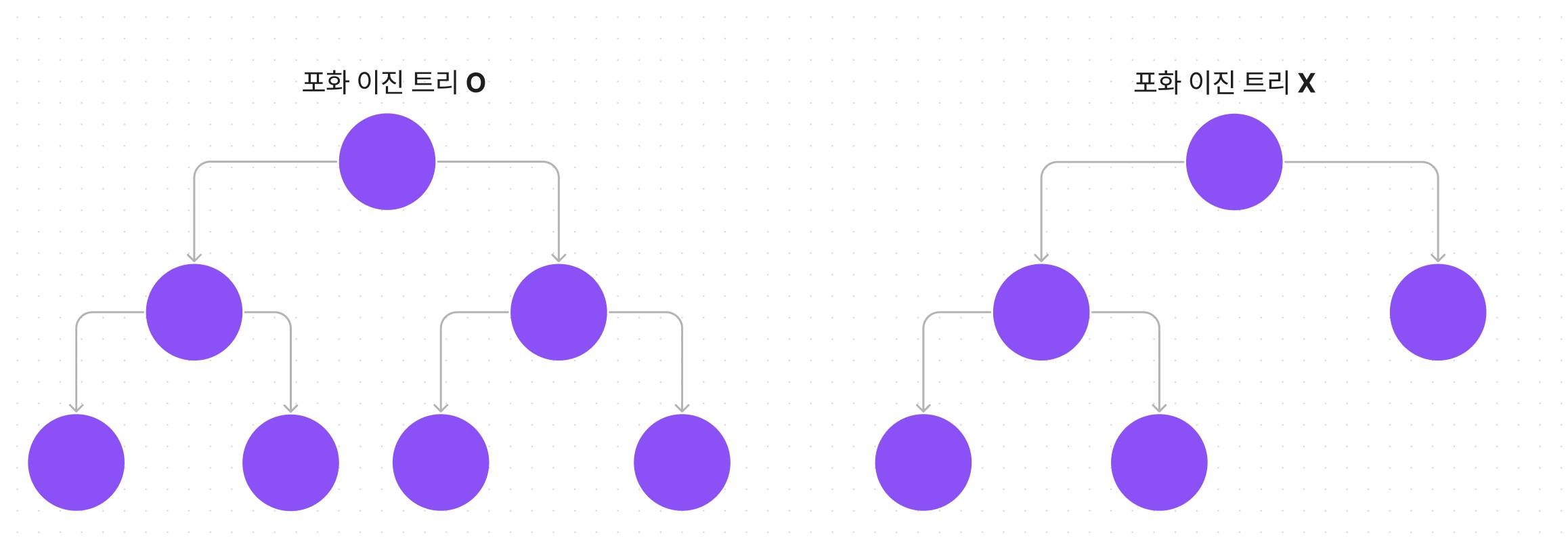
모든 노드의 차수가 2이며 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 이진트리
전 이진 트리
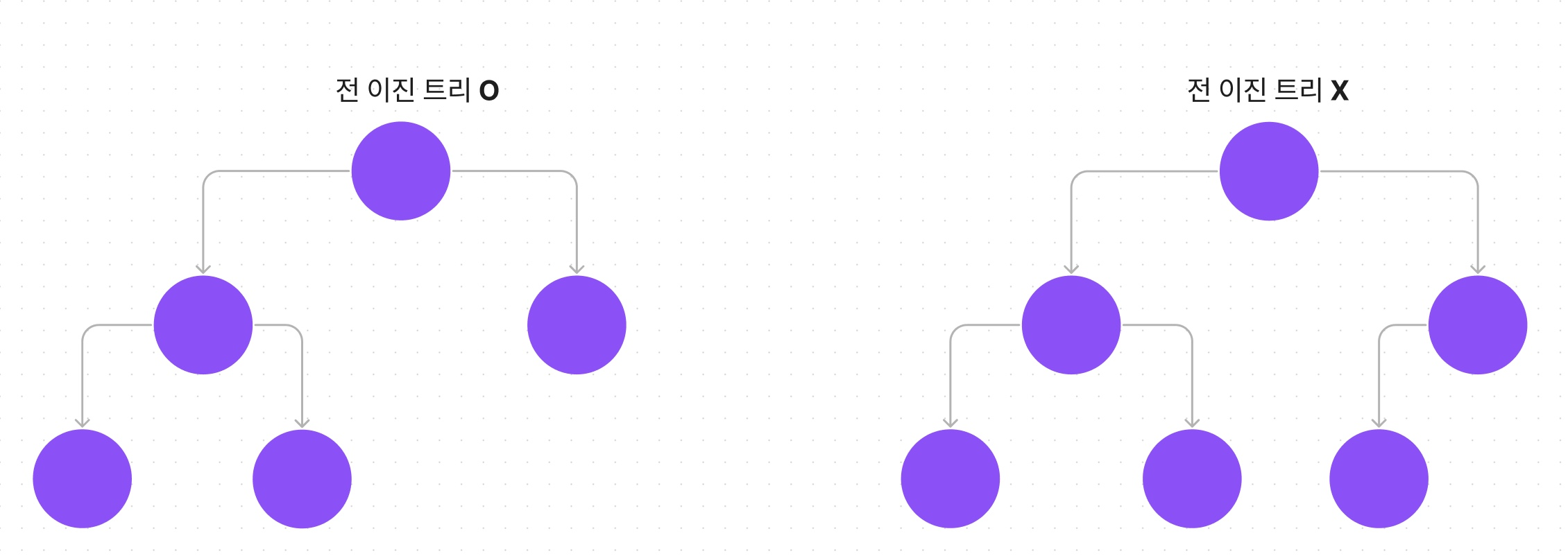
모든 노드의 차수가 2 혹은 0인 이진 트리
Heap이란?
- 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다!
- 여러개의 값들 중에서 최대값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다
- 힙은 반정렬 상태를 유지한다 => 큰값이 위에, 작은값이 아래에 있다!(Max heap)
- 힙트리는 중복된 값을 허용(이진 트리는 허용하지 않는다)
Heap의 종류
-
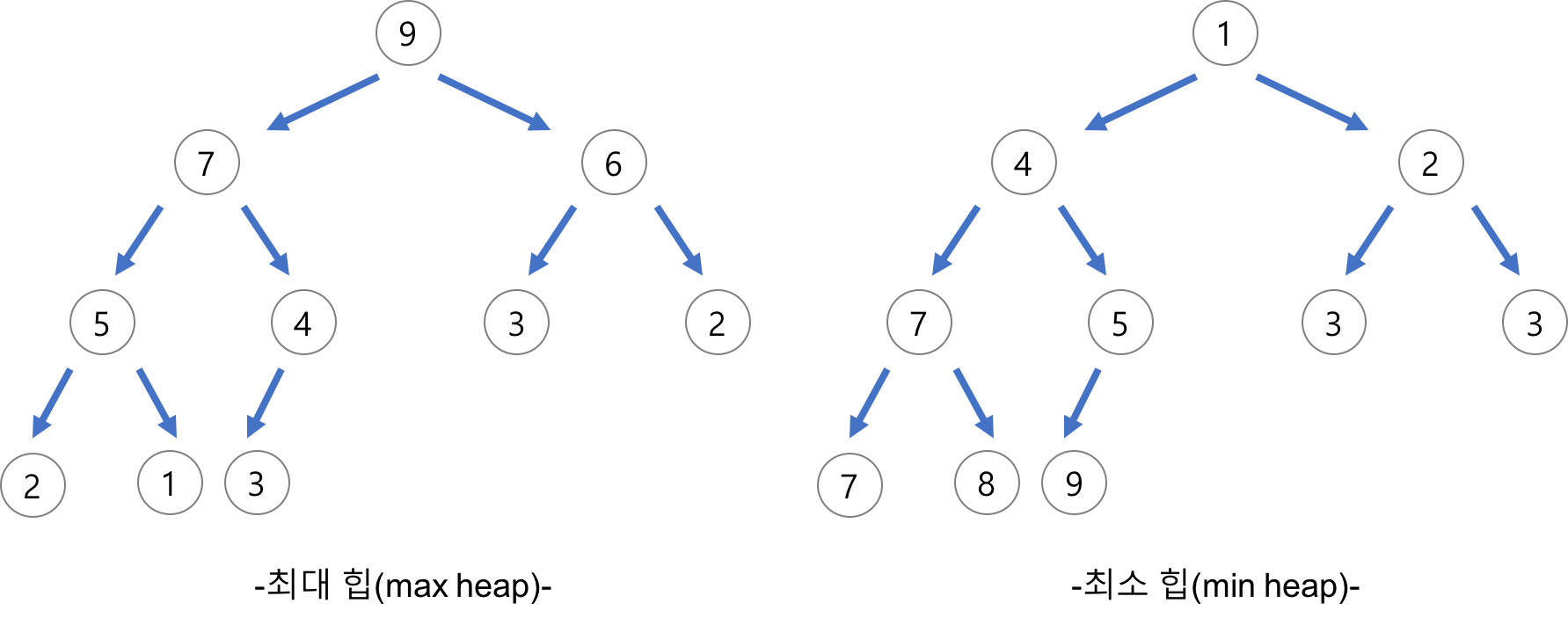
Max Heap
- 부모노드의 키 값 >= 자식노드의 키 값
-
Min Heap
- 부모 노드의 키 값 <= 자식노드의 키 값
Heap의 구현
- 배열로 만든다
- 첫번째 인덱스인 0을 사용하지 않고 만든다
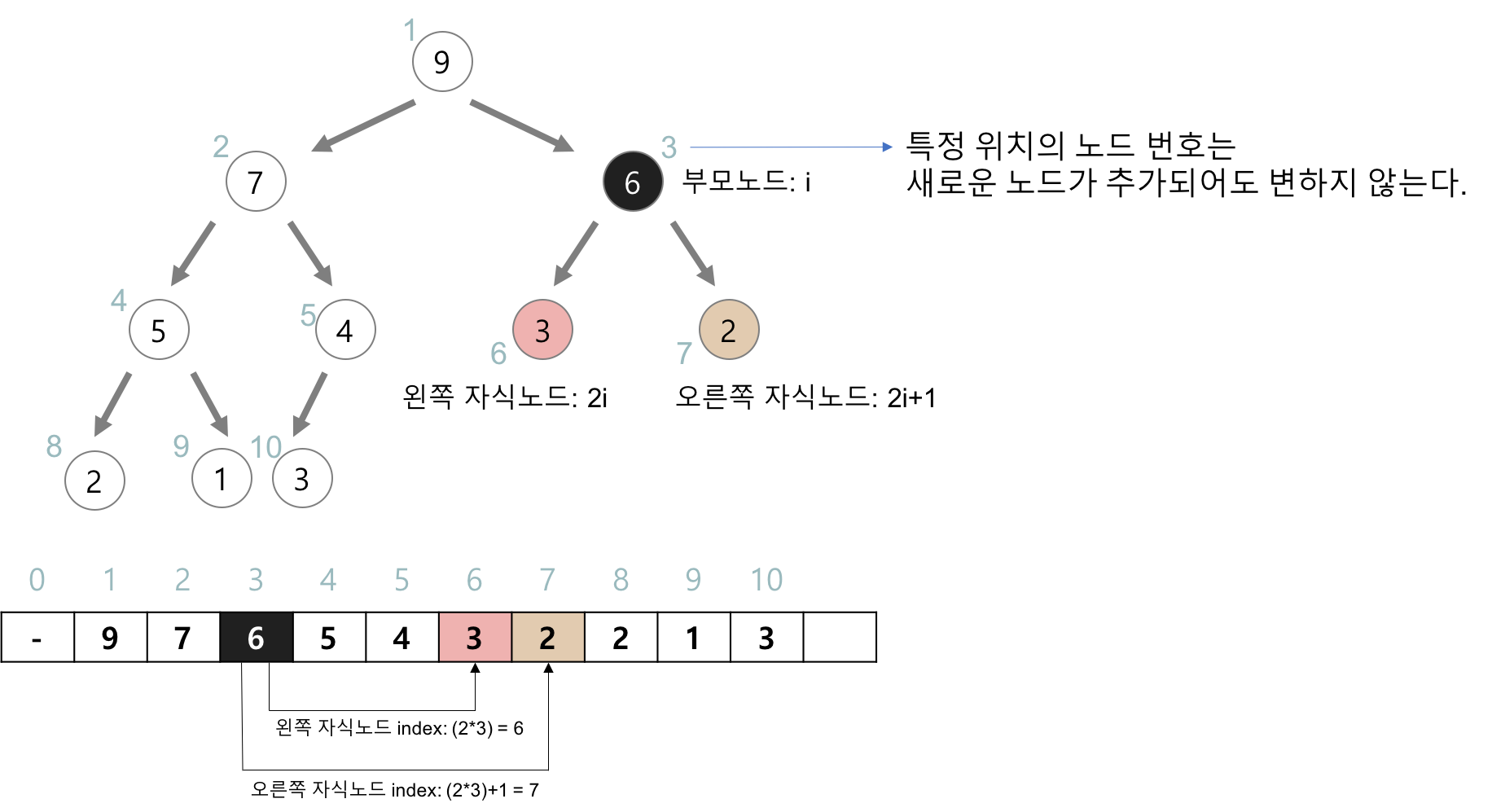
- 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다
인덱스 계산 공식
현재 노드 번호를 i라 할때,
◾ 현재 노드의 perent node의 번호 = (i - 1) / 2
◾ 현재 노드의 left child node의 번호 = i 2 + 1
◾ 현재 노드의 right child node의 번호 = i 2 + 2
(Root node가 0번일 경우 기준)
Python에서 Heap Queue알고리즘을 어떻게 사용하는가?
import heapq
min_heap = []
for i in range(N):
for number in map(int, sys.stdin.readline().strip().split()):
if len(min_heap) < N:
heapq.heappush(min_heap, number) # N개 미만일 때는 바로 추가
elif number > min_heap[0]:
heapq.heappushpop(min_heap, number) # N개를 넘으면 최솟값을 교체하여 N번째 큰 수 유지- heapq.heappush(heap, item)
- item을 힙에 추가하면서 힙 속성을 유지합니다.
- 힙에 새로운 요소를 추가할 때 사용합니다.
- heapq.heappop(heap)
- 힙에서 가장 작은 항목을 제거하고 반환하며, 힙 속성을 유지합니다.
- 만약 힙이 비어 있다면 IndexError가 발생합니다.
- 가장 작은 항목을 확인만 하려면 heap[0]을 사용할 수 있습니다.
- heapq.heappushpop(heap, item)
- item을 힙에 추가한 후, 힙에서 가장 작은 항목을 제거하고 반환합니다.
- heappush() 후 바로 heappop()을 호출하는 것보다 효율적입니다.
- heapq.heapify(x)
- 리스트 x를 힙으로 변환합니다.
- 이 작업은 제자리에서 수행되며, 선형 시간이 걸립니다.
- heapq.heapreplace(heap, item)
- 힙에서 가장 작은 항목을 제거하고 반환한 후, 새로운 item을 힙에 추가합니다.
- 힙의 크기는 변하지 않습니다.
- 힙이 비어 있을 때는 IndexError가 발생합니다.
- heappop() 후 heappush()을 사용하는 것보다 효율적이며, 고정 크기의 힙을 사용할 때 적합합니다.
- 이 함수는 item이 추가된 값보다 더 큰 값이 반환될 수 있습니다. 이 점이 원치 않는 경우, heappushpop()을 고려하세요. heappushpop()은 두 값 중 더 작은 값을 반환하고, 더 큰 값을 힙에 남깁니다.
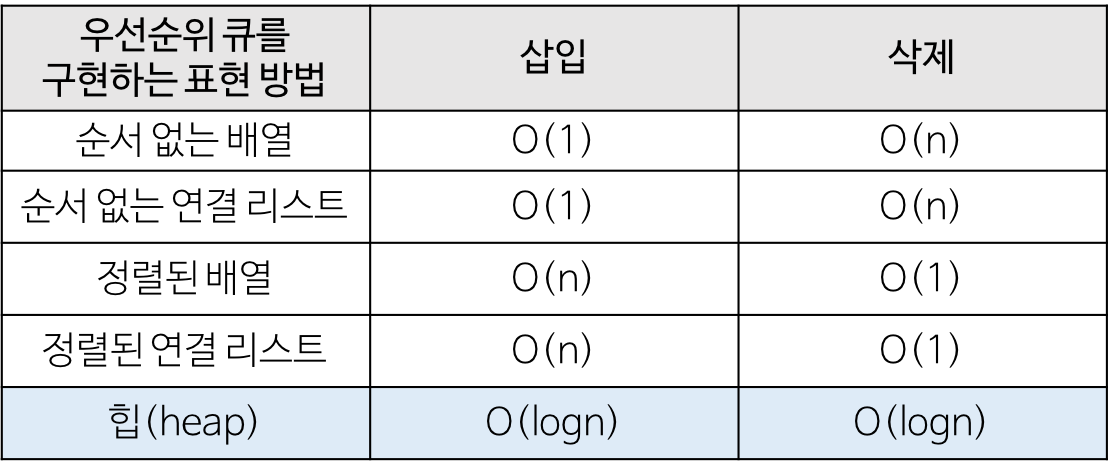
시간복잡도
- 자료를 추가하는 시간복잡도
- 루트 노드와 비교하는 상황이 최악: O(logN) - 자료의 삭제
- 맨위의 Root노드를 삭제하는 경우밖에 없다. 하지만 그러고 다시 형태를 갖추어야한다- O(logN)
우선순위 큐
- 우선순위의 개념을 큐에 도입한 자료구조
: 우선순위를 가지고 있고 우선순위가 높은 데이터가 먼저 나간다