[Algorithm] 트리 - Python

Sunwu Park·2024년 11월 17일
트리
0

Algorithm

목록 보기
12/12

서론

난 원래 이런 자료구조에 좀 약했는데 특히 트리 문제에서 약점을 보이고 있었다. 고로 이제 슬 취준을 해야할 시기가 왔기 때문에 더는 미루지 말고 트리 문제에 대해서 완전 정복을 해보기로 하였다

트리란?

  • 정의: 계층구조로 이루어진 노드와 간선의 집합이다

여기서 중요한것은 부모-자식 관계를 모두 포함하고 있다는 것이다

코딩테스트에서 트리 유형

1. 계층 구조를 이용하는 트리

  • 특징: 계층적 구조를 활용한 문제로, 부모-자식 관계를 정의하고 이를 기반으로 문제를 풀이.
  • 활용: 조직도, 디렉터리 구조 등.

2. 이진 탐색 트리(Binary Search Tree, BST)

  • 특징: 트리의 각 노드가 특정 규칙을 따름.
    왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드.
  • 활용: 빠른 검색, 삽입, 삭제 문제, 특정 값 검색, 범위 내 값 개수 구하기
  • Insert 과정
    1. Root에서 시작
    2. 삽입 값을 루트와 비교. 루트보다 작으면 왼쪽으로 재귀하고 크다면 오른쪽으로 재귀
    3. 리프 노드에 도달한 후 노드보다 크다면 오른쪽에 작다면 왼쪽에 삽입

3. 완전 이진 트리

  • 특징: 마지막 레벨을 제외한 모든 레벨이 꽉 차 있고, 마지막 레벨은 왼쪽부터 채워짐.
    - 어느 노드에 오른쪽 자식이 존재한다면 왼쪽 자식도 가지고 있어야 완전이진트리
  • 활용: 힙(Heap) 구현, 정렬 문제.

4. 최소 스패닝 트리 (Minimum Spanning Tree, MST)

  • 특징: 그래프에서 모든 노드를 연결하며 간선 가중치의 합이 최소인 트리를 구성.
    - 모든 정점들이 연결 되어 있어야 하고 사이클을 포함해서는 안된다.
  • 알고리즘:
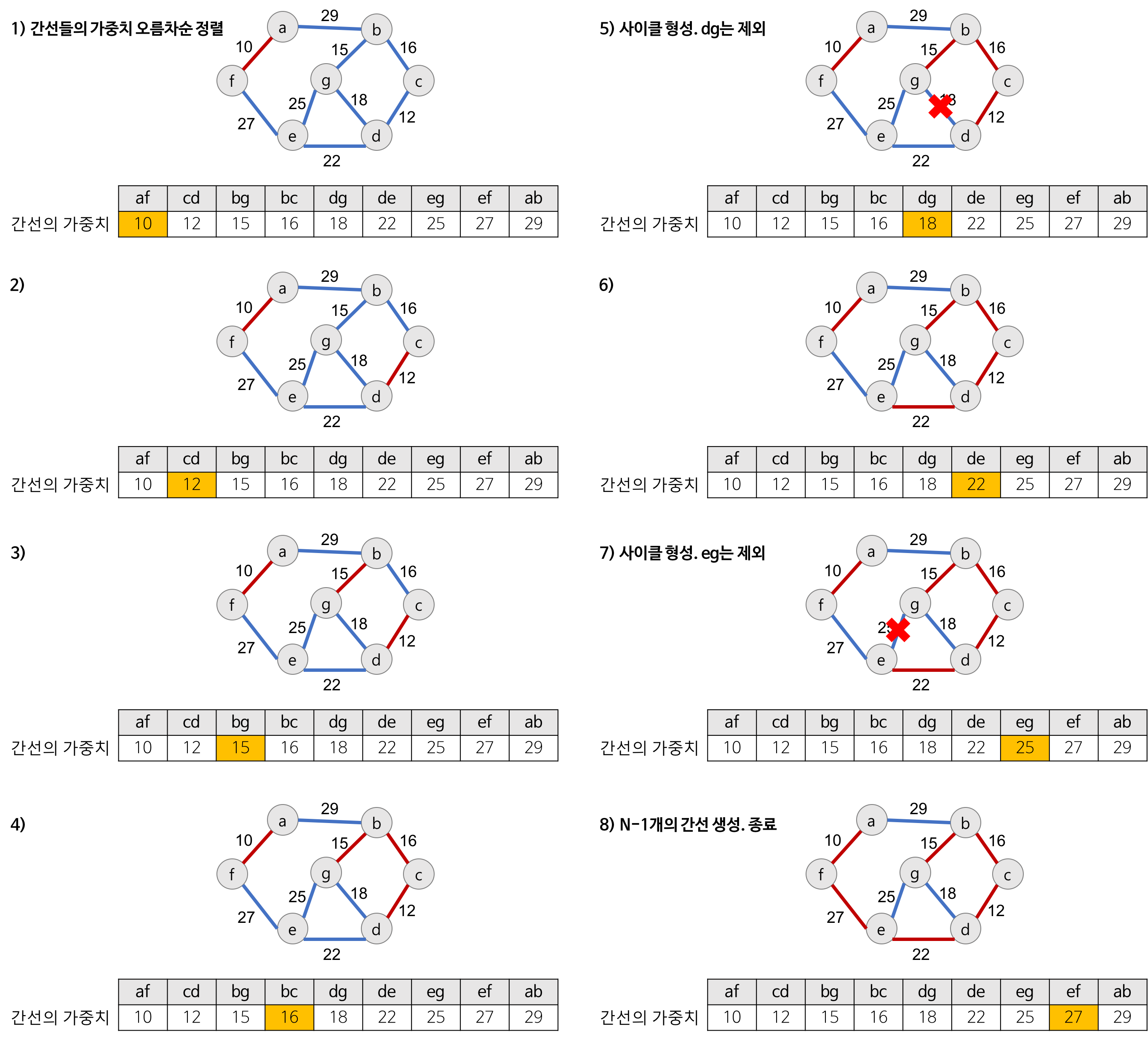
    - 크루스칼 알고리즘: 간선을 정렬 후, 유니온 파인드(Union-Find)로 트리를 구성.
    과정
    1. 그래프의 간선들을 가중치의 오름차순 정렬
    2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선 선택(낮은 가중치)
    3. 간선을 MST의 집합에 추가
# 특정 원소가 속한 집합을 찾기
def find(parent, x):
    if parent[x] == x:
        return x
    parent[x] = find(parent, parent[x])
    return parent[x]


# 두 원소가 속한 집합을 합치기 (간선 연결한다고 생각!)
def union(parent, a, b):
    rootA = find(parent, a)
    rootB = find(parent, b)

    if rootA < rootB:
        parent[rootB] = rootA
    else:
        parent[rootA] = rootB

for edge in edges:
    cost, a, b = edge
    # 사이클이 발생하지 않는 경우에만 집합에 포함(=연결한다.)
    if find(parent, a) != find(parent, b):
        union(parent, a, b)
        result += cost

크루스칼 알고리즘 출처 - kimdukbae 블로그

  • 프림 알고리즘: 시작 노드에서 간선을 하나씩 추가하며 최소 비용 트리를 구성.
    과정
    1. 시작 단계에서는 시작 정점만이 MST 집합에 포함
    2. 앞단계에서 만들어진 집합에 인접한 정점중 최소 간선 정점 선택하여 트리 확장
    3. 트리가 (N-1)개의 간선을 가질때까지 반복
      		```
      def mst():
      V, E = 6, 9
      edges = [[1, 2, 6], [1, 3, 3], [2, 3, 2], [2, 4, 5],
      [3, 4, 3], [3, 5, 4], [4, 5, 2], [4, 6, 3], [5, 6, 5]]
      graph = defaultdict(list)
      for srt, dst, weight in edges:
      graph[srt].append((dst, weight))
      graph[dst].append((srt, weight))
      mstgraph = [[0] * V for in range(V)]
      mstnodes = [-1 for in range(V)]
      visited = [True for _ in range(V)]
      q = [(0, 1, 1)]
      while q:
      cost, node, prev = heapq.heappop(q)
      if visited[node - 1] is False:
      continue
      visited[node - 1] = False
      mst_graph[node - 1][prev - 1] = 1
      mst_graph[prev - 1][node - 1] = 1
      mst_nodes[node - 1] = cost
      for dst, weight in graph[node]:
      if visited[dst - 1] is True:
      heapq.heappush(q, (weight, dst, node))
      print(f'MST cost is {sum(mst_nodes)}')
      mst_graph[0][0] = 1
      for row in mst_graph:
      print(*row)

프림 알고리즘 - 출처

  • 활용: 네트워크 연결, 최소 비용 경로 문제.

5. 트리의 지름 (가장 긴 경로)

  • 특징: 트리에서 가장 먼 두 노드 간의 거리.
  • 풀이 방법:
    1. 임의의 노드에서 DFS/BFS를 수행해 가장 먼 노드 A를 찾음.
    2. A에서 다시 DFS/BFS를 수행해 가장 먼 노드 B를 찾음.
    3. A와 B간의 거리가 트리의 지름.
  • 활용: 네트워크 최장 거리 문제.

6. 최소 공통 조상 (Lowest Common Ancestor, LCA)

  • 특징: 트리에서 두 노드의 가장 가까운 공통 조상을 찾음.
  • 풀이 방법:
    - DFS로 각 노드의 깊이를 맞춘 뒤 공통 조상을 탐색.
    - 희소 배열(Sparse Table)을 이용해 빠르게 탐색 (O(log N)).
  • 활용: 계층 구조 분석, 경로 탐색 문제.
def lca(a,b):
	## 무조건 a가 더 높은 정점이다
	if level[a] < level[b]:
    	swap(a,b)
    
    ## 정점이 같아질때까지 거슬러 올라간다
    while level[a] != level[b]:
    	a = parent[a]
        
    ## 정점이 같을때까지 거슬러 올라간다
    while a != b:
    	a = parent[a]
        b = parent[b]
    return a

7. 세그먼트 트리 및 펜윅 트리

  1. 세그먼트 트리:
  • 특징: 특정 구간에 대해 합, 최솟값/최댓값 등을 빠르게 계산.
  • 구현: 재귀적으로 구간을 분할해 트리 구조로 표현.
  1. 펜윅 트리 (Fenwick Tree):
  • 특징: 세그먼트 트리보다 구현이 간단하며, 배열을 기반으로 구간 연산을 수행.
  • 활용: 구간 합 문제, 업데이트 연산.

8. 트리 순회

  1. 전위 순회 (Preorder): 루트 -> 왼쪽 -> 오른쪽.
  2. 중위 순회 (Inorder): 왼쪽 -> 루트 -> 오른쪽.
  3. 후위 순회 (Postorder): 왼쪽 -> 오른쪽 -> 루트.

  • 활용: 트리의 특정 순서로 노드를 처리하는 문제 (예: 이진 검색 트리 재구성).

    class Node:
  def __init__(self, data, left_node, right_node):
      self.data = data
      self.left_node = left_node
      self.right_node = right_node

# 전위 순회(Preorder Traversal)
def pre_order(node):
    print(node.data, end=' ')
    if node.left_node != None:
        pre_order(tree[node.left_node])
    if node.right_node != None:
        pre_order(tree[node.right_node])

# 중위 순회(Inorder Tarversal)
def in_order(node):
    if node.left_node != None:
        in_order(tree[node.left_node])
    print(node.data, end=' ')
    if node.right_node != NOne:
        in_order(tree[node.right_node])

# 후위 순회(Postorder Traversal)
def post_order(node):
    if node.left_node != None:
        post_order(tree[node.left_node])
    if node.right_node != None:
        post_order(tree[node.right_node])
    print(node.data, end=' ')

유형 활용 예제
1. 계층 구조 트리: 조직도, 디렉터리 구조, 부모-자식 관계
2. 이진 탐색 트리: 빠른 값 검색, 범위 쿼리 문제
3. 완전 이진 트리: 힙 구현, 정렬 문제
4. 최소 스패닝 트리: 네트워크 최소 비용 연결 문제
5. 트리의 지름: 네트워크 최장 거리 문제
6. 최소 공통 조상: 공통 관리자 찾기, 경로 계산 문제
7. 세그먼트/펜윅 트리: 구간 합/최솟값/최댓값 문제
8. 트리 순회: 트리 변환, 특정 노드 처리 순서 문제

백준 문제 풀기

트리 - 1068 (GOLD V)

트리에서 리프 노드란, 자식의 개수가 0인 노드를 말한다.

트리가 주어졌을 때, 노드 하나를 지울 것이다. 그 때, 남은 트리에서 리프 노드의 개수를 구하는 프로그램을 작성하시오. 노드를 지우면 그 노드와 노드의 모든 자손이 트리에서 제거된다.

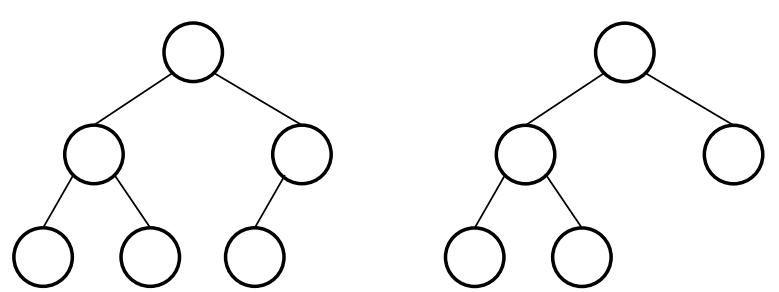
예를 들어, 다음과 같은 트리가 있다고 하자.

현재 리프 노드의 개수는 3개이다. (초록색 색칠된 노드) 이때, 1번을 지우면, 다음과 같이 변한다. 검정색으로 색칠된 노드가 트리에서 제거된 노드이다.

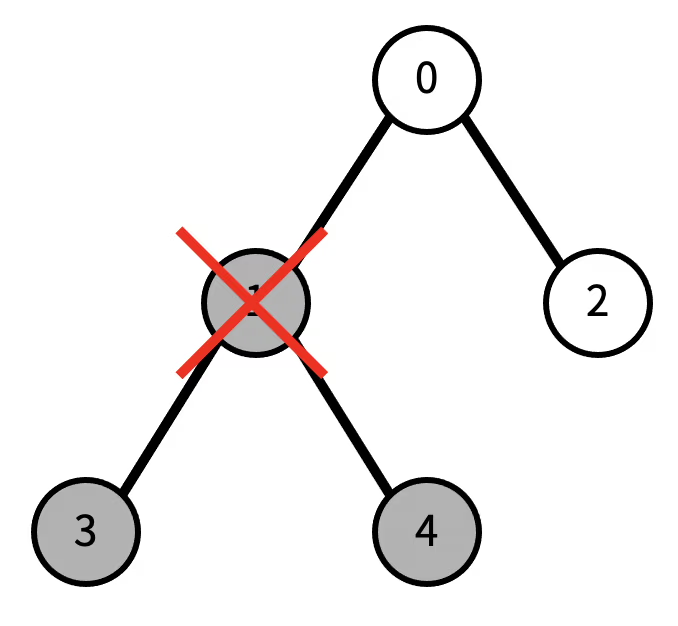
이제 리프 노드의 개수는 1개이다.

입력

첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다. 셋째 줄에는 지울 노드의 번호가 주어진다.

출력

첫째 줄에 입력으로 주어진 트리에서 입력으로 주어진 노드를 지웠을 때, 리프 노드의 개수를 출력한다.

풀이 과정

당연히 그 부모 트리밑으로만 없애면 된다고 해서 그 밑부터는 DFS로 삭제해서 해결하면 된다고 생각을 하였다. 하지만 그 노드도 삭제되어 그 위의 부모 노드도 신경을 써야하였고 또한 카운트를 하는것은 Leaf노드고 입력으로 들어오는 것은 부모노드이기때문에 부모노드가 아니면서 -2도 아닌것을 찾으면 된다!

코드

import sys
input = sys.stdin.readline

def dfs(num, arr):
    arr[num] = -2
    for i in range(len(arr)):
        if num == arr[i]:
            dfs(i, arr)

n = int(input())
arr = list(map(int, input().split()))
k = int(input())
count = 0

dfs(k, arr)
count = 0
for i in range(len(arr)):
    if arr[i] != -2 and i not in arr:
        count += 1
print(count)
profile
Sunwu Park
이전 포스트

[Algorithm] Heap & Priority Queue

0개의 댓글